움짤로 익히는 스도쿠 22. 데스 블라썸(Death Blossom)

 최근에 ALS라는 공식을 알게 된 후로 XY체인과, XY윙, XYZ윙, WXYZ윙이 잘 보여지게 되고 있다. ALS공식 자체는 2개의 연속된 ALS 2개의 세트가 있는 경우에 적용는데, 데스 블라썸은 좀 더 확장된 개념으로 연결되지 않은 ALS 2개의 세트를 피벗 기능을 하는 칸이 연결 시키는 확장된 ALS라고 보면 되겠다. 아무리 뜯어봐도 왜 명칭이 데스 블라썸인지 모르겠다. (발견자의 마음인 듯.. 하다)

 

 경우에 따라서는 3개의 ALS 세트가 연결된다고 보면 되지만 아직 검증이 되지 않아서 2개의 세트를 피벗으로 연결한다.. 는 개념으로 보는 게 맞을 듯 하다. 

 

 개념 자체는 어렵지 않지만 눈에 잘 띄지 않아서 저 세상 공식에 올린다. 

 

 만약에 ALS 개념을 몰라도 이해하는데는 무리는 없다고 생각하지만 그래도 좀 더 기본이 되는 ALS를 아래 링크에서 보고 오면 좋겠다고 생각한다. 

 

움짤로 익히는 스도쿠 18. 거의 잠긴 세트(ALS)

움짤로 익히는 스도쿠 18. 거의 잠긴 세트(ALS)

 

 자료를 찾아봐도 많지는 않다. 이번 글에서도 예제가 딱 2개뿐이다. 

 

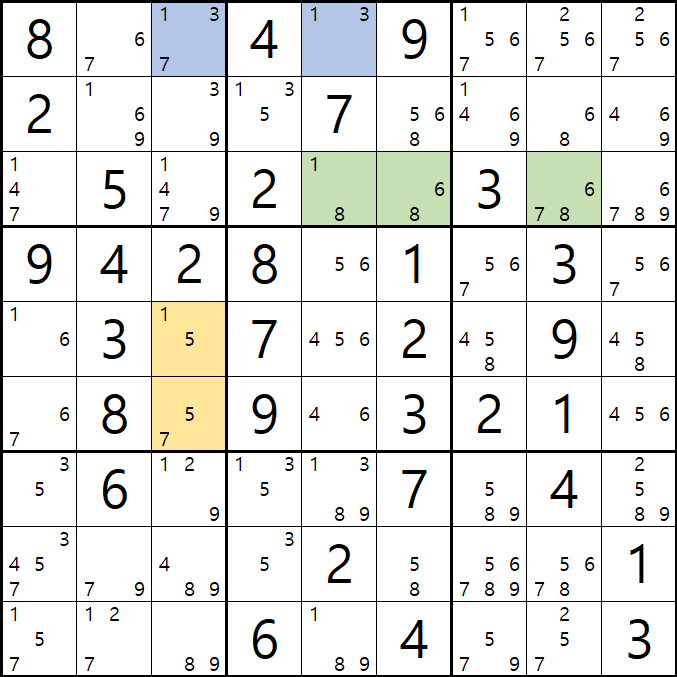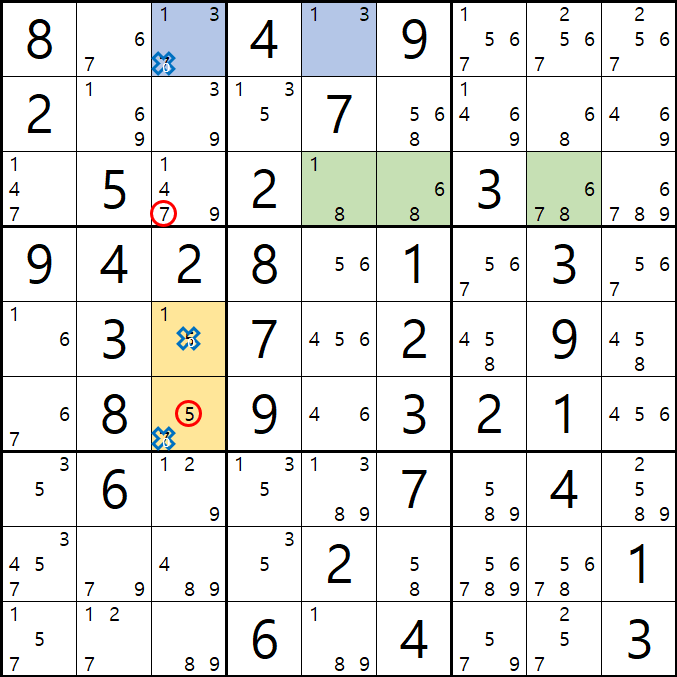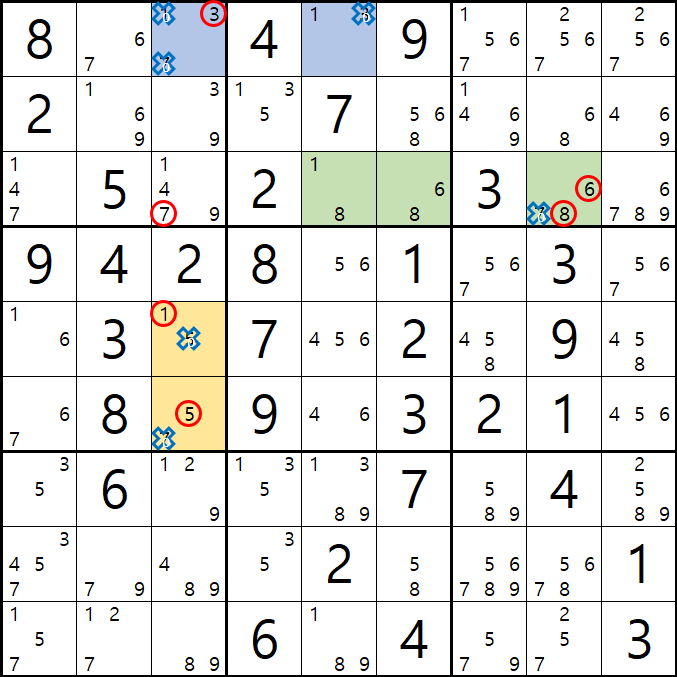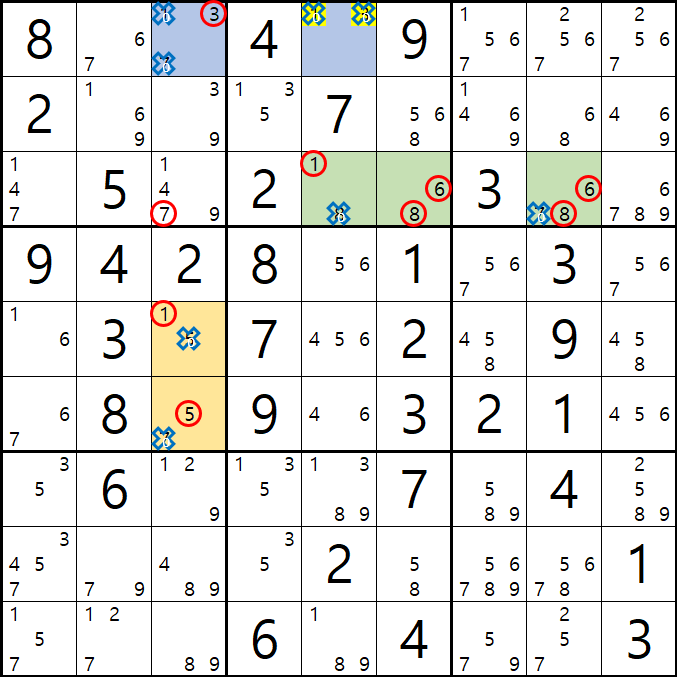
움짤예제1. 행과 열을 잇는 데스 블라썸 (ALS[3열 및 C행] + 피벗 A5)

 

 

1/3/5/7을 베이스로 하는 1번 ALS[A3, E3, F3]과 

1/6/7/8을 베이스로 하는 2번 ALS[C5, C6, C8]이 있을 때, 

 

1번과 2번 ALS를 피벗인 1/3[A5]이 

 

제한된 공통 후보숫자 3이 3[A3] > 3[A5] > 1[A5]로 연결되고 

비제한된 공통 후보숫자 1과 1[A5] > 1[C5]로 연결 될 때, 

 

피벗에 존재하는 후보숫자 1/3[A5]를 제외하고, 

1번과 2번 피벗의 공통 후보숫자 7[F3]과 7[C8]이

동시에 마주보는 후보숫자 7[C3]을 제거할 수 있다. 

 

위의 예제를 체인으로 정확히 설명할 수는 없지만 '...후보숫자 7[C3]을 제거할 수 있다.'는 결론을 역으로 추적하면 아래와 같이 증명이 가능하다. 

 

증명1. 움짤예제1. 증명 (좀 복잡하지만 이해하는데 어려움은 없다.)

 

+7[C3]이라면

+7[C3] -7[F3&A3] +5[F3] - 5[E3] +1[E3] +3[A3] -3[A5]가 되고

 

+7[C3] -7[C8]이 되면

6/8[C6]과 6/8[C8]이 확실한 페어가 되어 -8[C5] +1[C5] -1[A5]가 되므로 

 

A5칸에 동시에

-3[A5] -1[A5] 모든 숫자가 OFF가 되는 모순이 발생하기 때문에 

+7[C3]은 제거 되어야 한다. 

 

 

움짤예제2. 행과 열을 잇는 데스 블라썸 (ALS[D행 및 박스9] + 피벗 G3)

 

 

3/5/7을 베이스로 하는 1번 ALS[D3, D7]과 

2/3/6/8/9를 베이스로 하는 2번 ALS[G7, G8, G9, I9]가 있을 때, 

 

1번과 2번 ALS를 피벗인 6/7[G3]이 

 

제한된 공통 후보숫자 7이 7[G3] > 7[D3]로 연결되고 

비제한된 공통 후보숫자 6과 6[G3] > 6[G7, G8]로 연결 될 때, 

 

피벗에 존재하는 후보숫자 6/7[G3]을 제외하고, 

1번과 2번 피벗의 공통 후보숫자 3[D7]과 3[I9]이

동시에 마주보는 후보숫자 3[D9, E9, F9, I7] 4개의 후보숫자를 제거할 수 있다. 

 

증명2. 움짤예제2. 증명 (좀 복잡하지만 이해하는데 어려움은 없다.)

 

 

3[D9, E9, F9, I7] 이라면

+3[D9, E9, F9, I7] -3[D7] 이 되고

 

+3[D9, E9, F9, I7] -3[I9] 이 되면

2/8[I9]과 2/8[G9]이 확실한 페어가 되며서 -2[G7]이 되고,

6/9[G7]과 6/9[G8]이 확실한 페어가 되어 

-6[G3] +7[G3] -7[D3] +5[D3] -5[D7]가 되므로 

 

D7칸에 동시에

-5[D7] -3[D7] 모든 숫자가 OFF가 되는 모순이 발생하기 때문에 

+3[D9, E9, F9, I7] -3[D7]은 제거 되어야 한다. 

 

 나도 위에서 살펴 본 예제는 '스도쿠 위키'라는 곳에서 튜토리얼을 본 거라서 비슷한 사례 발견이 어려운 저 세상 레벨로 봤는데... ALS를 이루는 숫자를 이중값으만 한정하면 잘 보이는 것을 알게 됐다. 

 

위의 움짤은 3/4/8이 잠기는 XY윙인데 이 것을 ALS로 보면

 

 

위의 움짤처럼 ALS로 볼수 있고

 

이 것을 아래 움짤처럼 칸마다 ALS로 분리했다고 보면

A2의 후보숫자 3과 8이 각각 B3과 I2를 바라보며 연결해주는 데스 블라썸 형태가 된다. 이렇게 생각을 좀 더 확장해서 간단한 데스블라썸 부터 찾기 시작하면 나~~ 중에 처음에 설명한 삼중값의 데스 블라썸까지 가기 편해 질 것이다. 

 

물론 아래와 같이 XY체인으로 풀어낼 수도 있다.