움짤로 익히는 스도쿠 18. 거의 잠긴 세트(ALS)

 이번 글에서는 Almost Locked Sets라고 불리는 저 세상 공식들에 준하는 고급으로 바꾼다. 이해하고 찾다보면 세상 쉽고 유용한 공식이 되겠다. 다만 찾기가 쉽지 않다. 또한 다른 페이지를 빌어서 증명해 보겠지만 XY 체인을 찾는데도 매우 좋은 공식이다. 그리고 단일 숫자로 연결되는 체인 외에 2개 이상이 결합되는 체인에서는 근본이라고 생각한다. 

 

 ALS에 대해 알아보도록 하겠다. 명칭에서 알 수 있듯이 거의 잠긴 세트 또는 준 잠긴 세트 정도로 보면 되겠다. 글로만 설명하면 어려우니 움짤 예제를 보면서 개념을 바로 익혀나가도록 하자. 2개의 규칙이 있는데 RULE1(고급 공식), RULE2(준 저세상 공식)라고 구분하겠다.

 

예제는 칸의 ALS를 열결하는 칸의 후보숫자가 2개 + 3개 이렇게 나가는데, 

 

처음에는 모든 칸에 후보숫자가 2개 있는 이중값만 찾고 (W윙, XY윙과 XY체인 및 AIC 체인에도 적용 가능하다.)

고급으로 가면 칸에 2~3개의 숫자가 조합된 스트롱 + 위크 링크를 찾으면 좋다고 생각한다.  

 

자 바로 움짤 예제로 출발이다. 

 

1. ALS RULE1-1탄. (2+2)

 

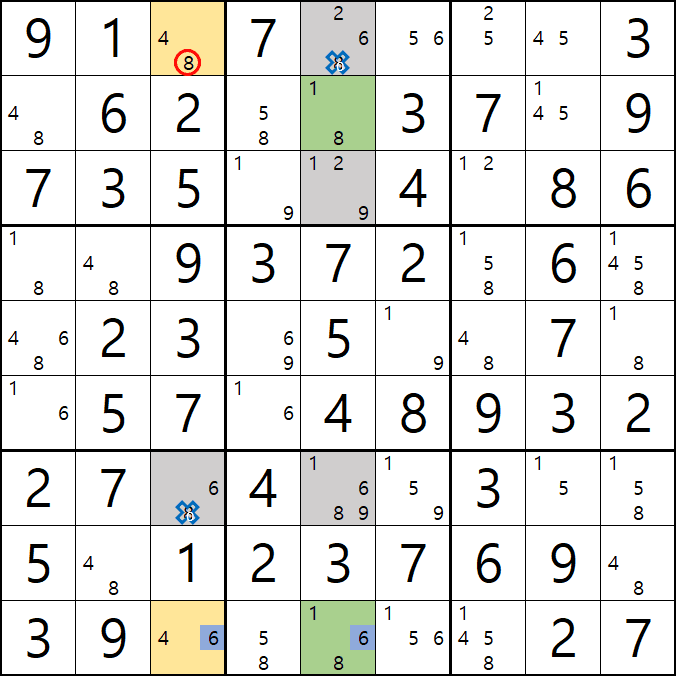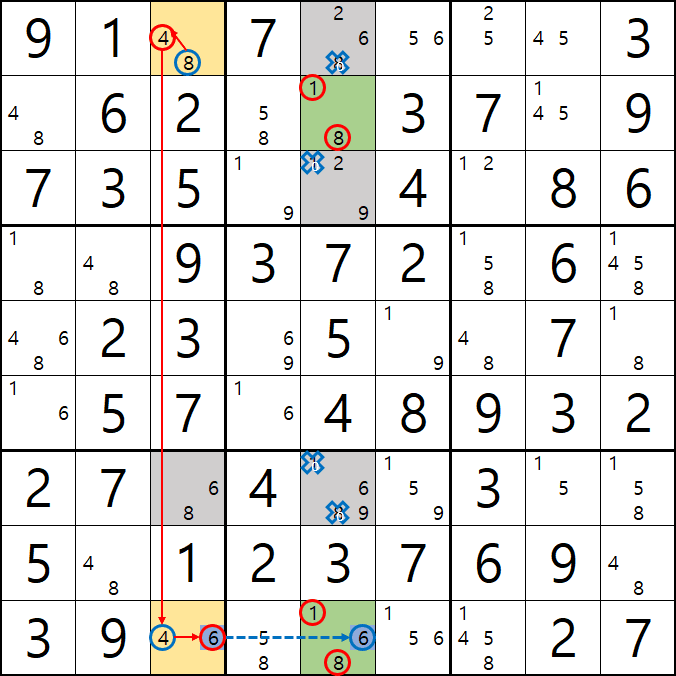
1-1. 위의 움짤 처럼 3열에 '확실한 트리플'인 4/8[A3], 6/8[G3], 4/6[I3] 완벽하게 잠긴 세트가 존재 하는데 

이 중에서 노란색으로 칠한 4/8[A3], 4/6[I3] 2개만 취하면

4/6/8 확실한 트리플을 이루다 만 불완전한 '거의 잠긴 세트'가 된다. 

 

1-2. 또한 5열에는 1/2/6/8/9로 조합된 확실한 퀸 2/6/8[A5], 1/8[B5], 1/2/9[C5], 1/6/8/9[G5], 1/6/8[I5] 이 존재 하는데

이 중에서 초록색으로 칠한 1/8[B5], 1/6/8[I5] 만 취하면 1/6/8 트리플을 이루는 불완전한 '거의 잠긴 세트'가 된다. 

 

1-3. 즉, 확실한 트리플은 3칸 (XYZ의 조합) 으로 이뤄지는데, 2칸 이하로 존재하면 '준 잠긴 세트'[ 즉, 최소한 (잠긴 세트 - 1~2칸) ]라고 보면 되고ALS에서는 이 거의 잠긴 세트 2세트를 조합했을 때 발생하는 조건으로 다른 칸의 후보수를 제거하는 공식이다. 

 

1-1에서 칠한  4/8[A3], 4/6[I3]과 1-2에서 칠한 1/8[B5], 1/6/8[I5] 2개의 '거의 잠긴 세트'를 조합하면 임시로, 1/4/6/8의 확실한 쿼드러플을 이루는 것을 알 수 있다. 

 

 이렇게 2개의 잠긴 세트에서 1~3개의 후보숫자 조합만 빼낸 '거의 잠긴 세트'를 조합해서 임시로 새로운 잠긴세트로 만들어서 다른 칸의 후보숫자를 제거하는 공식을 Almost Locked Sets, ALS라고 부른다. 하지만 아직 중요한 것이 남았다.

 

1-4. 4개의 새로운 잠긴 세트 중에서 서로 공유되는 후보숫자는 

4/6[I3]과 1/6/8[I5]에 있는 후보숫자 6인 것을 알 수 있다. 

 

2개의 거의 잠긴 세트에서 유일하게 열결되는 숫자로 

이를 '제한된 공통 후보숫자'라고 부른다. 

 

 이 제한된 공통 후보숫자가 있기 때문에 4/8[A3], 4/6[I3] 과 1/8[B5], 1/6/8[I5] 2개의 '거의 잠긴 세트가' 새로운 하나의 잠긴 세트가 되는 것을 알 수 있다. 

 

(큭 나도 글을 쓰면서 문제를 까먹었다. 결과만 짤로 올리면...)

 

 

 1-5. 결론이다. 공통후보숫자인 6을 제외하고 나머지 후보숫자 전체가 바라보는 후보숫자를 지울 수 있는데

움짤예제 1에서는 8[A3]과 8[B5&I5(그룹링크 표현)] 이 동시에 바라보는 8[A5]를 제거할 수 있다. 

 

1-6. 이를 체인공식으로 증명해 보면 

 

증명1.  4/8[A3]이 8이라면 아래 움짤과 같이

 

8[A5], 8[G3] 2개의 후보숫자 8이 제거 되고 

 

증명2.  4/8[A3]이 8이 아니라면(즉, 4라면) 아래 움짤과 같이

 

-8[A3] +4[A3] -4[I3] +6[I3] -6[I5]가 되어

1/8[B5]와 1/8[I5]가 확실한 페어가 되어 

1[C5], 1[G5], 8[A5], 8[G5] 의 후보숫자 4개가 제거된다. 

 

 

증명3. 증명 1과 2에서 어떤 경우라도 제거되는 후보숫자는 8[A5]임을 알 수 있다. 

 

 

증명 4. 좀 더 직관적으로 증명을 하면

 

 

8[A5]가 되면

+1[B5] -8[G5] -8[I5] 및

+4[A3] +6[I3] +1[I5] 가 되어 

5열에 +1[B5] +1[I5] 동일한 후보숫자 2가 해가 되는 모순이 발생한다. 

이 모순을 제거하기 위해서는 8[A5]를 제거해야 한다. 

 

자 장황하게 떠들었지만 원리자체는 매우 간단하다. 

 

1. 2개의 하우스에 걸쳐 있는 '거의 잠긴 세트' 2개를 연결하는

2. 제한된 공통 후보숫자가 있는 새로운 잠긴 그룹을 찾는다.

3. 거의 잠긴 세트 2개에서 동시에 보는 숫자를 제거한다. 

 

끝'이다. 

 

자 예제를 계속 보면서 익히자. '언제까지?' '이해할 때 까지~'

 

2. ALS RULE1-2탄. (1+3)

 

 

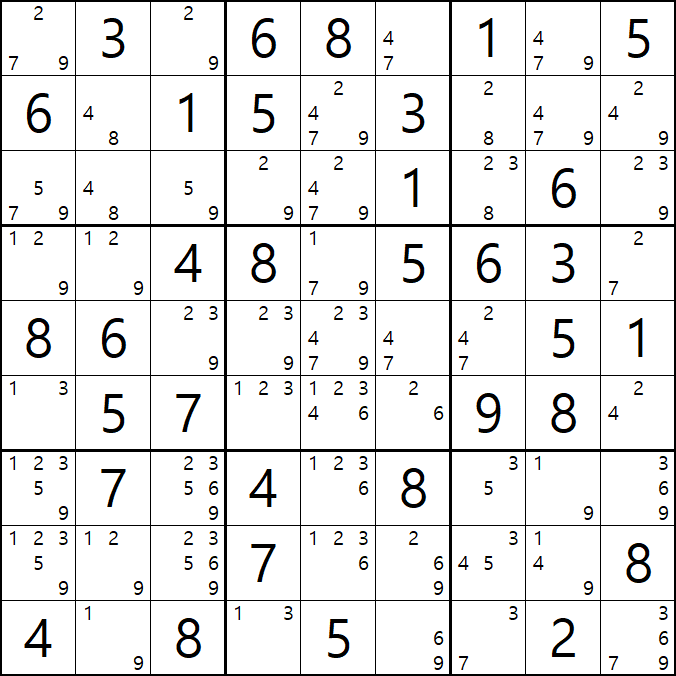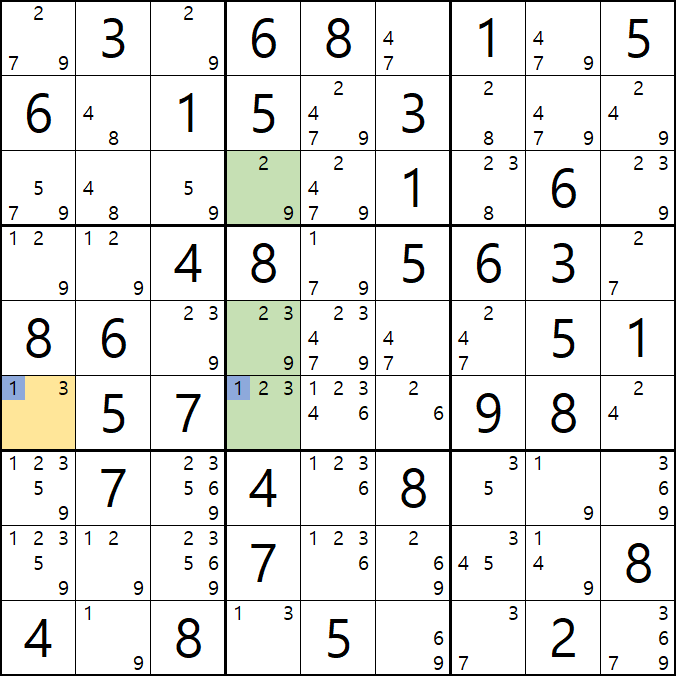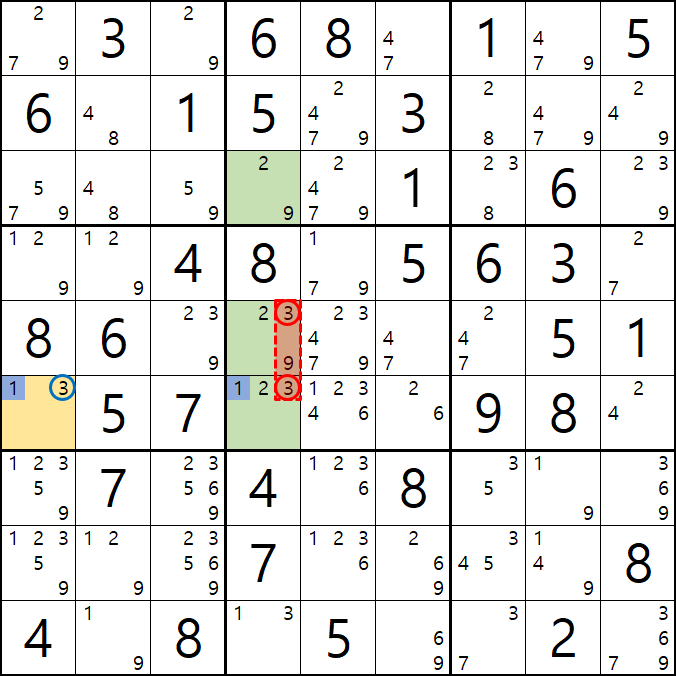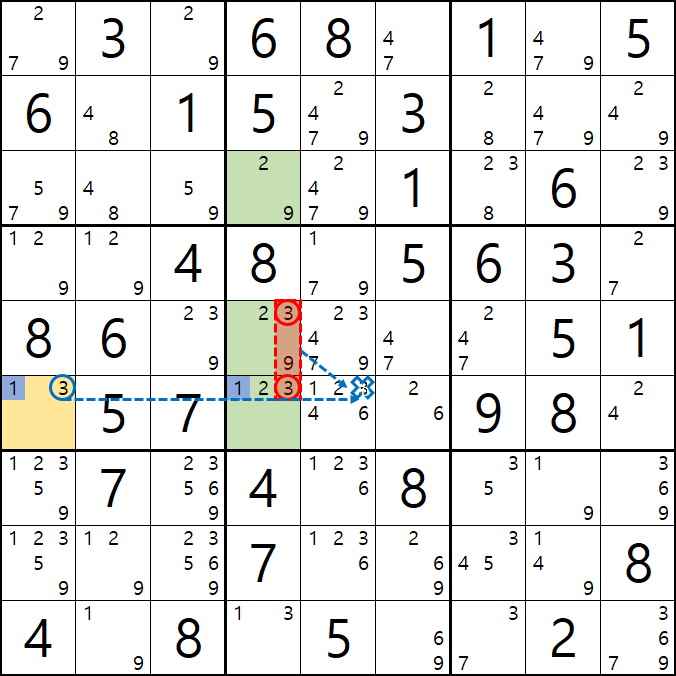
1/3[F1] 과 1/2/3[F4], 2/3[E4], 2/9[C4]의

2개의 1/3/X + 1/2/3/9의 거의 잠긴 세트에서

 

제한된 공통 후보숫자 1을 제외한 후보숫자 중

 

3[F1]과 3[F4&E4] 이 동시에 마주보는 3[F5]를 제거할 수 있다. 

 

3. ALS RULE1-3탄. (1+5)

 

 

5/7[I5] 와 2/5/6/7[D5], 2/6/7[D6], 4/7[E4], 2/4/7/8[E6], 2/4/6/7/8[F6]의

2개의 5/7/X + 1/2/5/6/7/8의 거의 잠긴 세트에서

 

제한된 공통 후보숫자 5를 제외한 후보숫자

 

7[I5]와 7[D5&D6&E4&E6&F6]가 동시에 마주보는 8[F5]를 제거할 수 있다. 

 

4. ALS RULE1-4탄. (2+4)

 

 

1/2[A2],2/7[A7] 와 1/2[G2], 6/7/8[G5], 6/7/8[G6], 2/7/8[G9]

2개의 1/2/7 + 1/2/6/7/8의 거의 잠긴 세트에서

 

제한된 공통 후보숫자 1을 제외한 후보숫자 중

 

7[A7]와 7[G8&G6&G9]가 동시에 마주보는 7[G7]을 제거할 수 있다. 

 

자! 지금까지는 ALS RULE1에 대해 알아 봤고

 

다음은 제한된 공통 후보숫자가 2개인 경우를 알아보자! (나도 반만 이해했다. 3개인 경우도 있을 거 같긴 하지만 아직 사례는 못 찾았다.)

 

5. ALS RULE2-1탄. (3+2), 제한된 공통 후보숫자 2개

 

5-1. 스탭1- 공통후보숫자 2번

 

아래 움짤과 같이 

 

 

 

2/7/9[B2],4/7/9[A3], 7/9[A9]와 1/2[D2], 1/2/4[D3]

2개의 2/4/7/9 + 1/2/4의 거의 잠긴 세트에서

 

제한된 공통 후보숫자 2를 제외한 후보숫자 중

 

4[A3]과 4[D3] 이 동시에 마주보는 4[A3]와 4[F3]을 제거할 수 있고, 

 

5-2. 스탭2- 공통후보숫자 4번

 

2/7/9[B2],4/7/9[A3], 7/9[A9]와 1/2[D2], 1/2/4[D3]

2개의 2/4/7/9 + 1/2/4의 거의 잠긴 세트에서

 

제한된 공통 후보숫자 4를 제외한 후보숫자 중

 

2[B2]와 2[D2]가 동시에 마주보는 2[A2]를 제거할 수 있고, 

 

5-3. 스탭3- 공통후보숫자 2, 4번

 

2/7/9[B2],4/7/9[A3], 7/9[A9]와 1/2[D2], 1/2/4[D3]

2개의 2/4/7/9 + 1/2/4의 거의 잠긴 세트에서

 

복수의 제한된 공통 후보숫자 중 2, 4를 제외한 후보숫자 중

 

1[D2]와 1[D3]이 동시에 마주보는 (이번 게임에서는 페어 제거 효과를 낸다)

1[D1], 1[D9], 1[E1], 1[E3], 1[F1], 1[F2], 1[F3]를 제거할 수 있다. 

 

위의 스탭 1~3을 합쳐보면

 

 

2/7/9[B2],4/7/9[A3], 7/9[A9]와 1/2[D2], 1/2/4[D3]

2개의 2/4/7/9 + 1/2/4의 거의 잠긴 세트에서

 

제한된 공통 후보숫자 2를 제외한 후보숫자 중

4[A3]과 4[D3] 이 동시에 마주보는 4[A3]와 4[F3]을 제거할 수 있고, 

 

제한된 공통 후보숫자 4를 제외한 후보숫자 중

2[B2]와 2[D2]가 동시에 마주보는 2[A2]를 제거할 수 있고, 

 

복수의 제한된 공통 후보숫자 중 2, 4를 제외한 후보숫자 중

1[D2]와 1[D3]이 동시에 마주보는1[D1], 1[D9], 1[E1], 1[E3], 1[F1], 1[F2], 1[F3]를 제거할 수 있다. 

 

가 되겠다. 

 

 확실한 페어 및 확실한 트리플(가능하면 확실한 쿼드까지)을 많이 보고 잘 찾는 것이 고급 기술에서 매우 유용하구나~ 라는 생각을 하게 된다. 

 

'스도쿠/초고급(저세상레벨)' 카테고리의 글 목록

 

11월 29일 추가 > 최근에 ALS를 적용해 보니 아래 링크와 같이 XY 체인을 찾고 감각적으로 푸는데 매우 좋다는 것을 알게 되었다. 

 

XY 체인을 ALS 공식으로 좀 더 쉽게 찾고 풀기