움짤로 익히는 스도쿠 19. 수-드-콕(Sue-De-Coq)
- 스도쿠 / 고급
- 2024. 11. 25.
이번 글에서는 지난 포스티엥서 쓴 ALS와 비슷한 풀이법을 가진 수-드-콕(Sue-De-Coq) 이라는 스도쿠 기술에 대해 알아 보도록 하겠다. 명칭의 유래는 발견자인 수-드-콕(Sue-De-Coq) 박사(?)의 이름을 붙인 것이고 작동원리는 거의 잠긴 세트(=ALS)라는 공식과 궤를 같이 한다. 다만 나는 이 기술을 사용하는 방법은 설명할 수 있지만 증명할 수는 없다.
ALS 기초 개념을 알면 이해하는데는 어렵지 않다. ALS에 대한 것은 아래에 적겠다. 수-드-콕(Sue-De-Coq)은 찾기가 용이해서(경우에 따라서는 암산도 가능한) 고급 기술로 적어 본다.
처음 접하는 스도커는 아마 WXYZ윙과 닮았다고 느낄 수도 있다. 맞다. 눈에 보이는 패턴은 비슷하지만 접근이 전혀 다르다~
일단 ALS의 개념은 간단하다 Almos Lock Set의 준말로 한국말로 하면 거의 잠긴 세트 정도로 보면 되겠다.
우리가 아는 Lock Set은 간단하다.
1/2 - 1/2 << 2칸이 있으면 잠긴 세트 (Lock Set)라고 부른다.
1/2/3 - 1/2 - 1/3 << 3칸이 있으면 잠긴 세트 (Lock Set)라고 부른다.
1/2/3 - 1/2/4 - 1/3 - 2/4 << 4칸이 있으면 잠긴 세트 (Lock Set)라고 부른다.
1/2/4/5 - 1/2/5 - 2/3/4 - 1/5 - 3/4/5 << 5칸이 있으면 잠긴 세트 (Lcok Set)라고 부른다.
즉, N개의 후보숫자가 N개의 칸에 조합된 상태를 Lock Set로 보면 되겠다.
그럼 거의 잠긴 세트 (ALS)는
잠긴 세트를 이루는 N개의 후보수 조합에서 1칸이 빠진 것을 말한다.
1/2/3 - 1/2 또는
1/2/3 - 1/3 또는
1/2 - 1/3 의 2칸으로 존재하는 조합을
1/2/3에 대한 거의 잠긴 세트 (=또는 잠기다 만 세트, 조건만 맞으면 잠기는 세트) 로 보면 되겠다.
1/2/3 - 1/2/4 - 1/3 또는
1/2/3 - 1/2/4 - 2/4 또는
1/2/3 - 1/3 - 2/4....의
3칸으로 존재하는 조합을
1/2/34에 대한 거의 잠긴 세트 ALS라고 한다.
1/2/4/5 - 1/2/5 - 2/3/4 - 1/5 또는
1/2/4/5 - 1/2/5 - 2/3/4 - 3/4/5 또는
1/2/4/5 - 1/2/5 - 1/5 - 3/4/5.... 의 4칸으로 존재하는 조합을
1/2/3/4/5에 대한 거의 잠긴 세트 ALS라고 한다.
위의 ALS에서 1칸이 더 빠지면 AALS라고 불러서 AALS공식이라고도 부른다.
즉, N개의 후보숫자가 N-1(이상)개 칸에 적게 조합된 상태를 Almost Lock Set로 보면 되겠다.
자 이제 본격적인 게임에 들어가보자.
형태 자체는 WXYZ윙과 닮기도 했지만 개념 자체는 다르다. WXYZ윙은 완전히 잠긴 Lock Set이고 수드콬은 덜 잠긴 Almost Lock Set이기 때문에 이중값을 넘어서 삼중값, 사중값.. 까지도 나온다.
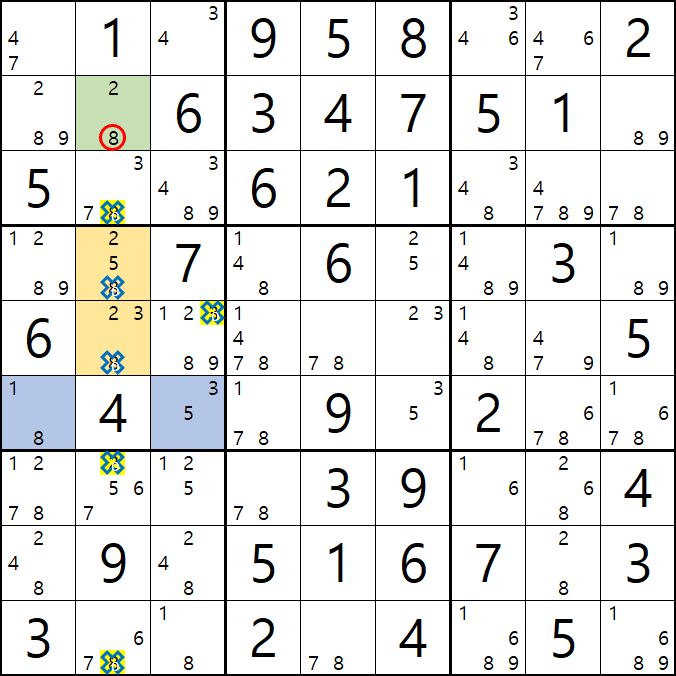
움짤 예제 1. 핀 1+1, 피벗2 의 수-드-콕(Sue-De-Coq)

위의 움짤과 같이
2열에 2/8[B2], 2/5/8[D2], 2/3/8[E2] ALS(2/3/5/8) 1세트와
박스4에 2/5/8[D2], 2/3/8[E2], 3/5[F3] ALS(2/3/5/8) 1세트가 존재할 때,
( 핀이 되는 2/8[B2]와 3/5[F3] 에는 겹치는 숫자가 없고
핀이 공유하는 피벗인 2/5/8[D2], 2/3/8[E2] 에는 2개의 핀에 존재하는 모든 후보숫자가 있는 것을 알 수 있다. )
이 때, 핀 2칸과 피벗 2칸 총 4칸에 존재하는 후보숫자가 동시에 마주보는 다른 칸의 동일 후보숫자를 삭제할 수 있다.
따라서
2열 에서는
2/8[B2], 2/5/8[D2], 2/3/8[E2], 3/5[F3] 중에서
2[B2], 2[D2], 2[E2] 이 동시에 보는 2[G2]를
8[B2], 8[D2], 8[E2] 이 동시에 보는 8[C2], 8[I2]을
박스4 에서는
3[E2], 3[F3] 이 동시에 보는 3[F3]을
제거할 수 있다.
움짤 예제 2. 핀 1+2, 피벗2 의 수-드-콕(Sue-De-Coq)
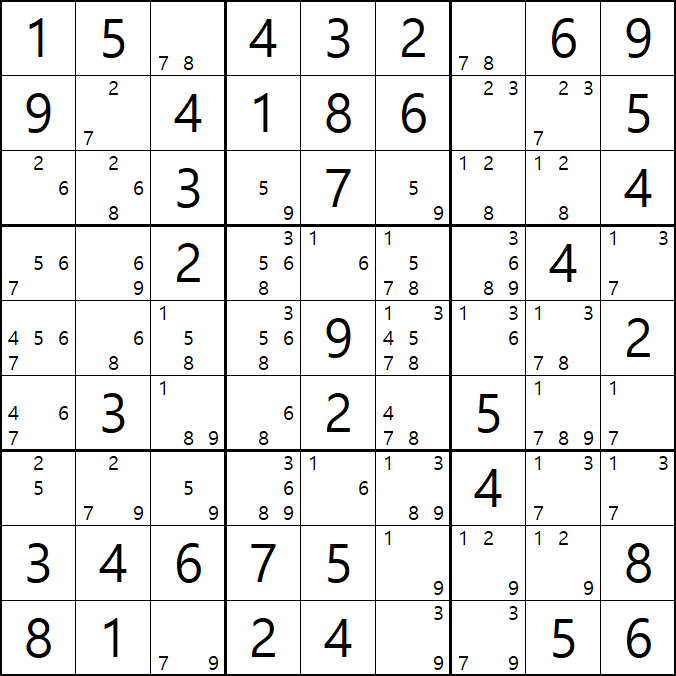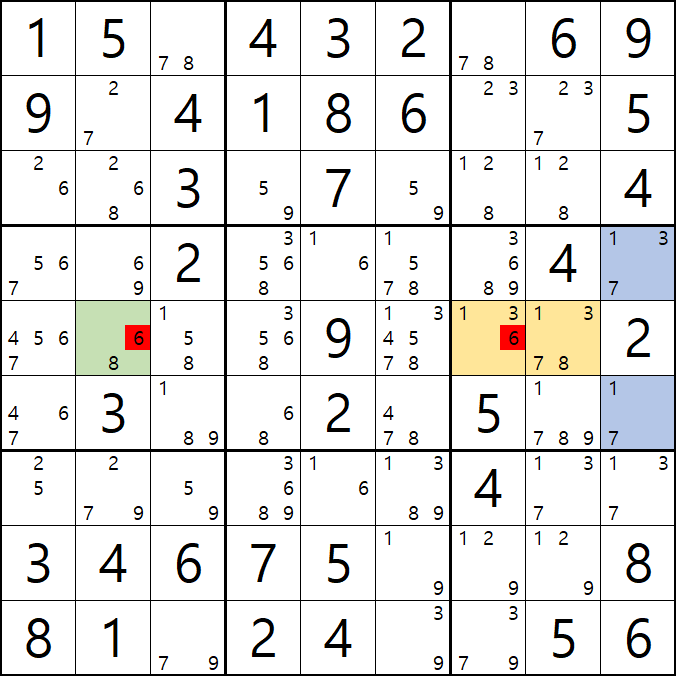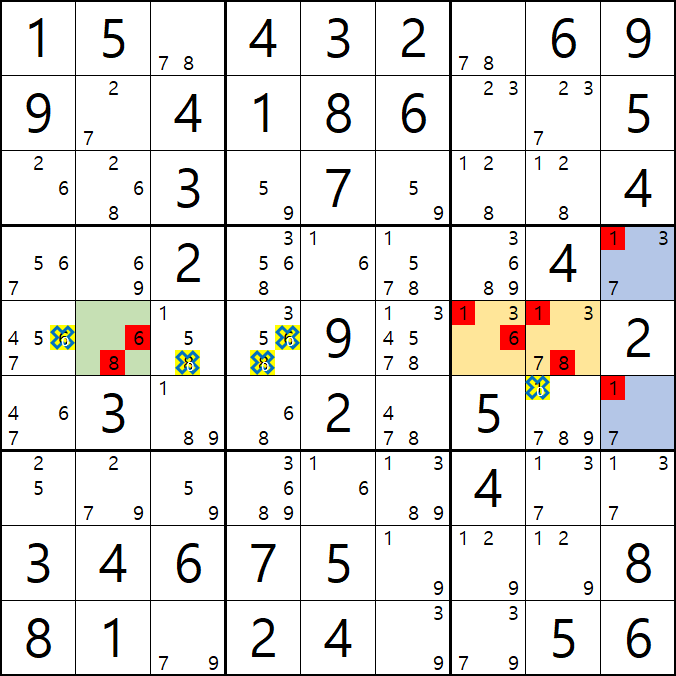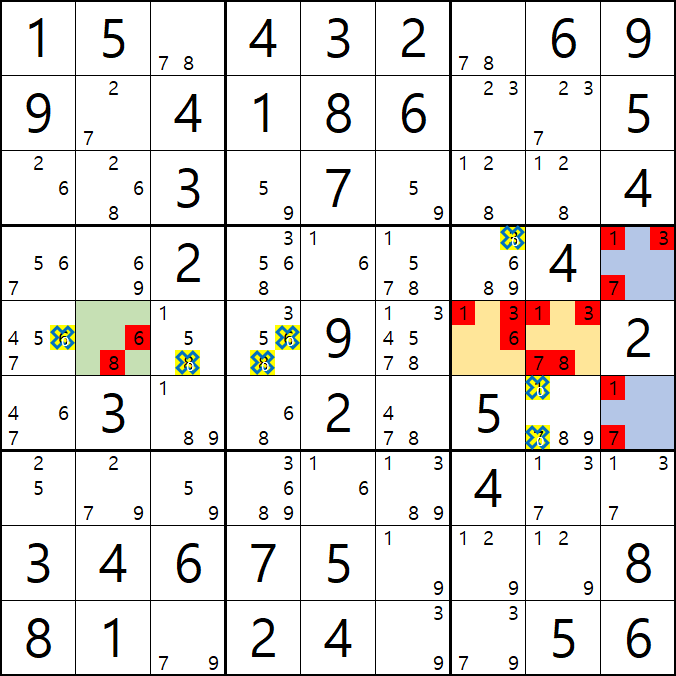
위의 움짤과 같이
D행에 6/8[E2], 1/3/6[E7], 1/3/7/8[E8] AALS(1/3/6/7/8) 1세트와
박스6에 1/3/6[E7], 1/3/7/8[E8], 1/3/7[D9], 1/7[F9] ALS(1/3/6/7/8) 1세트가 존재할 때,
( 핀이 되는 6/8[E2]와 1/3/7[D9], 1/7[F9] 에는 겹치는 숫자가 없고
핀이 공유하는 피벗인 1/3/6[E7], 1/3/7/8[E8] 에는 3개의 핀에 존재하는 모든 후보숫자가 있는 것을 알 수 있다. )
이 때, 핀 3칸과 피벗 2칸 총 5칸에 존재하는 후보숫자가 동시에 마주보는 다른 칸의 동일 후보숫자를 삭제할 수 있다.
따라서
2열에서는
6/8[E2], 1/3/6[E7], 1/3/7/8[E8], 1/3/7[D9], 1/7[F9] 중에서
6[E2], 6[E7] 이 동시에 보는 6[E1], 6[E4]을
8[E2], 8[E8] 이 동시에 보는 8[E3], 8[E4]을
박스6 에서는
1[E7], 1[E8], 1[D9], 1[F9] 이 동시에 보는 1[F8]을
3[E7], 3[E8], 3[D9] 이 동시에 보는 3[D7]을
7[E8], 7[D9], 7[F9] 이 동시에 보는 7[F8]을
제거할 수 있다.
움짤 예제 3. 핀 1+1, 피벗3 의 수-드-콕(Sue-De-Coq)
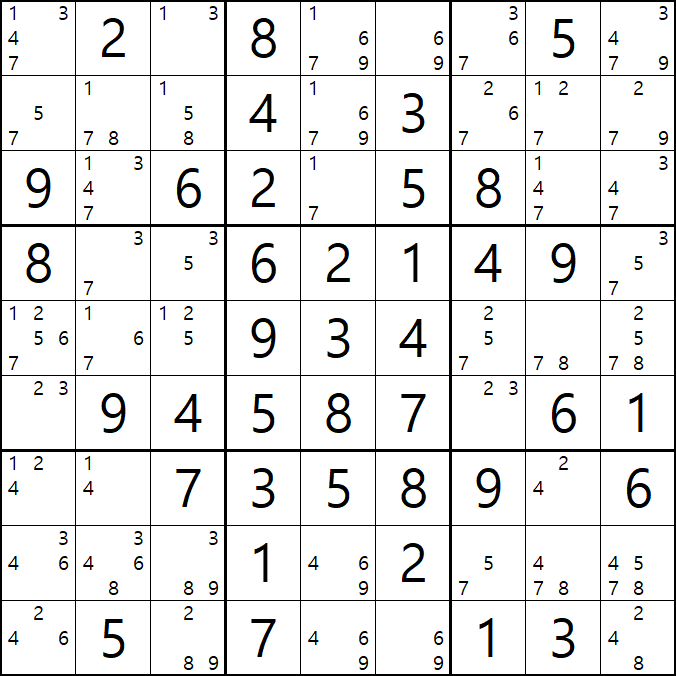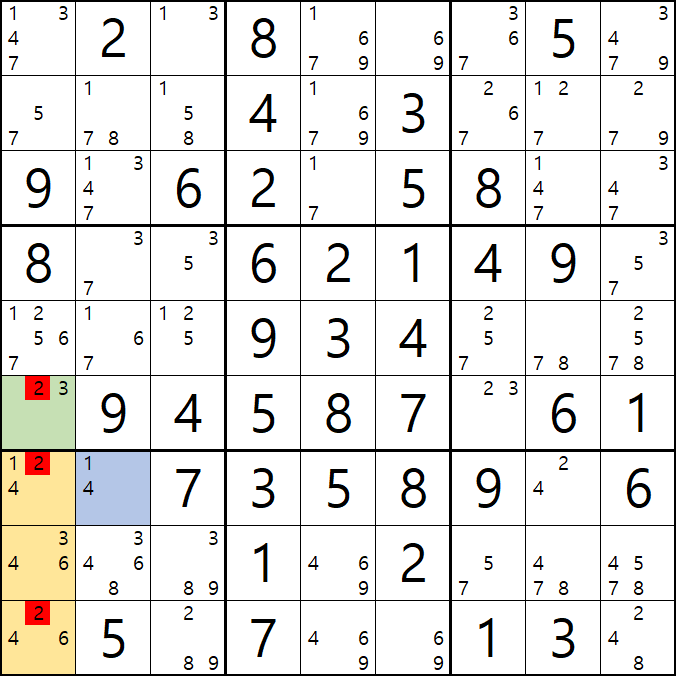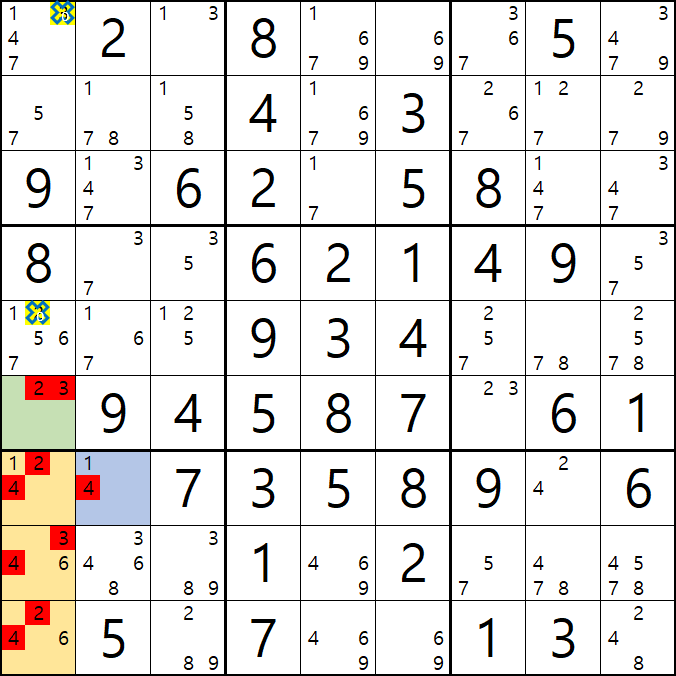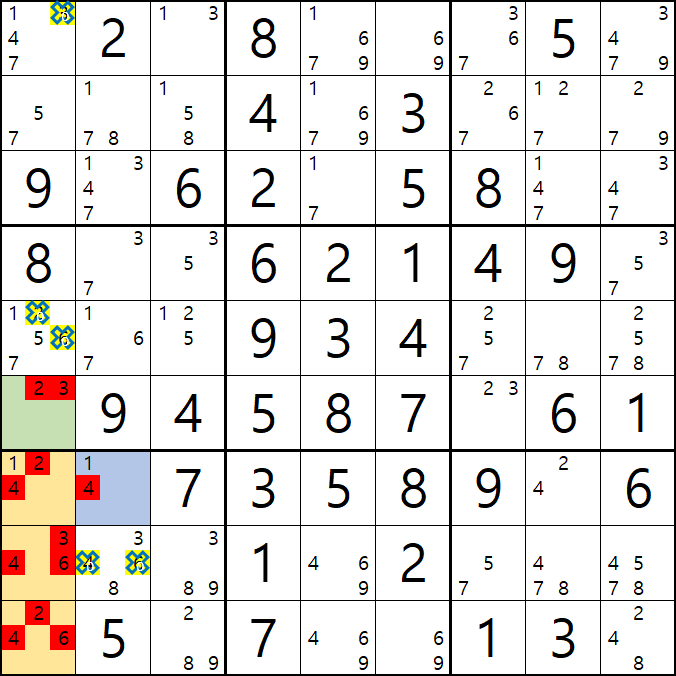
위의 움짤과 같이
1열에 2/3[F1], 1/2/4[G1], 3/4/6[H1], 2/4/6[I1] ALS(1/2/3/4/6) 1세트와
박스7에 1/2/4[G1], 3/4/6[H1], 2/4/6[I1], 1/4[G2] ALS(1/2/3/4/6) 1세트가 존재할 때,
( 핀이 되는 2/3[F1]와 1/4[G2] 에는 겹치는 숫자가 없고
핀이 공유하는 피벗인 1/2/4[G1], 3/4/6[H1], 2/4/6[I1] 에는 2개의 핀에 존재하는 모든 후보숫자가 있는 것을 알 수 있다. )
이 때, 핀 2칸과 피벗 3칸 총 5칸에 존재하는 후보숫자가 동시에 마주보는 다른 칸의 동일 후보숫자를 삭제할 수 있다.
따라서
1열에서는
2/3[F1], 1/2/4[G1], 3/4/6[H1], 2/4/6[I1], 1/4[G2] 중에서
2[F1], 2[G1], 2[I1] 이 동시에 보는 2[E1]을
3[F1], 3[H1] 이 동시에 보는 3[A1]을
박스7 에서는
4[G1], 4[H1], 4[I1], 4[G2] 가 동시에 보는 4[H2]를
3[E7], 3[E8], 3[D9] 이 동시에 보는 3[D7]을
2개의 하우스(1열과 박스7)를
모두 한 번에 보는 피벗의 후보숫자 그룹
6[H1], 6[I1] 이 동시에 보는 1열의 6[F8]과 박스7의 6[H2]을
제거할 수 있다.
위의 3가지 예제로 보면 박스안의 칸은 3X3으로 피벗이 되는 칸은 최대 3칸, 핀이 되는 칸은 최대 2칸까지 가능하므로
주로 찾아야 하는 숫자는 4~6개까지겠지만 주로 4~5개가 될 것으로 보고 서칭하면 좋을 것이라고 본다.
또한 조건만 맞으면 최대 6개 종류의 후보숫자를 제거하는 게임 체인저가 되므로 설령 이해가 안가더라도 위에 설명한 현상만 이해해 보자. 나중에 초고급 문제들에 접하면 분명히 쉬우면서 유용할 것이다.
자 이렇게 3가지의 예제가 내가 수-드-콕(Sue-De-Coq)에 설명할 수 있는 전부다.
쉽게 증명하는 방법을 알아내면 추가해서 올리도록 하겠다. 즐~스~
음 또한 이 공식은 APE라는 저 세상 공식과 연계가 51% 확률로 되는 거라고 생각한다. (스드콕은 피벗에 핀의 숫자가 전부 포함. APE는 일부만 포함 된다) 한 번 아래 링크에서 둘러보기 바란다. (최근에 좀 어려운 공식들을 접하다 보니까 푸는 방법보다 찾는 방법이 참 어렵다고 느껴진다.)
움짤로 익히는 스도쿠 20. 정렬된 쌍 배제 공식 I(APE)
움짤로 익히는 스도쿠 21. 정렬된 쌍 배제 공식 II(APE)
움짤 예제 1.은
수-드-콕(Sue-De-Coq) 공식 적용 후
바로
APE라는 공식을 적용하면
아래 짤과 같이 추가로 B2가 8로 확정이 된다.