움짤로 익히는 스도쿠 17. WXYZ 윙

 이번 글에서는 XY윙 > XYZ윙에서 좀 더 확장된 개념인 WXYZ윙에 대해 알아보도록 하겠다. 명칭에서 알 수 있듯이 4개의 미지수가 1개의 하우스가 아닌 2개 이상의 하우스에 걸쳐서 확실한 쿼드러플을 이룰 때, 다른 칸의 후보숫자를 제거하는 공식이 되겠다. 느낌은 4개의 확실한 쿼드러플 상태일 때 잠긴 세트에 맞는 후보 숫자 중에 페어, 트리플, 쿼드제거를 한다고 보면 되겠다. (이 글은 최소한 XY윙은 이해하는 스도커가 본다고 가정하고 쓴다. 만약 위의 XY윙 공식을 모른다면 일단 알아보고 오자.)

 

스도쿠 8. X윙, Y윙, XY윙 공식을 알아보자

 

 XY윙이나 XYZ윙이 좀 정형화 되어 있다면 WXYZ윙은 숫자가 조합되는 가지수가 많아서 정형화 되지 않아 헷갈리기 쉽지만 개념만 확실한 쿼드러플에 대해 이해하고 있다면 XY윙 및 XYZ윙만큼 쉽고 유용하다. 바로 출발하겠다. 

 

 미리 양해를 구하자면, 모든 경우의 수를 체인으로 증명할 수 있으면 좋겠지만 나의 실력으로는 100%는 불가능하다. 현상으로 이해하자~ (물론 체인으로 증명할 수 있는 경우도 있긴 하다~)

 

1. 클래식한 WXYZ

 

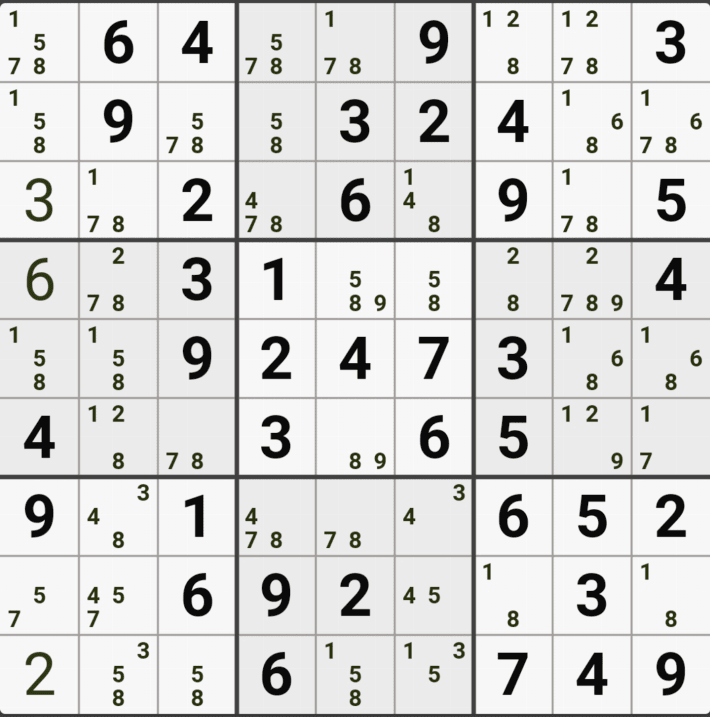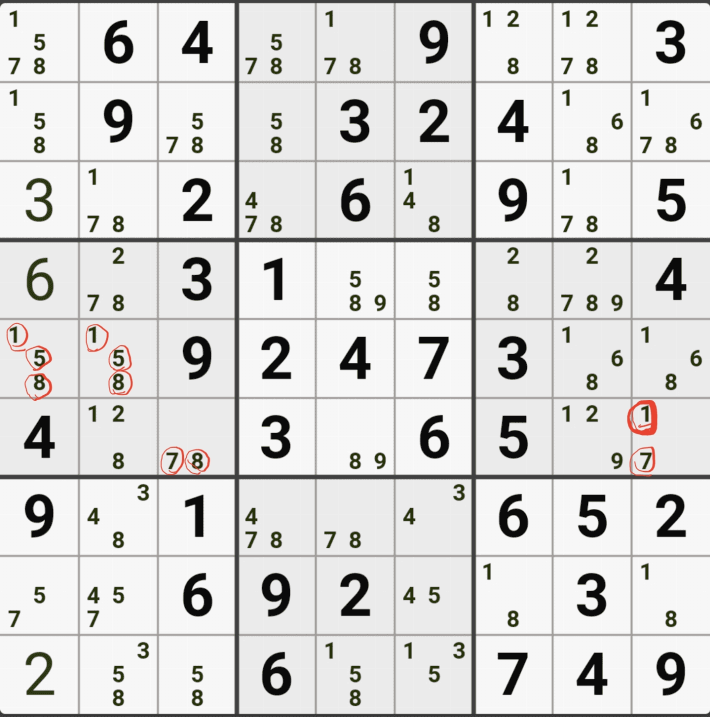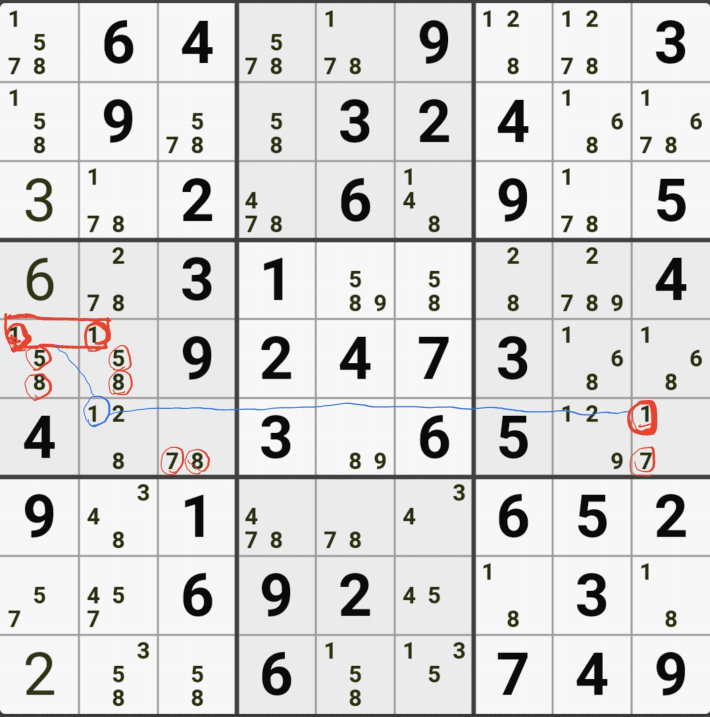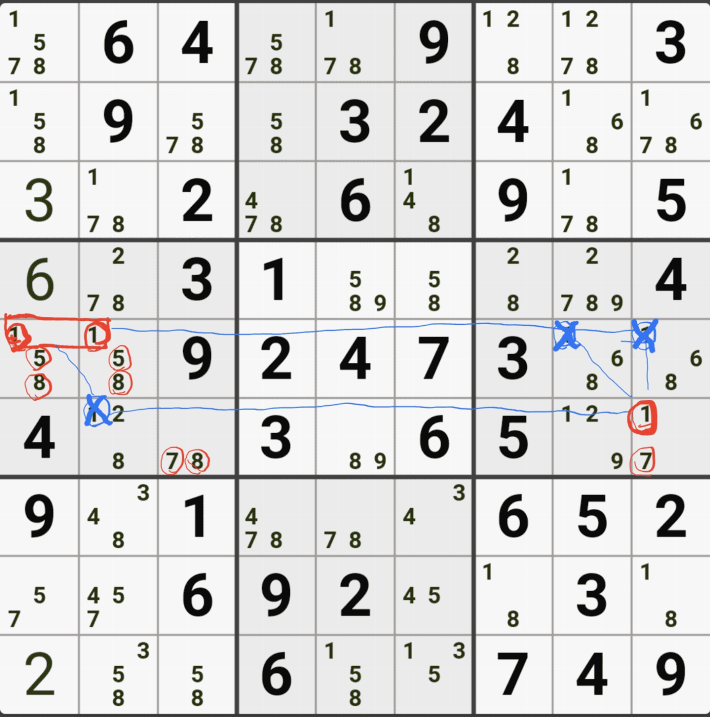
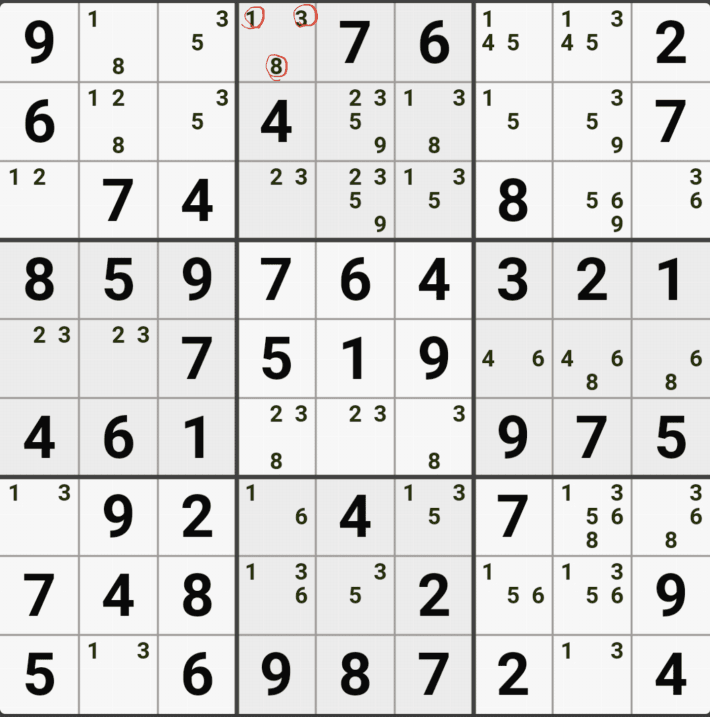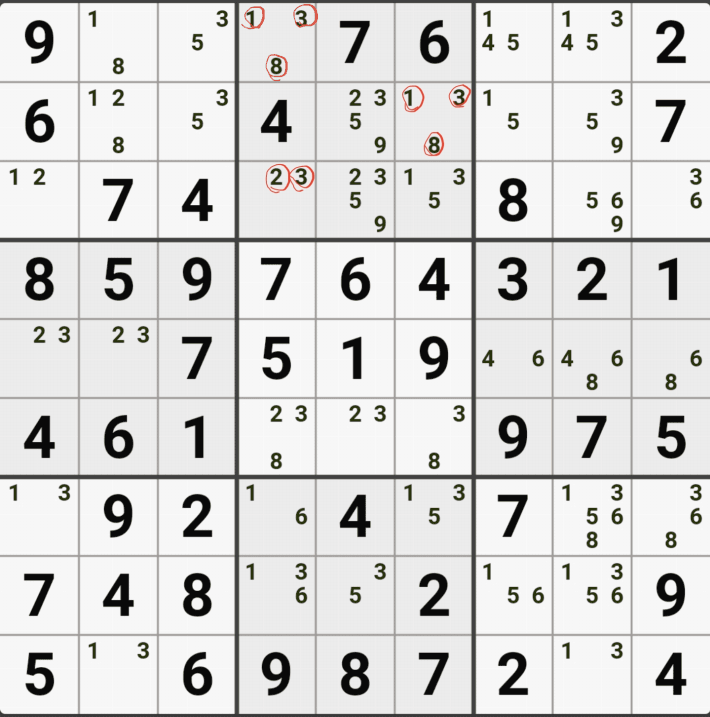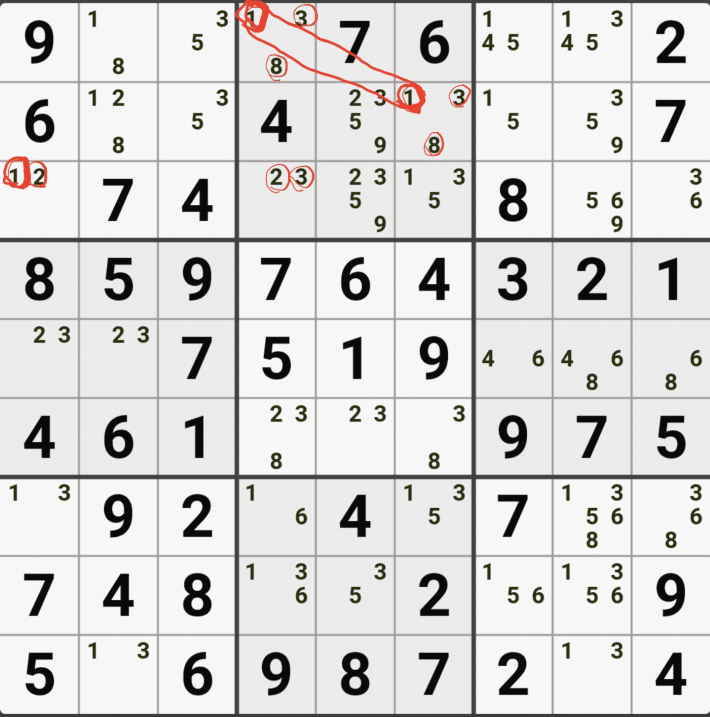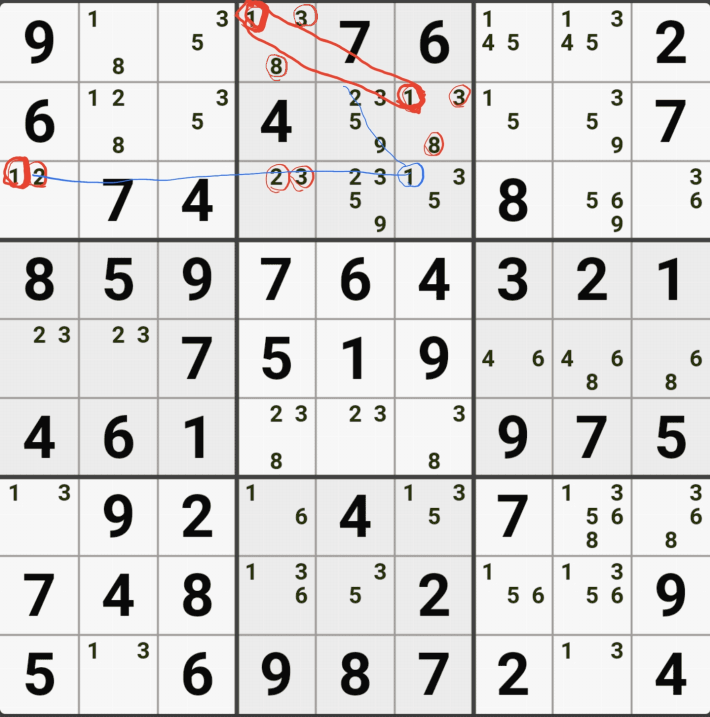
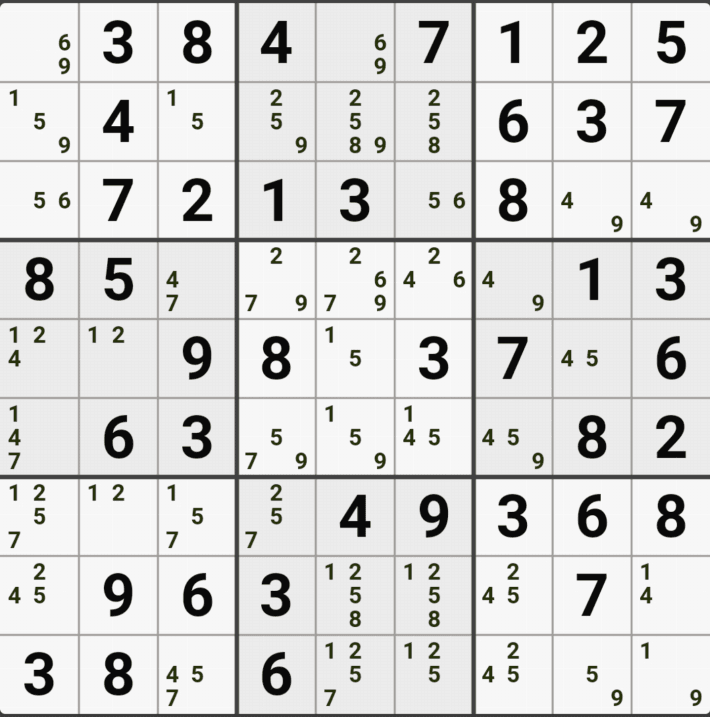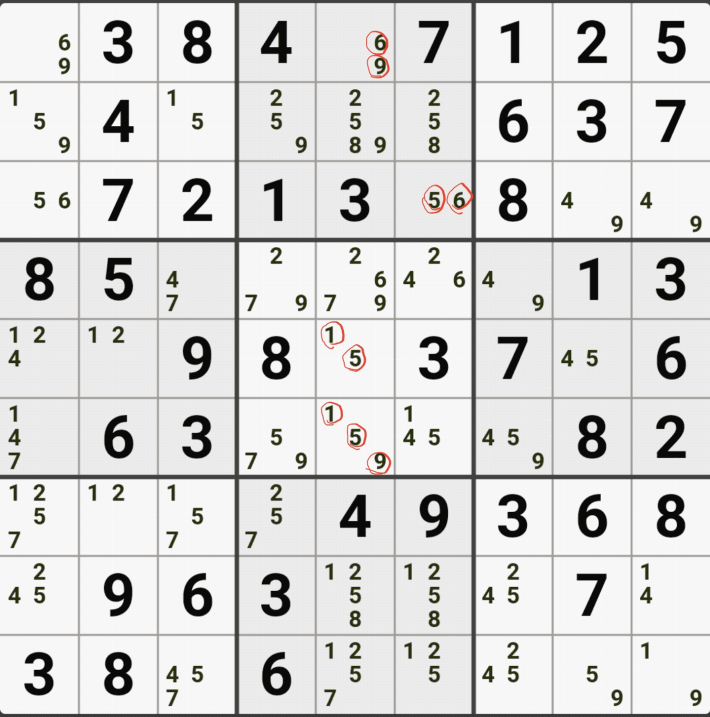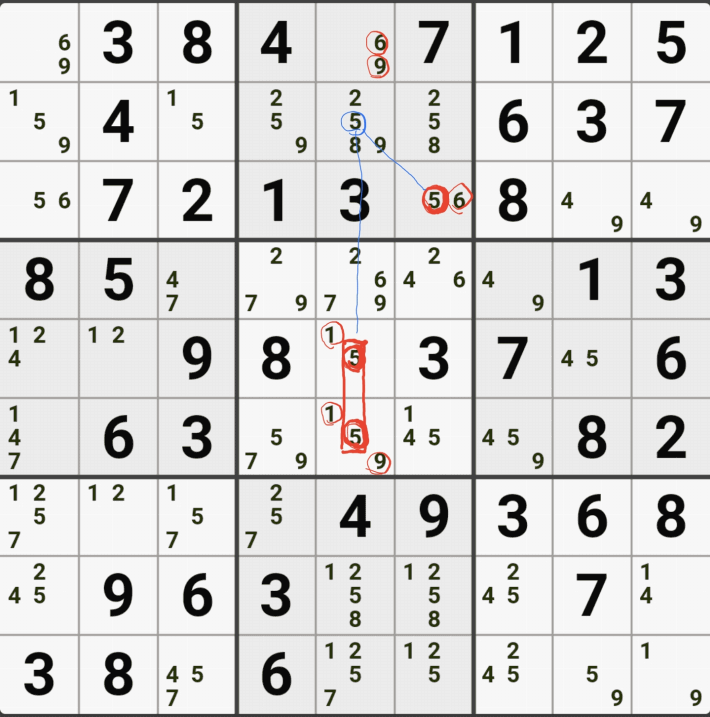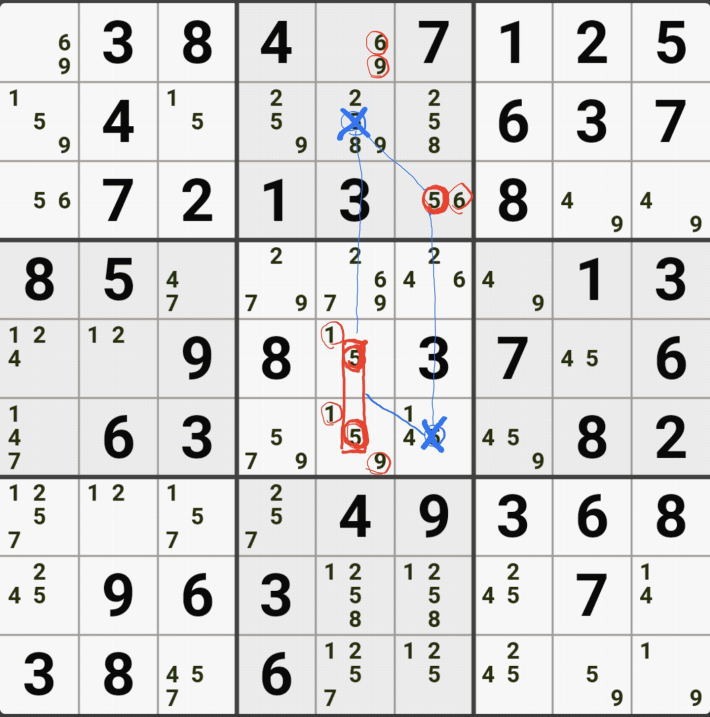
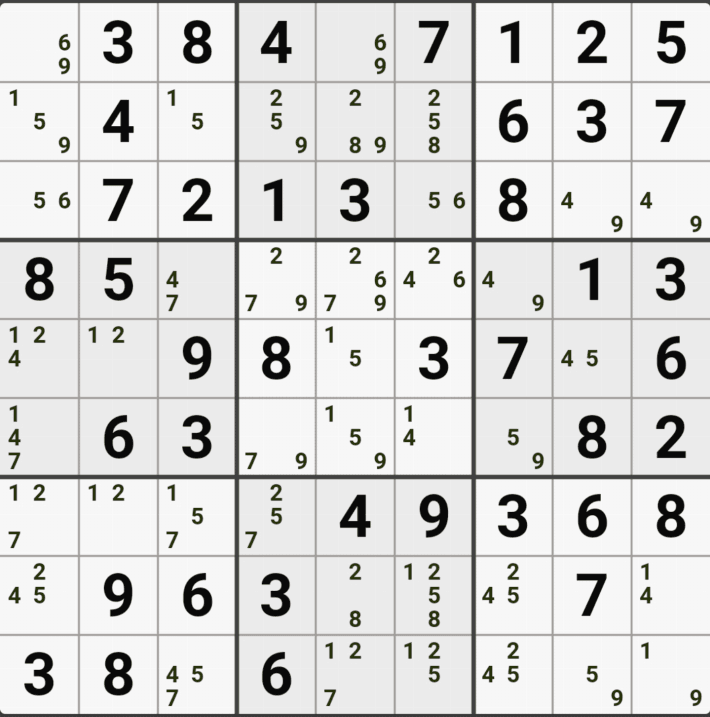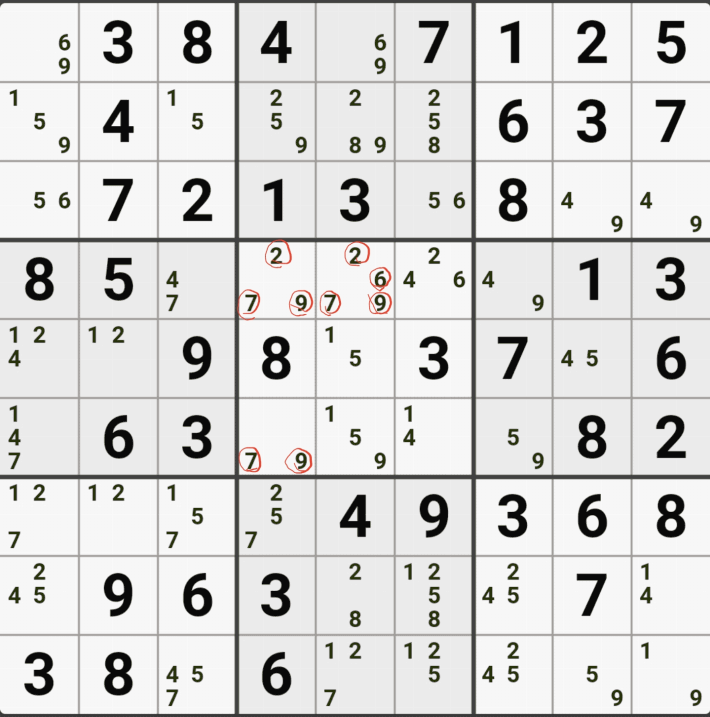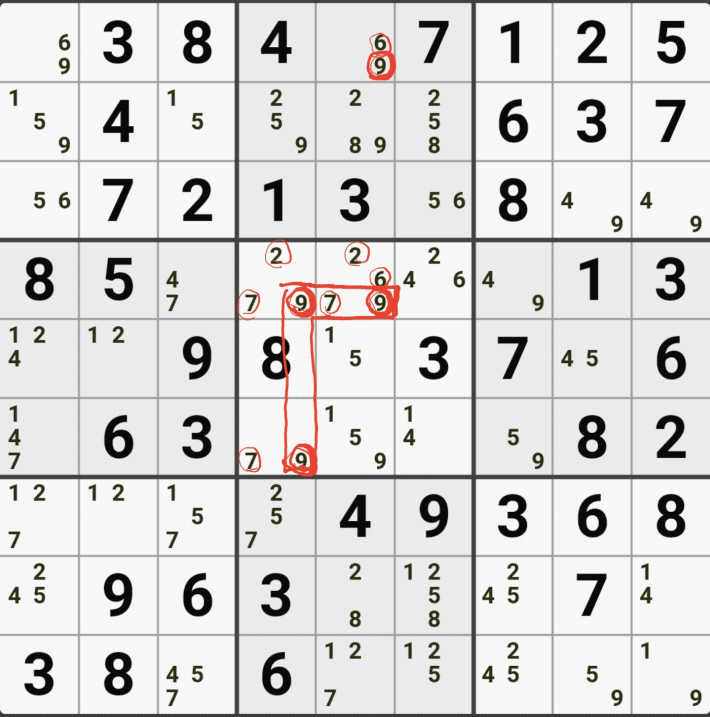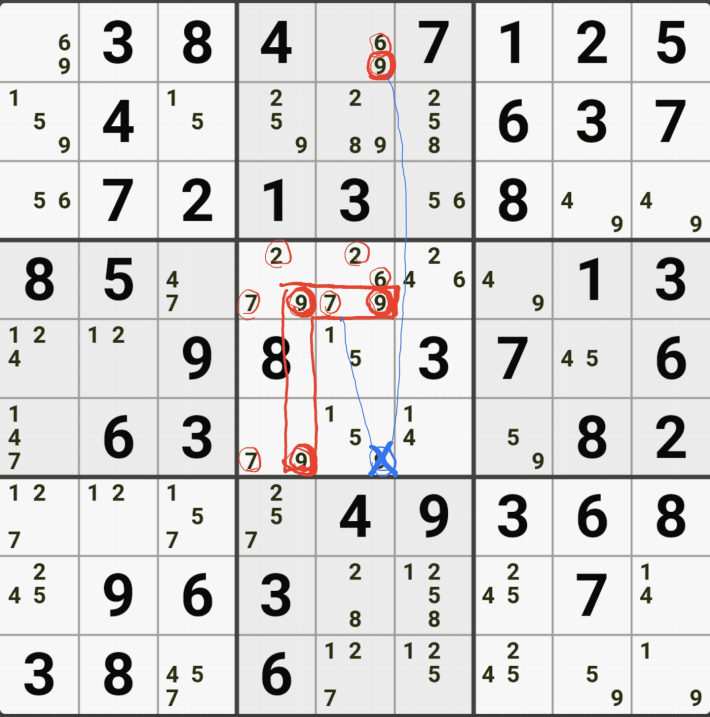
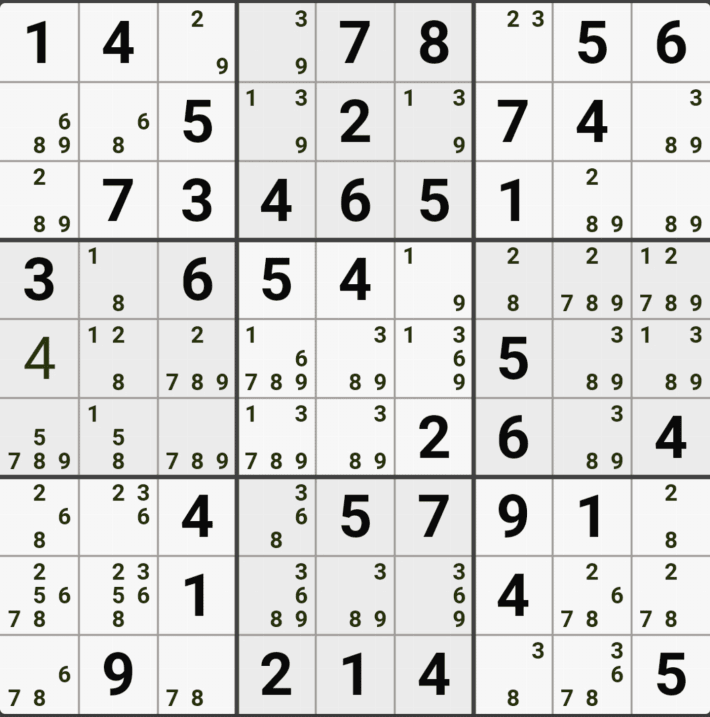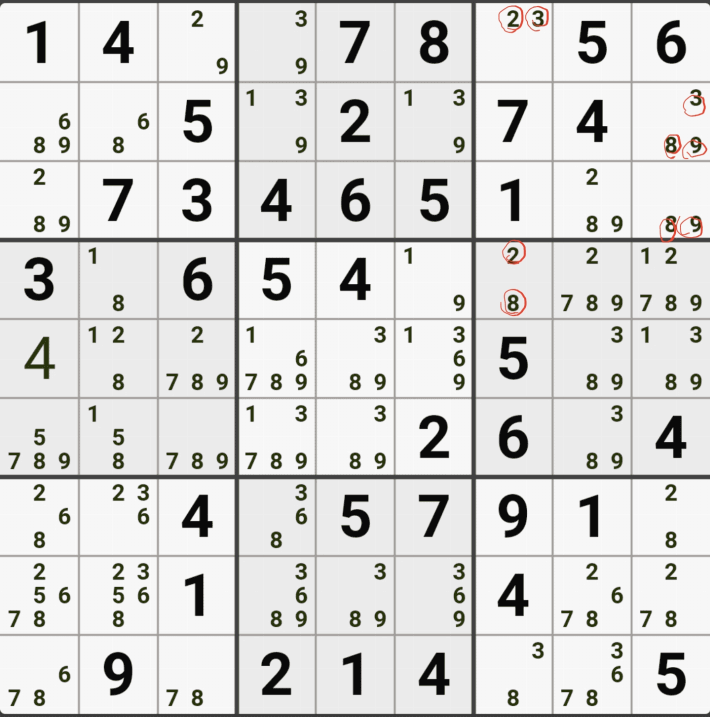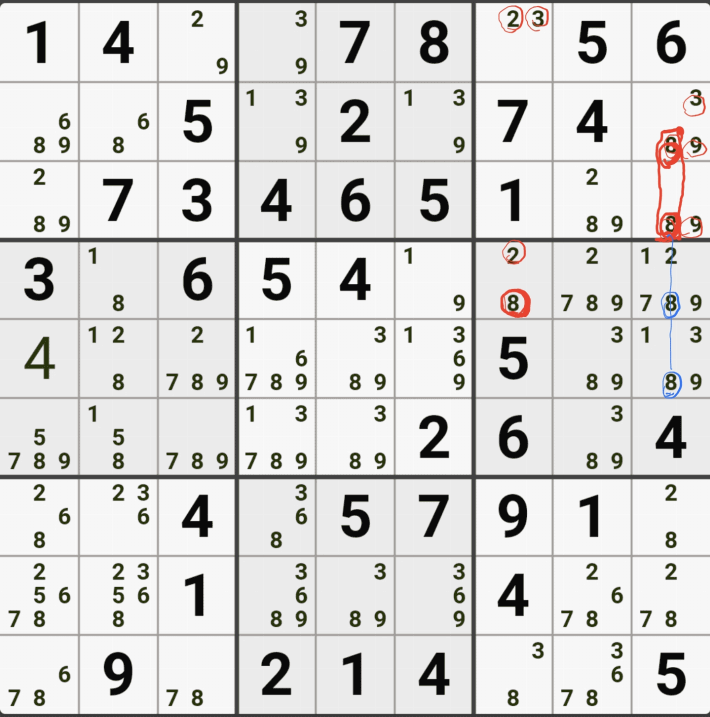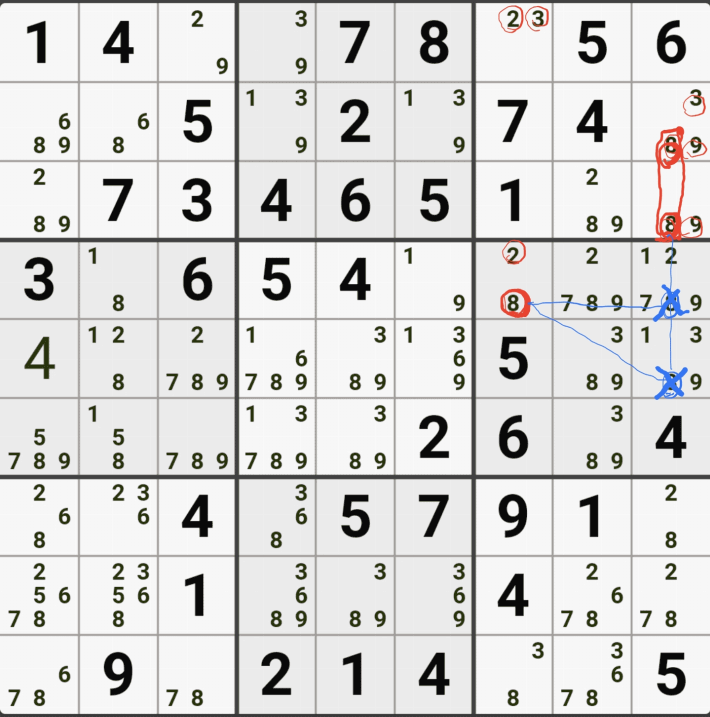
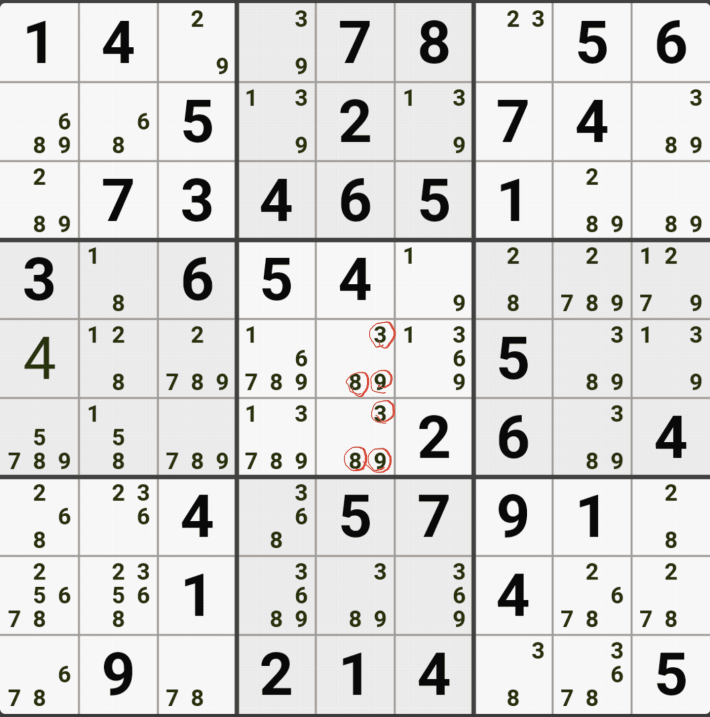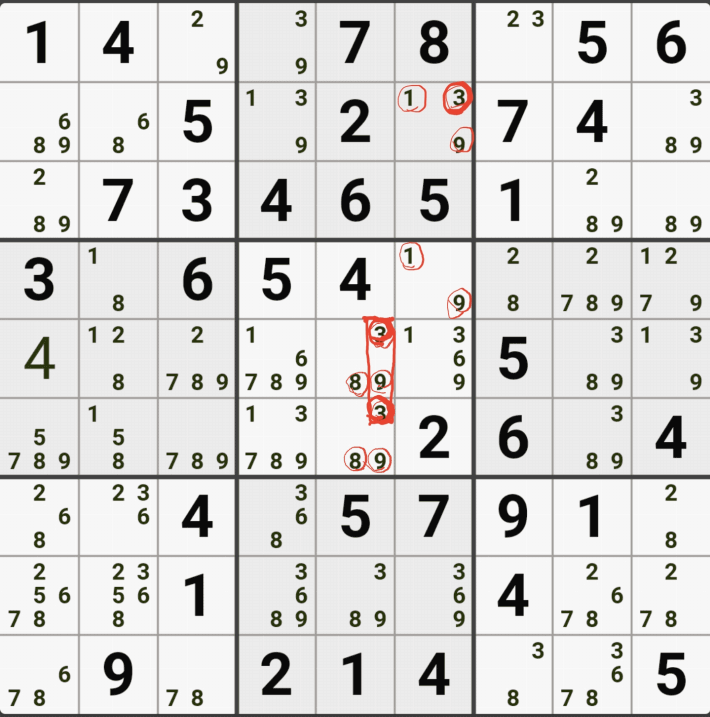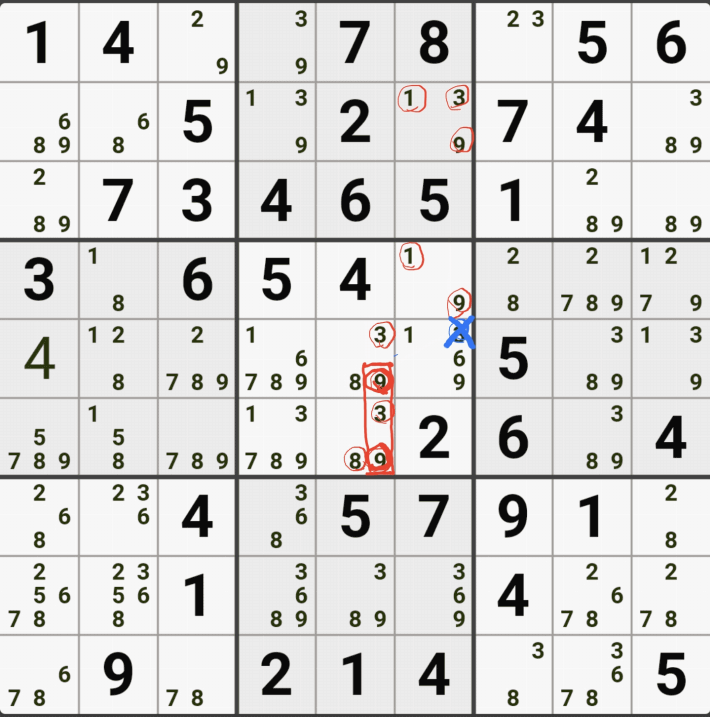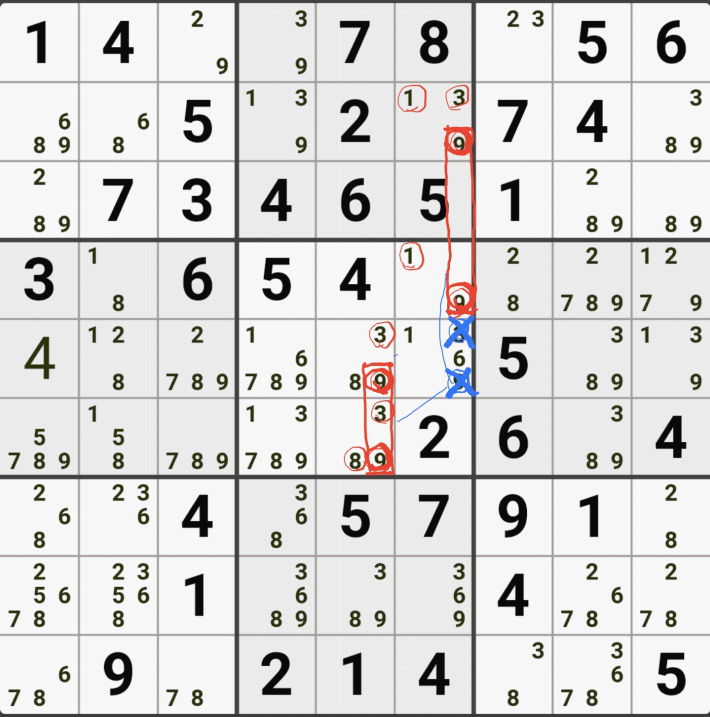
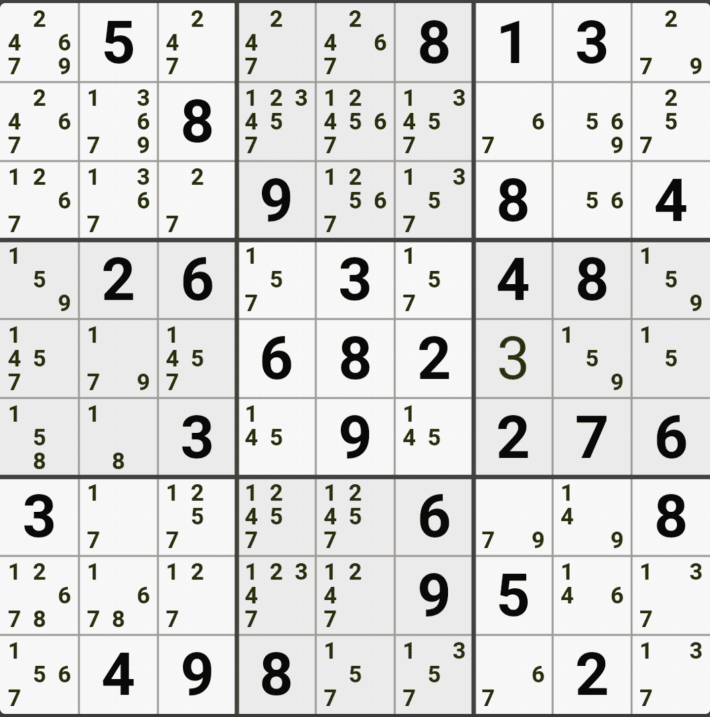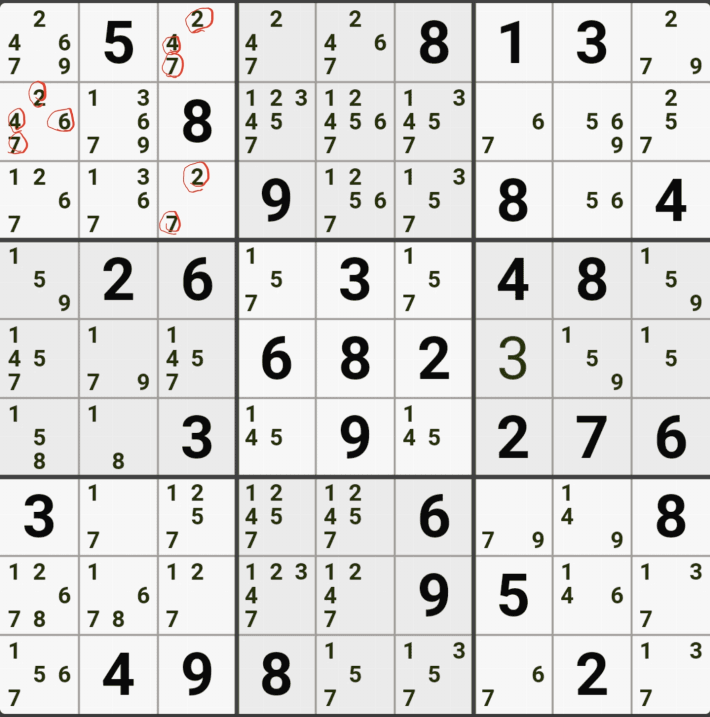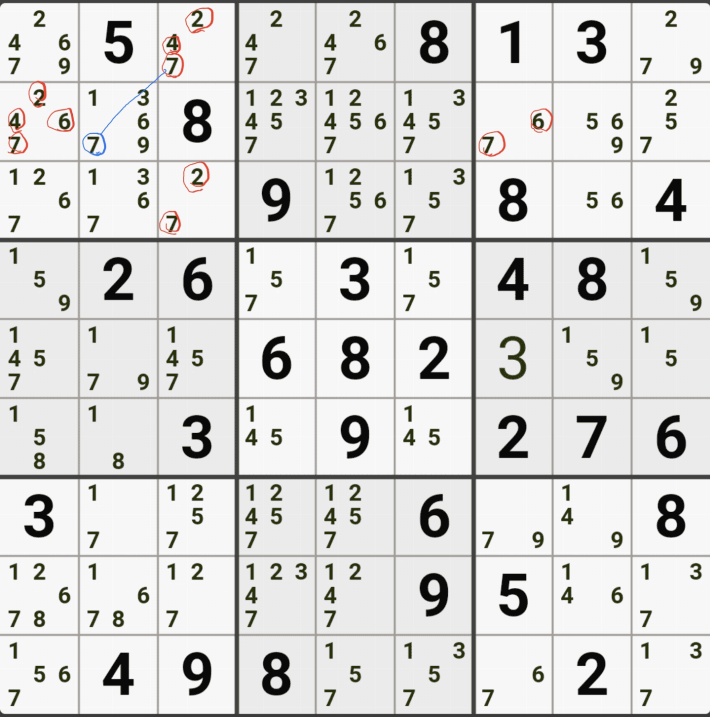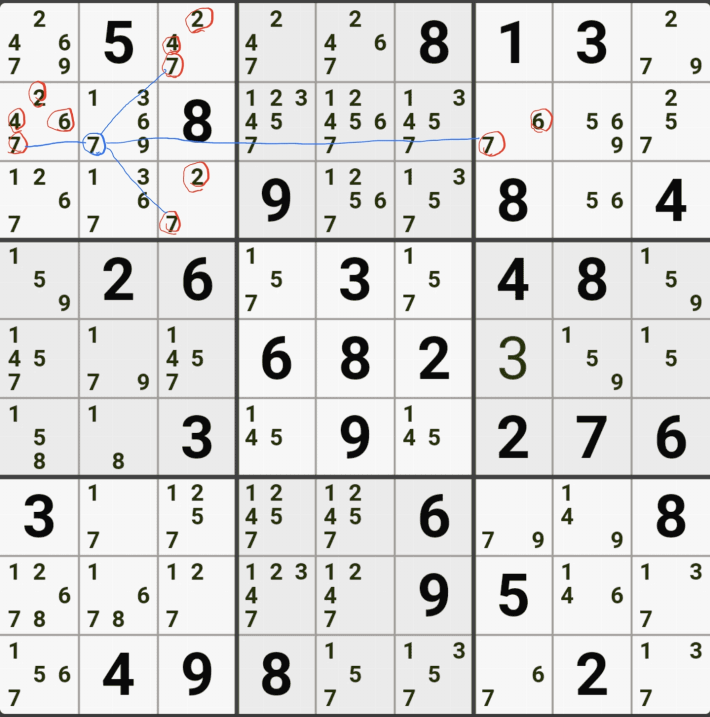
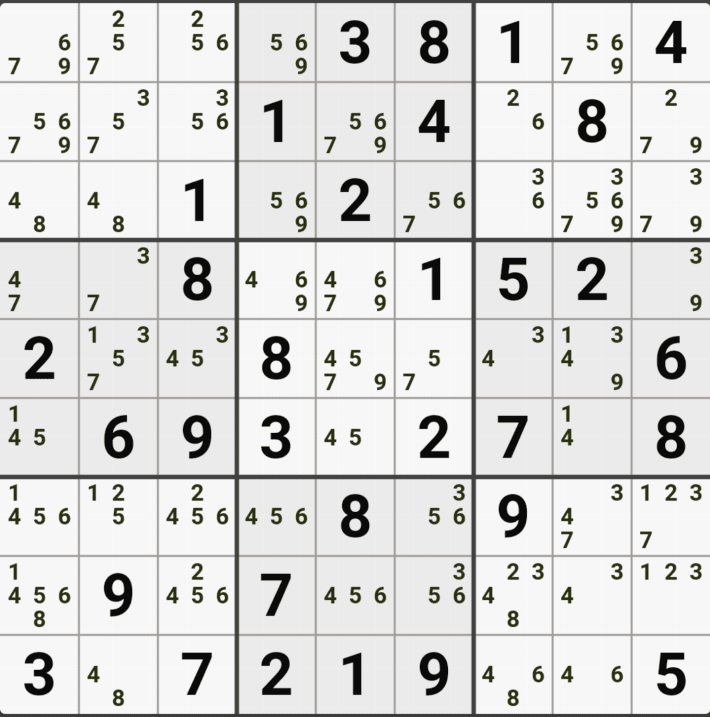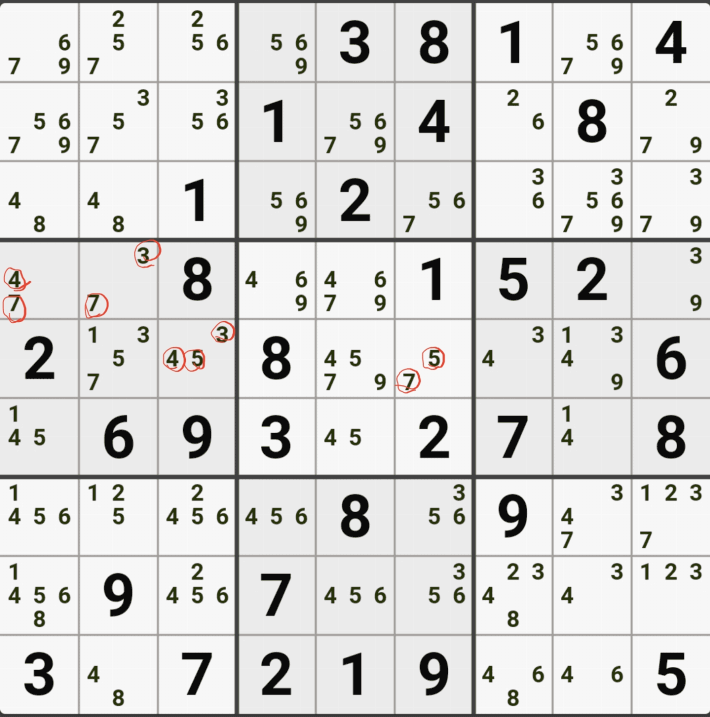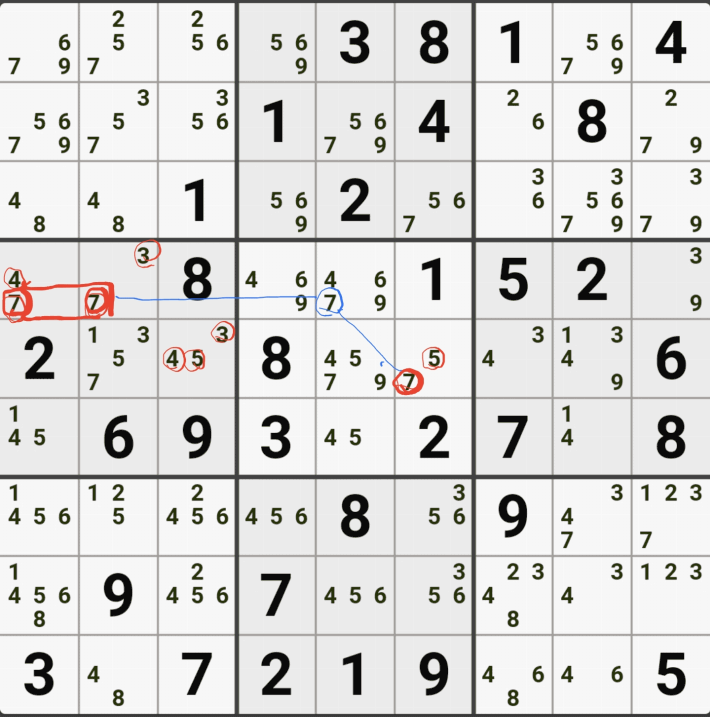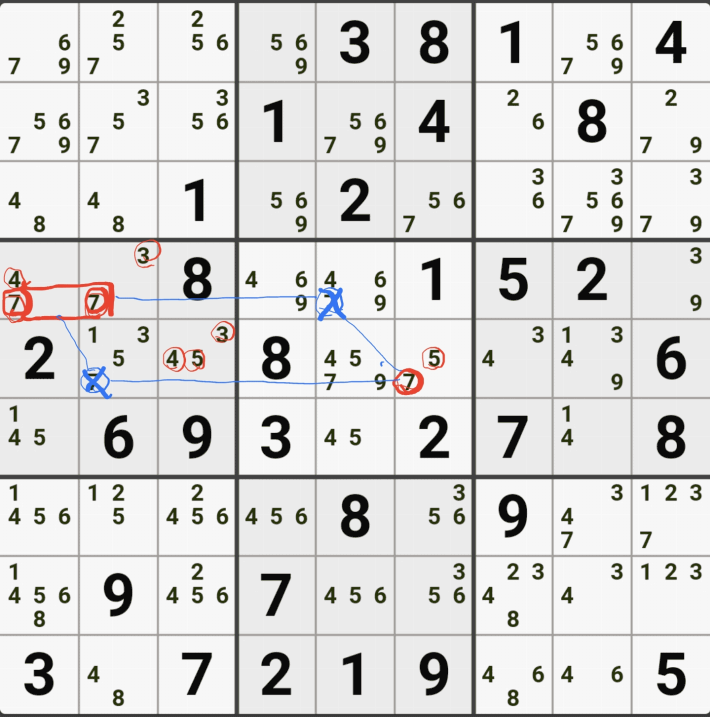
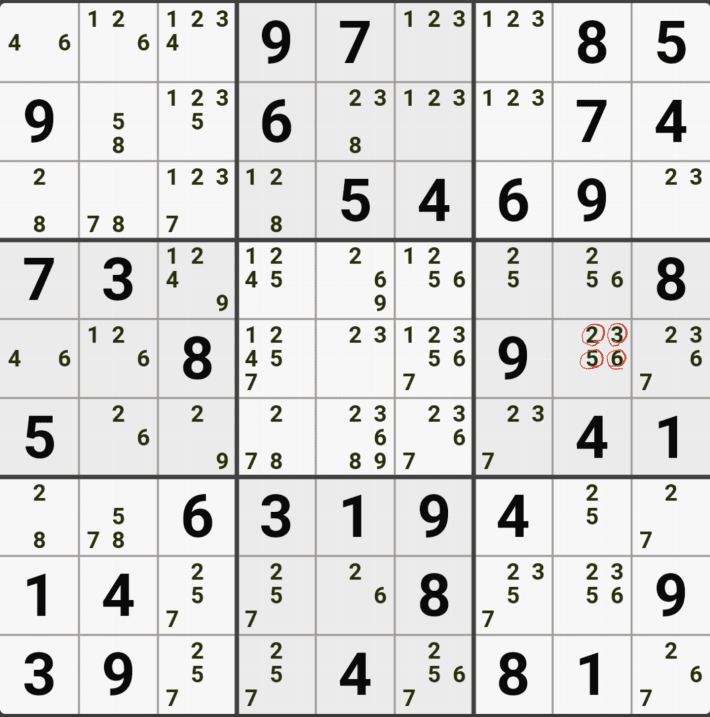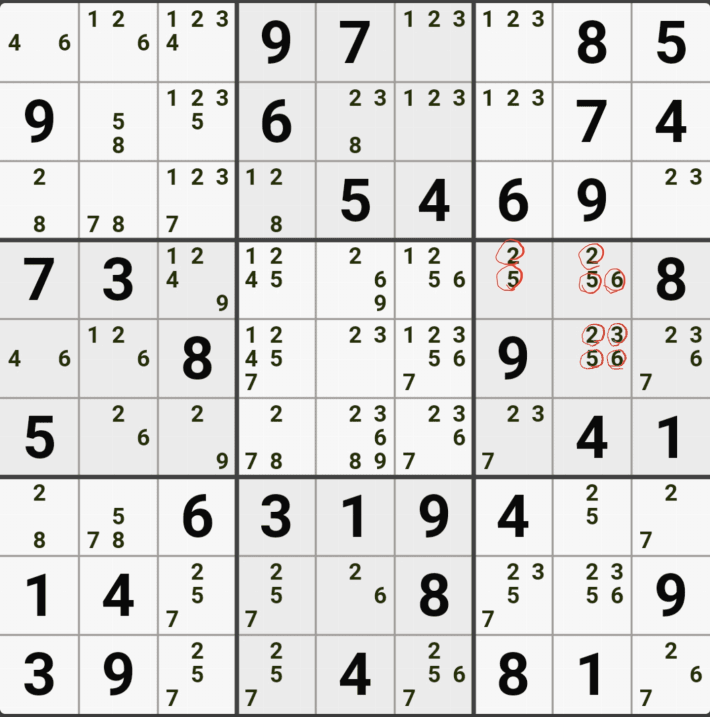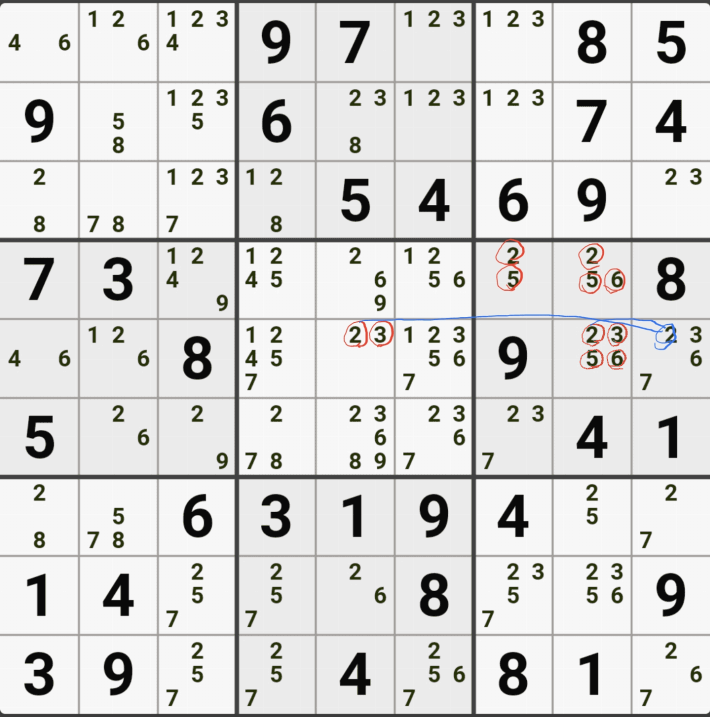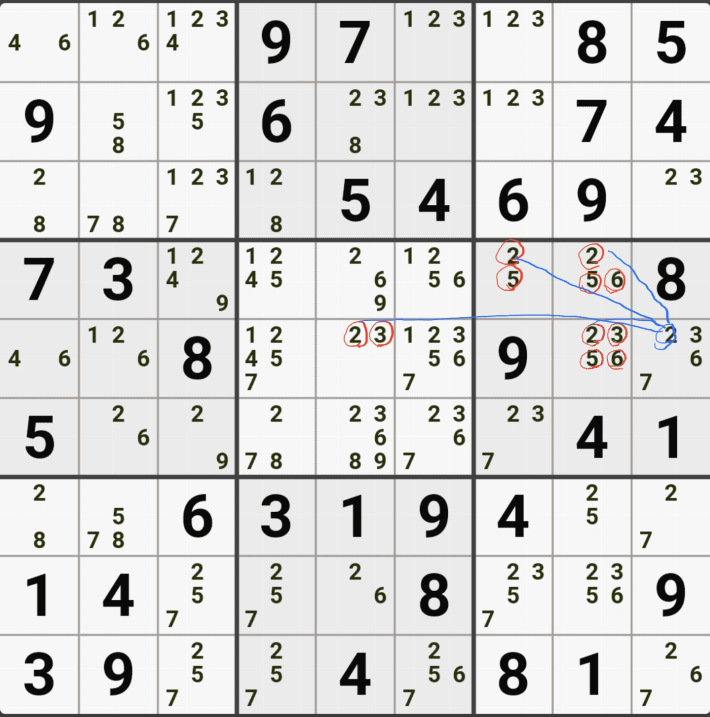
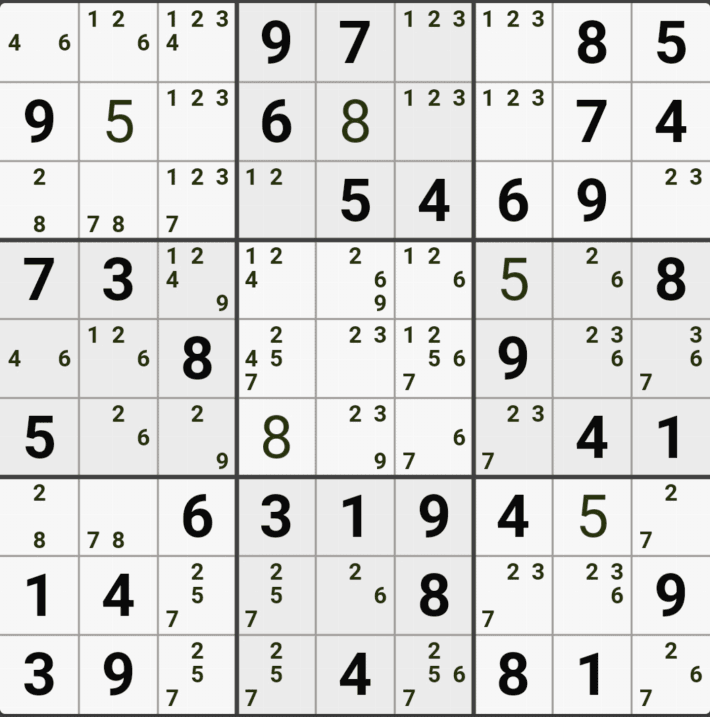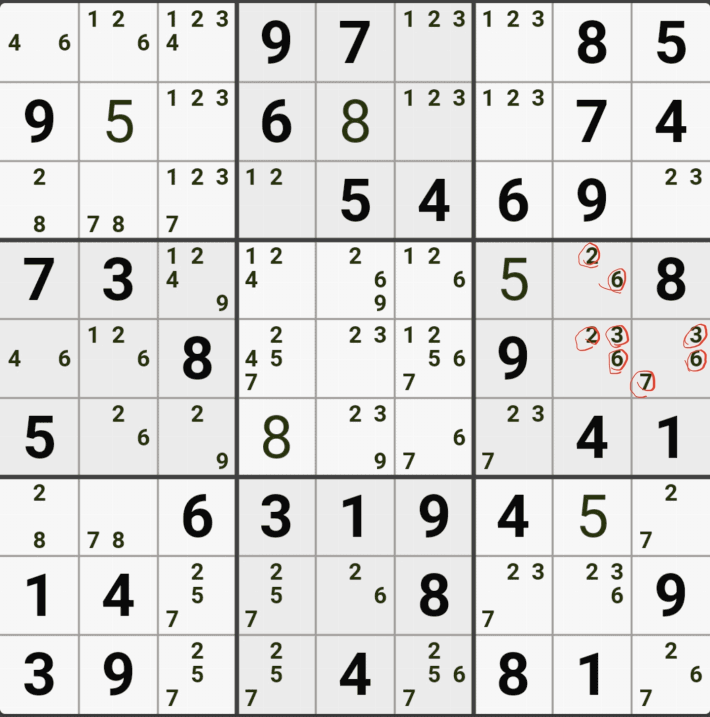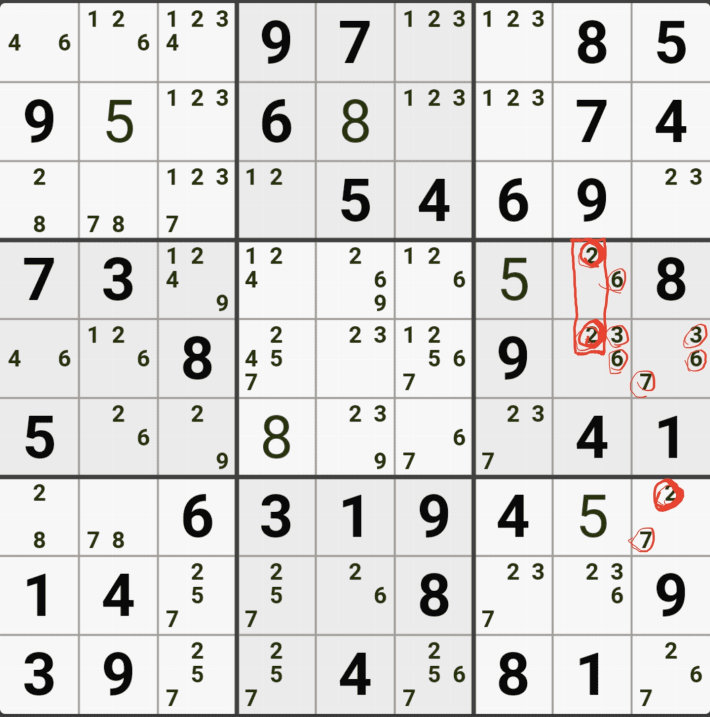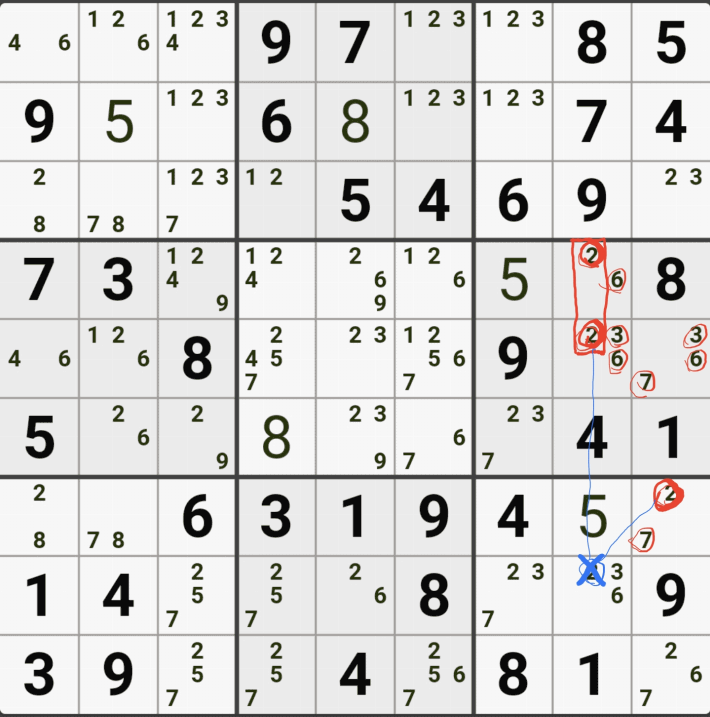
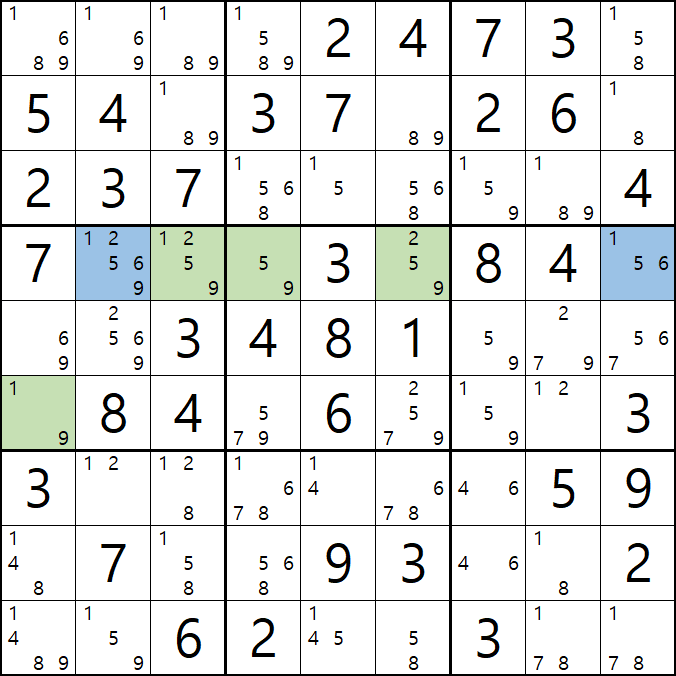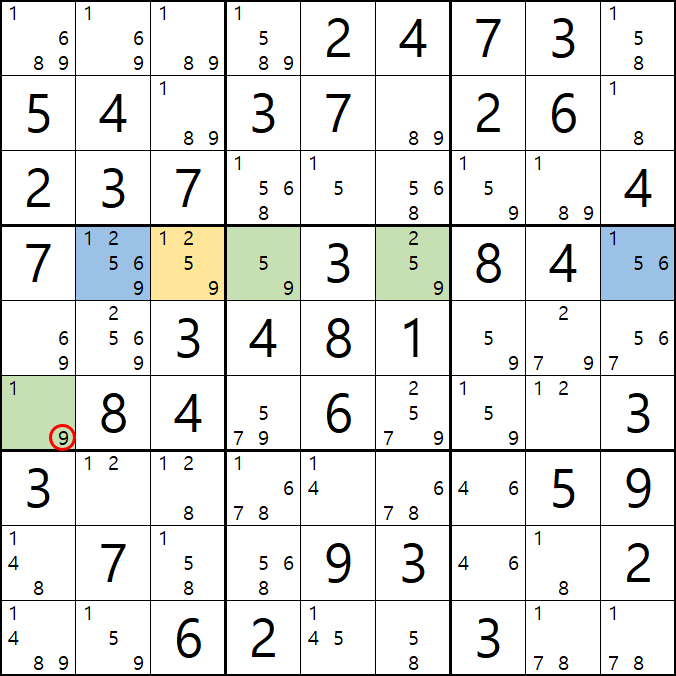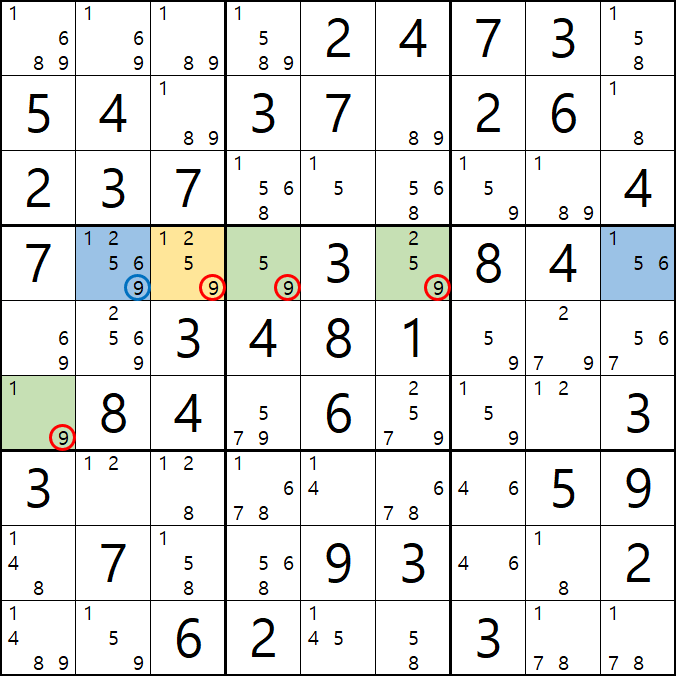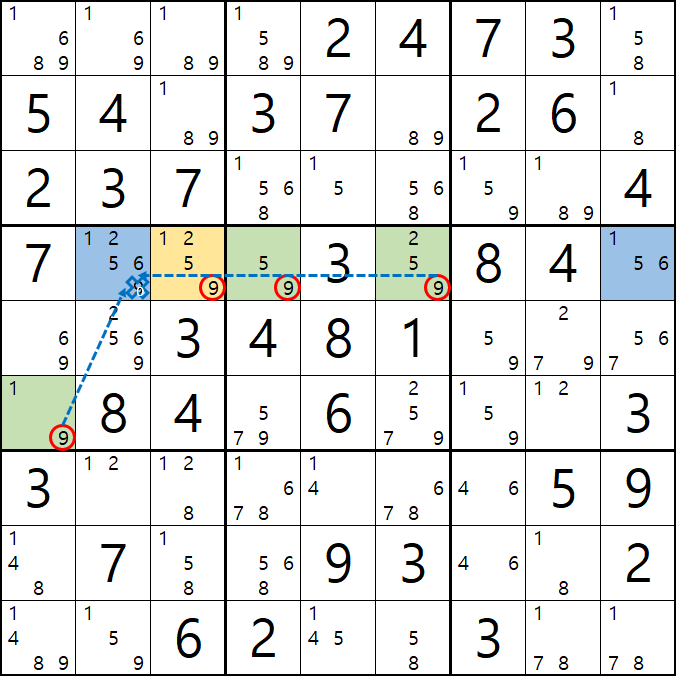
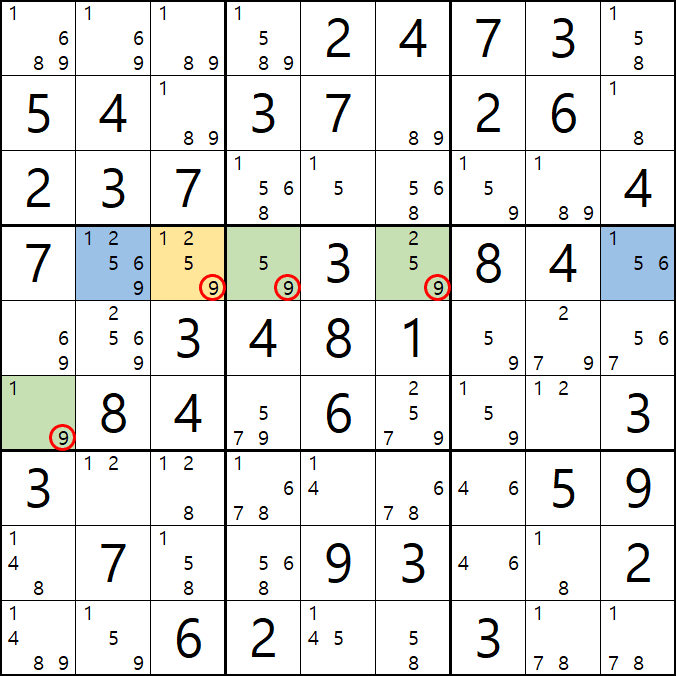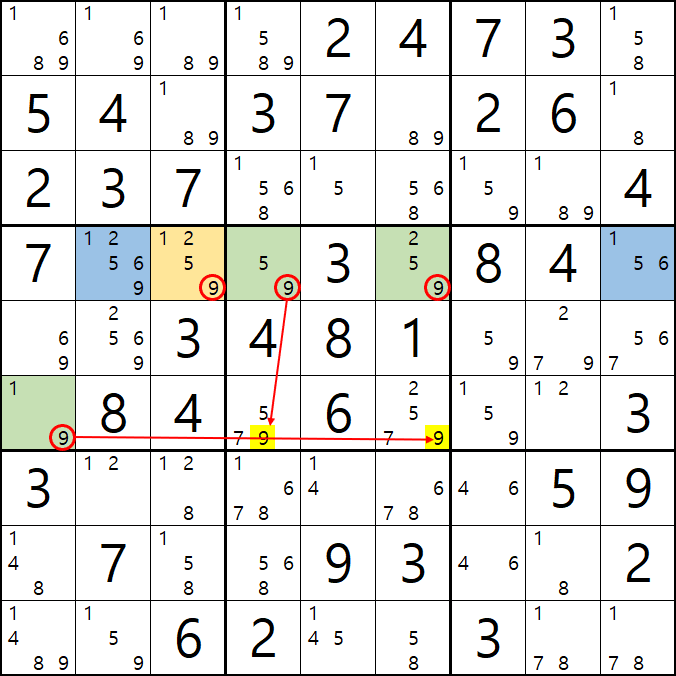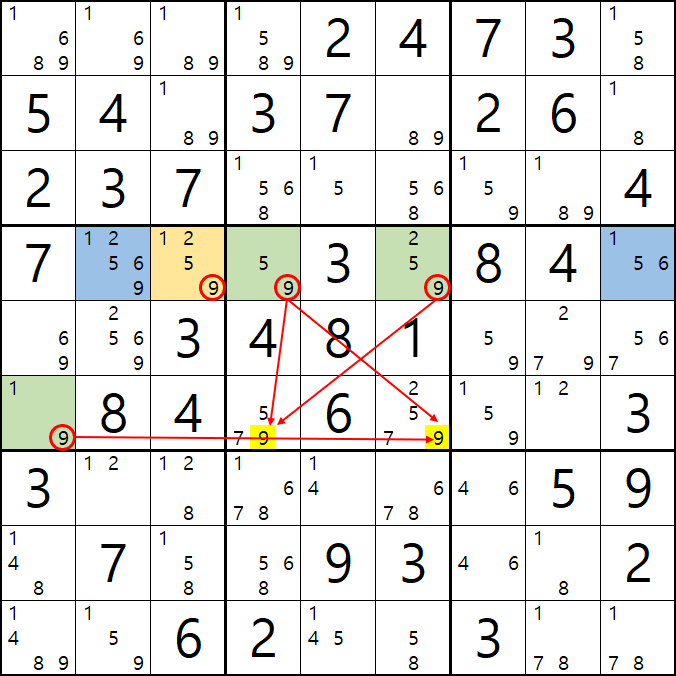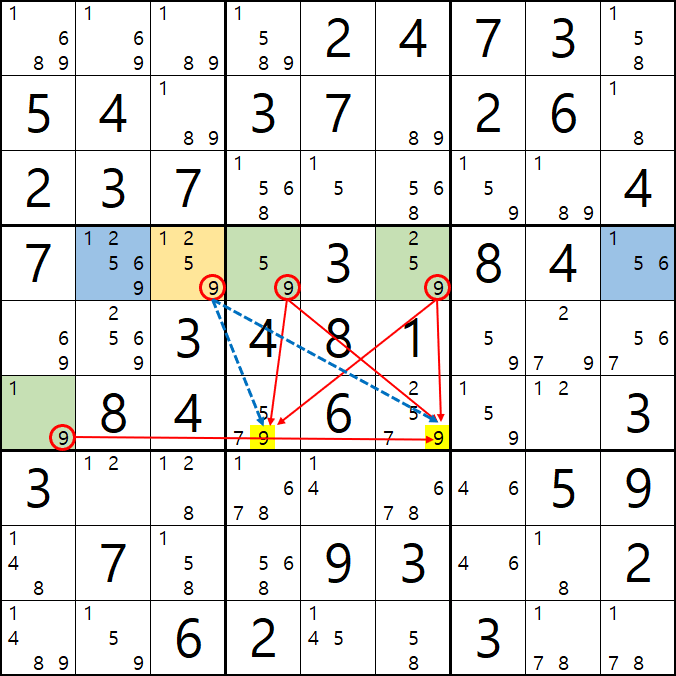
1-1. 아래와 같이 D행[D3, D4, D6]에 3칸 + 1열[F1]에 1칸, 총 4칸이 잠긴 확실한 쿼드를 이루는 것을 알 수 있다.  

 

1-2. 확실한 쿼드를 이루고 있는 구성숫자 1/2/5/9 간의 연결관계를 살펴 보면

 

1/2/5/9[D3]을 피벗으로 하는 확실한 쿼드러플이 박스4와 D열 2개의 하우스에 걸쳐서 존재하는데 

 

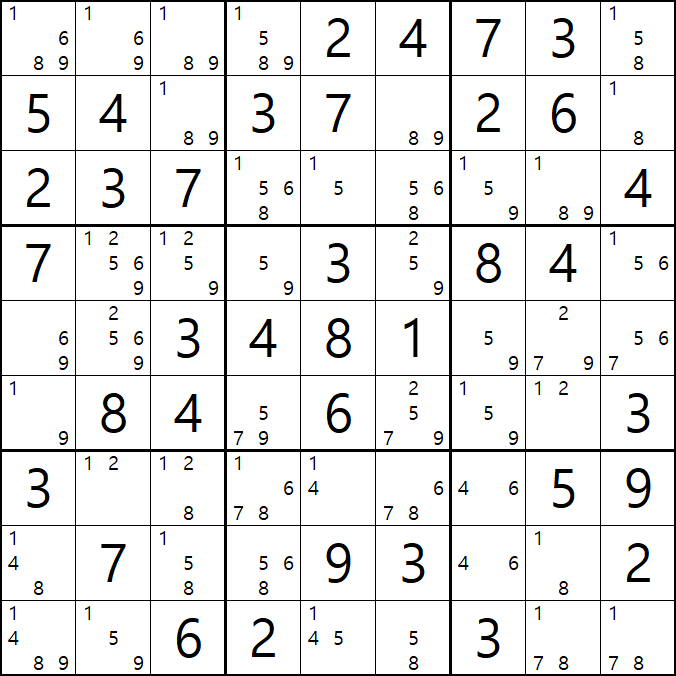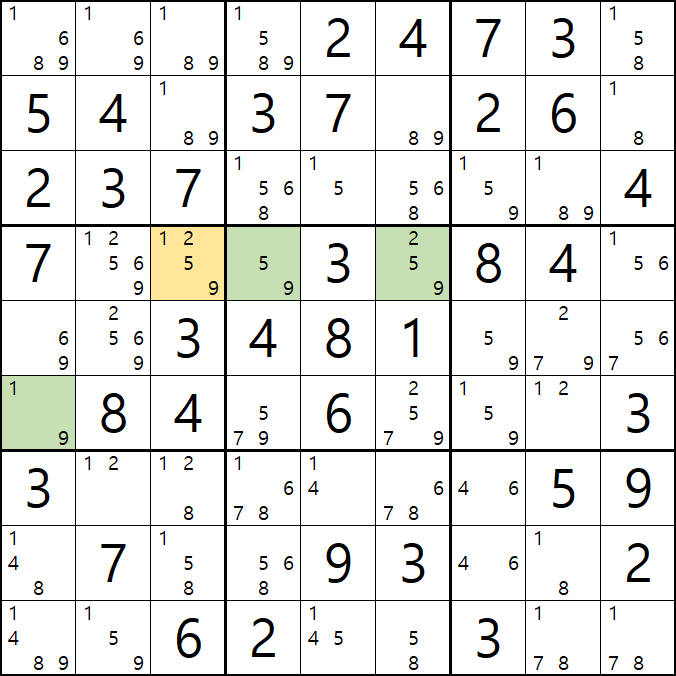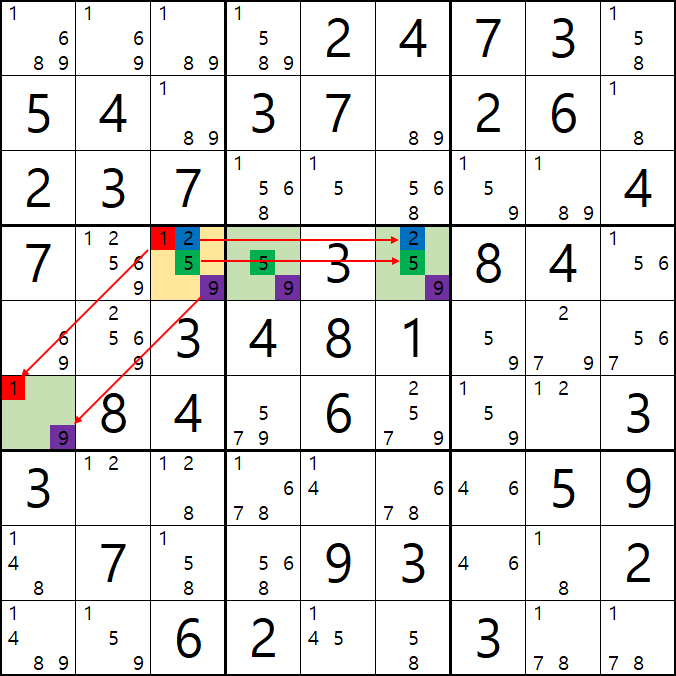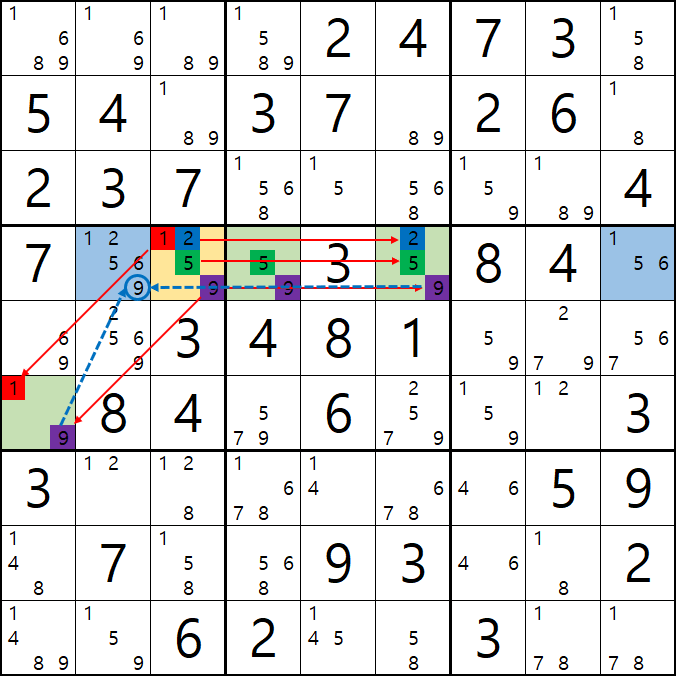
1-3. 후보숫자 1은 박스 4에만 연결이 되어 있고, 

       후보숫자 2는 D행에 대해서만 열결이 되어 있고, 

       후보숫자 5 또는 D행에 대해서만 연결이 되어 있는 것을 알 수 있다. 

 

즉, 2개의 하우스 중에 1개의 하우스에 대해서면 열결이 된 것을 알 수 있는데

 

이렇게 2개 이상의 하우스에 걸쳐 있는 2개의 칸으로 형성되는 WXYZ윙에서 1개의 하우스에만 연결(=또는 존재)되는 후보숫자를 '제한된 후보숫자'라고 한다. 

 

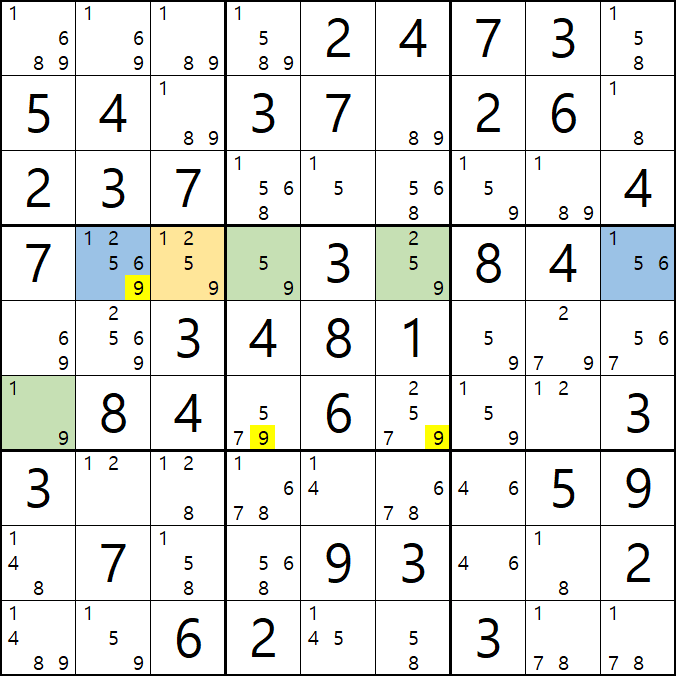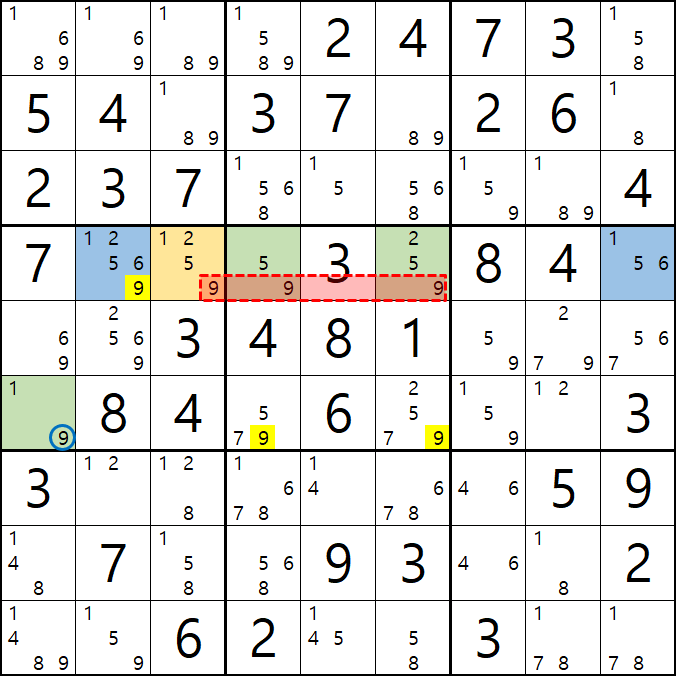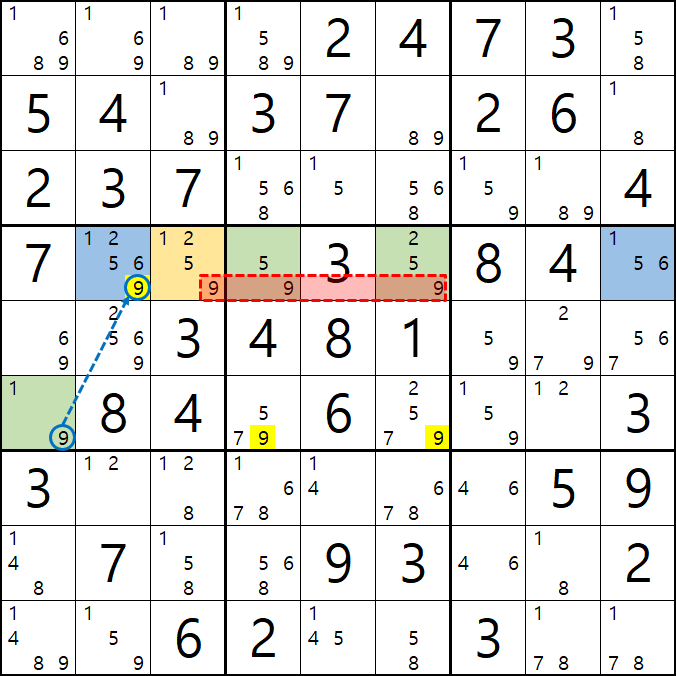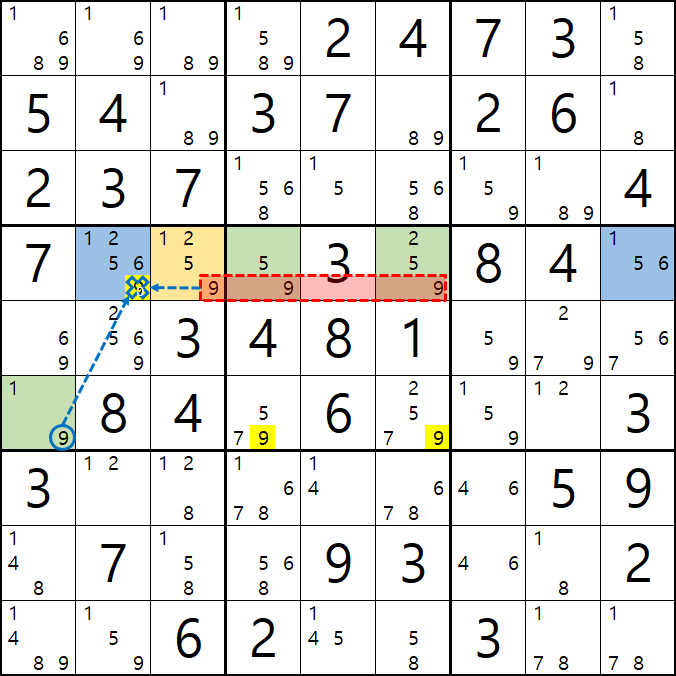
1-4. 반면에 후보숫자 9는 아래 짤과 같이 

후보숫자 9는 박스4 및 D열 모든 하우스에 걸쳐 존재하게 되는데 이런 상태의 후보숫자를 '제한되지 않은 후보숫자' 또는 '잠긴 세트'라고 부른다. 

 

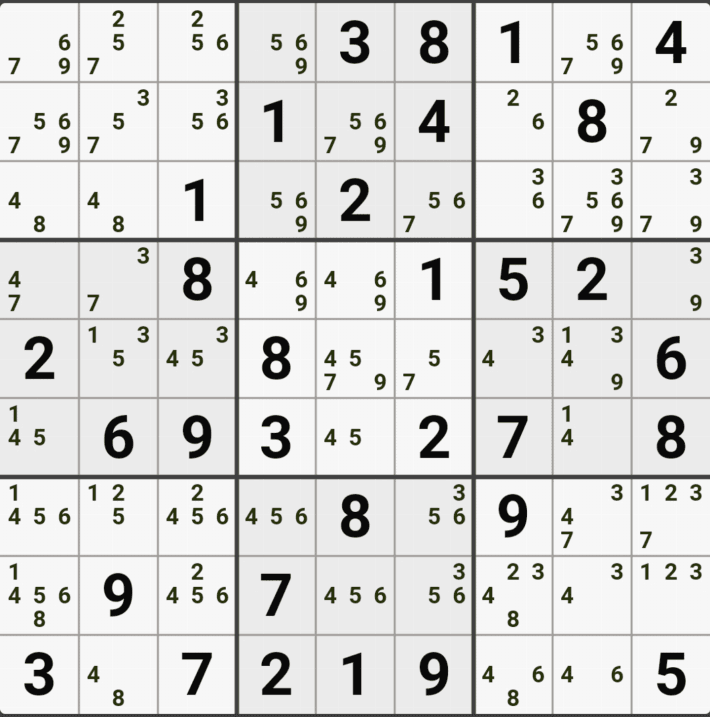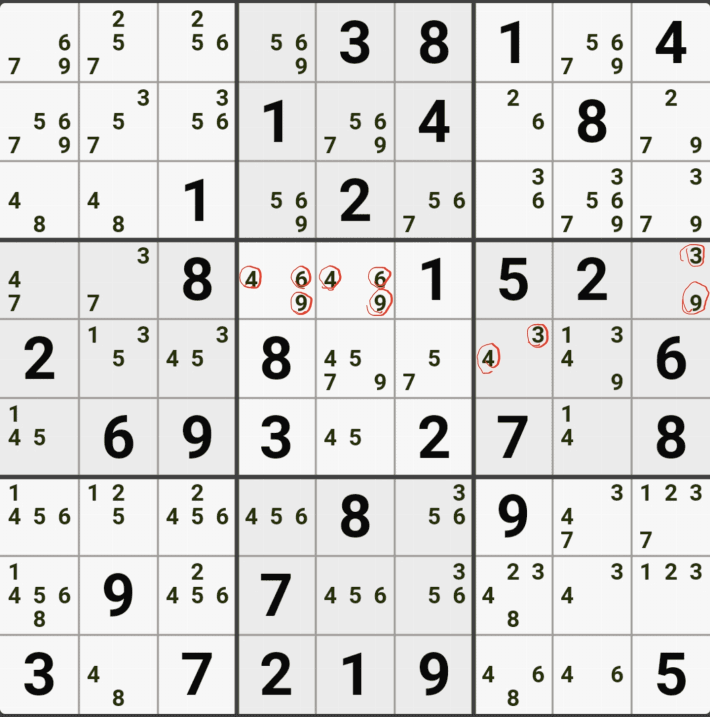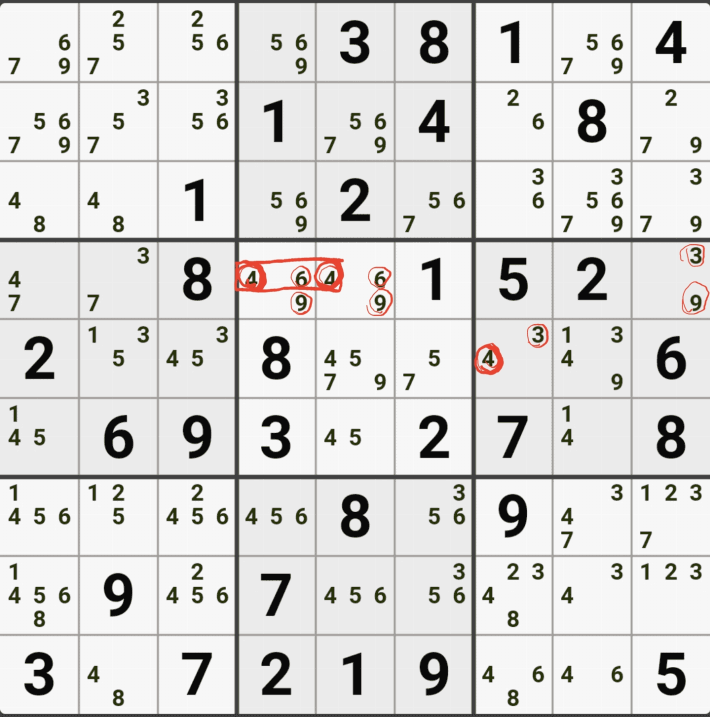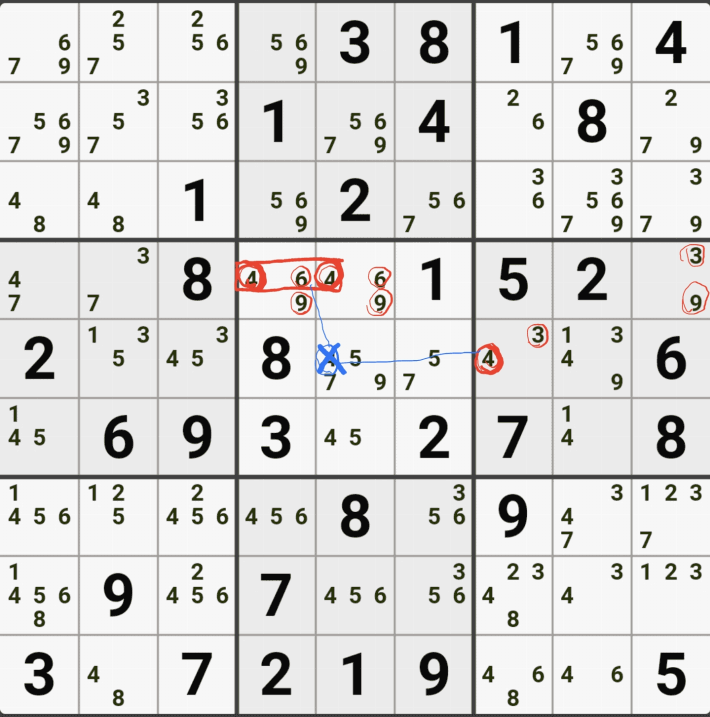
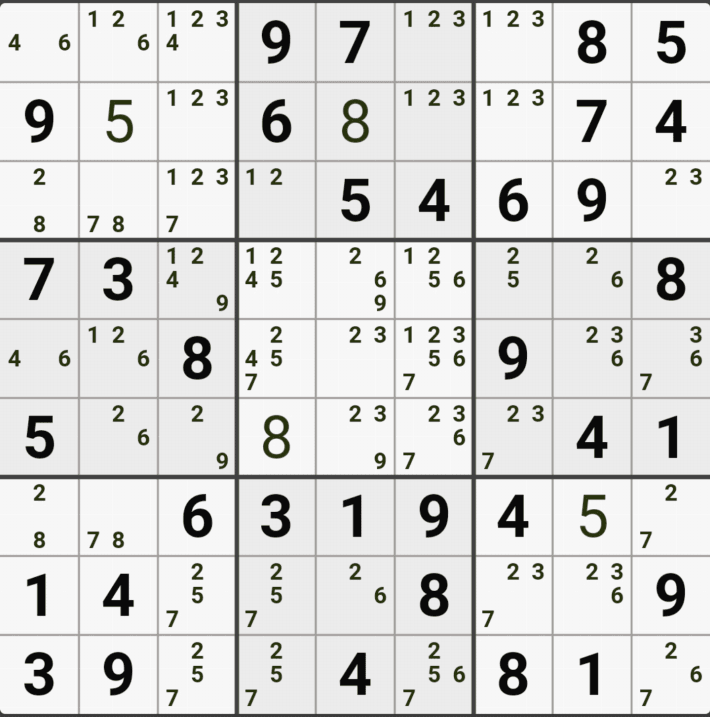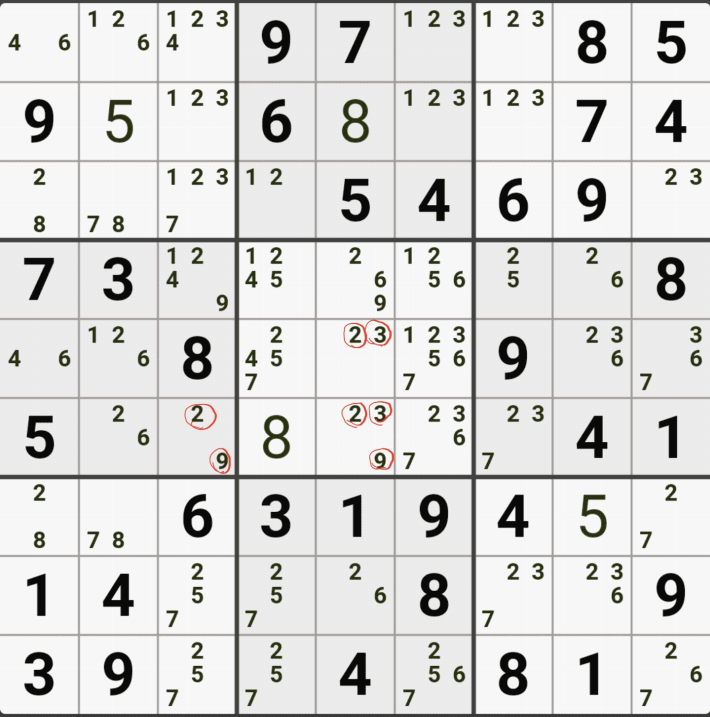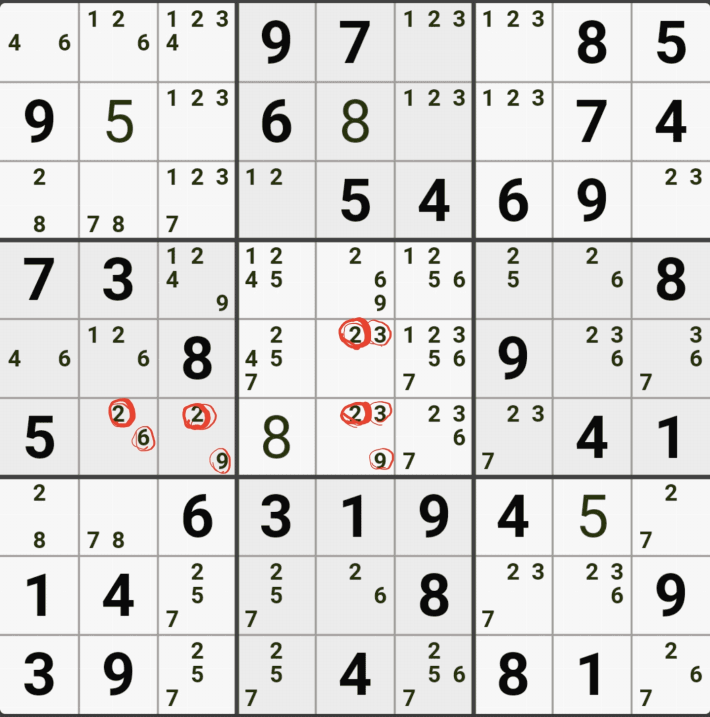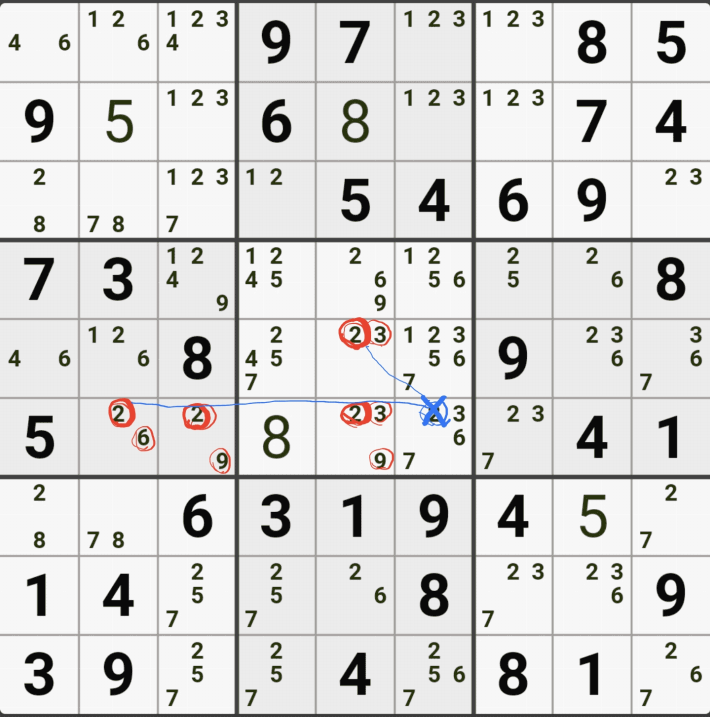
1-5. WXYZ윙을 구성하는 숫자 중에서 위와 같이 잠긴세트인 후보숫자 9 모두 동시에 바라보는 후보숫자 9[D2]는 아래 움짤과 같이 제거할 수 있다. 

 

1-6. 조금 지저분해서, 실제로 WXYZ윙 이루는 칸 및 잠긴 후보숫자를 봤을 때는 아래와 같이 암산을 하면 되겠다.

 

 

1-7. 아마 XY윙을 아는 스도커라면 박스 5에 있는 9[F4] 와 9[F6]도 지워져야 하는 거 아닌가?'라는 생각을 하겠지만 아래 움짤과 같이 9[D3]이 9[F4] 와 9[F6]과는 링크 되지 않기 때문에 제거가 불가능 하다. 

 

 그럼 WXYZ윙은 찾기도 힘들고 별거 아닌 공식이 아닐까?'라는 생각을 할 수도 있는데.... 1. 클래식한 WXYZ 이라고 제목을 붙인 이유가 있다. 후보숫자가 많기에 변초가 많은 공식이라 때문에 모든 경우를 마스터하면 유용한 공식 맞다.  

 

2. 피벗에 WXYZ 중에 후보숫자가 한개가 빠진 WXY, WXZ, WYZ인 경우.

 

2-1. 

만약 위에서 본 움짤 예제중 1-7.과 같은 아래의 그림 상황에서 9[D2] 뿐만 아니라

F행에 있는 9[F4], 9[F6]을 지울 수 있는 상황이 될 순 없을까?

 

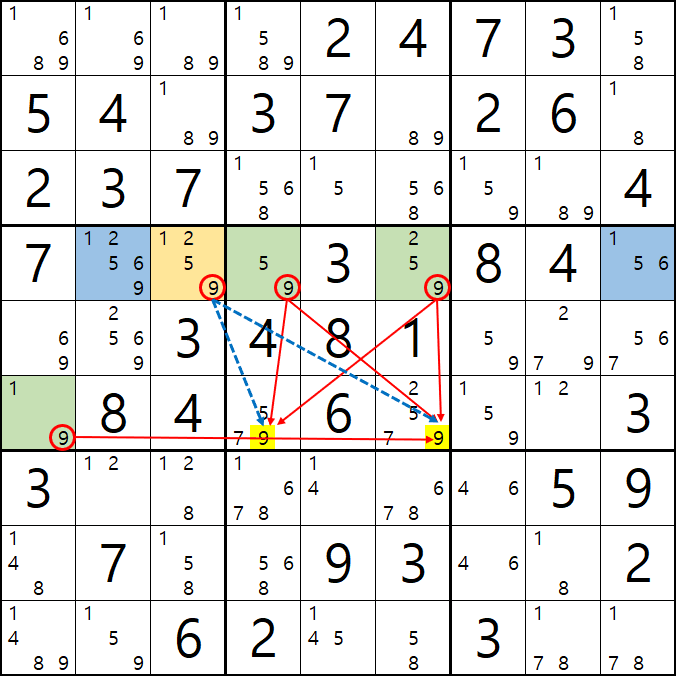
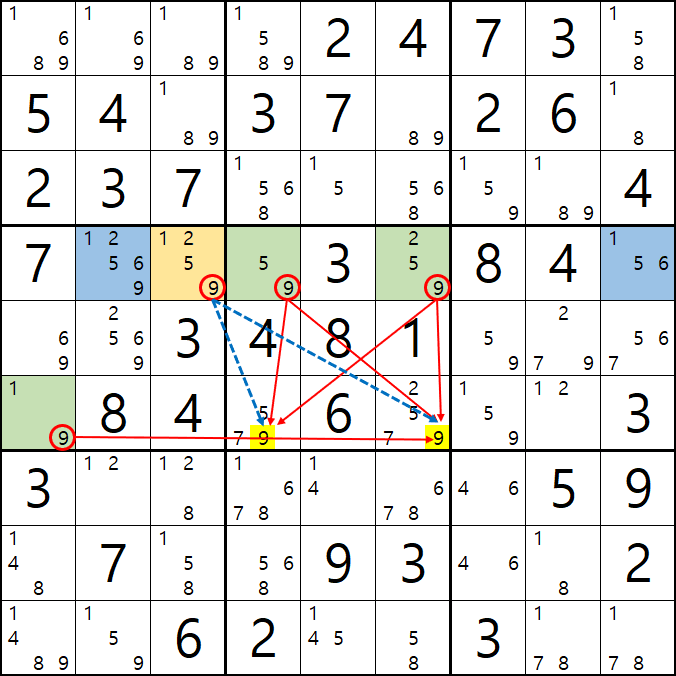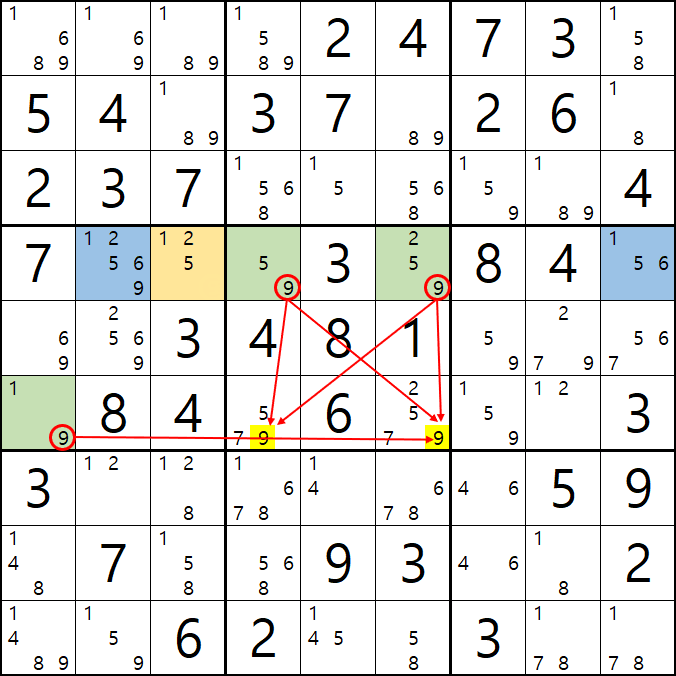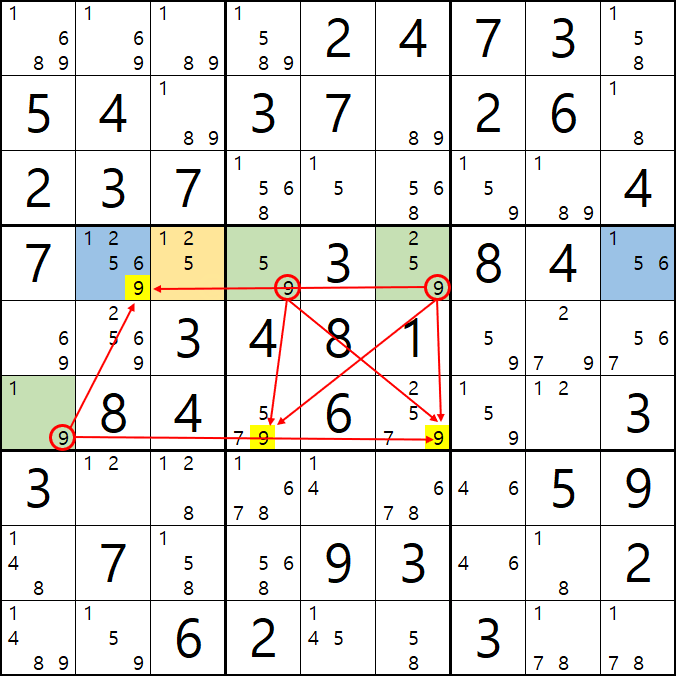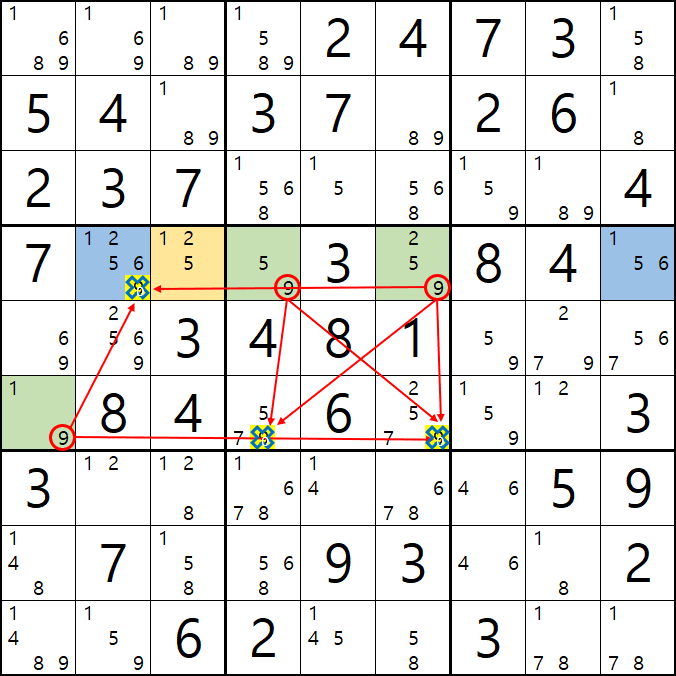
당연히 있다. 9[D3]을 아래 움짤과 같이 제거해 주면 된다. 아래 움짤처럼 9[D3]를 제거하더라도 

19 / 125 / 59 / 259로 확실한 쿼드러플을 이루는 것을 알 수 있다.

 

 

으아니 그런데, 이렇게 화살표만 늘어가면 눈과 머리가 복잡해 진다. 그래서 WXYZ윙을 볼 때는 그룹 링크 개념으로 보자. 위의 1. 2번 예제를 그룹 링크로 정리하면 아래와 같다. 

 

1. 클래식한 WXYZ을 그룹 링크로 엮었을 때...

 

 

2. 피벗이  WXY, WXZ, WYZ인 경우를 그룹 링크로 엮었을 때...

 

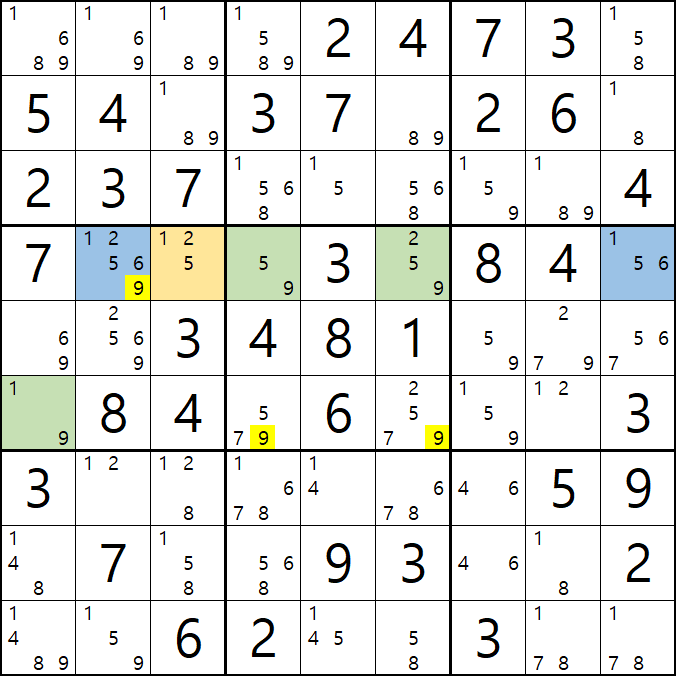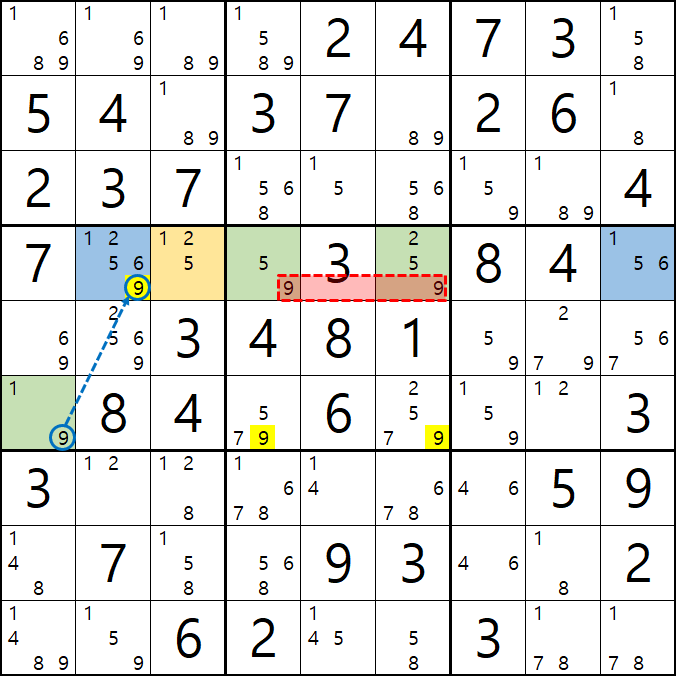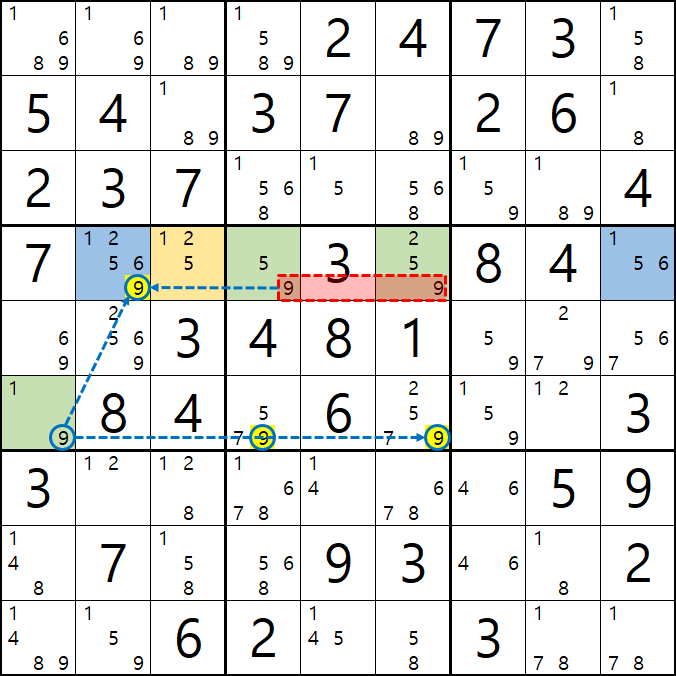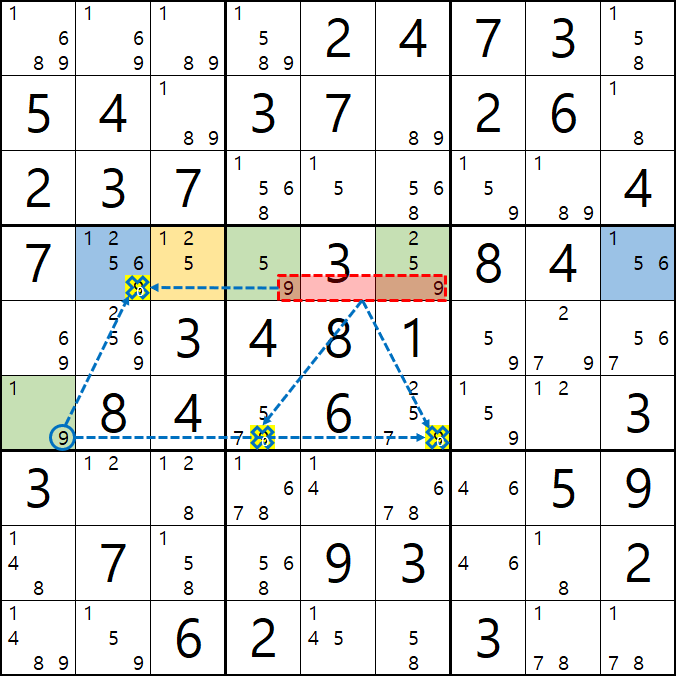
그룹 링크는 정말 상상하는대로 스도쿠에 적용할 수 있다. 아래 그룹 링크에 대한 글을 읽어 보기를 권한다. 

스도쿠 20. 고급공식/ 그룹 링크 X 사이클 공식-움짤, 패턴

스도쿠 20. 고급공식/ 그룹 링크 X 사이클 공식-움짤, 패턴

 

2-2. 복습 차원에서 피벗이 3개의 후보숫자로 이뤄진 움짤 예제 1개만 더 보고 넘어 가겠다. 

 

 

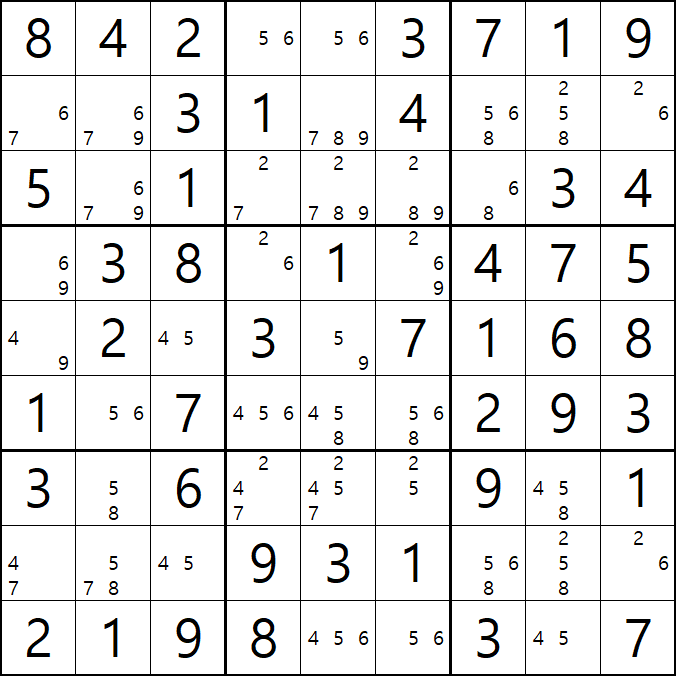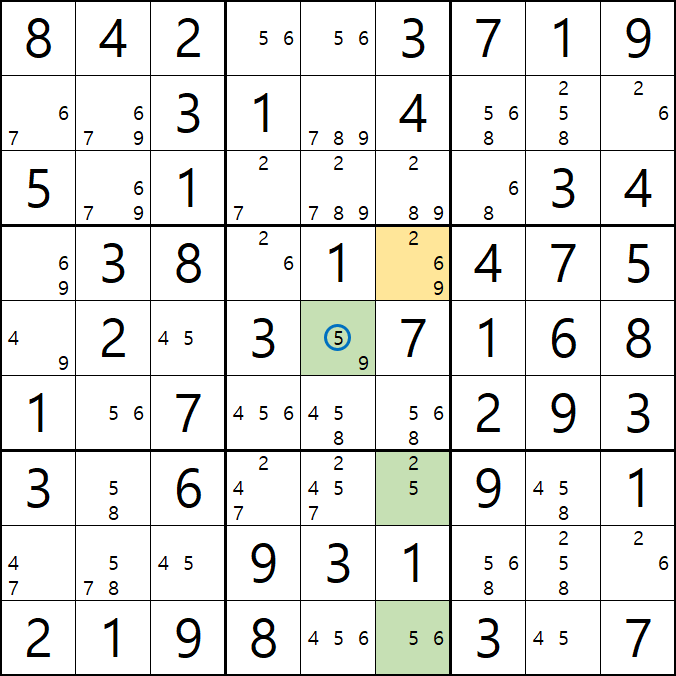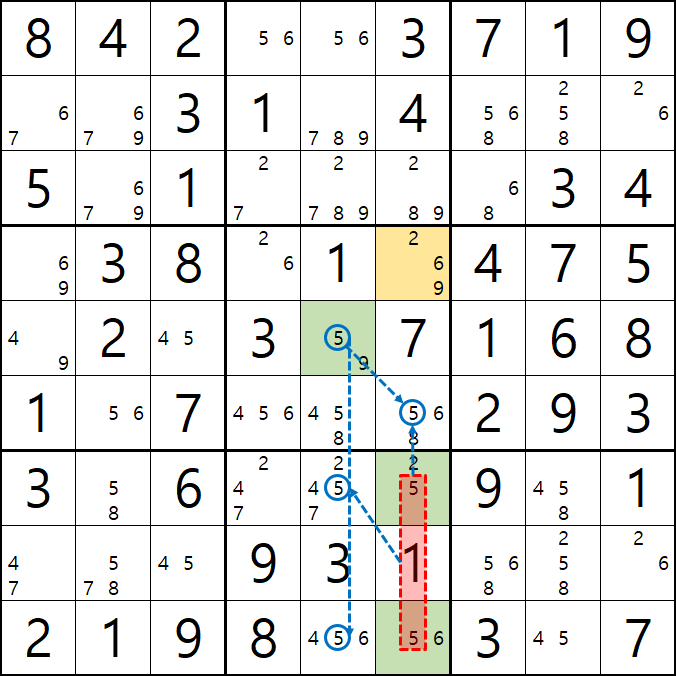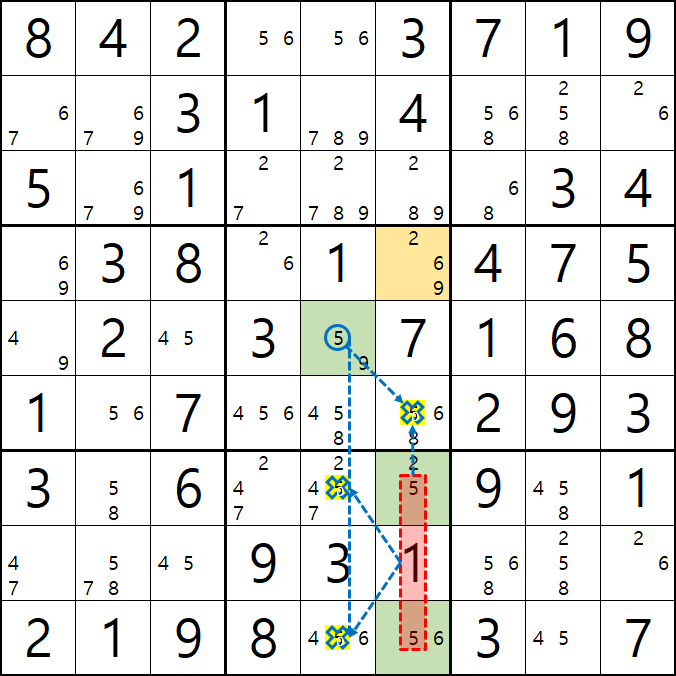
위의 움짤과 같이 2/6/9[D6]을 피벗으로 하는 5/9[E5], 2/5[G5], 5/6[I5]의 확실한 쿼드러플이 있을 때, 

박스 5와 박스7을 동시에 볼수 있는 잠긴 세트인 5[E5]와 5[G5&I5]가 동시에 보는

5[F6], 5[G5], 5[I5] 후보숫자 3개를 제거할 수 있다. 

 

지금까지는 박스 1에 쿼드러플을 이루는 칸이 2칸, 박스 2에 2칸씩 들어가는 예를 봤는데(피벗1, 핀1, 핀2)

이번에는 박스1에 피벗 포함 3칸, 박스2에 1칸이 쿼드러플을 이루는 사례(피벗2, 핀1, 핀2) 에 대해 알아보도록 하겠다. 

 

3. 피벗 2(XYZ, YZ), 핀1, 핀1 인 경우

 

 

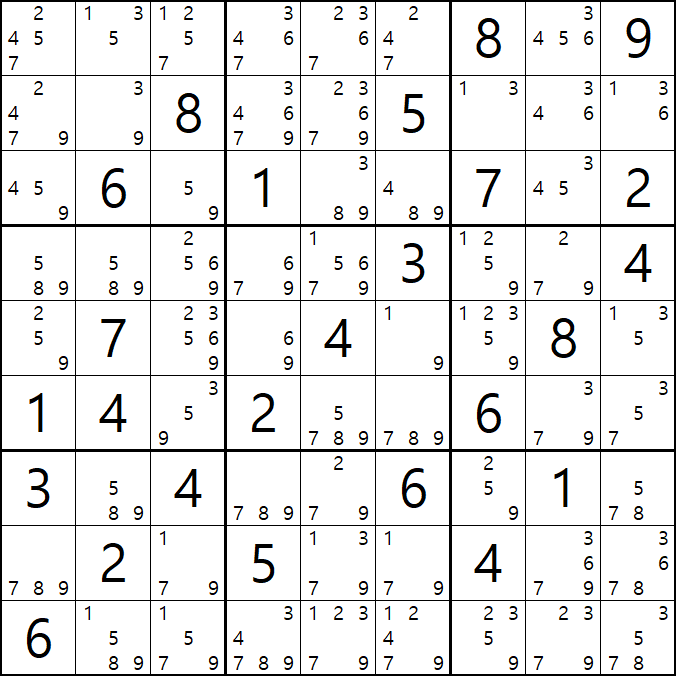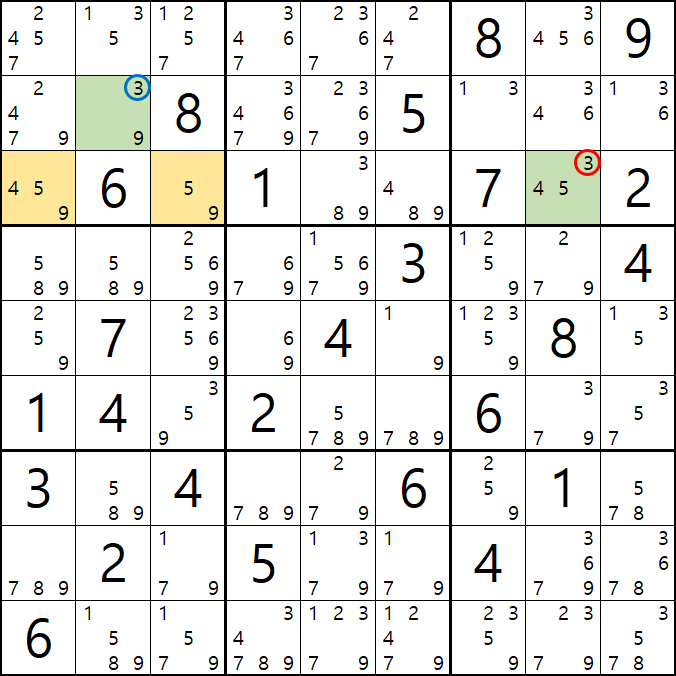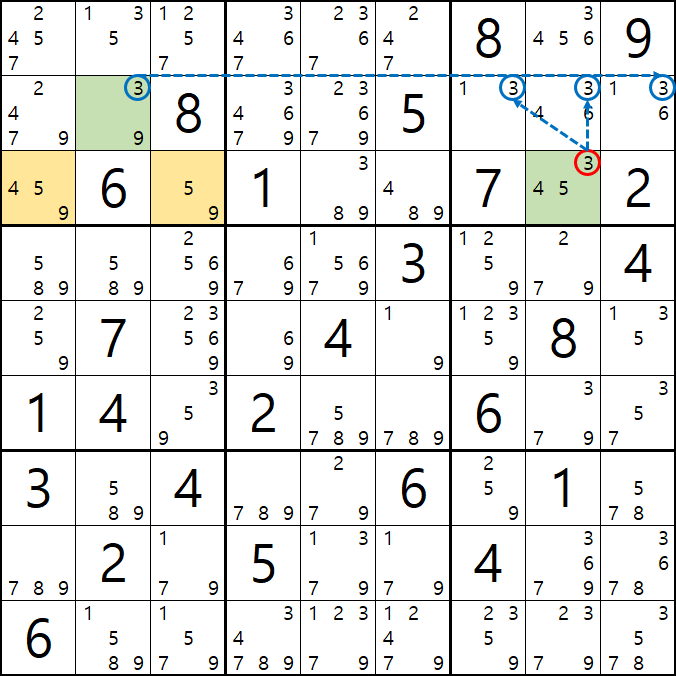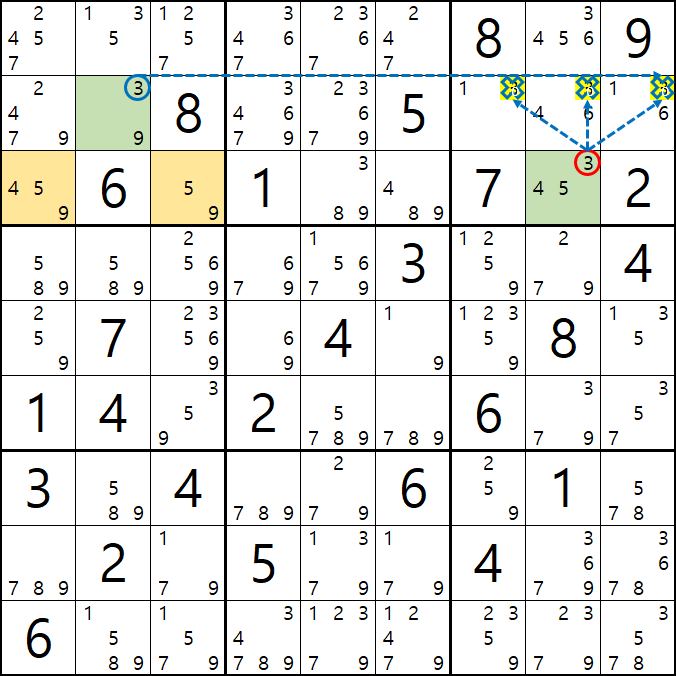
위의 움짤과 같이 4/5/9[C1] 및 5/9[C3] 을 피벗으로 하는 3/9[B2], 3/4/5[C8]의 확실한 쿼드러플이 있을 때, 

박스 1과 박스3을 동시에 볼수 있는 잠긴 세트인 3[B2]와 3[C8]이 동시에 보는

3[B7], 3[B8], 3[B9] 후보숫자 3개를 제거할 수 있다. 

 

 쿼드러플을 이루는 4칸의 후보숫자가 줄어 들 수록 좀 더 직관적이고 편하게 다른 칸의 후보숫자를 제거할 수 있는 것을 알 수 있다. 

 

이번 경우는 체인으로 움짤 증명이 가능하다. 

 

움짤 증명 1. B3이 3이라면

 

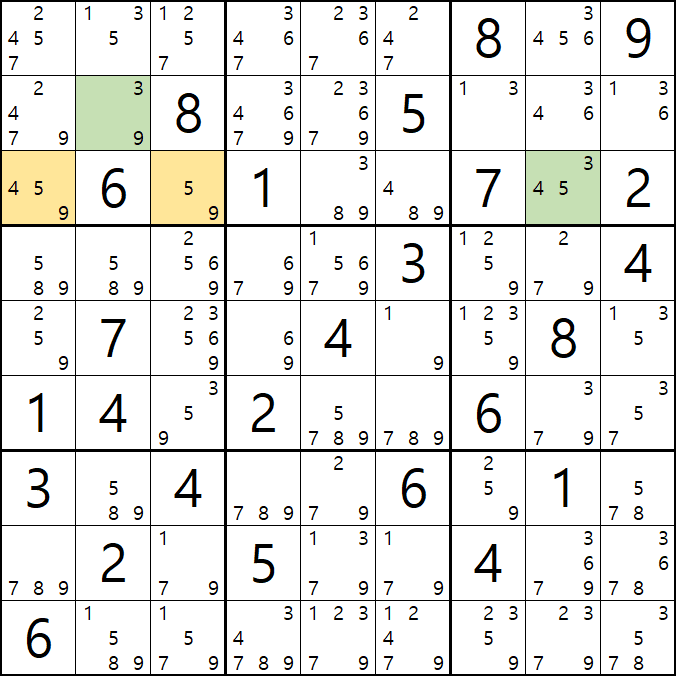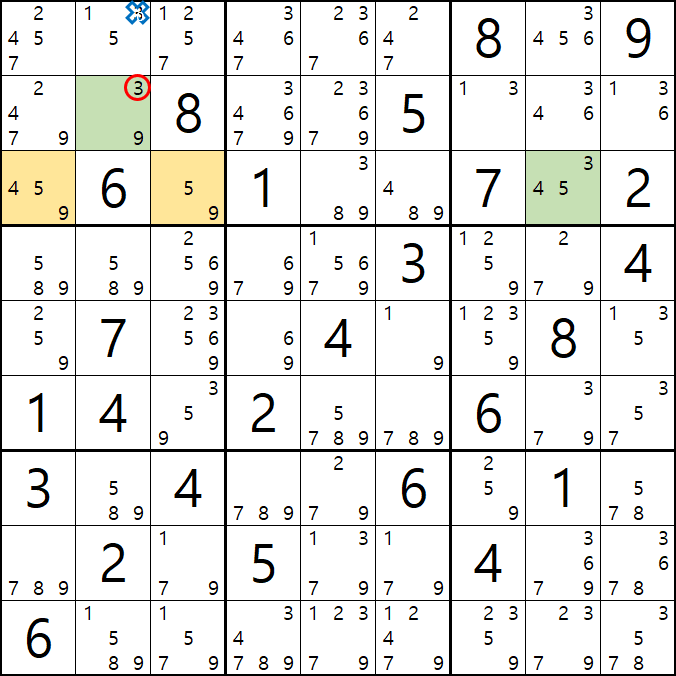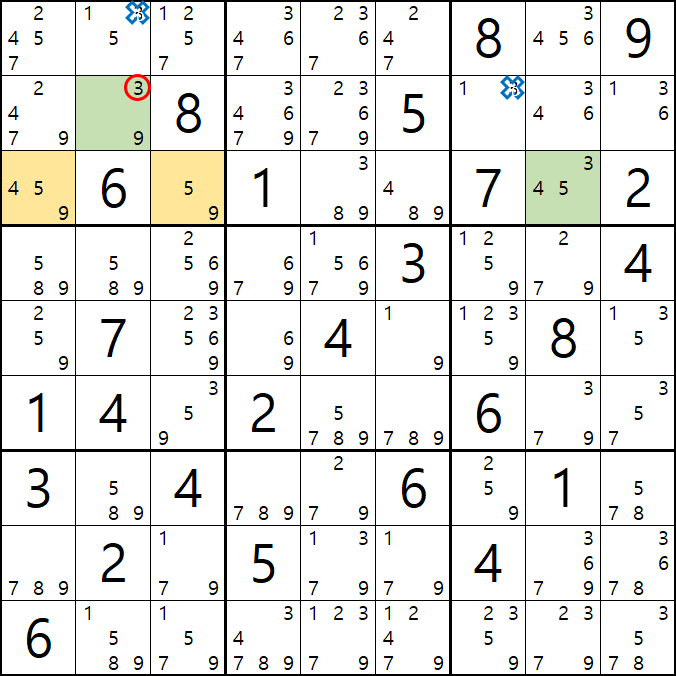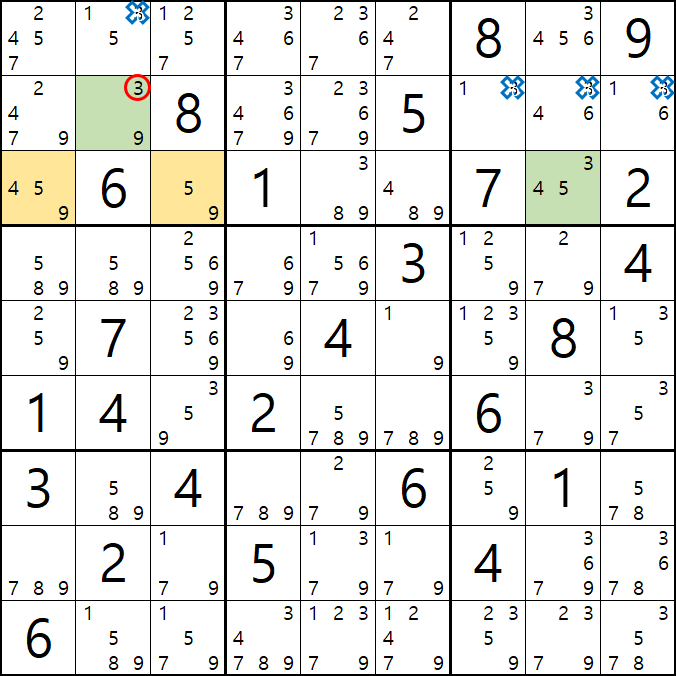
움짤 증명 2. B3이 3이 아니라면 (즉, 9라면) XY 윙의 형태가 되는 것을 알 수 있다. 

   

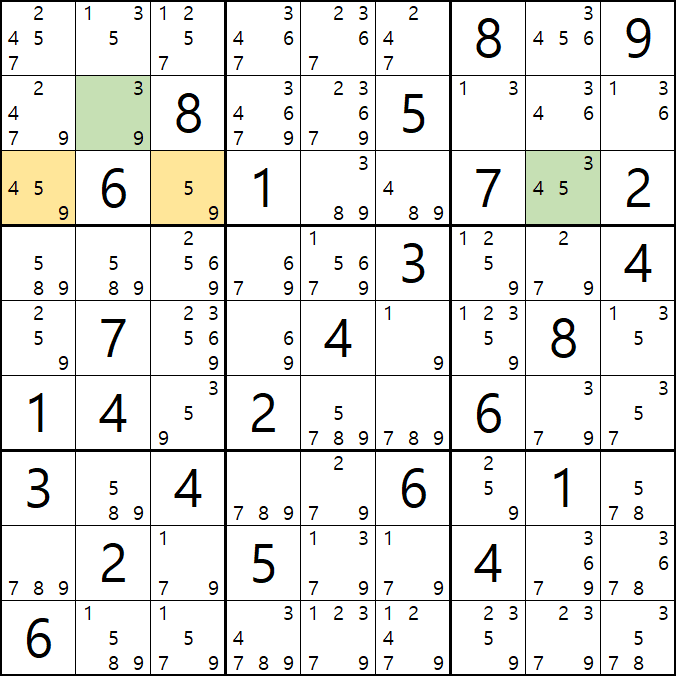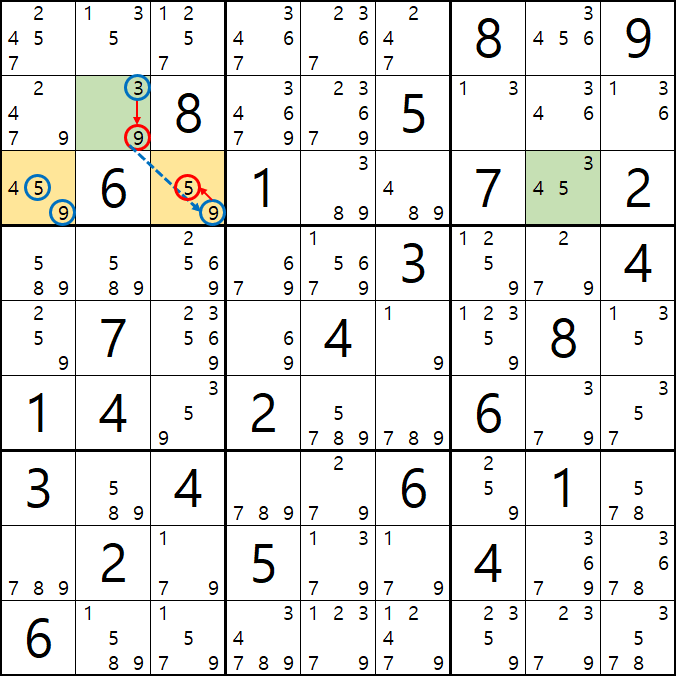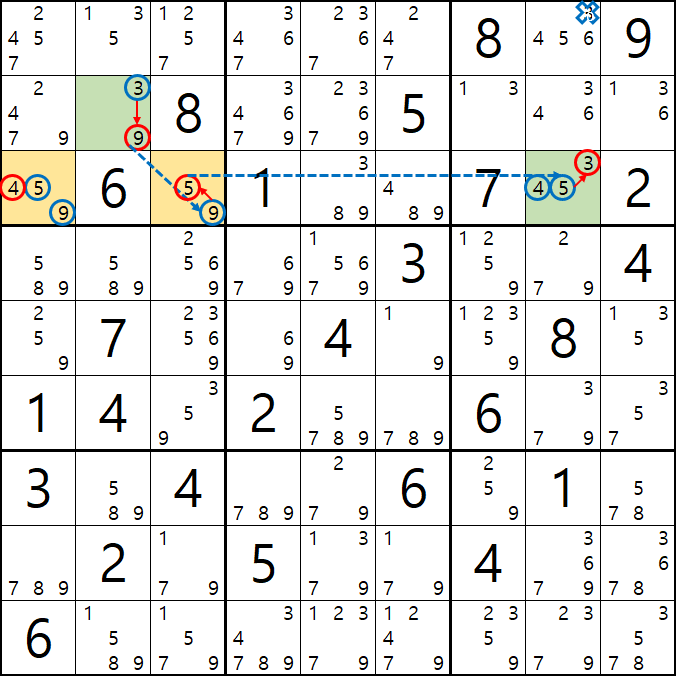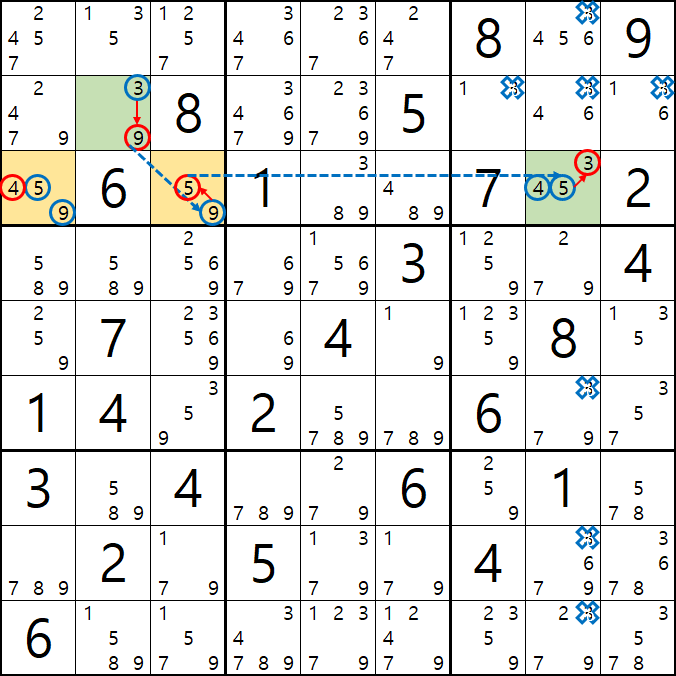
움짤 증명 3. 위의 증명 1,2의 결과에 따라 어느 경우던지 변하지 않고 동일하게 제거 되는 3[B7], 3[B8], 3[B9]를 제거할 수 있다. 

 

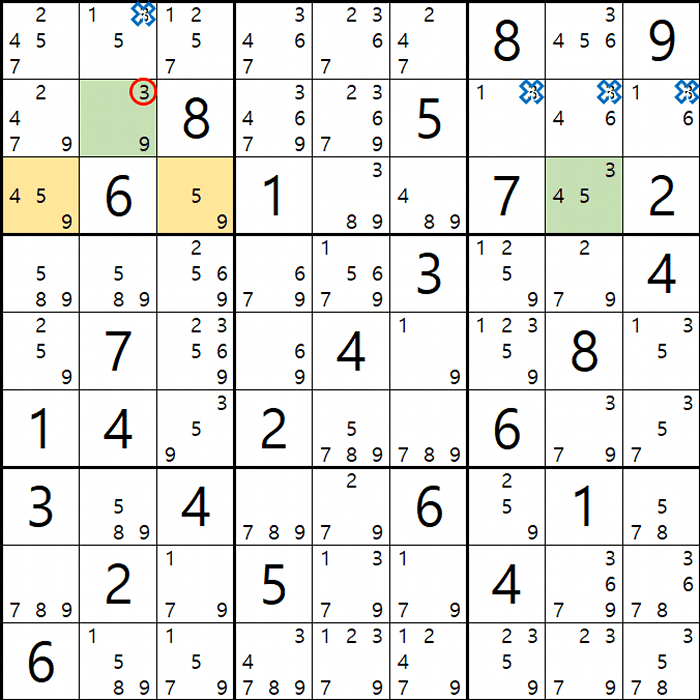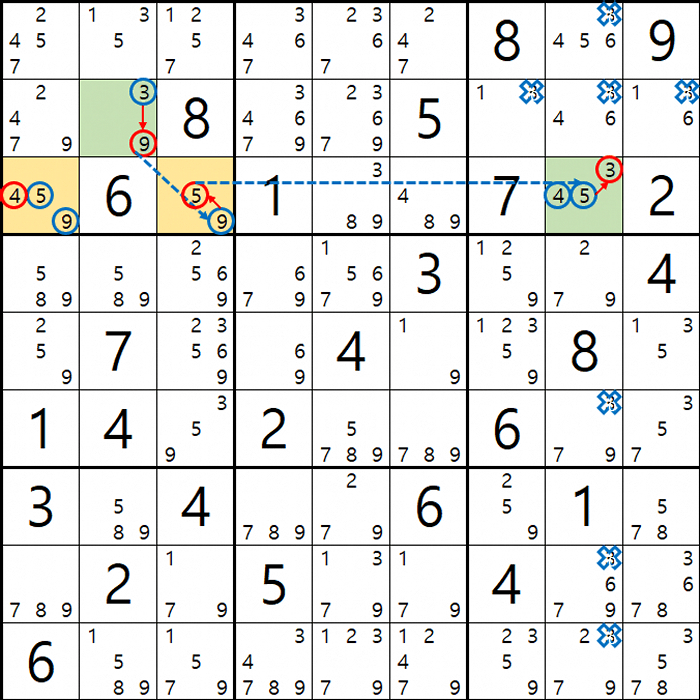
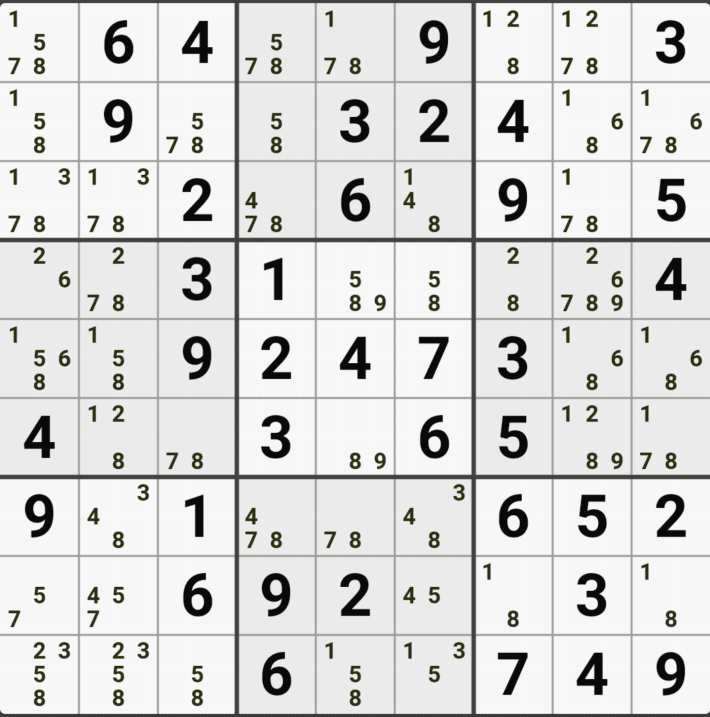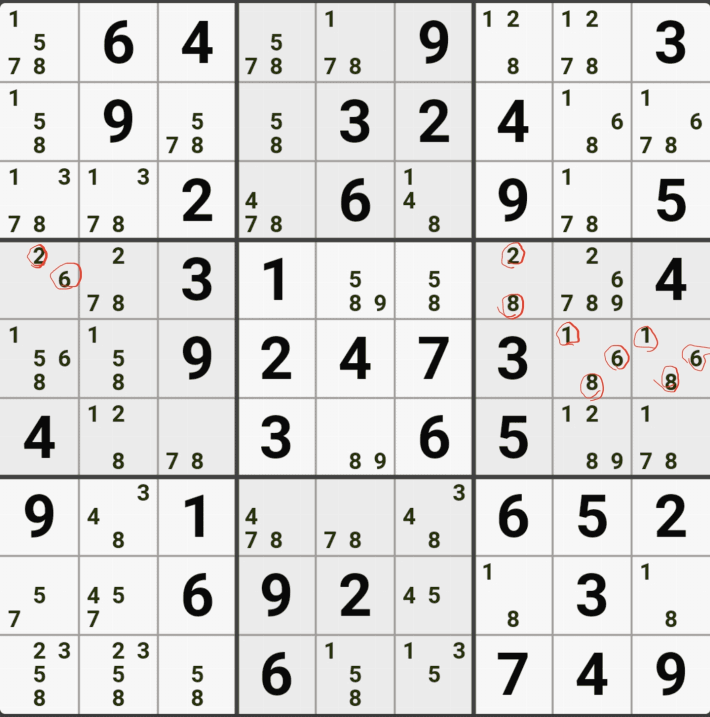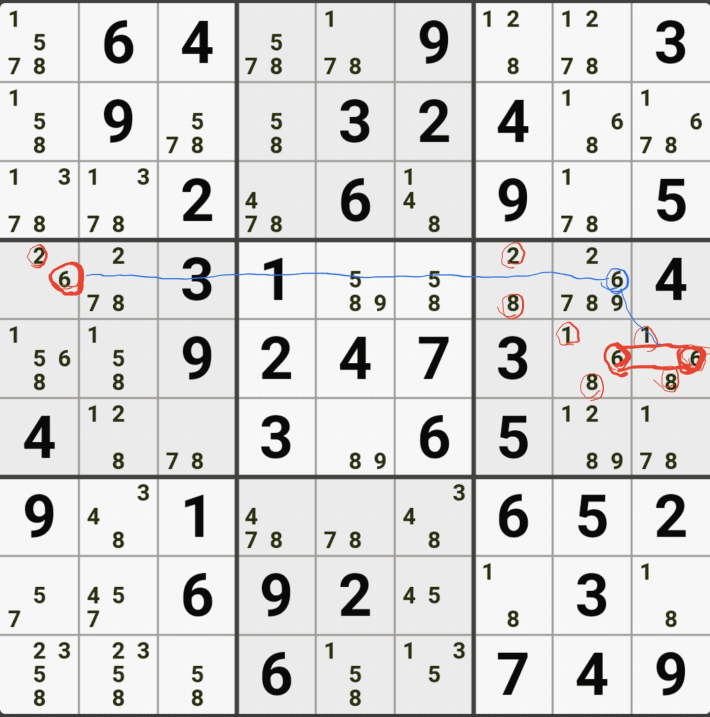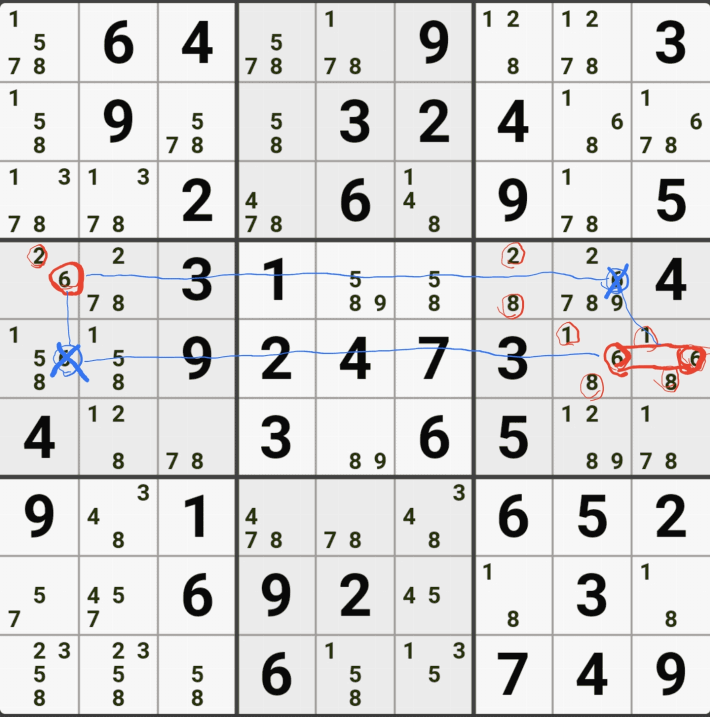
4. 피벗 1(WX, WY, WZ, XY, XZ, YZ), 핀1, 핀2(XYZ, XYZ 동일한)인 경우 (원리는 같다.)

 

 

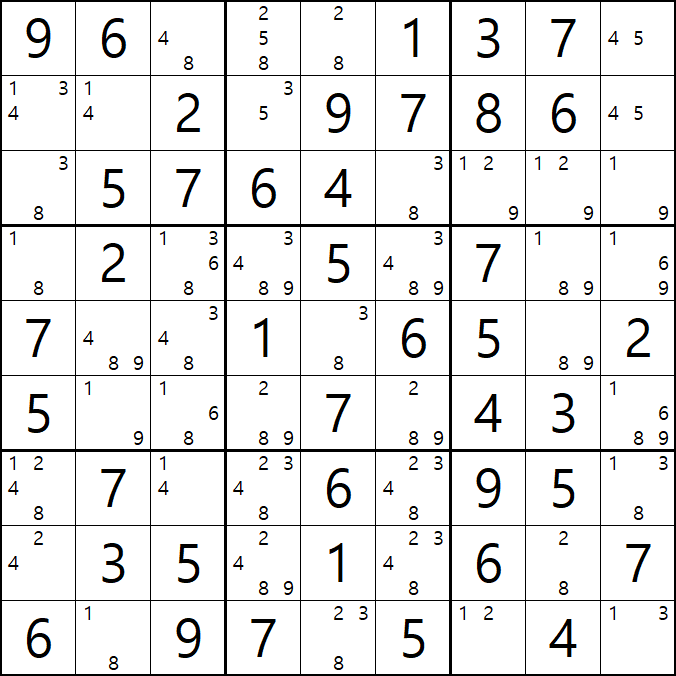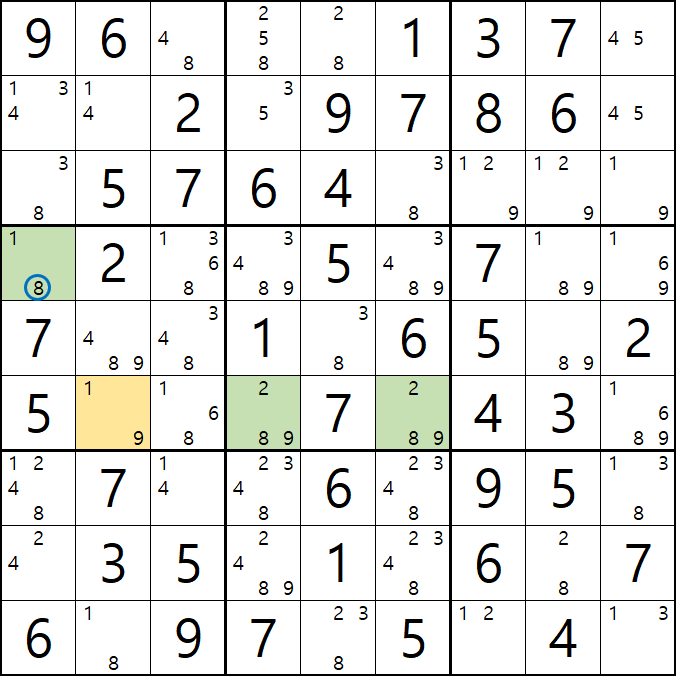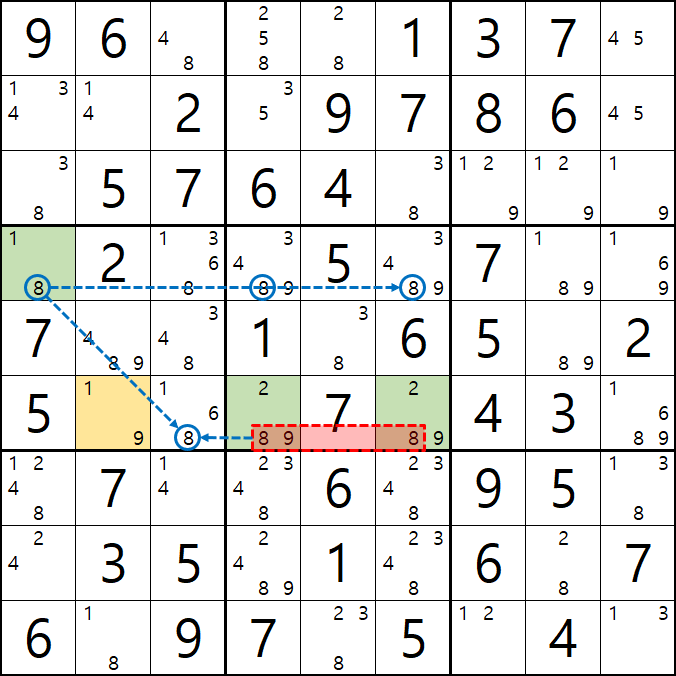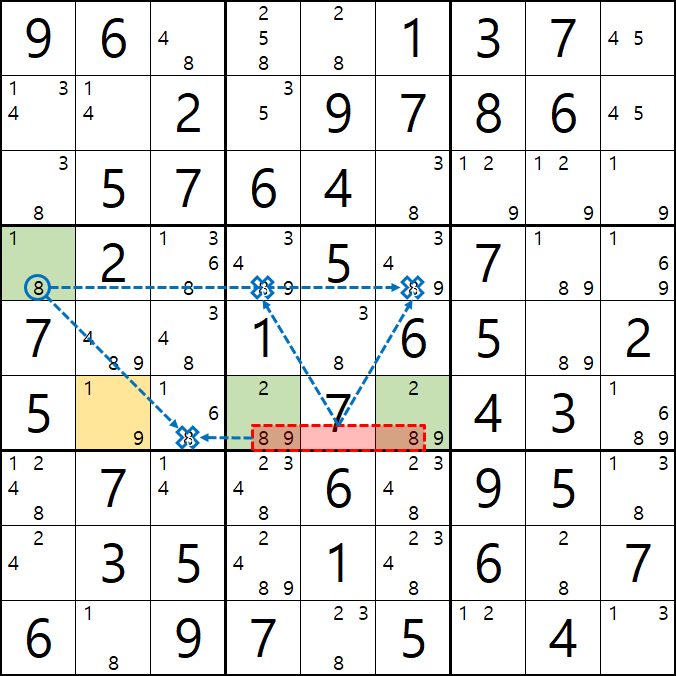
위의 움짤과 같이

 

피벗 1/9[F2]이 되는 칸을 중심으로 1/8[D1], 2/8/9[F4], 2/8/9[F6]인 확실한 쿼드러플이 존재할 경우

박스 4와 박스5를 동시에 볼 수 있는 8[D1]과 8[F4&F6]가 잠근 상태가 되며 동시에 바라보는 

8[F3]과 8[D4], 8[D6]을 제거할 수 있다. 

 

자 일단 내가 할 수 있는 설명은 끝났다. 글에 쓰인 에제 자료는 모두 '스도쿠 위키'라는 사이트에서 가져왔다. 초반에 엄청 어렵다고 한 것 보다는 매우 심플한 공식인 것을 알 수 있다. 확실한 쿼드 보는 연습을 좀 더 하면 더 즐거운 스도커가 될 것이라고 본다. (사실 나도 이 글을 공부의 개념으로 올리는 것이다. 글을 쓰면서 WXYZ윙을 정확히 이해했다~)

 

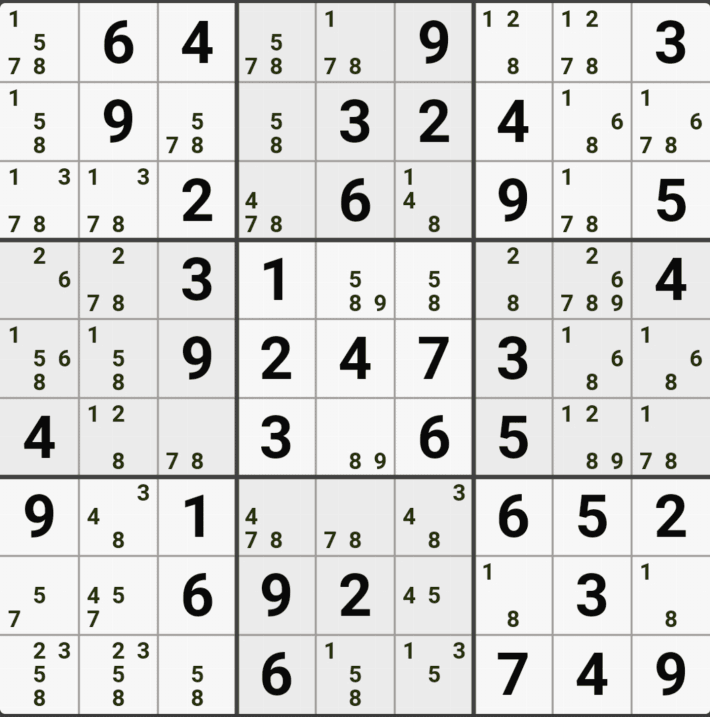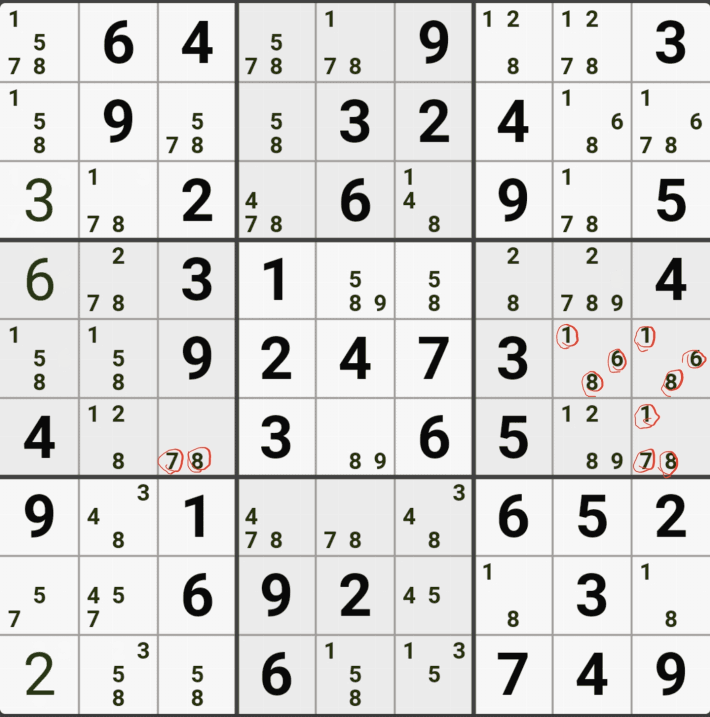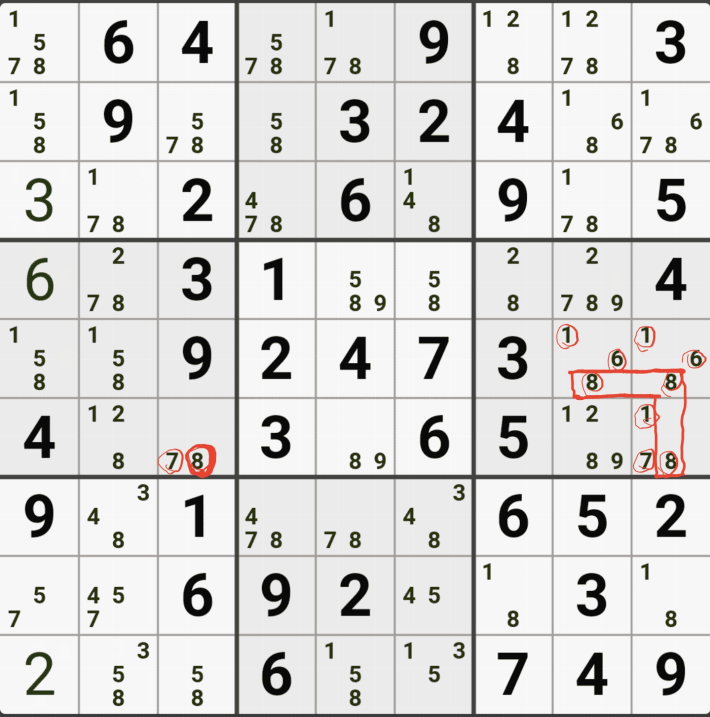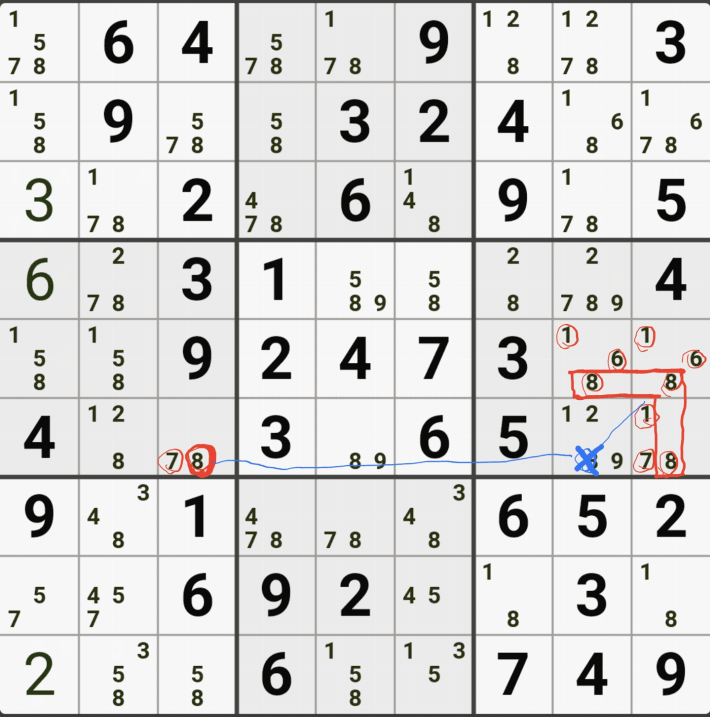
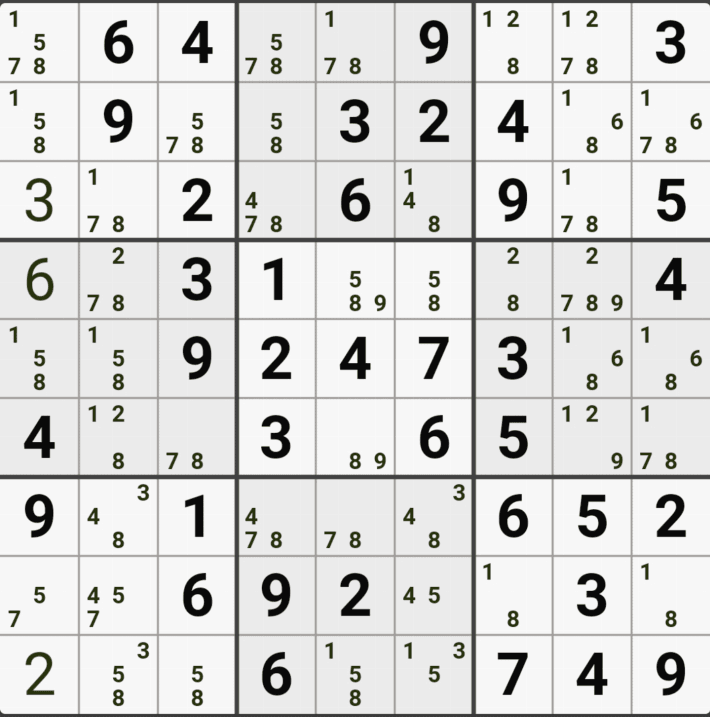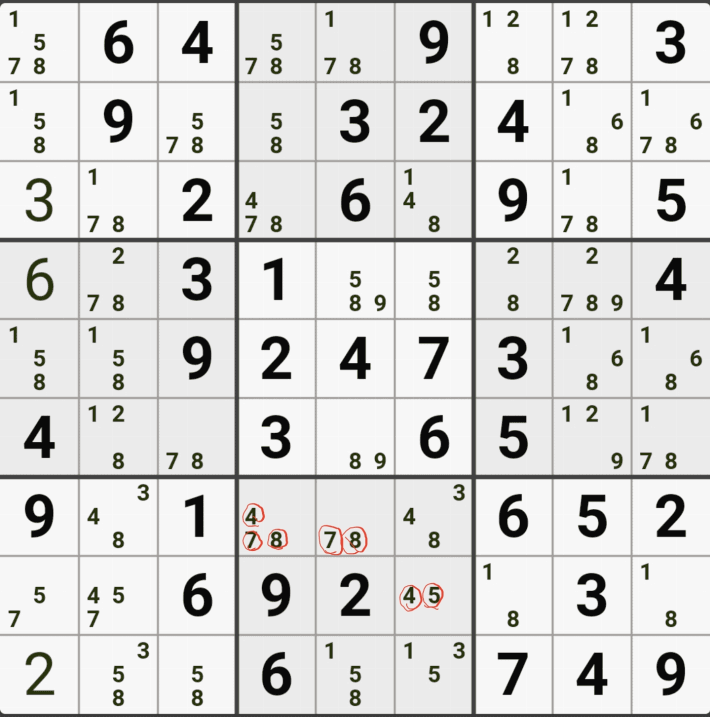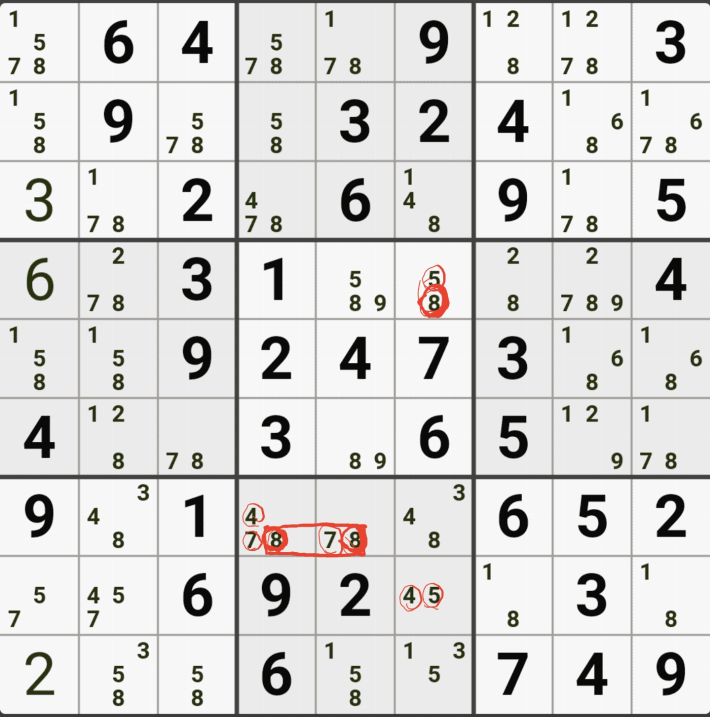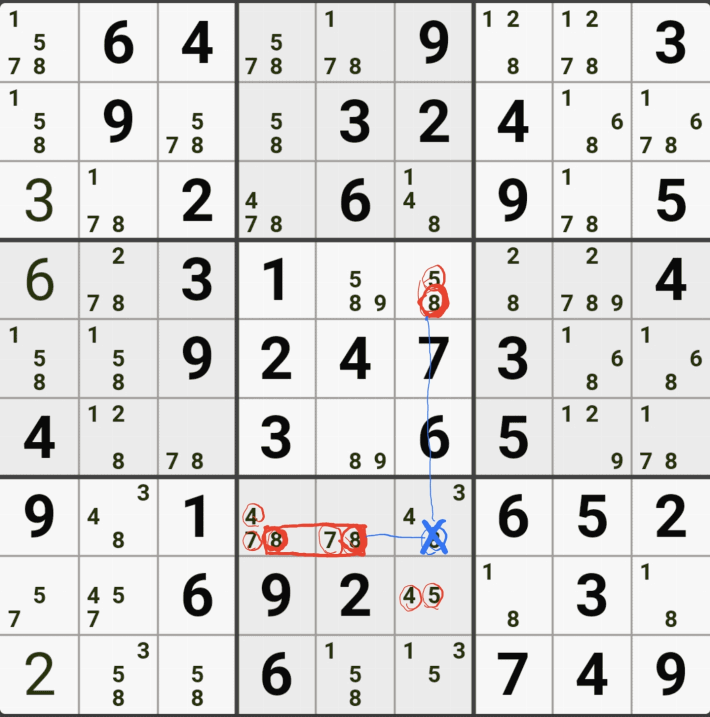
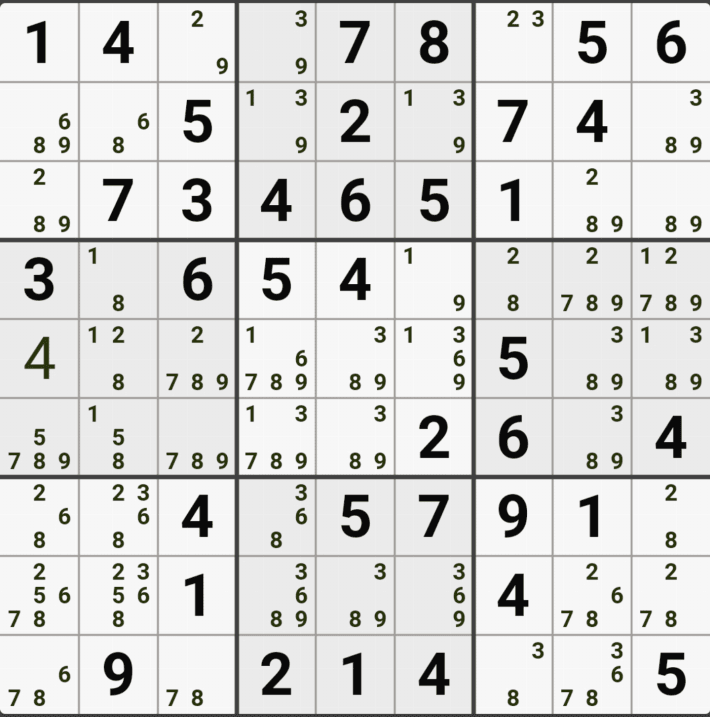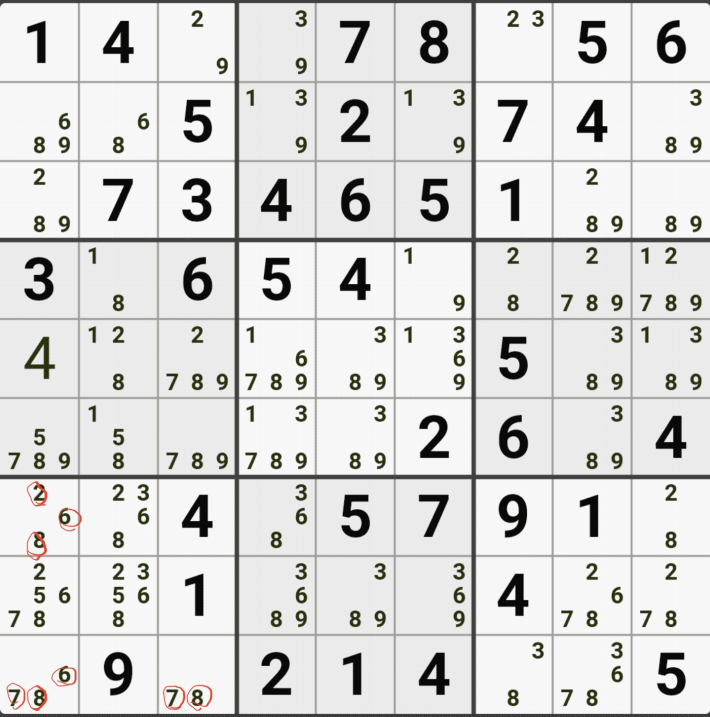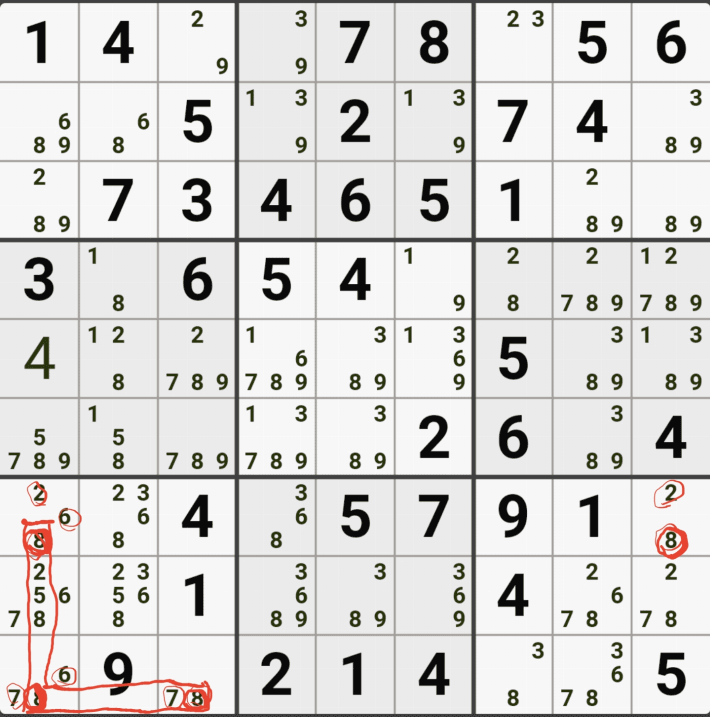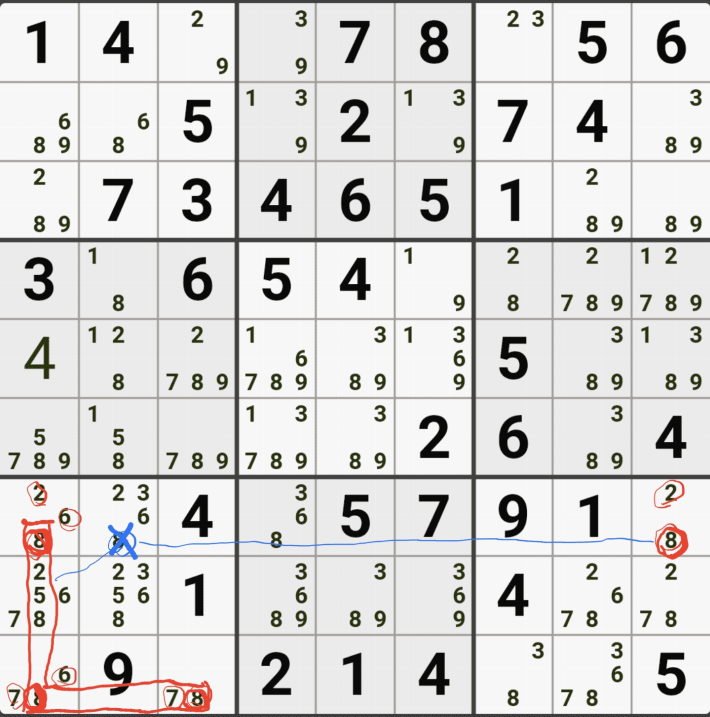
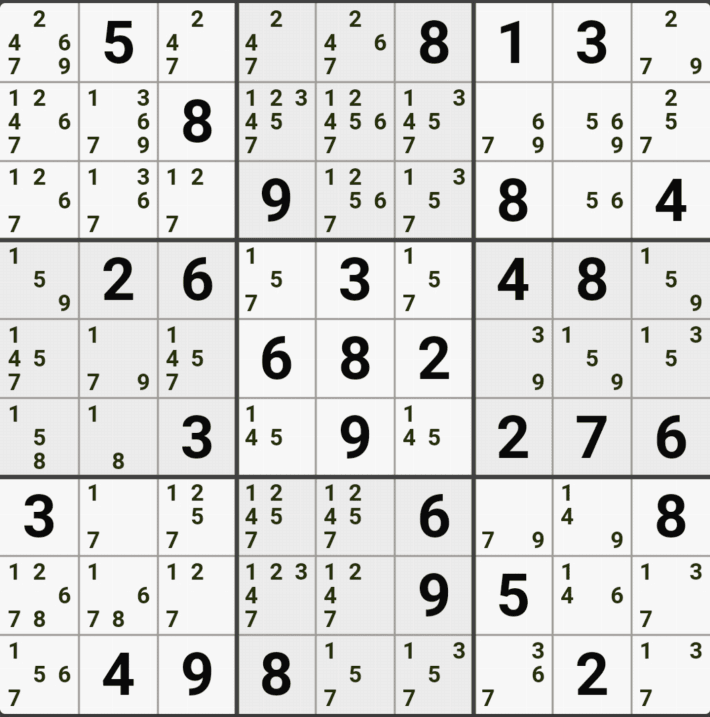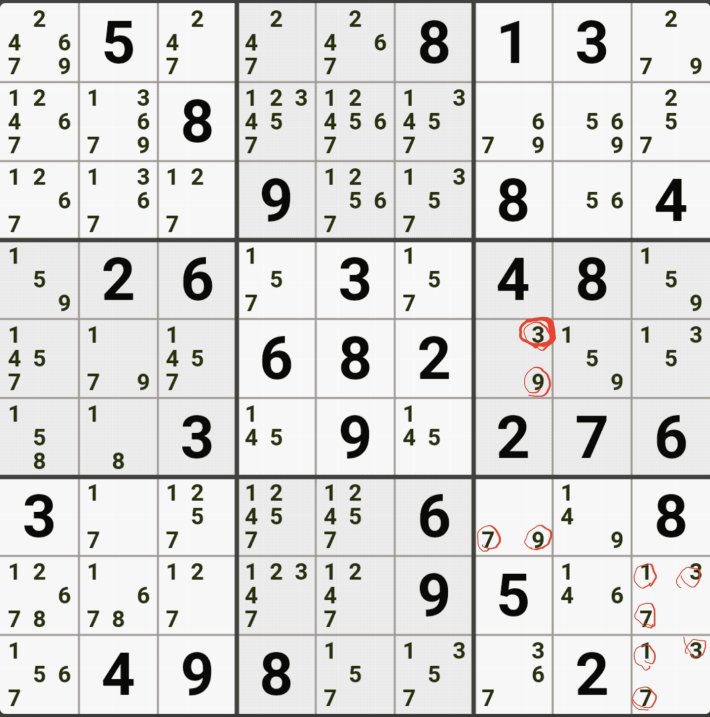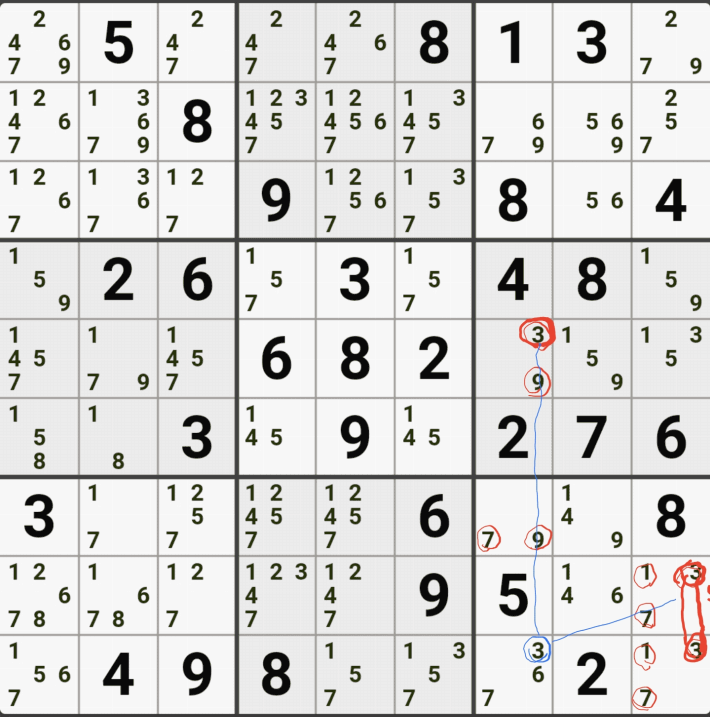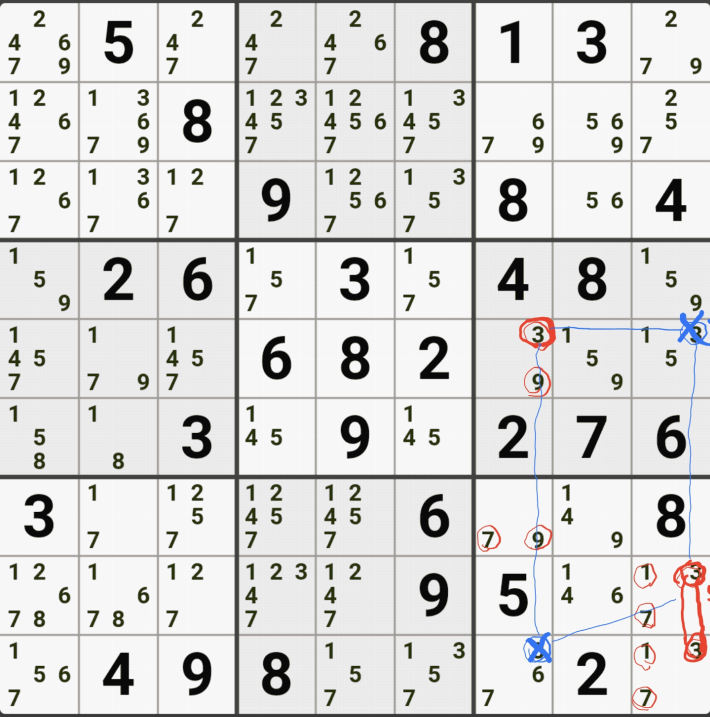
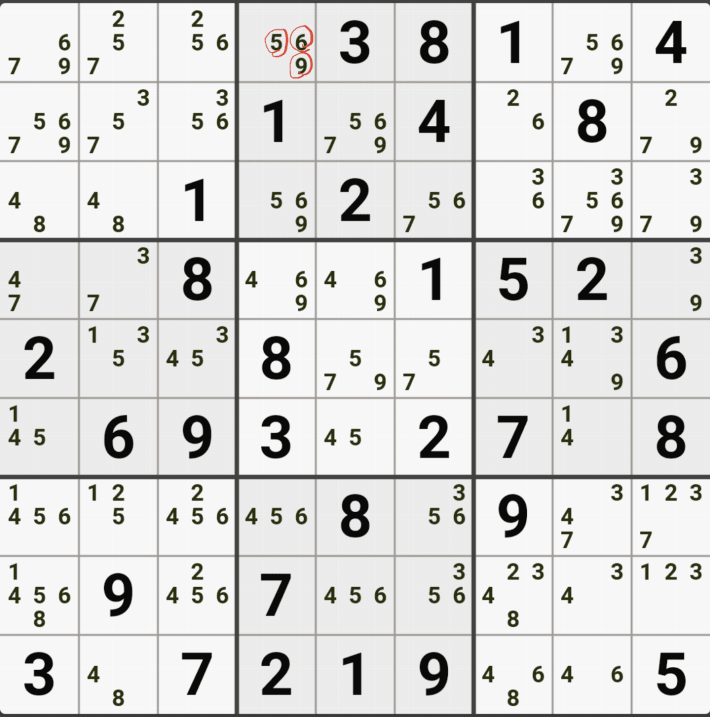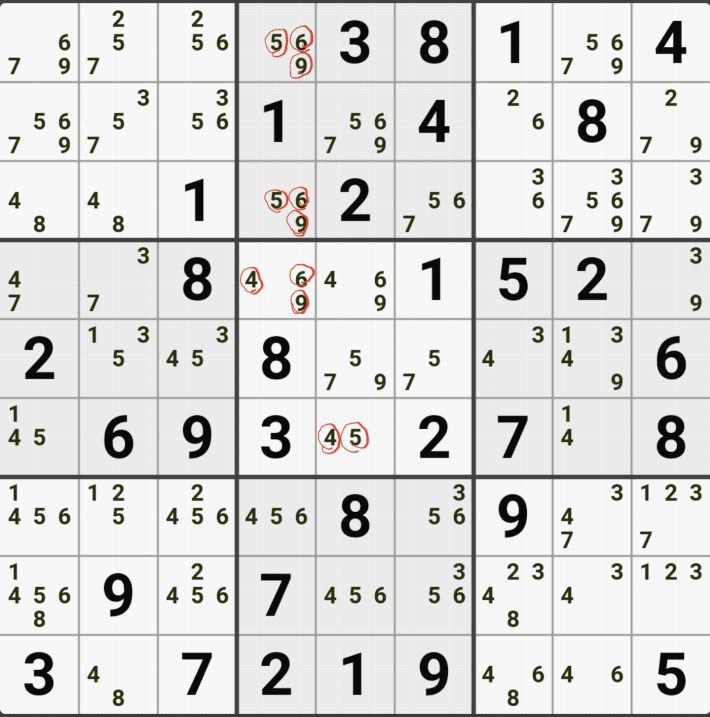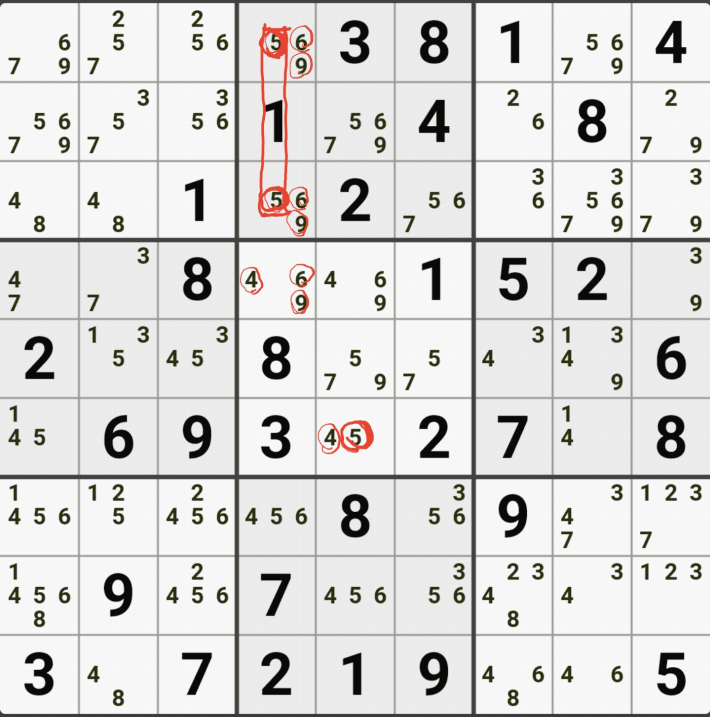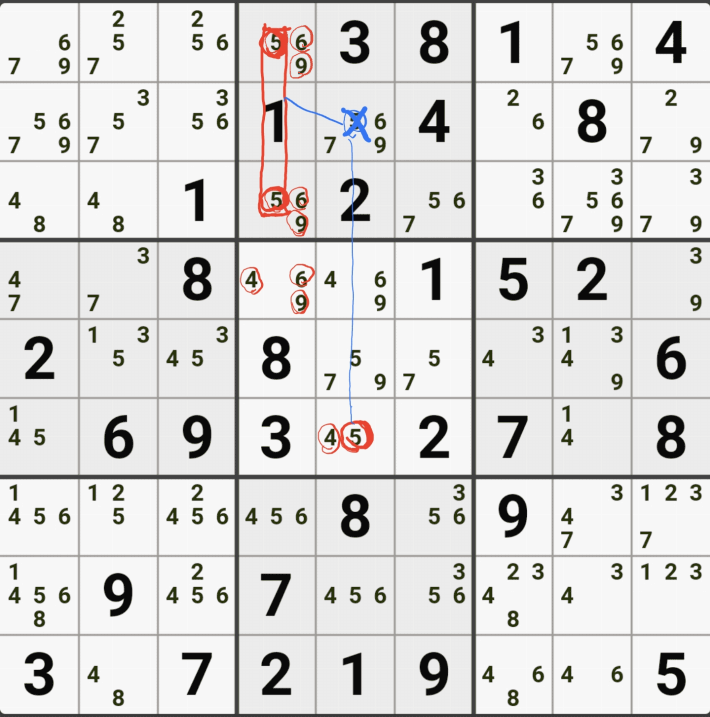
아래는 추가로 움짤 예제를 올린다. 실제 인게임에 수기로 표기한 거라 위에서 본 엑셀로 정리된 움짤에 비하면 (시간이 많이 걸린다.) 좀 지저분해 보일 수 있지만, 다다익선이기 때문에 보자 보자!

 

 따로 설명은 쓰지 않았다.