움짤로 익히는 스도쿠 20. 정렬된 쌍 배제 공식 I(APE)

 이번 글에서는 저 세상 레벨에 속하는 스도쿠 기술인 Aligned Pair Exclusion(APE)에 대해 알아보도록 하겠다. APE는 한국어로 변환하자면 정렬된 쌍 배제'  정도 되겠다. 2가지의 타입이 있는데 이번 글에서는 TYPE 1에 대해서만 알아보도록 하겠다. 한 번에 1,2 모두 보면 머리가 터질 수도 있다. 

 

 APE는 풀하우스가 되기 직전의 후보숫자들의 조합 즉, 이중위치를 갖는다는 성질을 이용하는 스도쿠 공식으로 

형태는 XY윙, XYZ윙, WXYZ윙과 비슷한 패턴을 띄지만 접근방식은 전혀 다르다.

 

 패턴 자체는 BUG에 좀 가까워 보인다. 

 

움짤예제 0. BUG 패턴 - APE와 마찬가지로 마지막 남은 3개 남은 후보숫자를 이중값을 갖는 숫자에서 추론하는데, 방식이 다르긴 하다. 

 

하지만 APE 또한 BUG와 마찬가지로 우리가 아는 각 공식을 써서 궁극적으로는 풀하우스 직전의 XY, YZ, ZX 등으로 인수분해 되는 성질을 이용하는 것인데...

 

음. 스도쿠를 글로 풀려니 나도 힘이 든다. 움짤은 보면서 APE를 정의하고 설명하도록 하겠다. 

 

 

 

움짤 예제 1. XY윙 적용 (박스1~3)

 

위의 움짤은 워밍업으로 XY윙 공식을 적용하여 

-8[A9] +2[A9] -2[A2] +4[A2] -4[B1] +8[B1] -8[A3] -8[B7] 이 되어 

A행에 -8[A9] -8[A3], 박스3에 -8[A9] -8[B7] 이 동시에 존재하는 모순이 발생하므로

모순을 제거 하기 위해 -8[A3] -8[B7]은 제거되어야 한다.

 

위의 움짤예제1. 을 이제 박스4~6에 APE 공식을 적용해 풀어 보겠다.

 

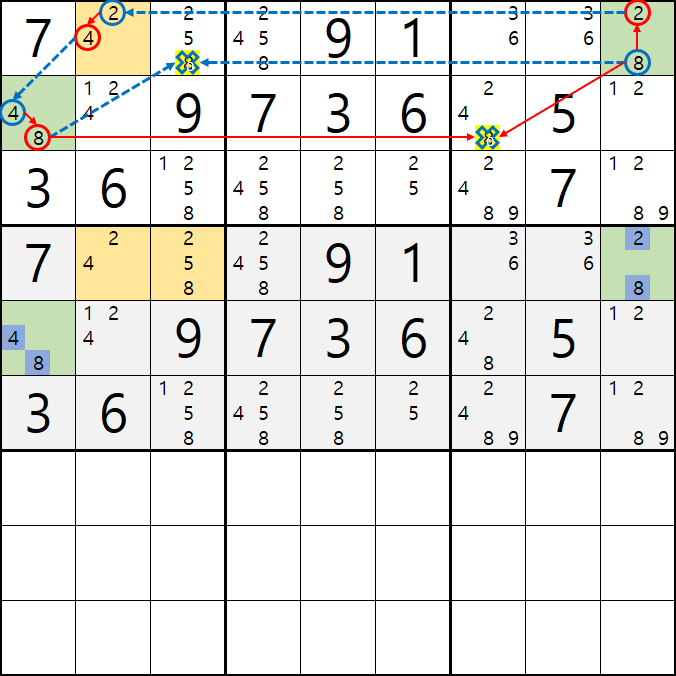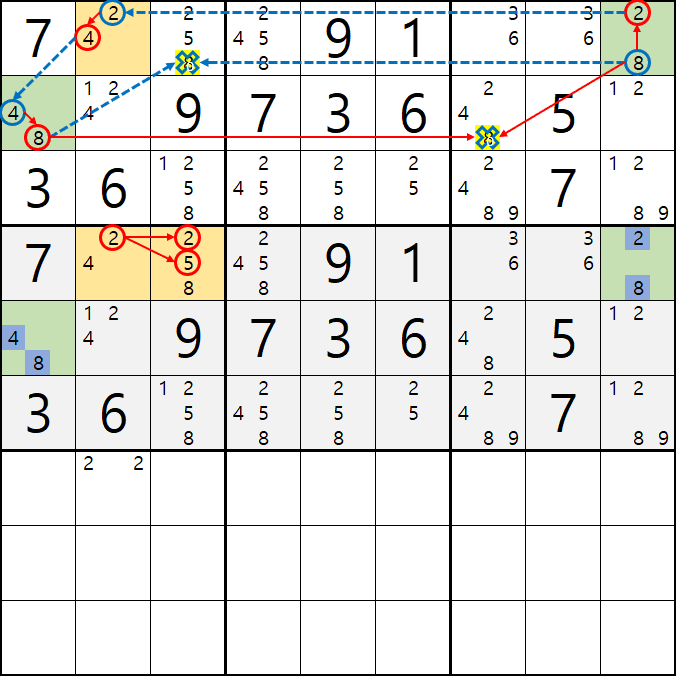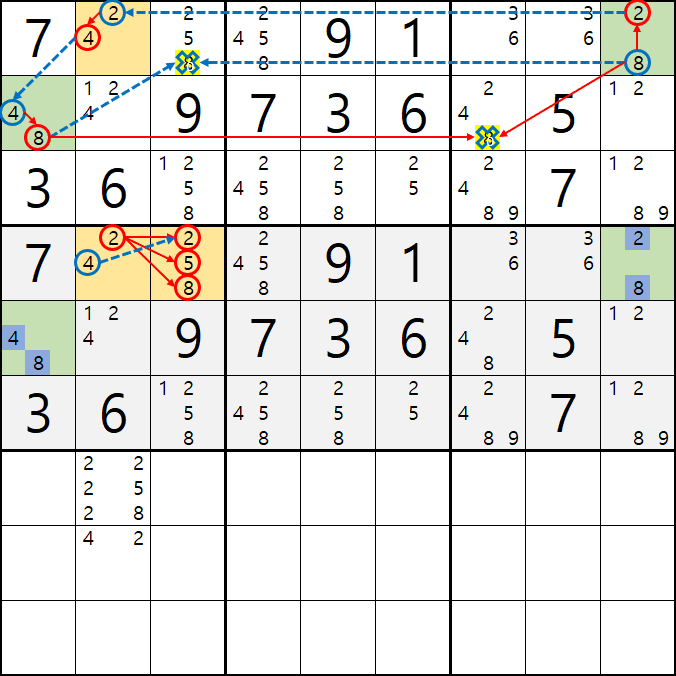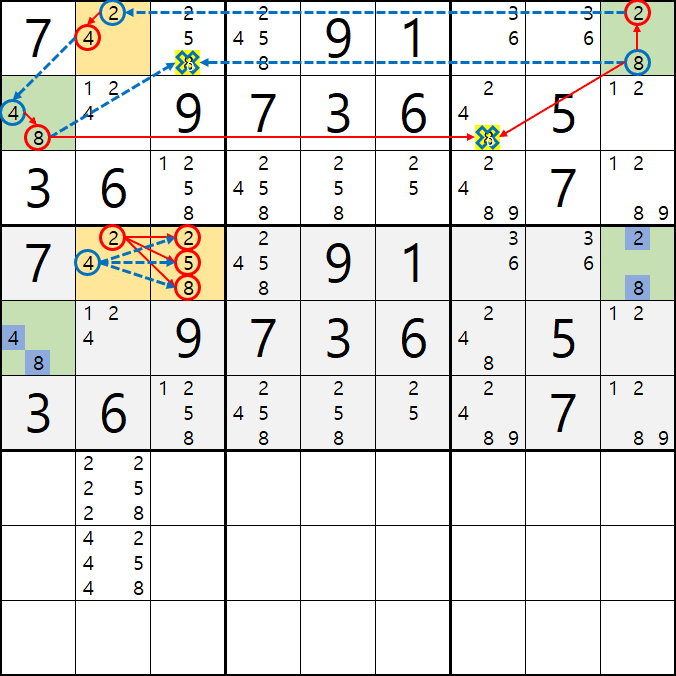
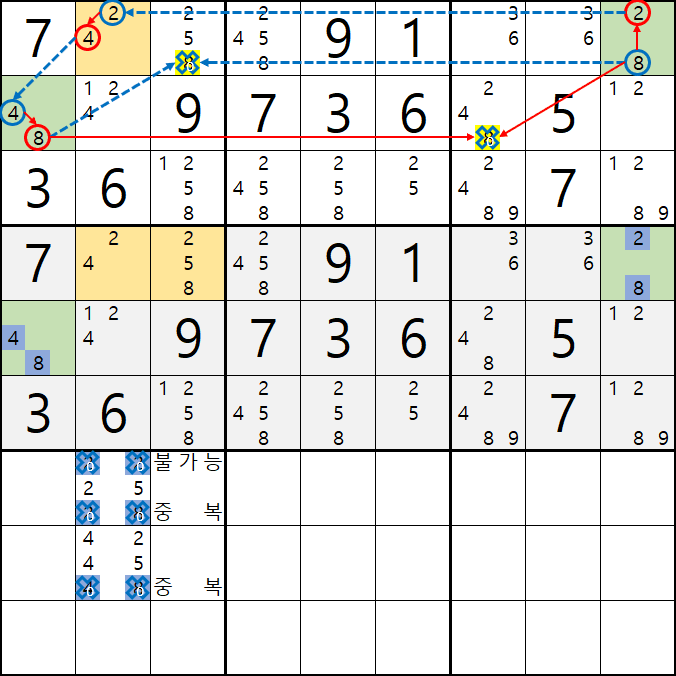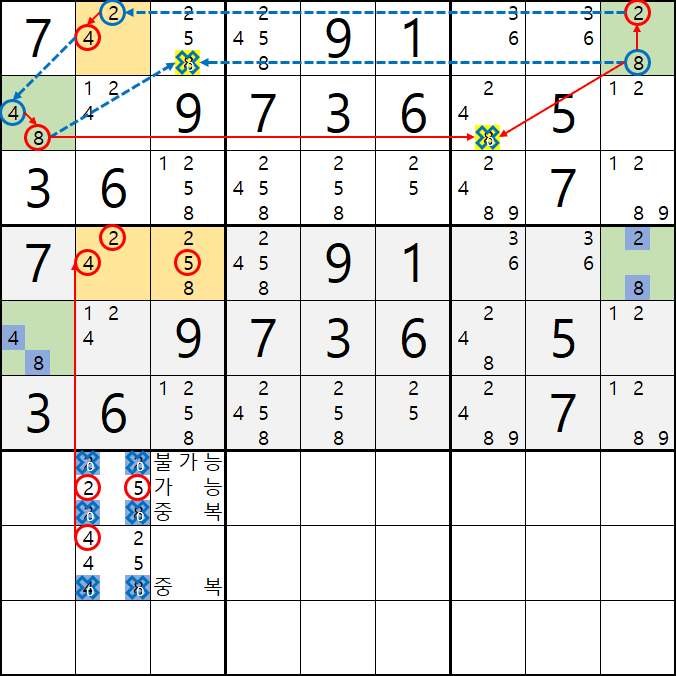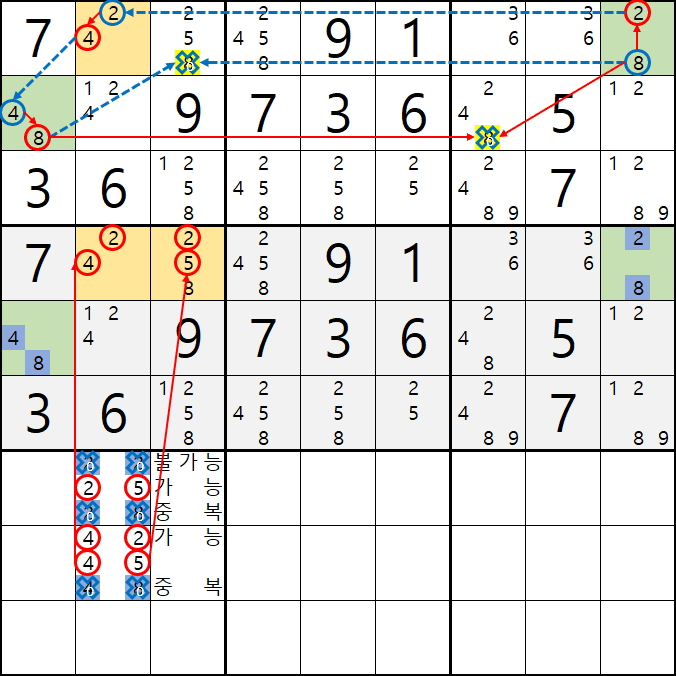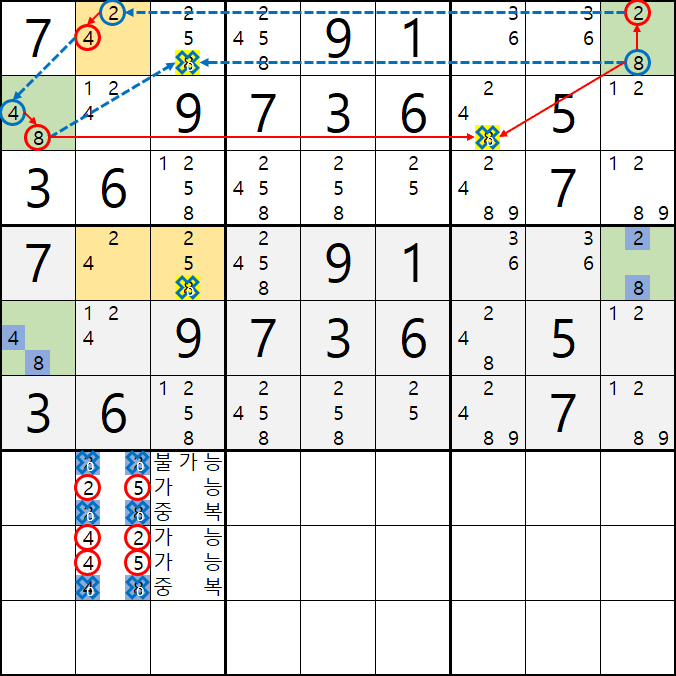
움짤 예제 2. 움짤 예제 1. 과 동일한 상황에서 APE(피벗 2칸, 핀 1+1칸) 적용 (박스4~5)

 

2-1. APE 공식 베이스 찾기.

 

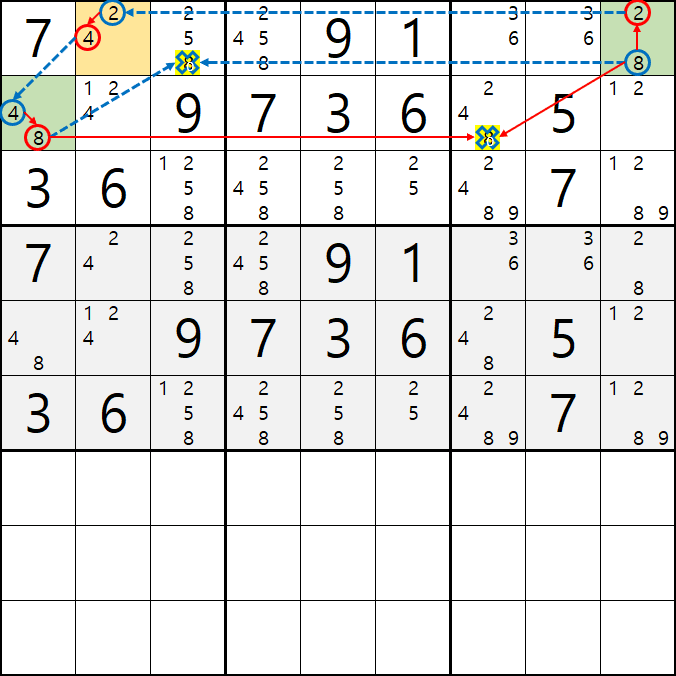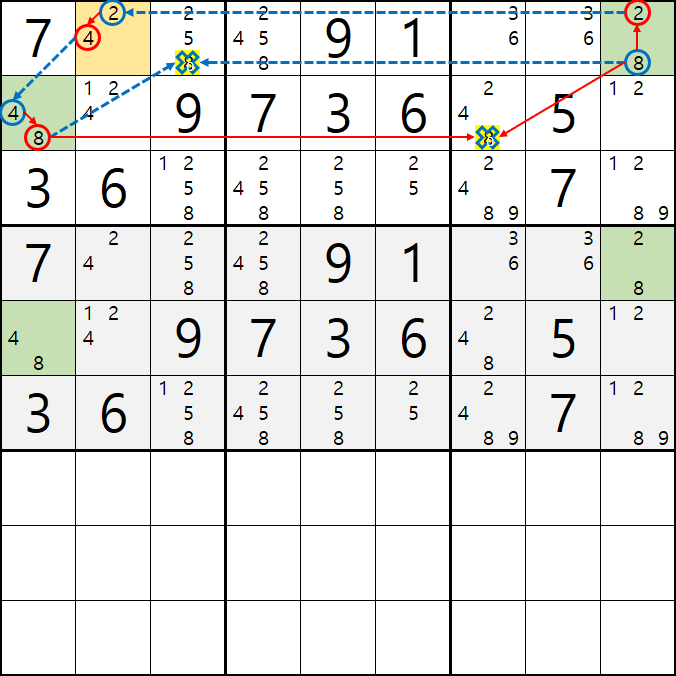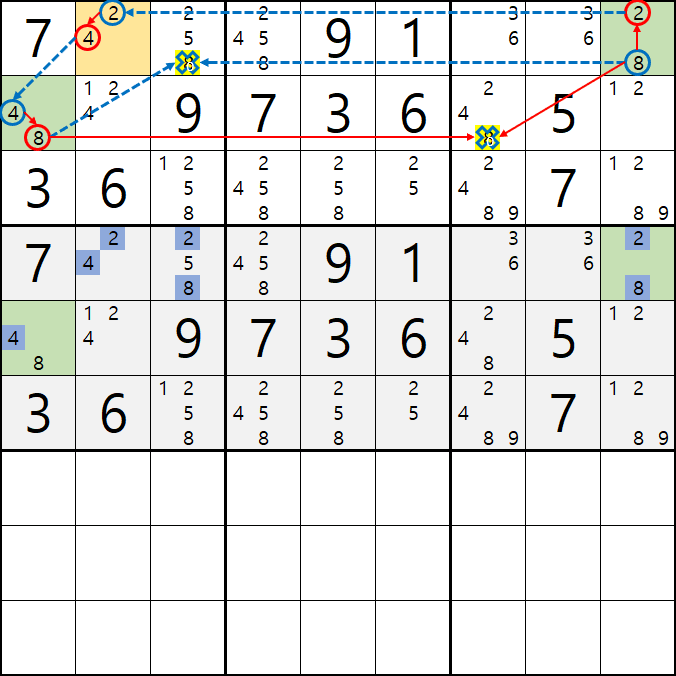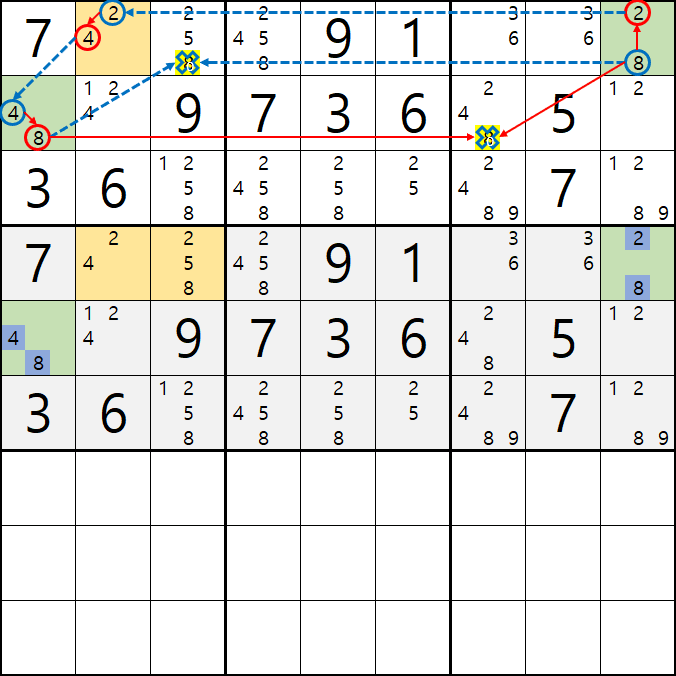
핀이 되는 4/8[E1]과 2/8[D9]이

동시에 마주보는

2/4[D2]와 2/5/8[D3] 이

피벗이면서 APE 공식을 적용할 타겟이 된다.

 

2-2. 우리가 알던 개념에서 좀 더 확장된 개념인데,

타겟이 되는 2개의 칸인

2/4[D2]와 2/5/8[D3] 에서 조합되는 모든 경우의 수를 아래와 같이 나열하면

22 / 25 / 28

42 / 45 / 48

(24라고 적지 않는다 칸대칸으로 순차적으로 적는다.)

이라는 모든 경우의 수로 조합이 되는데...

 

2-3. 위의 조합된 수를 핀이 되는 칸과 비교를 해보면 아래 움짤과 같이

 

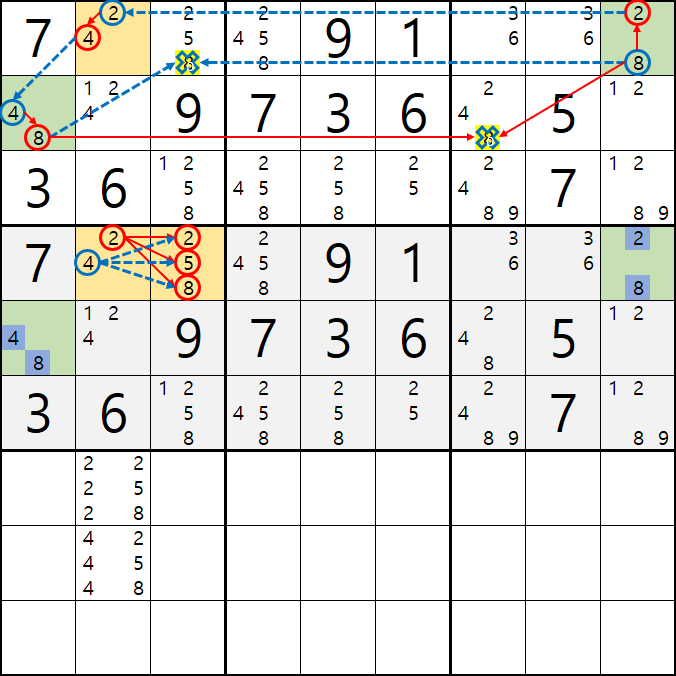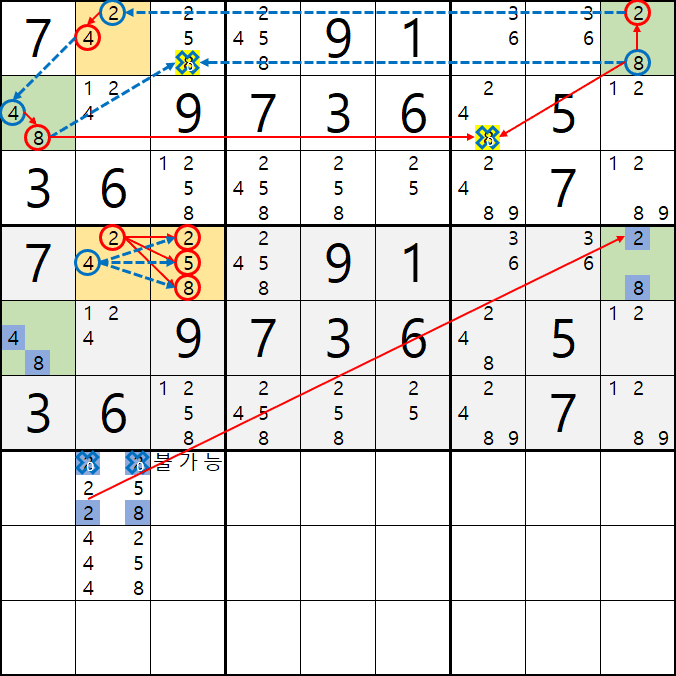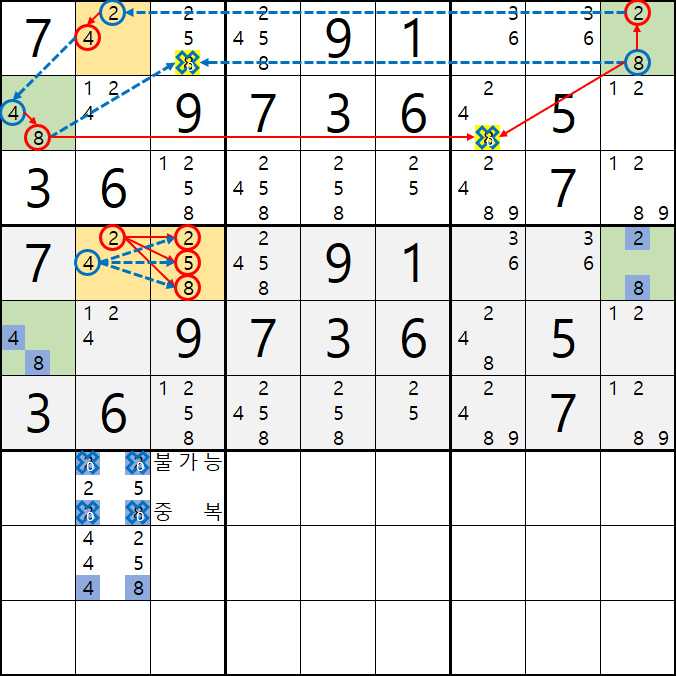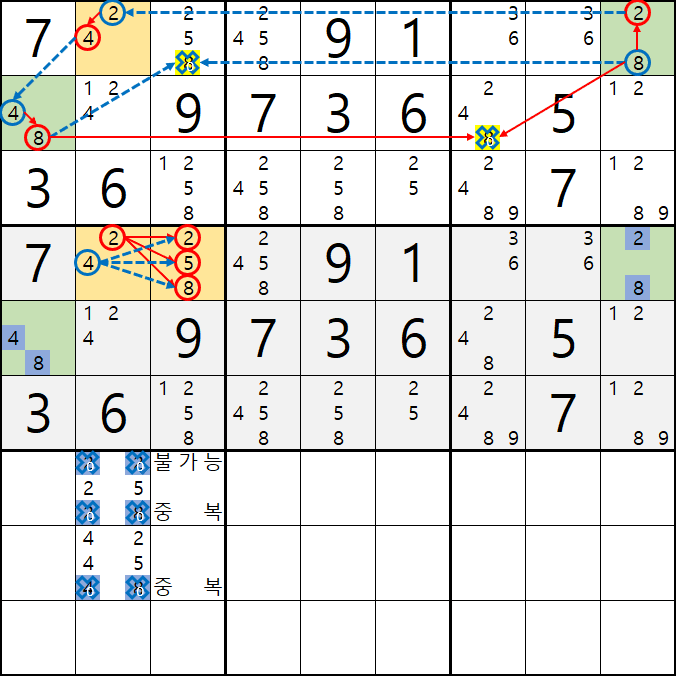
22는 스도쿠 제 1 규칙에 위배 되기 때문에 불가능하고

28은 2/8[D9]와 중복이 되어 불가능한 조합이 되고

48은 4/8[E1]과 중복이 되어 불가능한 조합이 된다. 

 

2-4. 따라서 

2/4[D2]와 2/5/8[D3] 에 조합이 가능한 숫자는 아래 움짤과 같이

25 / 42 / 45 가 되는데...

 

 

위의 분석된 숫자 조합을 짤로 줌해서 보면 

 

D2, D3의 숫자조합에서 후보숫자 8이 제외되고 2 또는 5만 들어가는 조합만 가능하다는 것을 알 수 있다. 

이를 다시 숫자 조합만 보면

22

25

28

42

45

48

가 되어 D3 포지션의 후보숫자 8이 배제 되는 것을 알 수 있다.

즉, APE공식에서 8[D3] 을 제거할 수 있는 것이다. 

 

사실 APE공식은 찾는 것이 어렵다. 찾으면 아래와 같이 약식으로 

핀이 되는 칸의 숫자를 먼저 파악하고 조합해 보면 답을 암산으로 계산이 가능할 수도 있다. 

 

핀이 되는 4/8[E1]과 2/8[D9]의 숫자를 조합하면

4/8[E1],  2/8[D9]은 출현되어 있고 잠재적인 조합은 4/2 및 8/8인데 불가능한 조합이라

실질적으로 존재하는 4/8, 2/8 잠재적으로 존재하는 4/2의 조합을 먼저 보면 되겠다. 

 

그래서 피벗이 되는 2/4[D2]와 2/5/8[D3]에서 

2/8 중복, 4/8 중복, 4/2 가능하므로

8을 포함한 조합은 제외 되는 것을 알 수 있다.

즉, 8[D3]을 제거할 수 있다.

 

  

 

움짤 예제 3. 동일한 상황에서 APE (피벗 2칸, 핀 1+3칸)

 

3-1. 아래 움짤과 같이

 

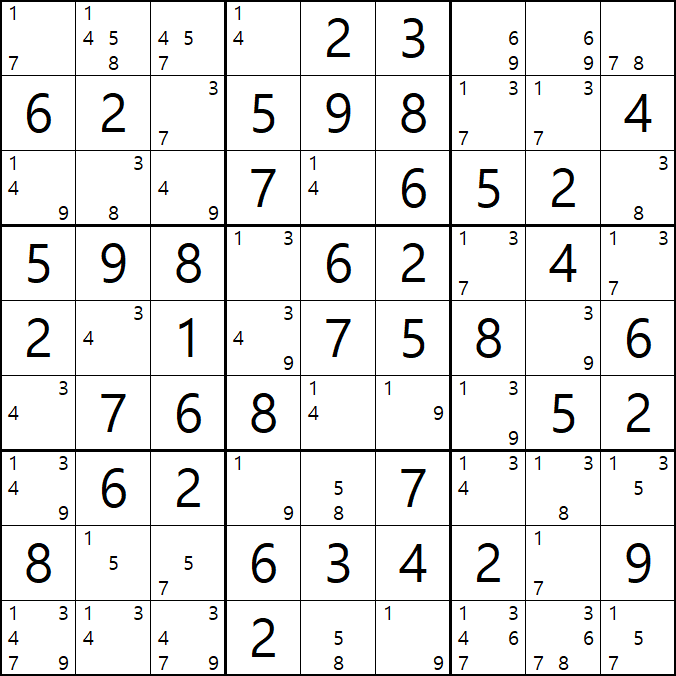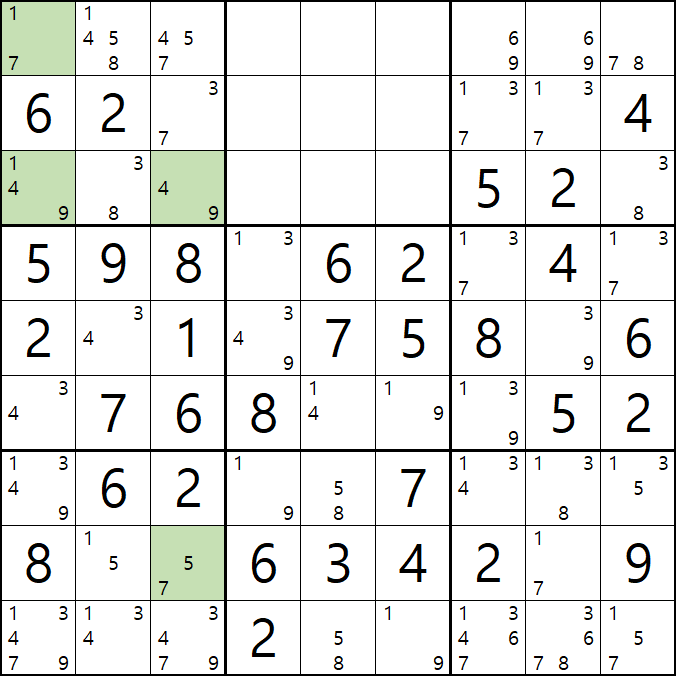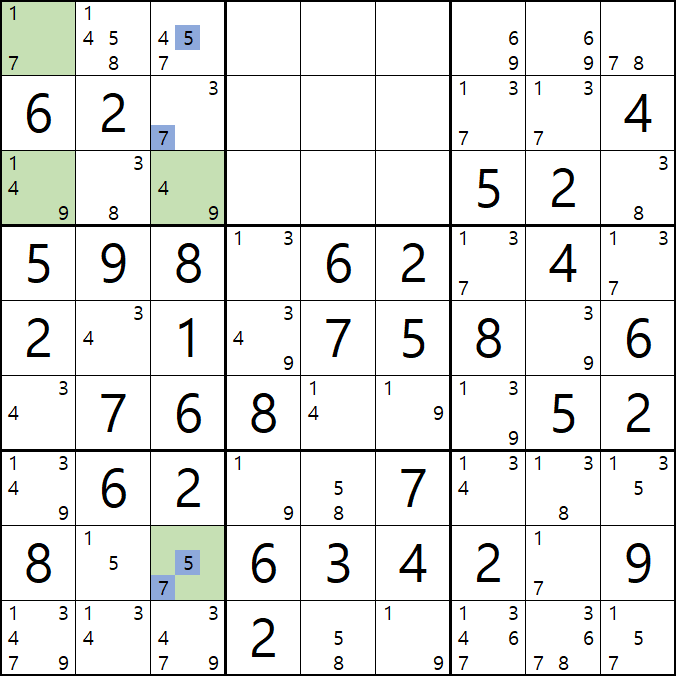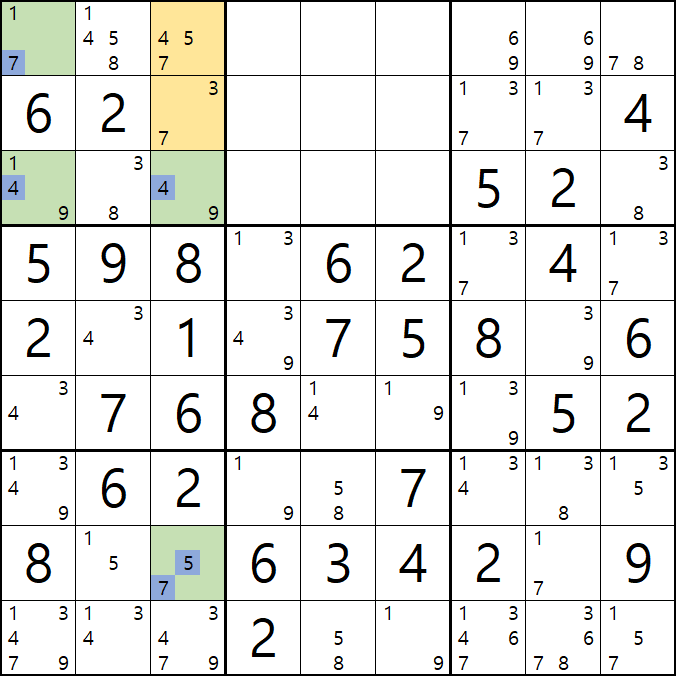
핀이 되는 3열의 5/7[H3]과 박스3의 1/7[A1], 1/4/9[C1], 4/9[C3] 이 동시에 마주보는 

4/5/7[A3]과 3/7[B3]이 피벗이자 타겟칸이 되어 

 

3-2. 아래 움짤과 같이 

 

43 - 47 - 53 - 57 - 73 - 77의 숫자 조합이 가능하게 되는데

 

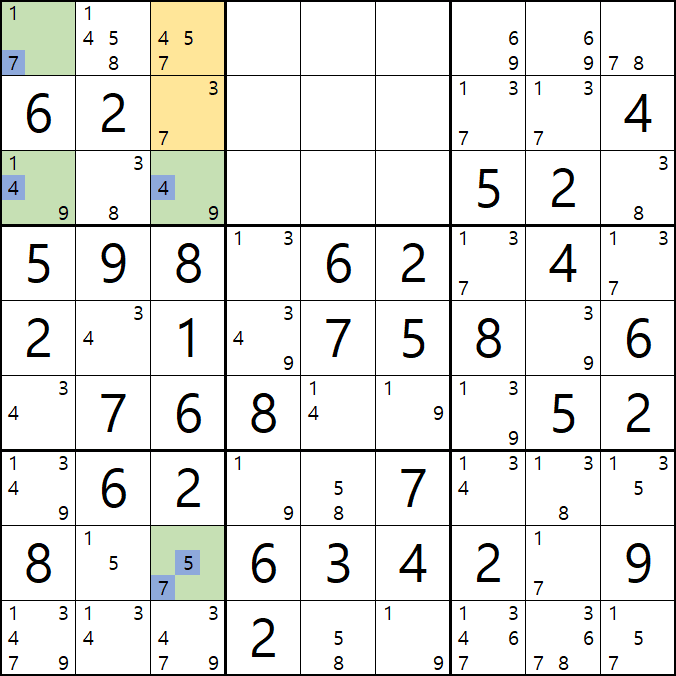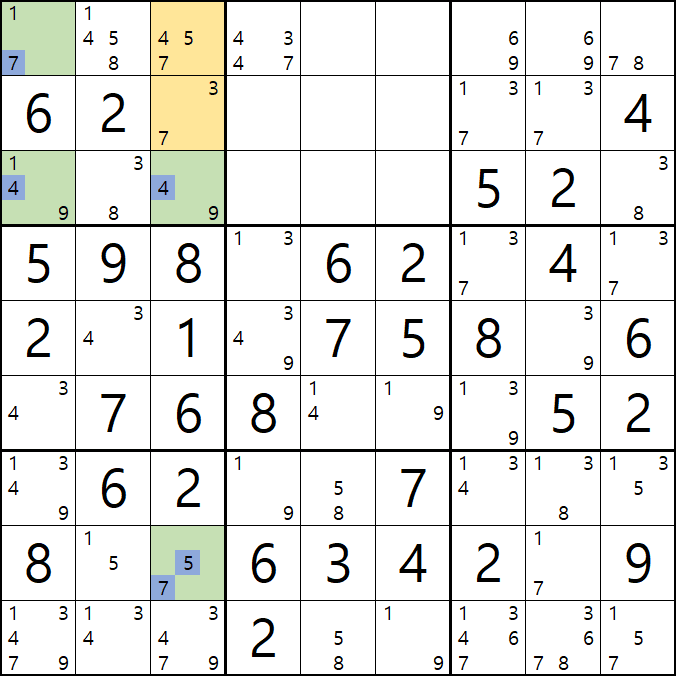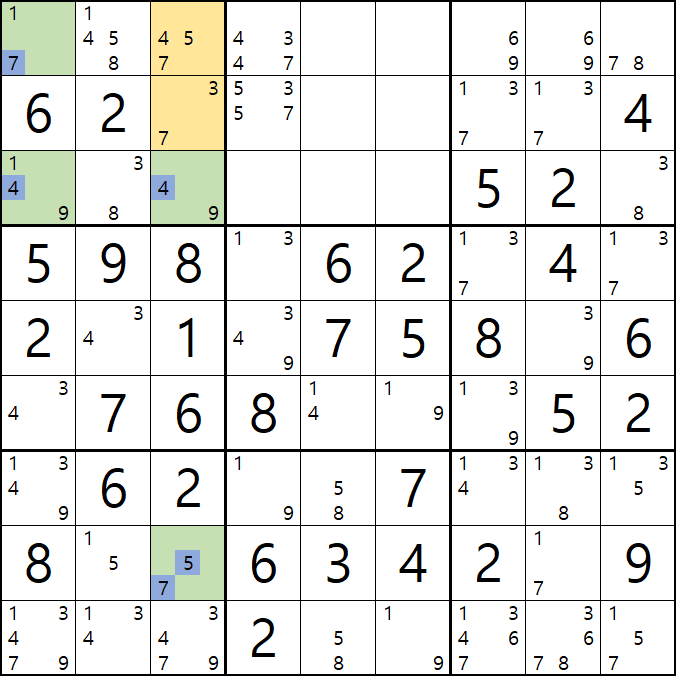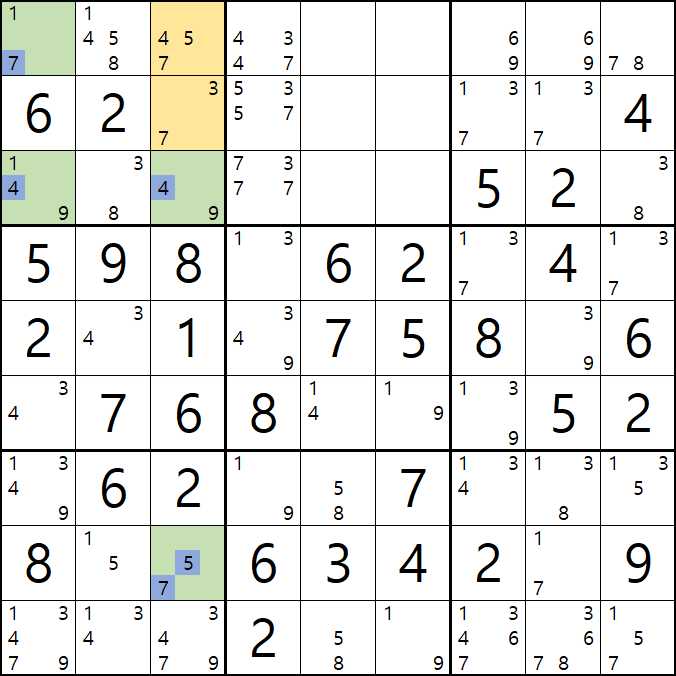
3-3. 조합된 숫자 중에서 

 

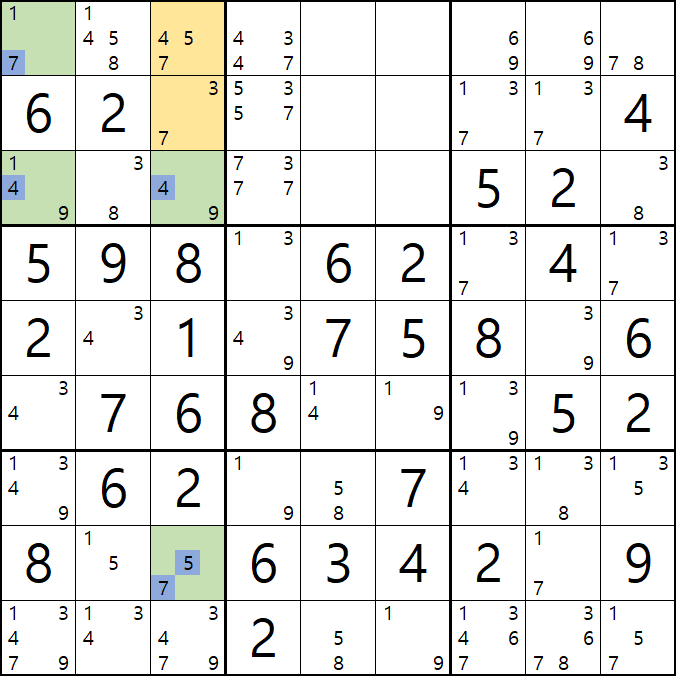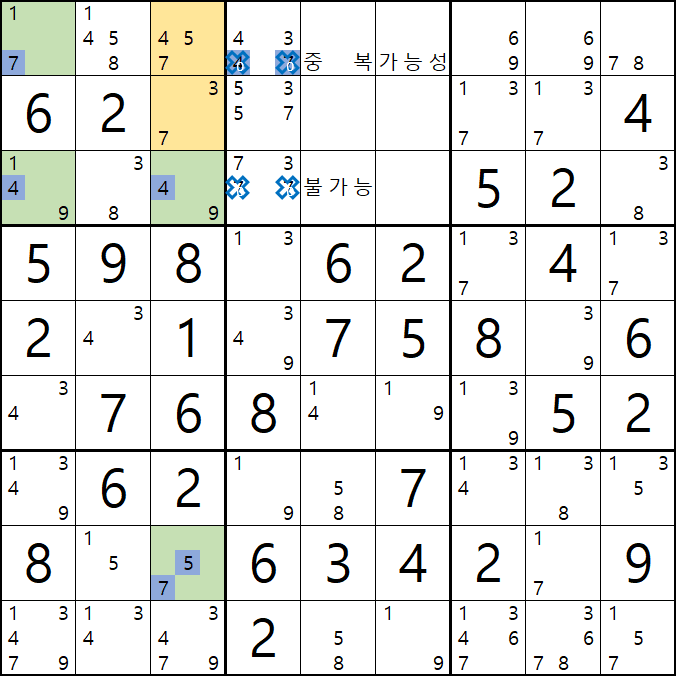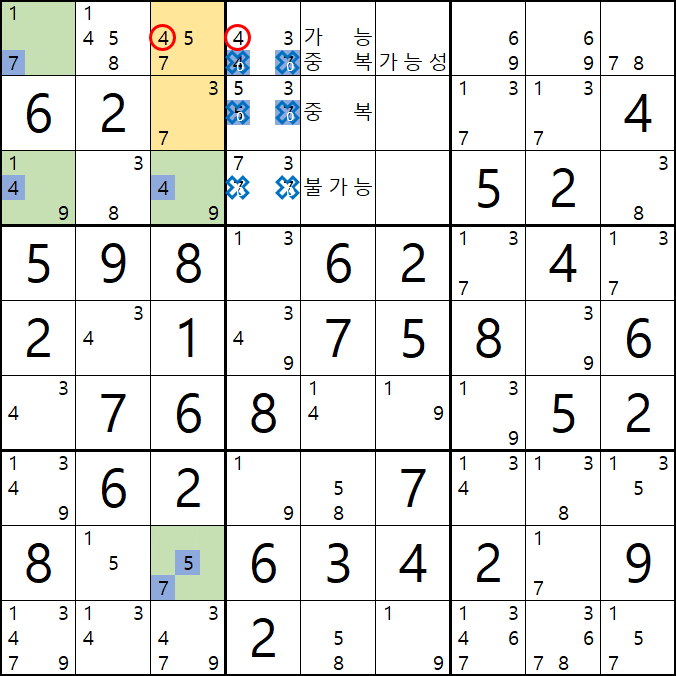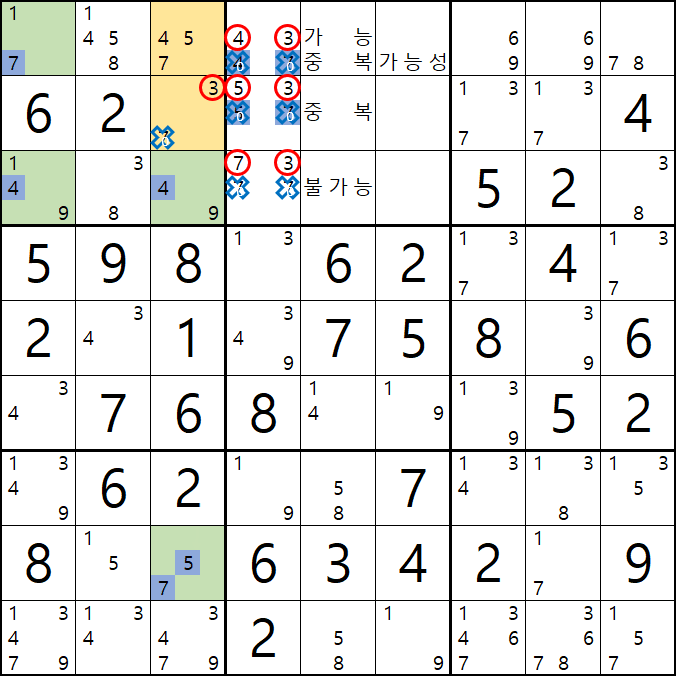
77은 스도쿠 규칙에 위배되는 조합이고

47은 1/7[A1], 1/4/9[C1], 4/9[C3]의 조합에서 중복이 될 가능성이 잠재되어 있어서 불가능한 조합이 되고

75는 5/7[H3]과 중복이 되기 때문에 불가능한 조합이 된다. 

 

피벗 칸에서 조합이 가능한 숫자를 살펴 보면 

43 / 53 / 73으로 B3칸 포지션에는 7이 배제 되는 것을 알 수 있다. 

즉, 7[B3]을 제거할 수 있다. 

 

 

움짤 예제 4. APE(피벗 2칸, 핀 2+2칸)

 

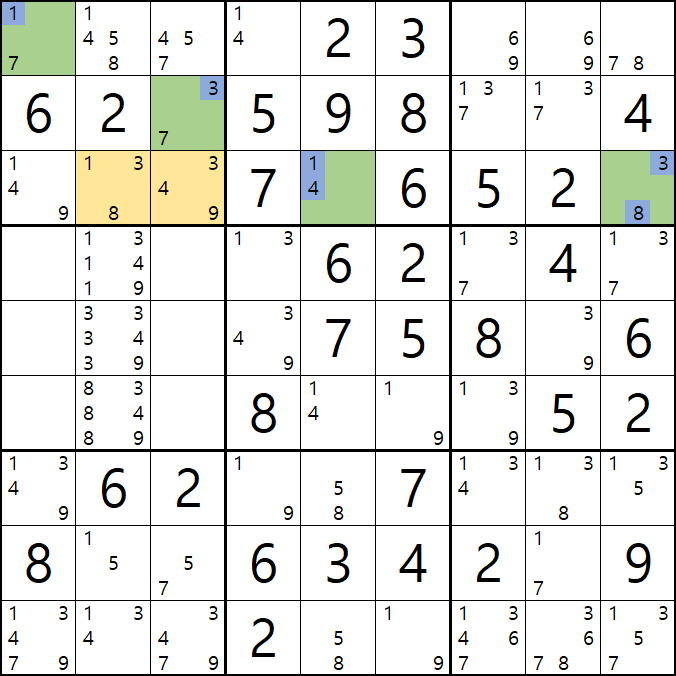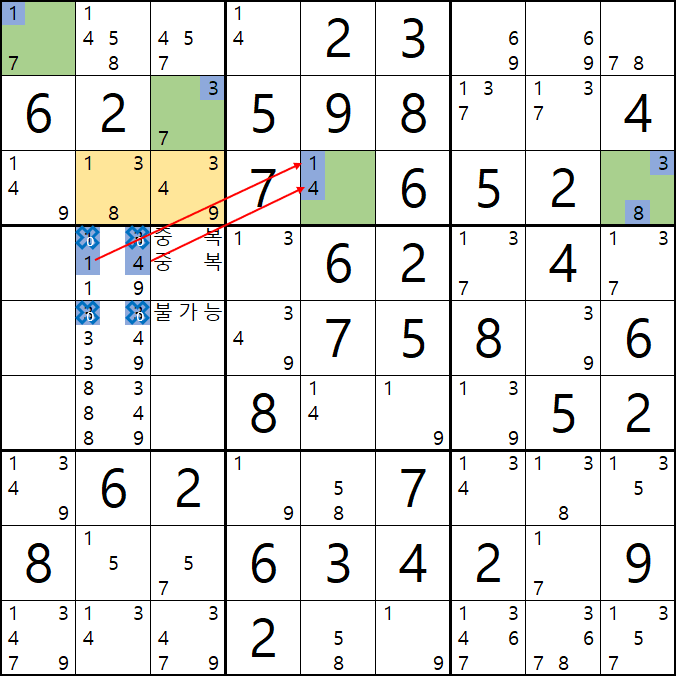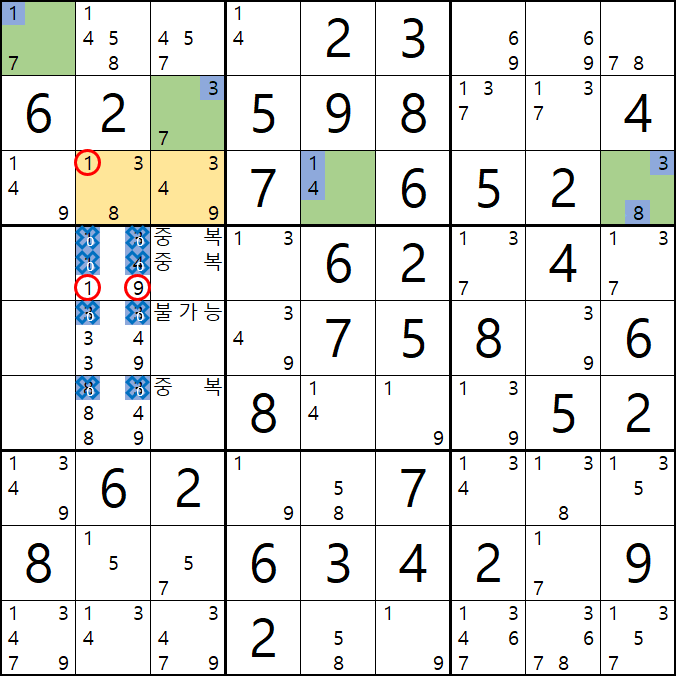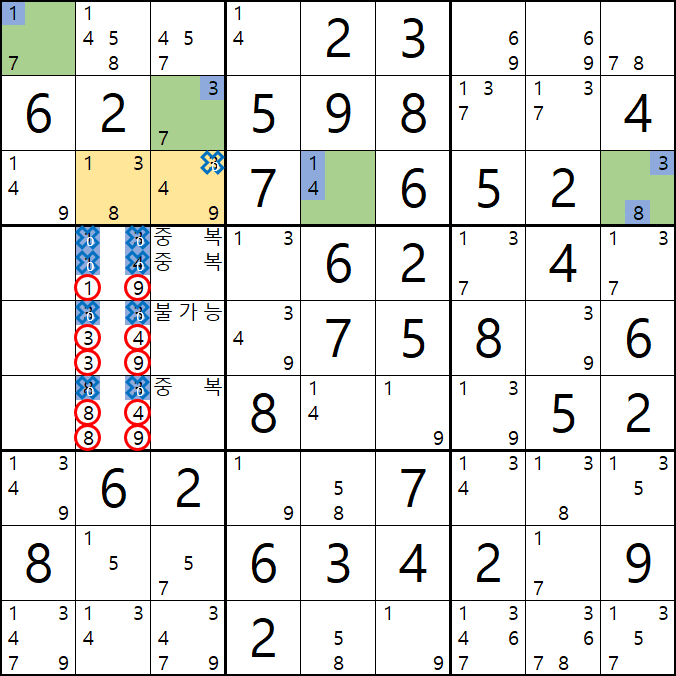
4-1. 아래 움짤과 같이

 

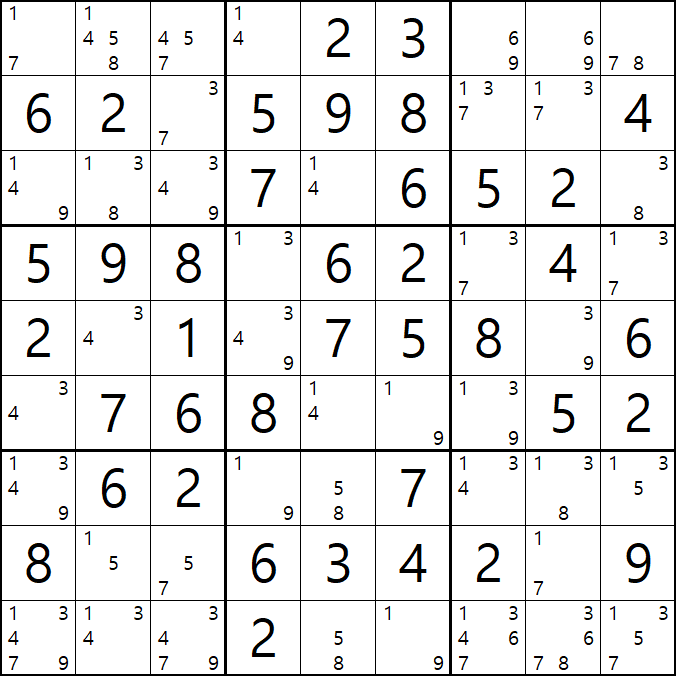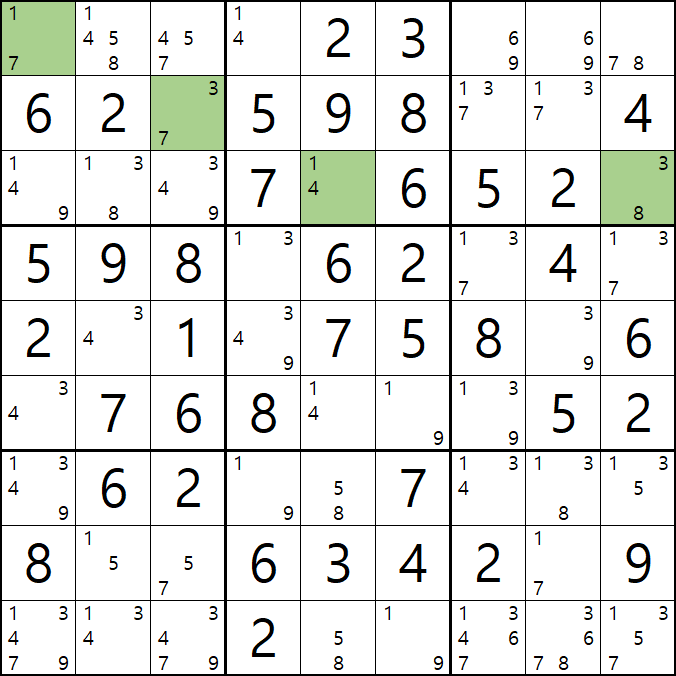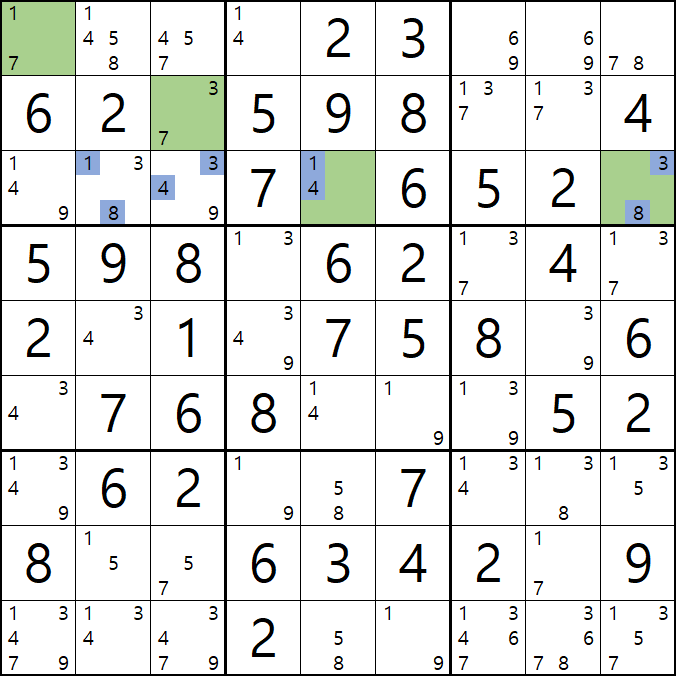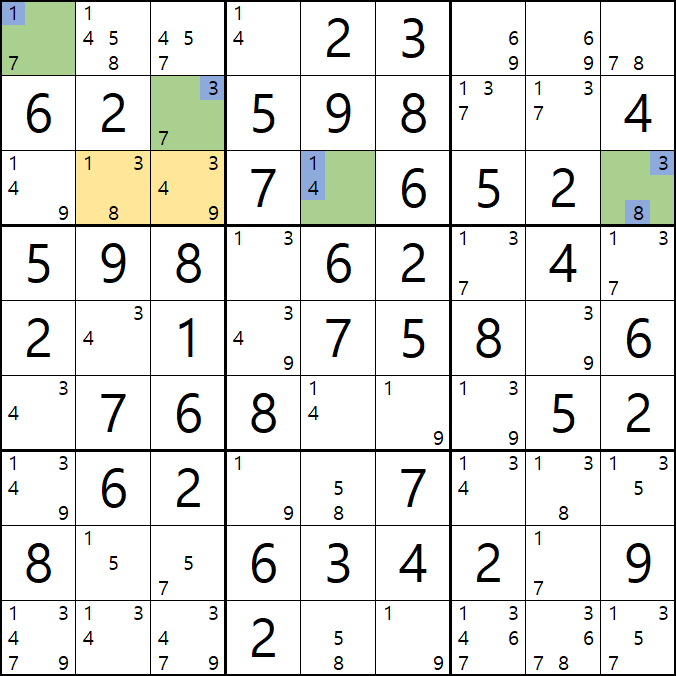
핀이 되는 C행의 1/4[C5]와 박스3의 3/8[C9]와 박스1의 1/7[A1], 3/7[B3] 이 동시에 마주보는 

1/3/8[C2]와 3/4/7[B3]이 피벗이자 타겟칸이 되어 

 

4-2. 아래 움짤과 같이 

 

13 - 14 - 19 - 33 - 34 - 39 - 83 - 89의 숫자 조합이 가능하게 되는데

 

 

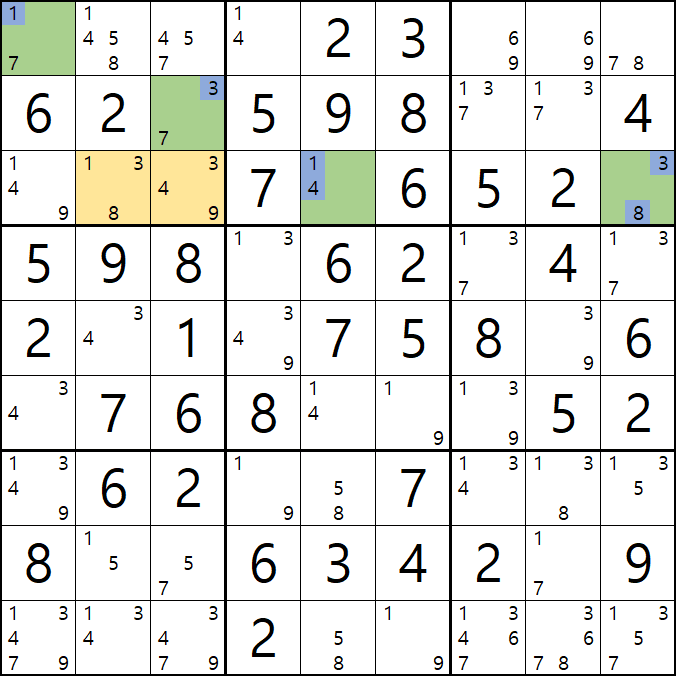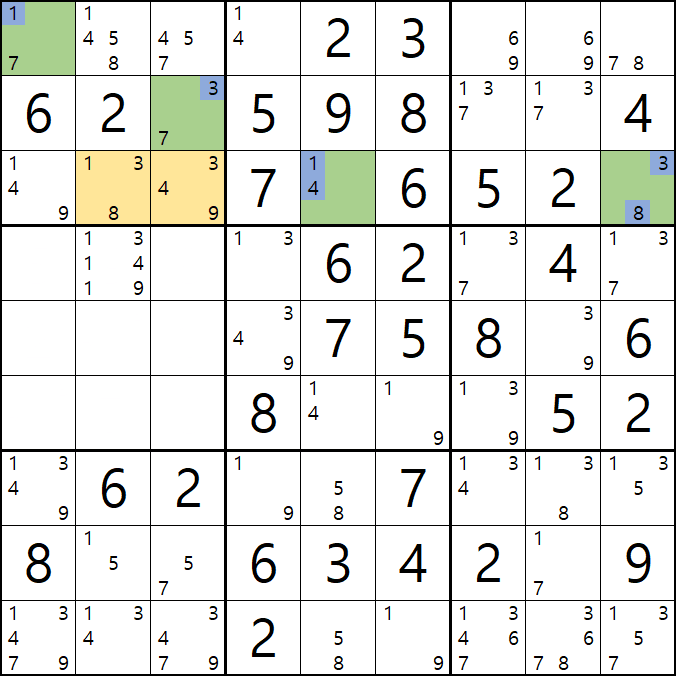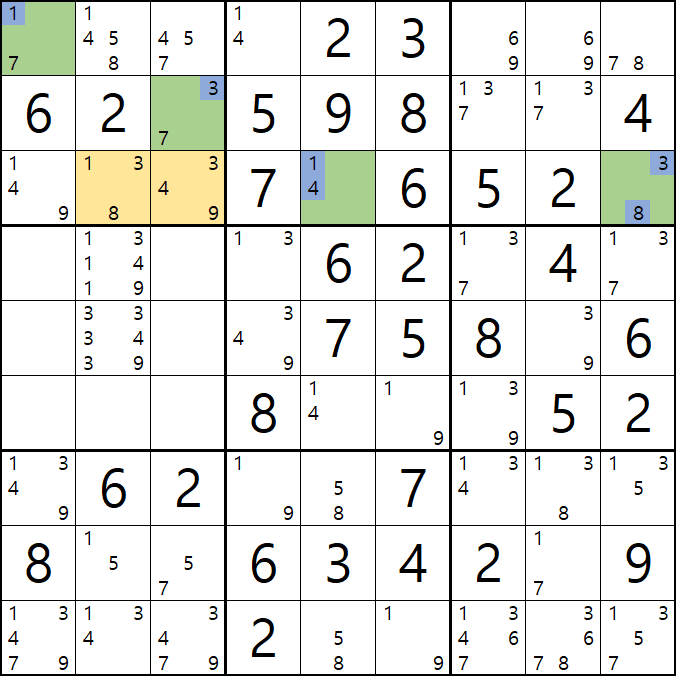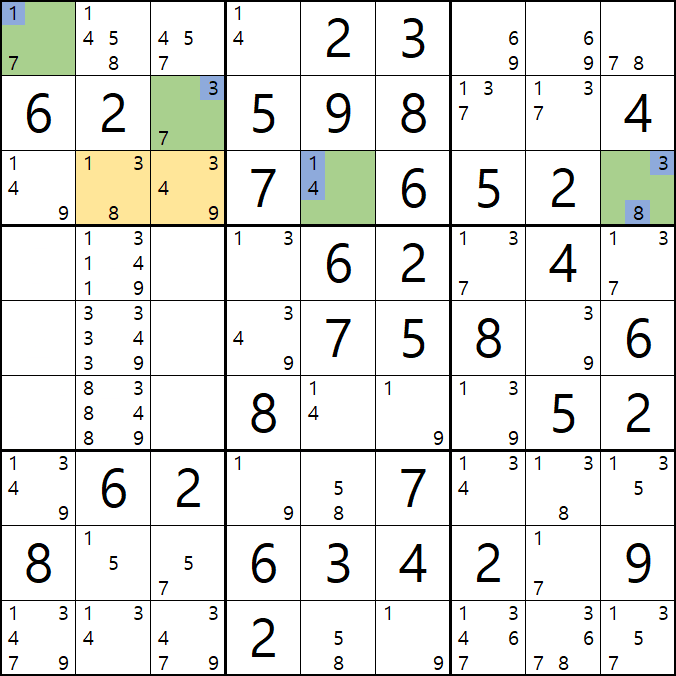
4-3. 

33은 스도쿠 규칙에 위배되는 조합이고

13은 1/7[A1], 3/7[B3] 조합에서 중복이 될 가능성이 잠재되어 있어서 불가능한 조합이 되고

14는 1/4[C5] - 83은 3/8[C9] 와 중복이 되기 때문에 불가능한 조합이 된다. 

 

피벗 칸에서 조합이 가능한 숫자를 살펴 보면 

19 / 34 / 39 / 84 / 89로 C3칸 포지션에는 3이 배제 되는 것을 알 수 있다. 

즉, 3[C3]을 제거할 수 있다. 

 

이상으로 APE TYPE1. 저 세상 레벨 공식을 알아봤다. 일단 어리둥절해도 원리만 이해하자. 나도 꼭 찾으려고 노력하지는 않는다. 그냥 있을 수 있다고만 인지하고, 나~중에는 꼭 찾을 수 있기를 기대한다. 

 

 다만 위의 글을 보고 

1/2 - 1/3 - 1/2/3의 최소한의 숫자로 정렬한다고

세번째 칸의 1을 제거하여

1/2 - 1/3 - 2/3 으로 만드는 우를 범하지 않기를 바란다. 

 

나도 APE를 알기전에 많이 해봤는데, 맞을 수도 있고, 틀릴 수도 있다. APE로 정확히 검증을 해야 

1을 제거해도 될지 않될지 알 수 있는 것이다. 

 

APE가 형성되는 ALS라는 공식을 알면 찾기가 수월해 질 것이다. (이 글에서는 혼선을 초래할까봐 언급은 자제하고 피벗이 되는 칸을 찾는 방법을 설명했는데, 스도쿠는 답이 하나가 아니기 때문에 아래 링크에서 ALS를 익히면 좋겠다.) 

 

움짤로 익히는 스도쿠 18. 거의 잠긴 세트(ALS)

움짤로 익히는 스도쿠 18. 거의 잠긴 세트(ALS)

 

또한 추가로 APE와 비슷한 성질을 갖고 있어서 APE 조건을 갖춘다면 51% 확률로 쉽게 추가 후보숫자를 제거할 수 있는 공식을 알게 됐다. 아래 링크를 꼭 확인하도록 하자!!

 

움짤로 익히는 스도쿠 19. 수-드-콕(Sue-De-Coq)