스도쿠 21. 초고급공식/ 교대 추론 체인(AIC)-움짤, 패턴

싱글로골프
스도쿠/초고급(저세상레벨)
2024. 10. 24.

이번 글에서는 나의 기준으로는 스도쿠의 최종보스인 교대 추론 체인에 대해 알아 보도록 하겠다. 일단 명칭이 익숙하지 않을 텐데 Alternating Inference Chains 라는 명칭을 직역한 것으로 AIC라고도 부른다.

지금까지 알게된 'X체인' 및 '그룹 X체인' 과 XY 체인의 규칙과 동일하지만

한 개의 체인에 위에 기술한 공식이 동시에 나와서 각각의 체인 기술을 교대로 추적하며 체인을 형성한다고

해서 '교대 추론 체인(AIC)'라고 부른다.

자! 최종보스를 잡으러 가보자!!

(참고로 이 글은 최소한 X 사이클, 그룹 링크, XY 체인에 대한 개념은 알고 있다고 가정하고 쓰는 글이다. << 여기서 이야기한 체인공식을 모른다면 아래 링크에서 익힌 후 오길 바란다. 교대 추론 체인이 초고급기술이긴 하지만 잘 나오지 않기 때문에 급한 스도쿠 공식은 아니다.)

예제는 모두 한 개의 게임에 등장하는 여러 개(26개)의 AIC들로 구성됐다. (자료는 '스도쿠 위키' 라는 사이트에서 가져왔다.) 내가 몇 번째까지 만들런지는 짐작이 되지 않지만 최대한 많이 만들어 보겠다는 약한 다짐을...

움짤을 만들다가 살짝 소름이 돋았다. 26개의 AIC 문제 중에서 1~2까지 다른 문제고, 3~23까지 같은 답을 추적하는 문제였다.

12월 10일 추가 > 이 글을 다 쓰고 난 뒤 2달만에 다시 보게 되었는데 이중값 및 삼중값까지 찾아지는 예제였다. 처음에는 이중값만 AIC로 추적하다가 익숙해지면 삼중값까지 도전해 보길 권한다.(나도 아직은 삼중값까지 추적은 힘들다...)

나는 것도 모르고 5번까지 움짤을 만들다가 알게 되었다. 스도쿠 참 대단하다~

그래서 26개 모두 움짤로 만들지 않고, 유형이 좀 다른 것만 추리기로 했다.

그리고 본인의 기존 스도쿠 공식에 대한 이해와 상충되는 개념도 있을 것이다.

그러나 보고 또 보면 이해가 갈 것이라고 믿는다.

(내가 움짤을 만들고 자꾸 보면서 이해하고 있는 중이다.)

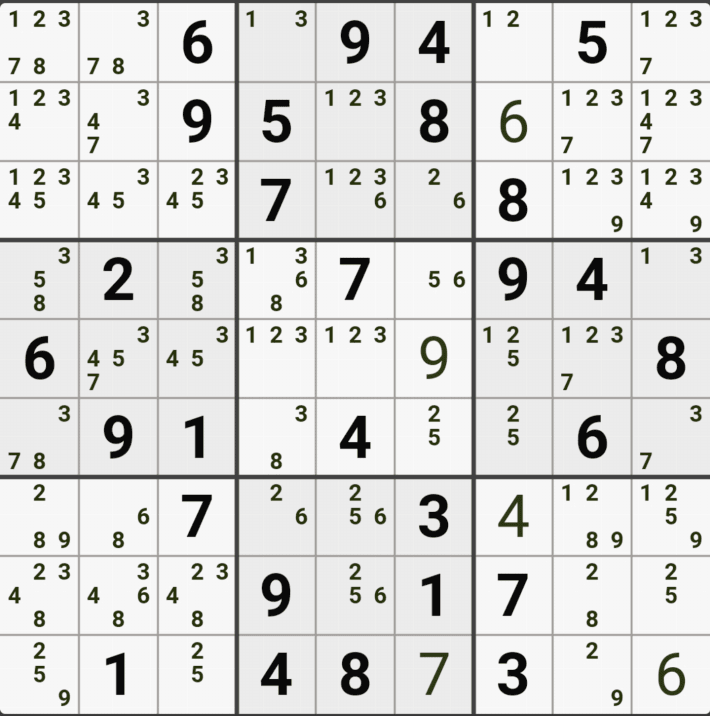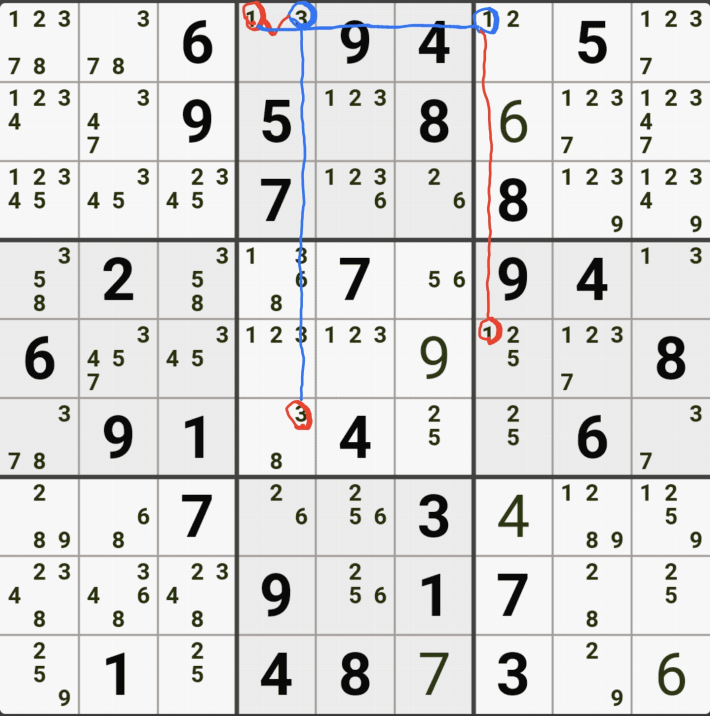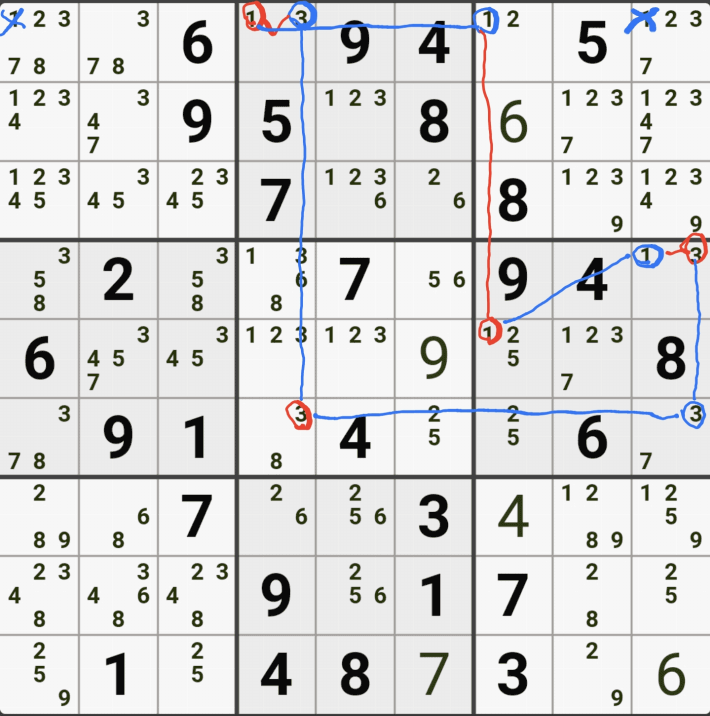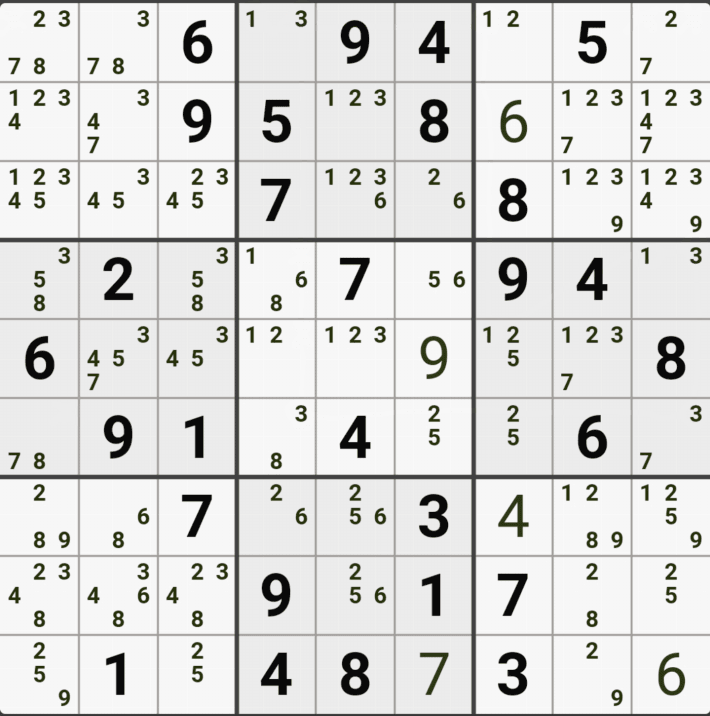
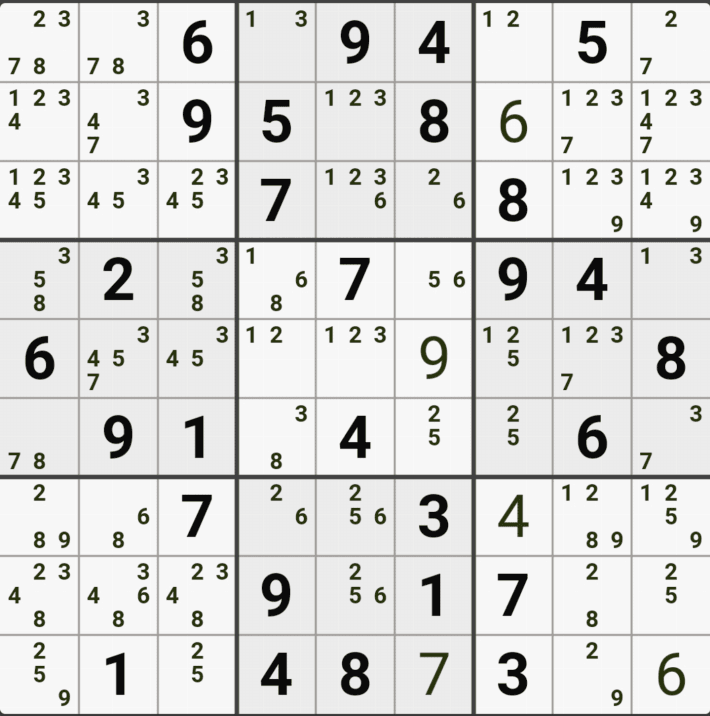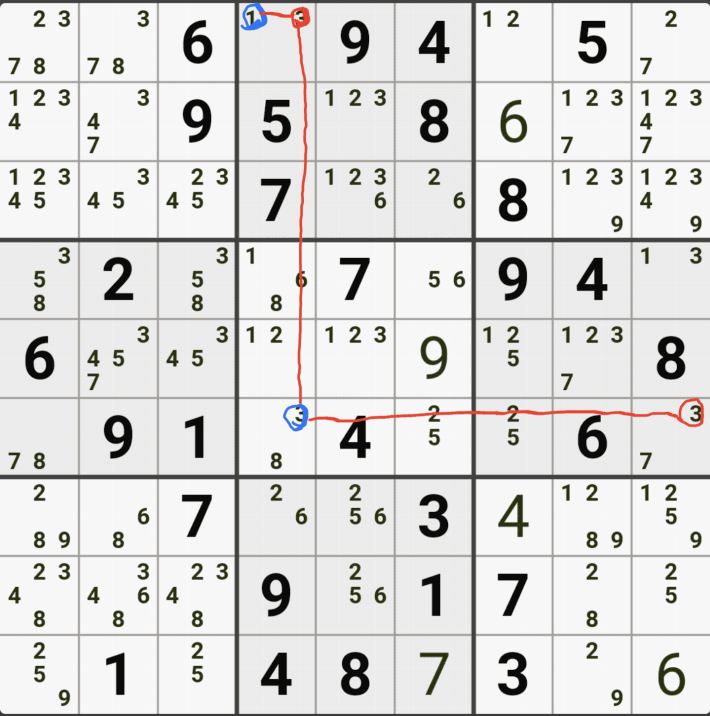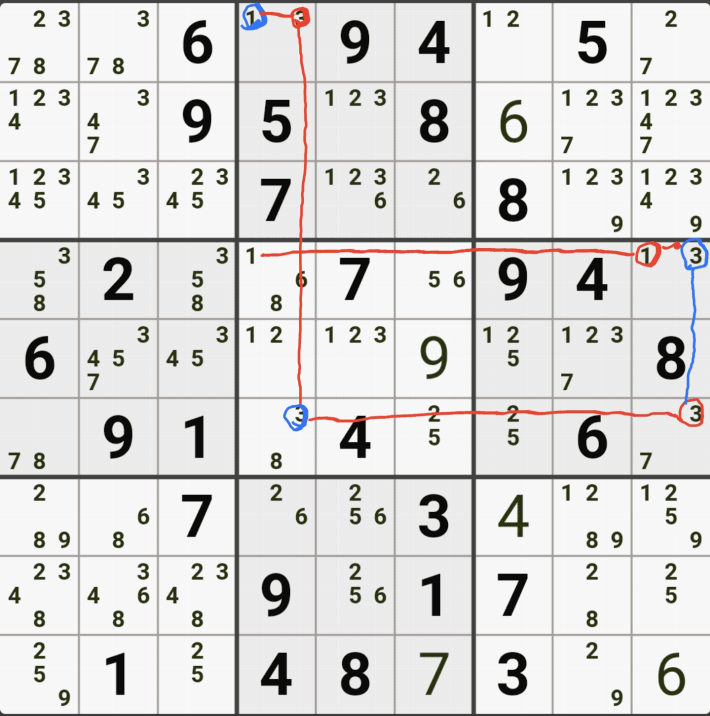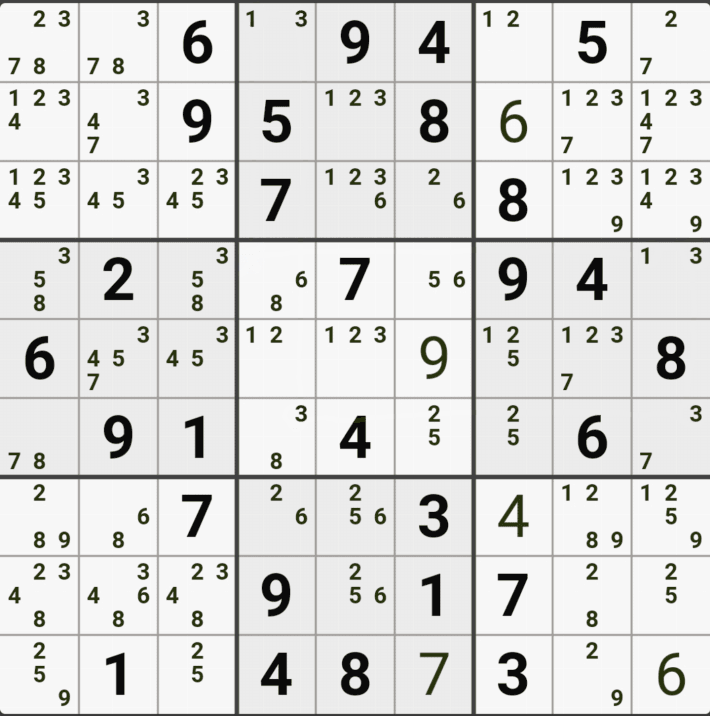
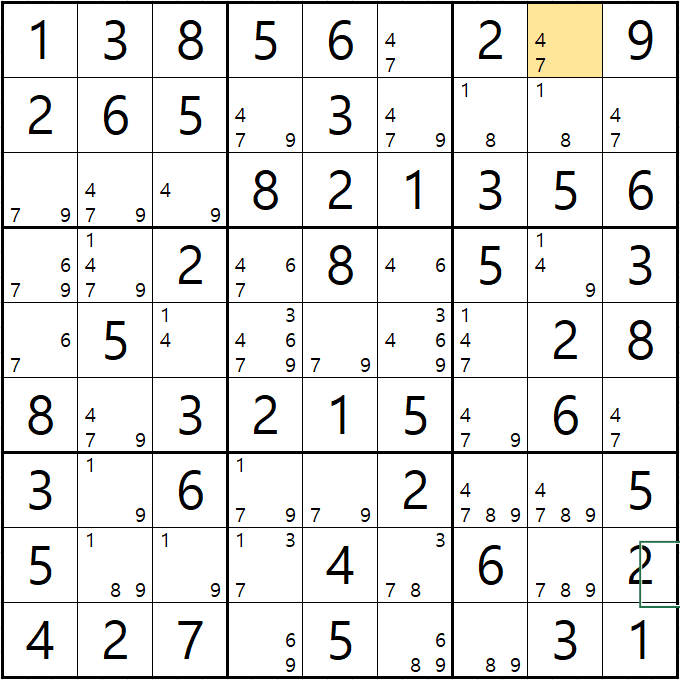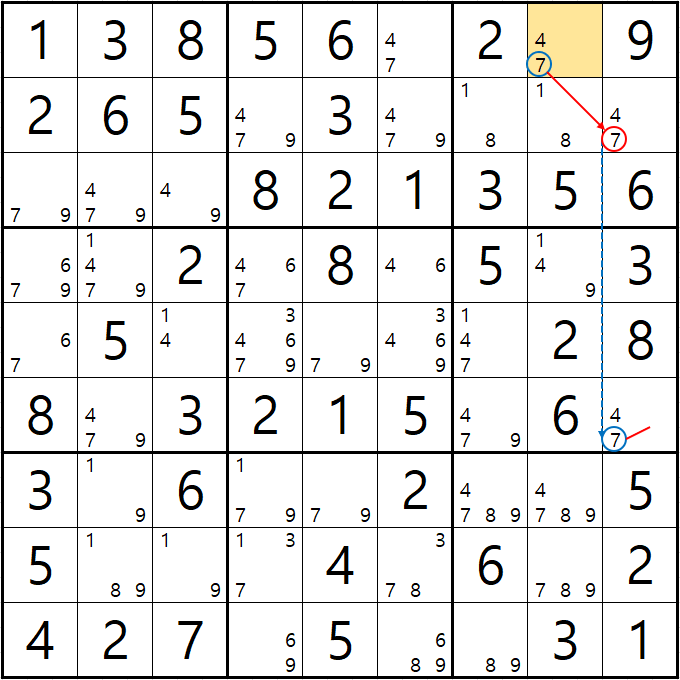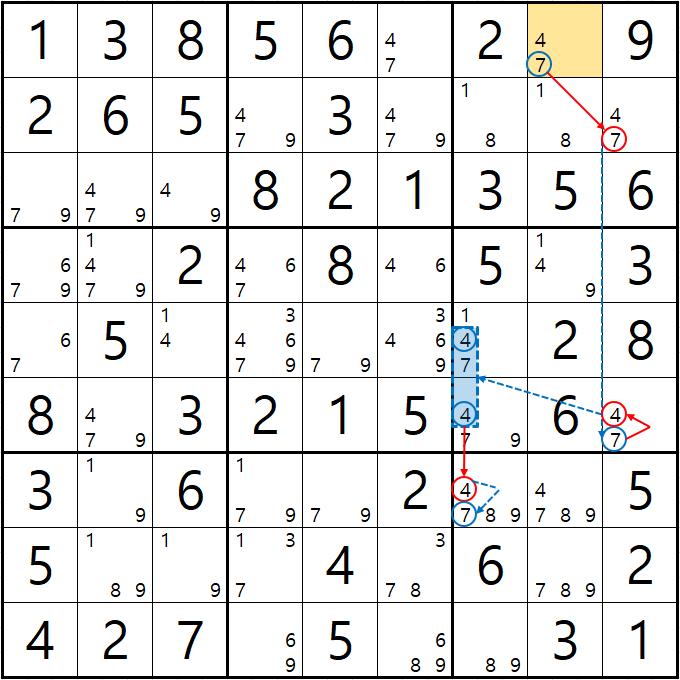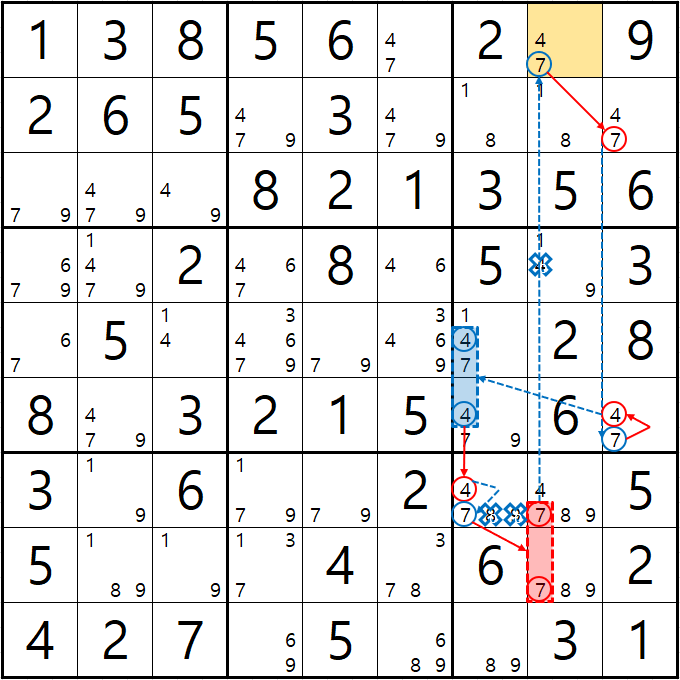
예제 1. 스트롱 링크형 AIC - X체인, XY체인, 그룹체인

-9[F7] +9[F2] -9[G2|H2] +9[H3] -1[H3] +1[G2|H2] -1[D2] +1[D8] -9[D8] +9[F7]

동시에 -9[F2]와 -9[F7]로 F행의 후보숫자 9가 모두 제거되는 모순이 생기므로 F7은 9가 되어야 함 -

따라서, 다른 후보 4/7[F7]은 제거될 수 있음

일단 위의 풀이 개념이 잘 이해가 가지 않는다면 아래에서 X사이클 스트롱 링크형에 대해 알아보고 AIG 스트롱 링크형에 대해 이해하여 보자.

스도쿠 18. 고급공식/ X 사이클(스트롱 링크형)-움짤, 패턴

지난 번 포스팅에서는 X 사이클 (루프형, 위크 링크형) 에 대한 글을 썼다. 스트롱 링크형은 우리가 아는 체인공식과 많이 다르다는 생각과 나의 이해도가 떨어지는지 설명할 길이 없다고 생각했

inoks.tistory.com

예제 2. 스트롱 링크형 AIC - X체인, XY체인, 그룹체인

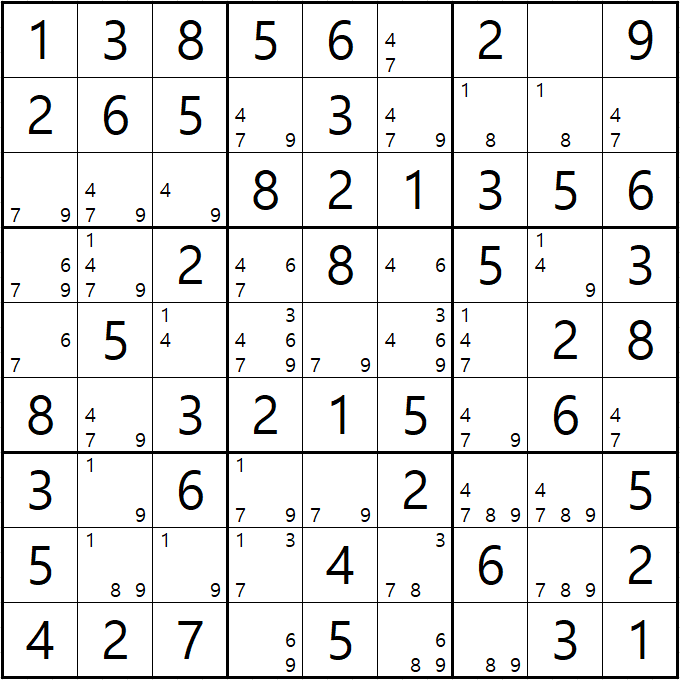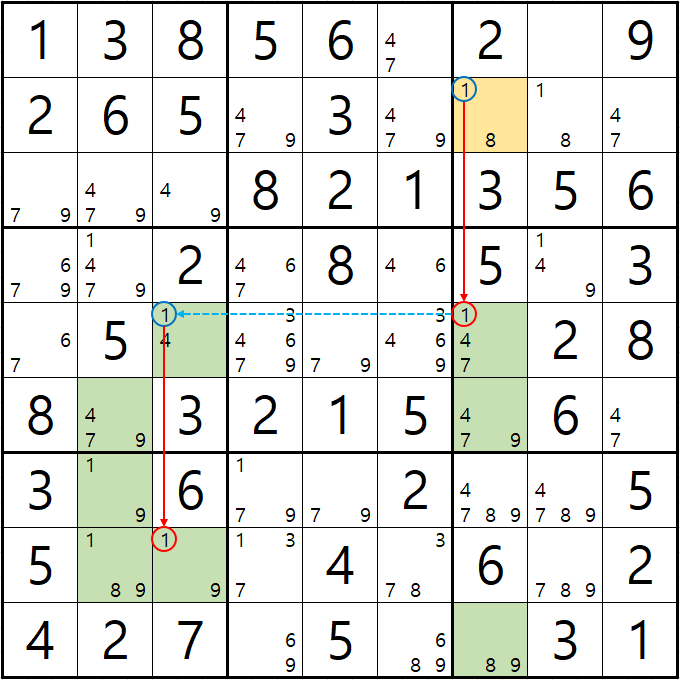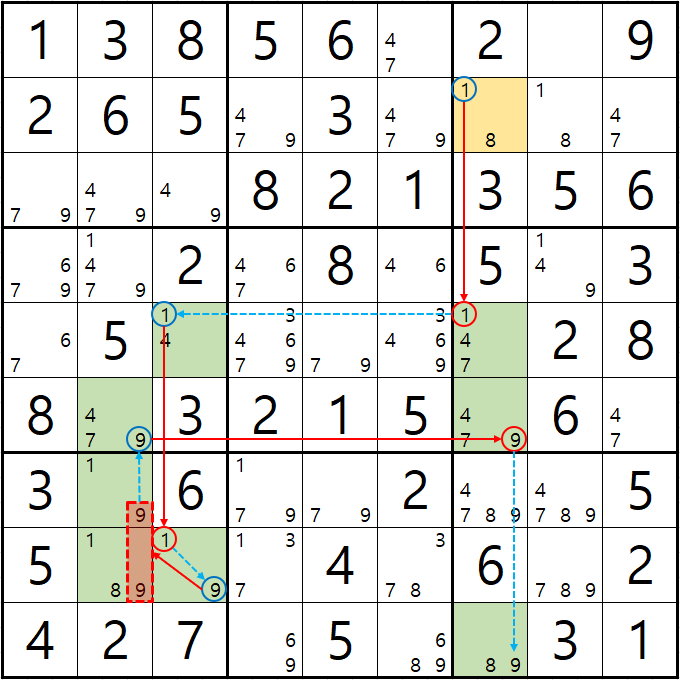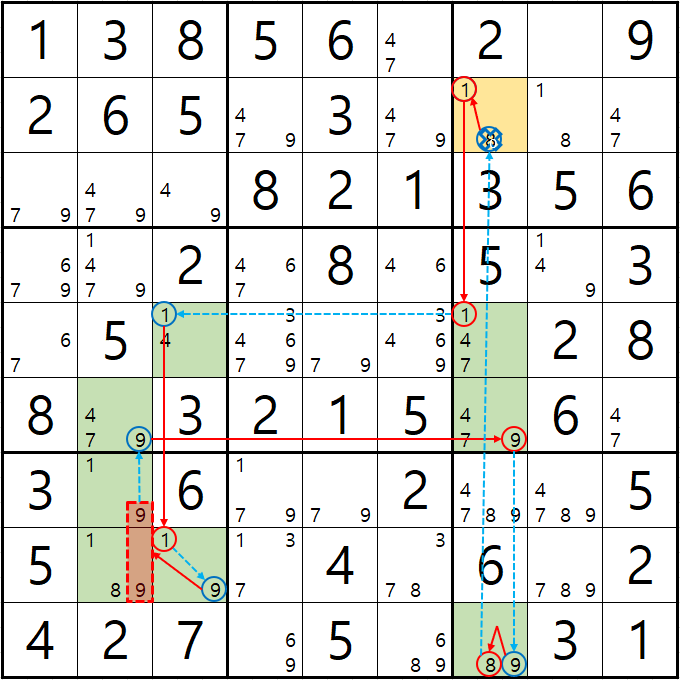
-1[B7] +1[E7] -1[E3] +1[H3] -9[H3] +9[G2|H2] -9[F2] +9[F7] -9[J7] +8[J7] -8[B7] +1[B7]

-1[B7]이 되면 +1[B7]이 되어

처음 가정인 -1[B7]과 모순이 생기므로

처음 명제를 유지하기 위해 후보숫자 8[B7]이 제거 되야한다.

이 다음 글 부터는 답은 같은데 풀어 가는 길이 다른 루프형 AIC 예제 3- 시리즈이다. 익숙해 지는 것이 중요하다고 생각하기 때문에 동일한 형태의 문제에서 어떻게 복합적으로 교대 추론 체인이 조합되는지 보자.

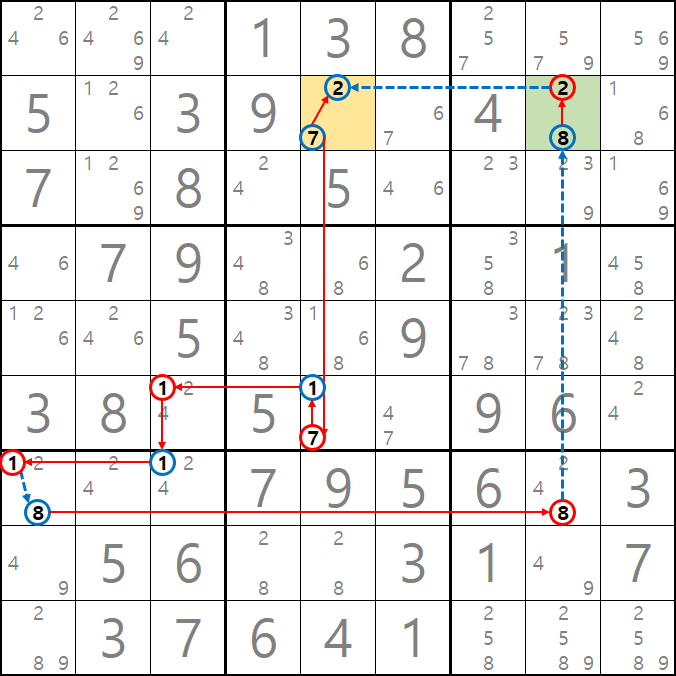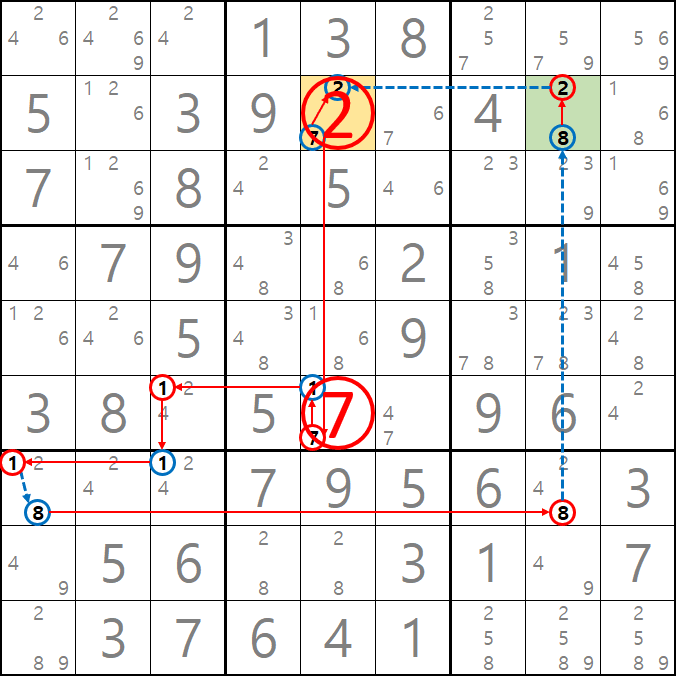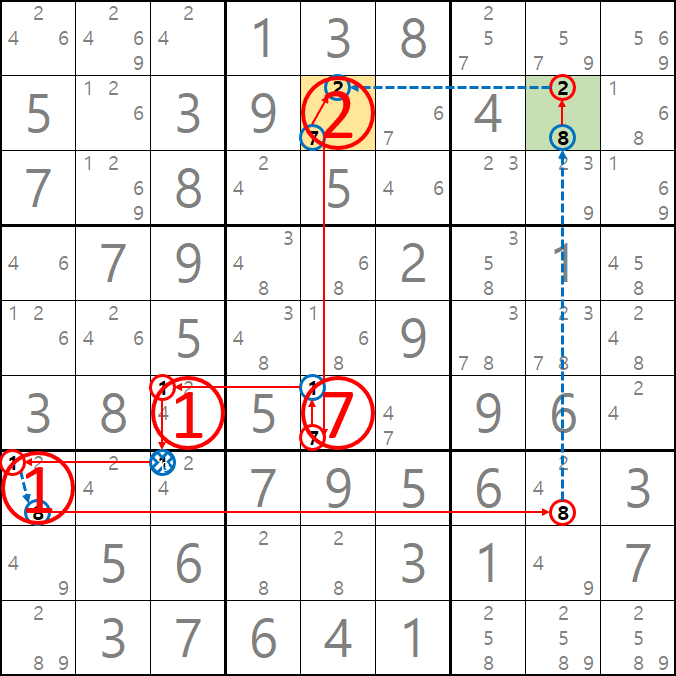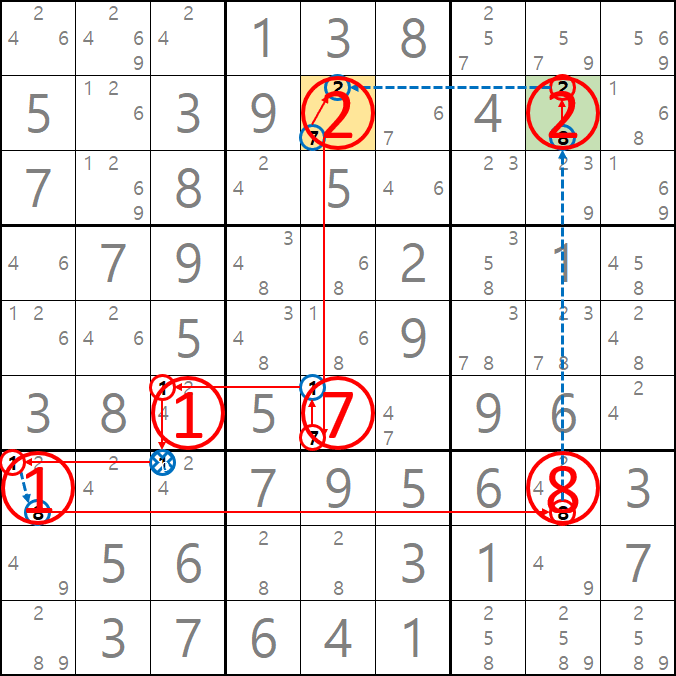
예제 3-1. 루프형 AIC - X체인, XY체인

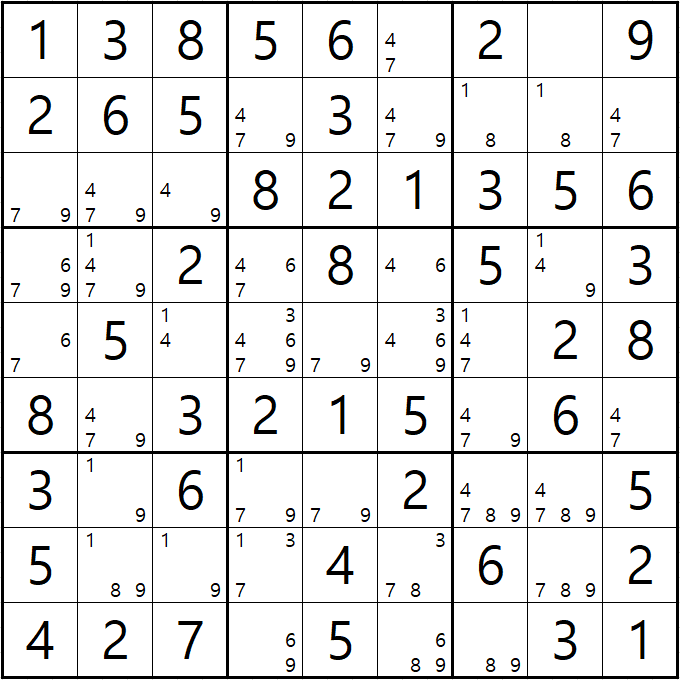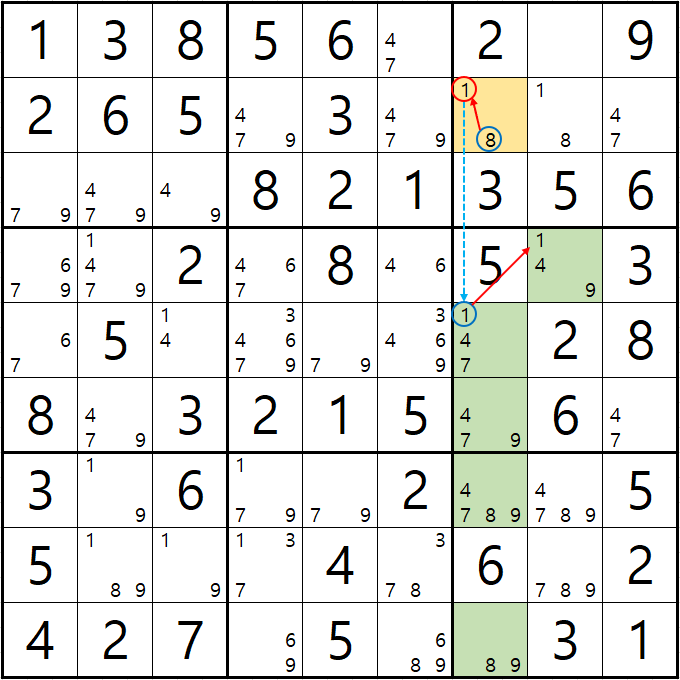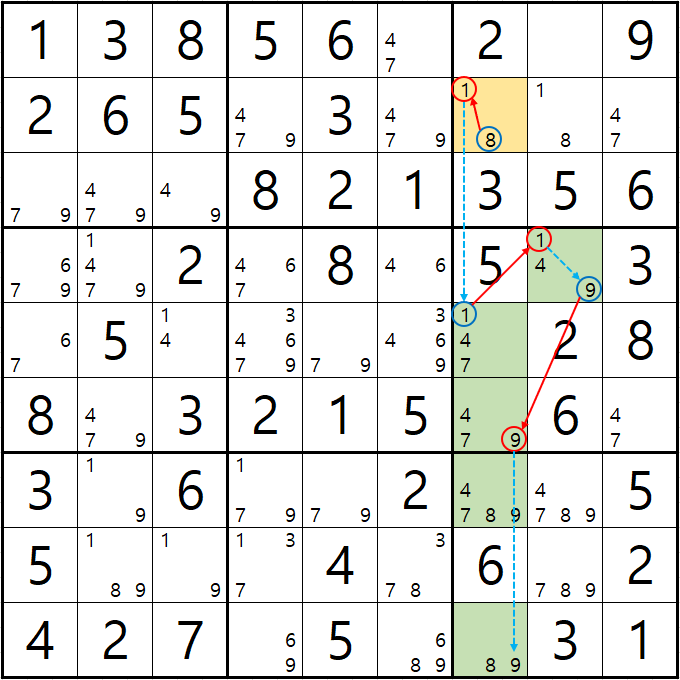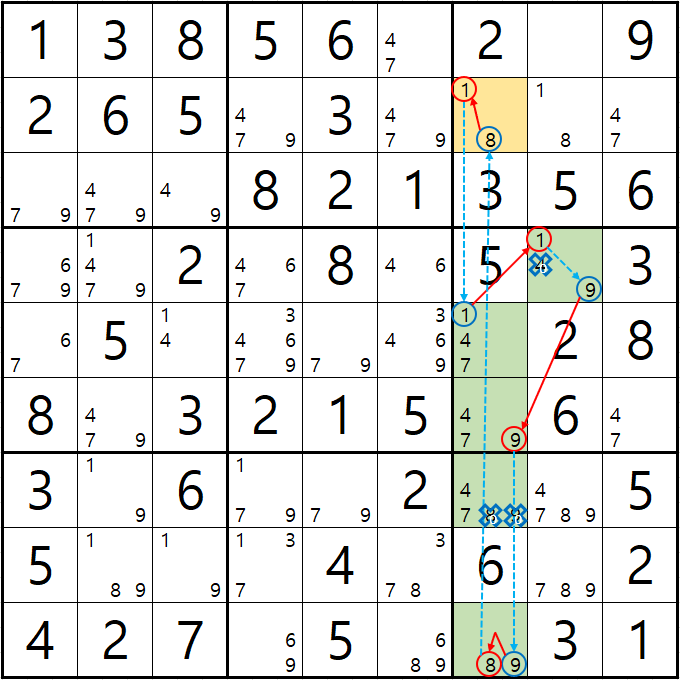
-8[B7] + 1[B7] - 1[E7] + 1[D8] - 9[D8] + 9[F7] - 9[J7] + 8[J7] - 8[B7] 의 루프형 AIC가 완성되어

경로에 들어 있는 후보숫자 4[D8], 8[G7], 9[G7] 3개를 제거할 수 있다.

예제 3-2 루프형 AIC - X체인, XY체인

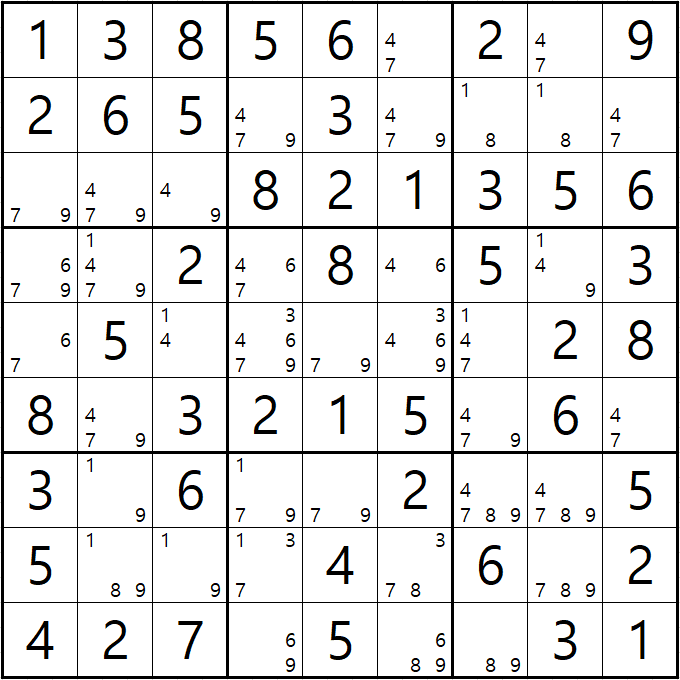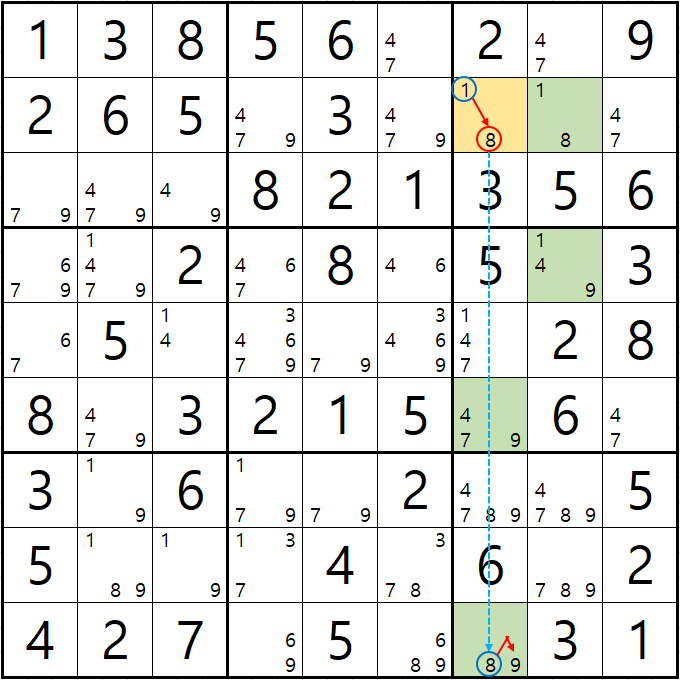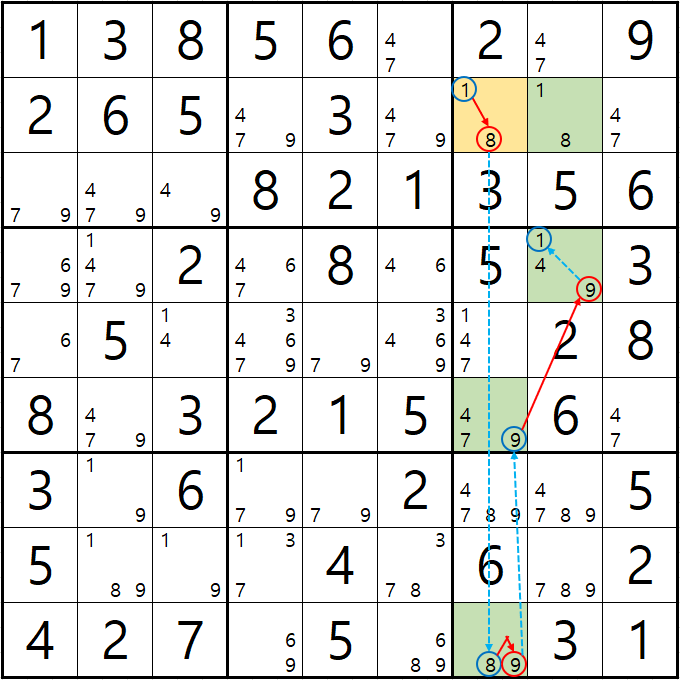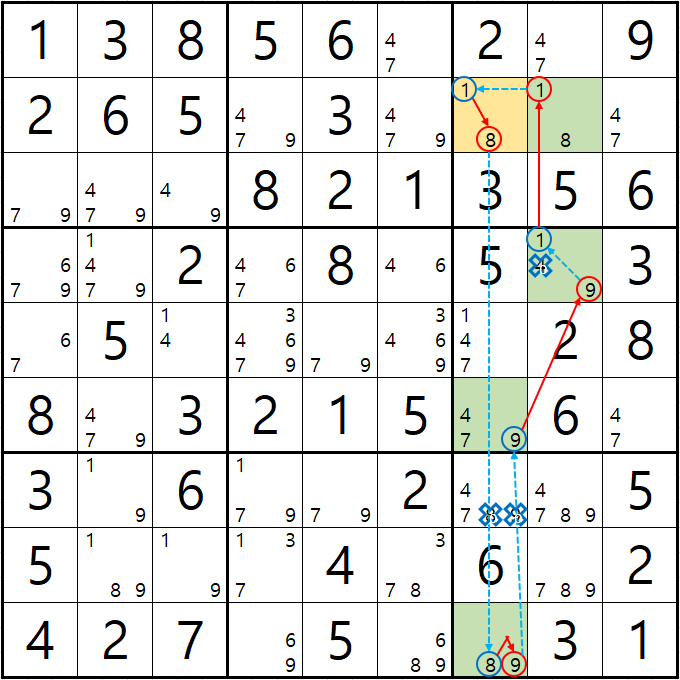
-1[B7] + 8[B7] - 8[J7] + 9[J7] - 9[F7] + 9[D8] - 1[D8] + 1[B8] - 1[B7]의 루프형 AIC가 완성되어

경로에 들어 있는 후보숫자 4[D8], 8[G7], 9[G7]을 제거할 수 있다.

참고로 D8에 후보숫자가 1,4,9가 있는데 9가 off가 된다고 하면 1 또는 4가 되는 것이 아닌가 싶은 사람들이 있을텐데~

후보숫자 1은 D2와 D8에만 있는 이중위치를 갖는 스트롱 링크기 때문에 D8에서 9가 on이 되면 1이 지워질 수 밖에 없다.

예제 3-3. 루프형 AIC - X체인, XY체인

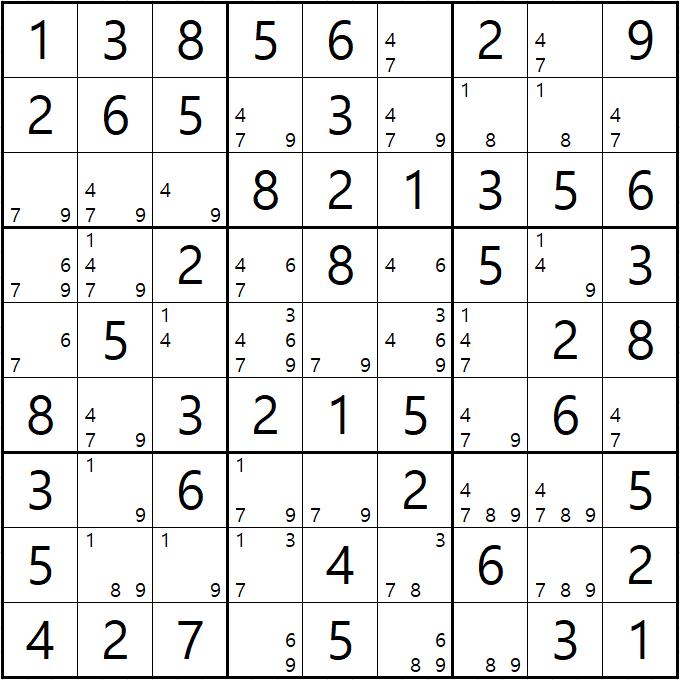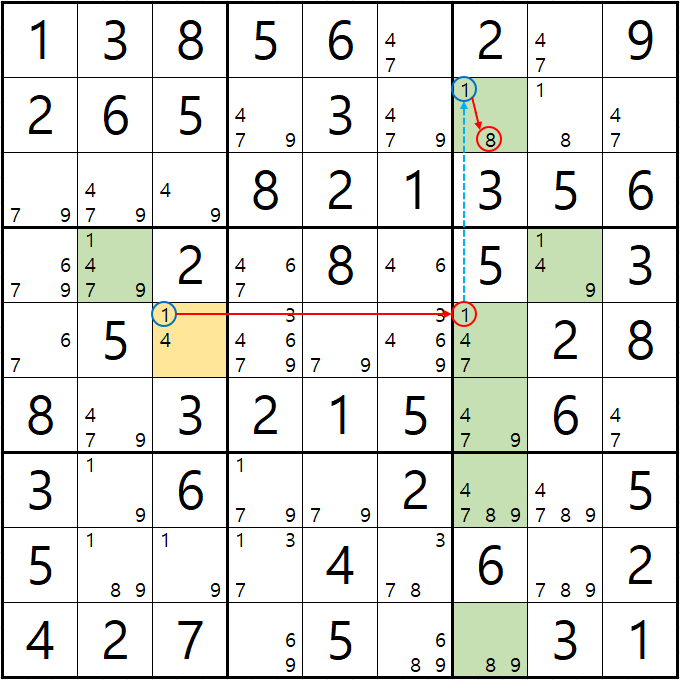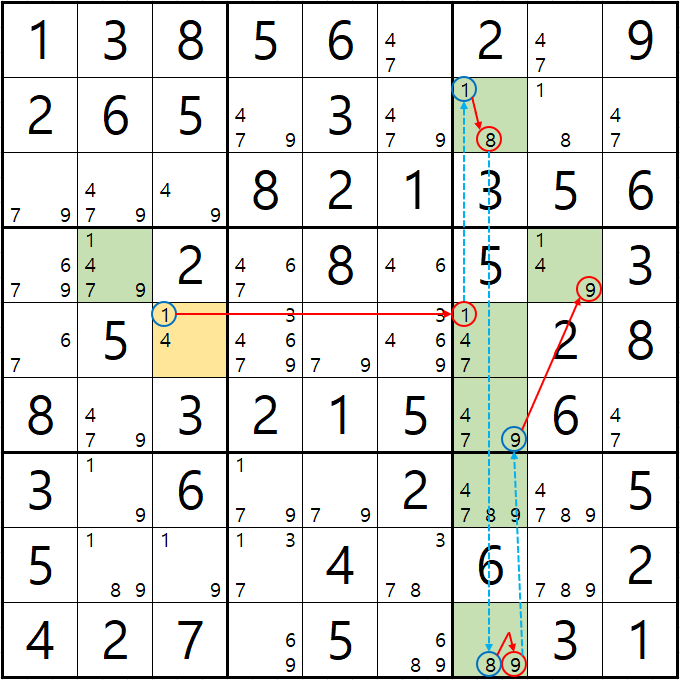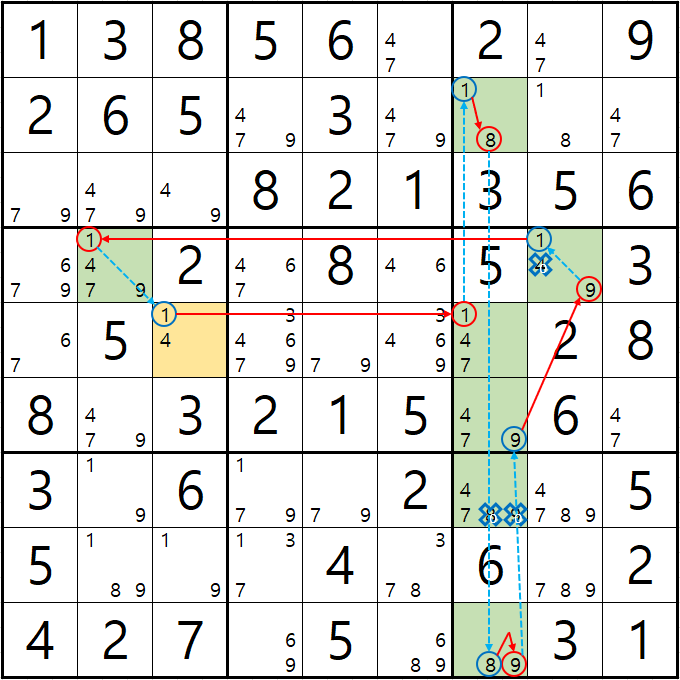
-1[E3] +1[E7] -1[B7] +8[B7] -8[J7] +9[J7] -9[F7] +9[D8] -1[D8] +1[D2] -1[E3]의 루프형 AIC가 완성되어

경로에 들어 있는 후보숫자 4[D8], 8[G7], 9[G7]을 제거할 수 있다.

참고로 D8에 후보숫자가 1,4,9가 있는데 9가 off가 된다고 하면 1 또는 4가 되는 것이 아닌가 싶은 사람들이 있을텐데~

후보숫자 1은 D2와 D8에만 있는 이중위치를 갖는 스트롱 링크기 때문에 D8에서 9가 on이 되면 1이 지워질 수 밖에 없다.

예제 3-4. 루프형 AIC (개인적으로는 제일 재밌는 풀이법이다.) XY체인, 그룹체인

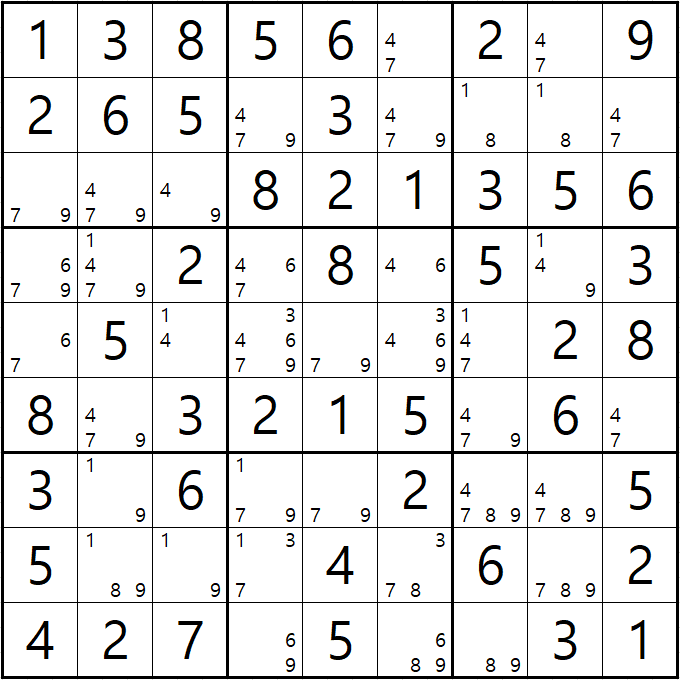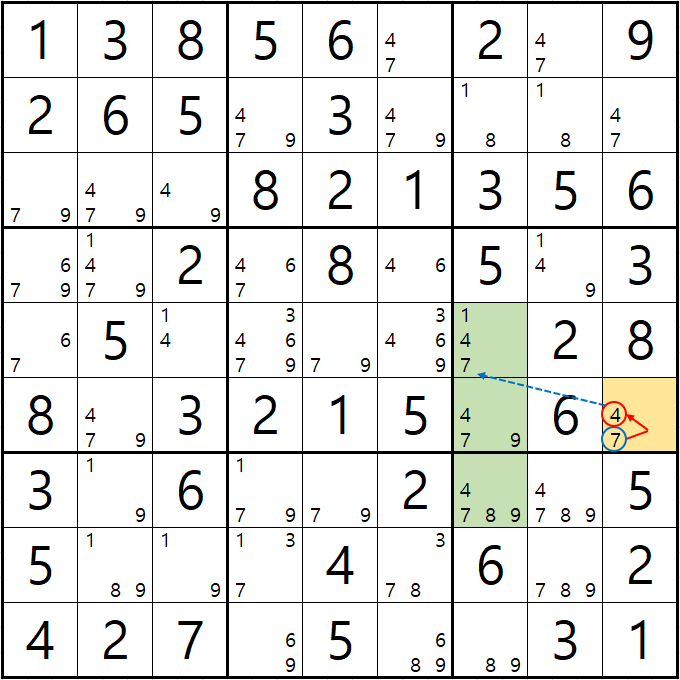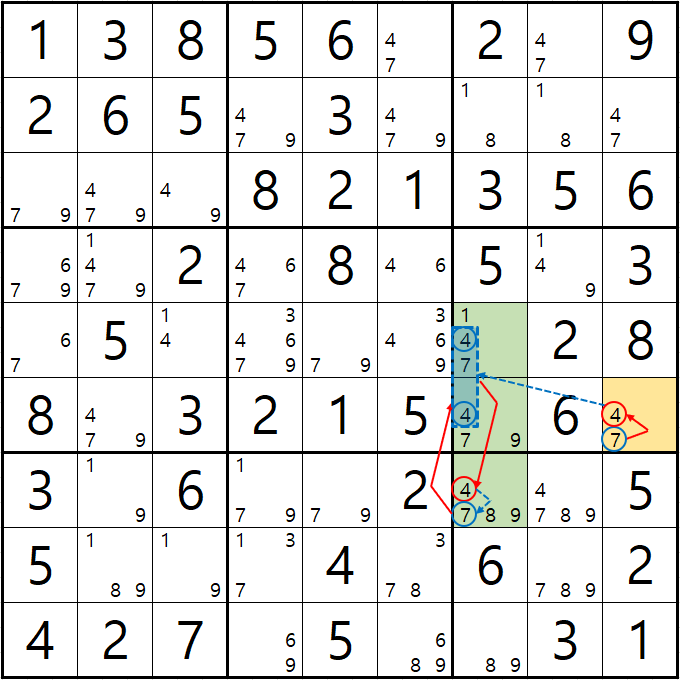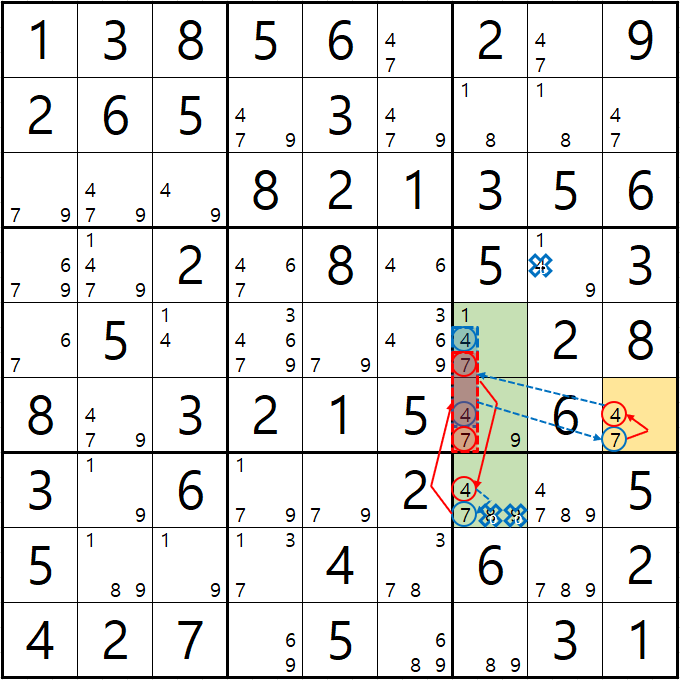
-7[F9] +4[F9] -4[E7|F7] +4[G7] -7[G7] +7[E7|F7] -7[F9] 의 루프형 AIC가 완성되어

경로에 들어 있는 후보숫자 4[D8], 8[G7], 9[G7]을 제거할 수 있다.

예제 3-5. 루프형 AIC - XY체인, 그룹체인

-4[A8] +7[A8] -7[G8|H8] +7[G7] -4[G7] +4[G8] -4[A8] 의 루프형 AIC가 완성되어

경로에 들어 있는 후보숫자 4[D8], 8[G7], 9[G7]을 제거할 수 있다.

예제 3-6. 루프형 AIC (동일 문제 다른 풀이 예제 마지막) XY체인, 그룹체인

11월 24일 추가 > 나도 최근에 알게된 개념은 스트롱 > 위크 > 스트롱 링크 에서 위크 링크는 스트롱 링크로 대체 되어도 문제는 없다는 것이고,

스트롱 링크형 AIC를 좀 더 정확히 설명할 수 있게 되어 추가한다.

아래 짤을 보자.

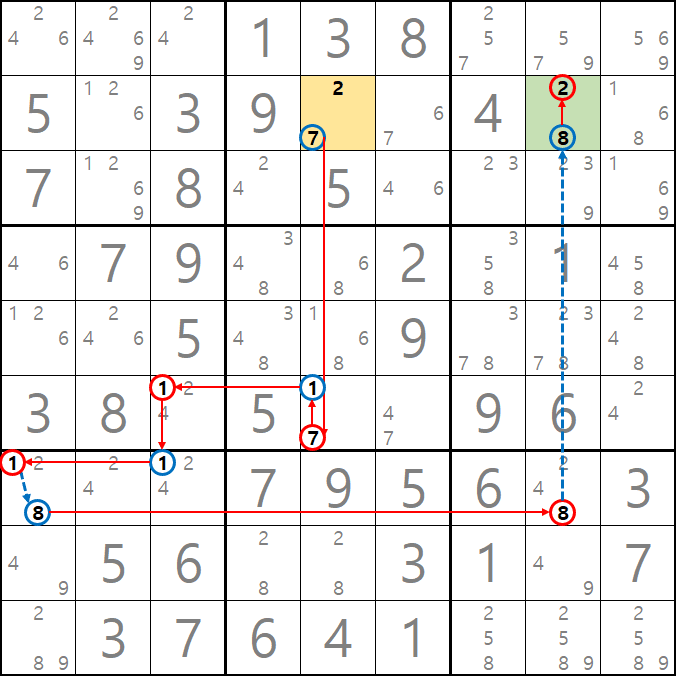
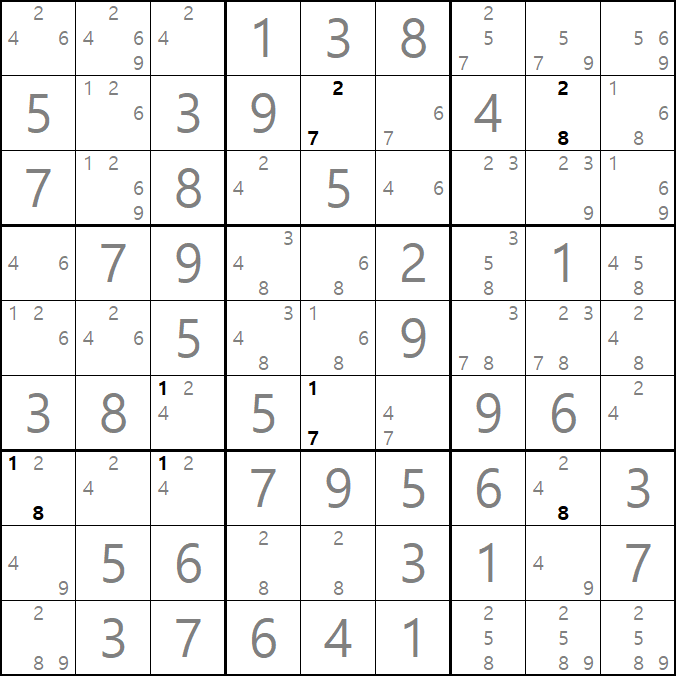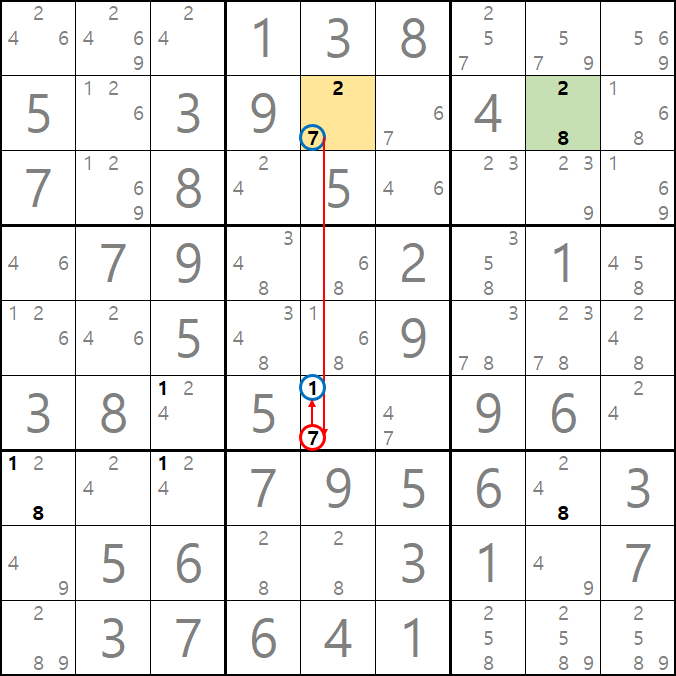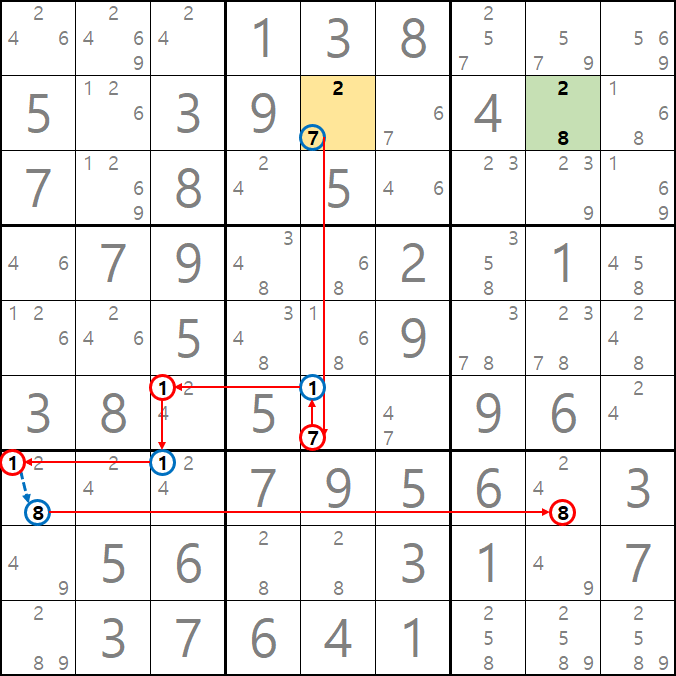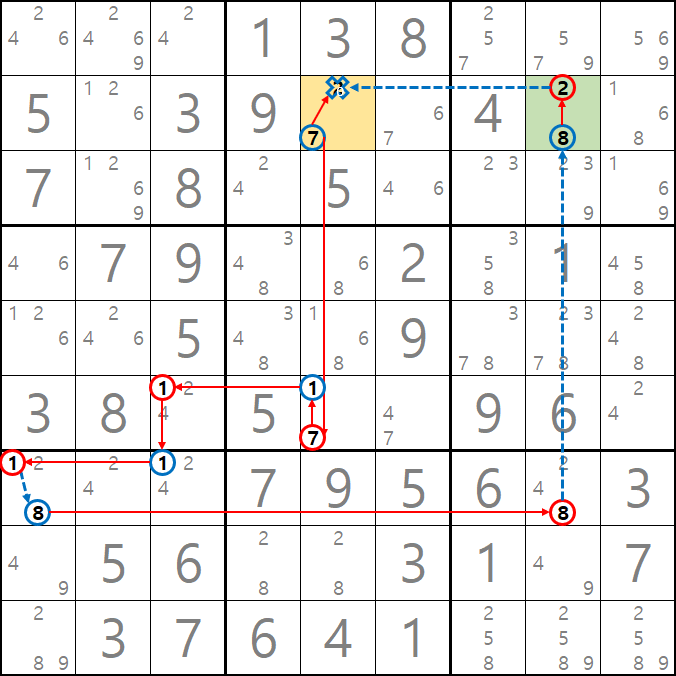
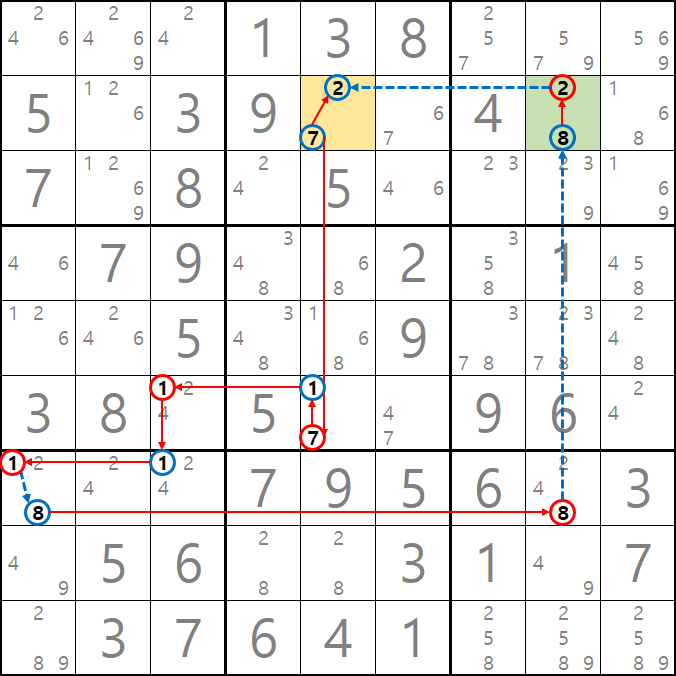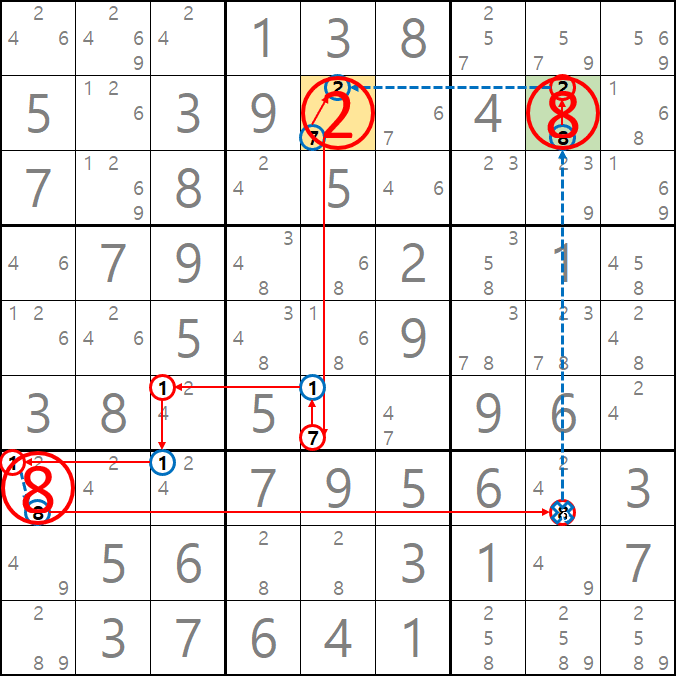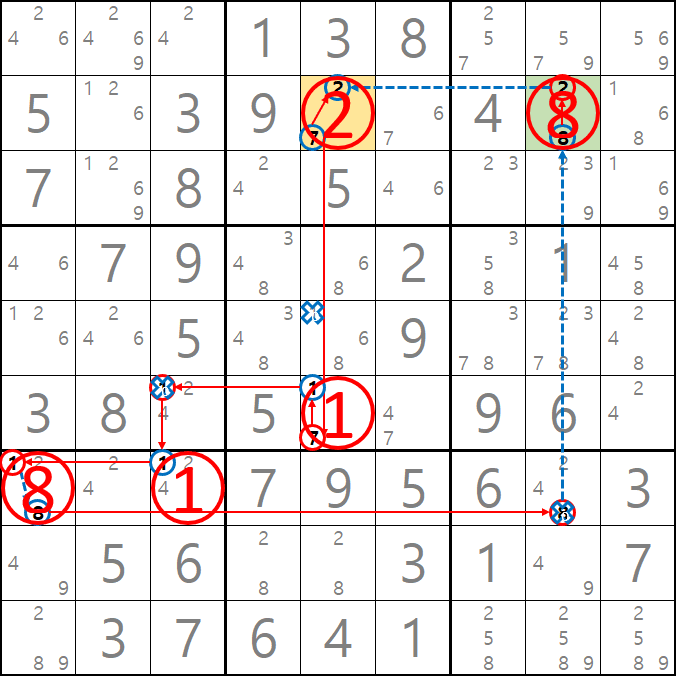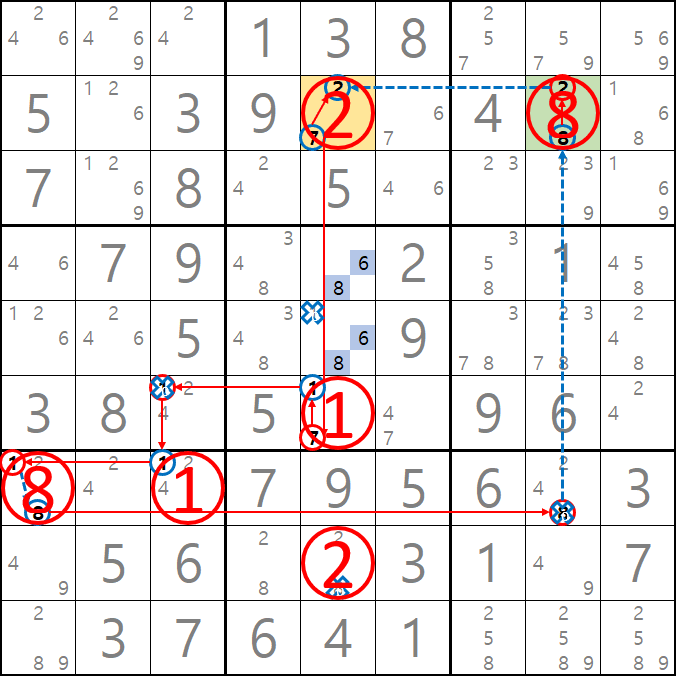
보통 체인으로 후보숫자를 추적할 때 우리는 시작점과 끝점을 동일한 후보숫자 X를 추적하여 시작점과 끝점이 마주보는 후보숫자 X를 제거하는 개념으로 접근해왔다. 그래서 위의 움짤을 보면 열심히 체인을 형성했지만 해를 찾지 못하는 아쉬운 상황으로 보일 수 있지만

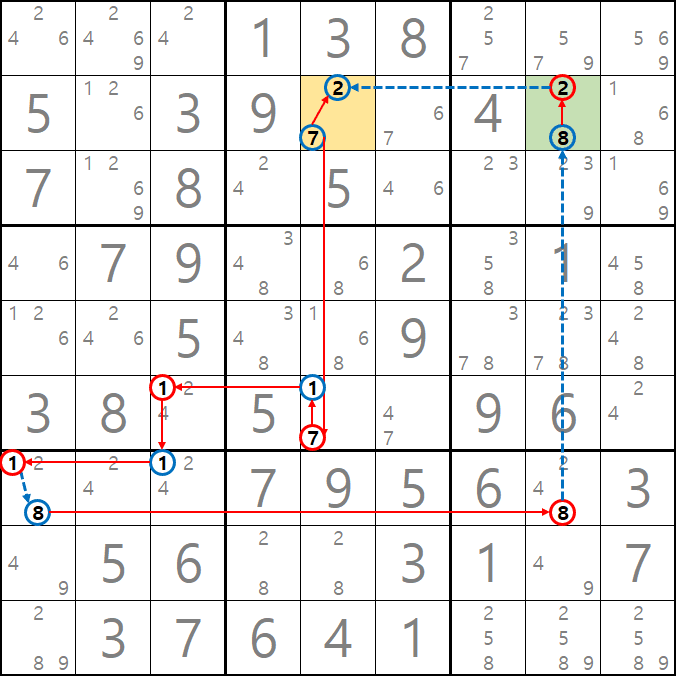
체인을 끝까지 연결하면 위의 짤과 같이 -7[B5]과 -2[B5]가 되어 B5칸의 후보숫자 모두 OFF가 되는 모순이 생기는 것을 알 수 있다. 따라서 이런 모순을 제거 하기 위해서는 -2[B5]가 삭제 되어야 한다.'는 결론을 얻을 수 있다.

즉 체인으로 연결되는 경우 숫자가 달라도

ON이 되는 후보숫자 X와 OFF가 되는 후보숫자 Y가

마주보는 후보숫자 X 또는 Y를 제거할 수 있다는 것이다.

위의 짤을 움짤로 보면 아래와 같다.

이를 텍스트로만 이해하자면

-7[B5]+7[F5]-1[F5]+1[F3]-1[G3]+1[G1]-8[G1]+8[G8]-8[B8]+2[B8]-2[B5]에서 링크를 한 번 더 추가하면 +7[B5]가 되어

-7[B5] 시작점과 +7[B5] 끝점에서 동일한 후보숫자에 동시에 발생하는 (즉, 답이 없는 모순이 생기므로

또한 위의 결론을 얻는 다른 방법은 '스트롱 링크형 AIC라는 점이다.

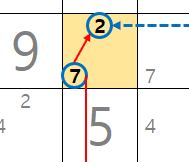
시작점인 -7[B5] 이

2번째 링크과 마지막 링크가 모두 스트롱 링크가 둘러쌓여 있기 때문에 -7[B5]이 해가 되는 것을 알 수 있다.

혹시 이해가 되지 않으면 아래 짤을 스케치 앱을 열어서 직접 선을 2~3번 그어보면 바로 이해가 될 것이다.

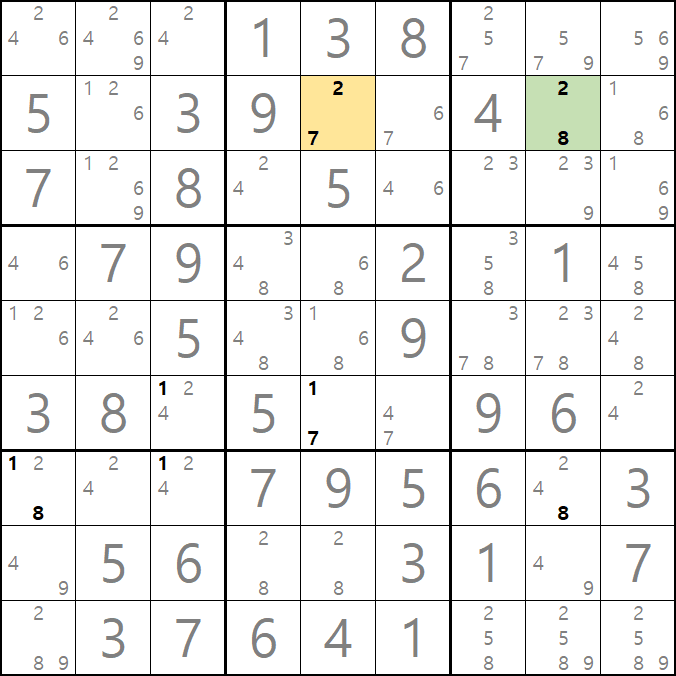
또한~ 만약에 D5가 2가 된다면 아래와 같이 2가지의 모순이 생기기 때문에 해가 아니다.

D5가 2가 된다면 D8도 2가 되는 모순이 생긴다.

그럼 시계방향으로 돌면 달라질까? 당연히 아니다. 스도쿠는 1개가 틀어지면 모두 틀어진다.

아래 움짤과 같이 5열에 후보숫자 7이 모두 지워지는 모순 1개와 2가 2개 존재하는 모순 1개, 총 2개의 모순이 발생한다.

나도 사족을 계속 다는 것은 매우 귀찮다. 그래도 올리는 것은 그 만큼 스트롱 링크 개념이 주요하기 때문이고, 나와 같이 스도쿠를 좋아하는 스도커들의 실력이 한 단계 더 올라가기를 바라기 때문이다~

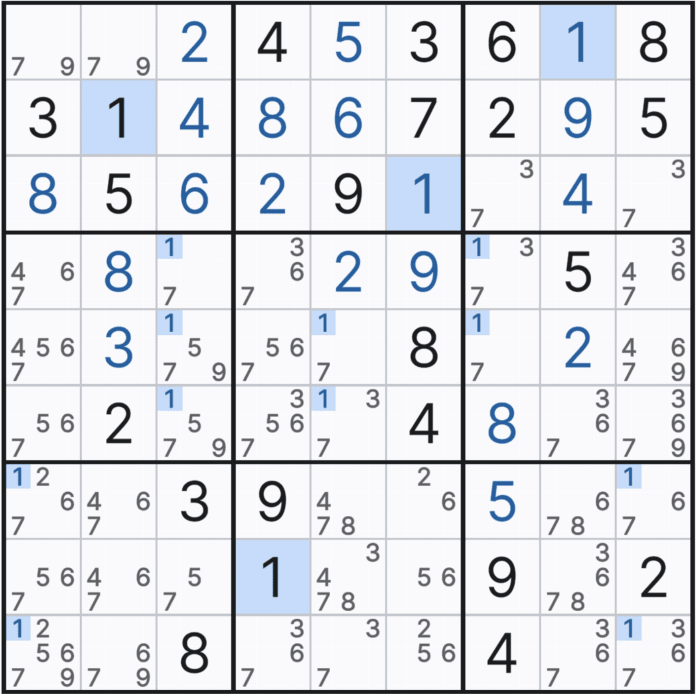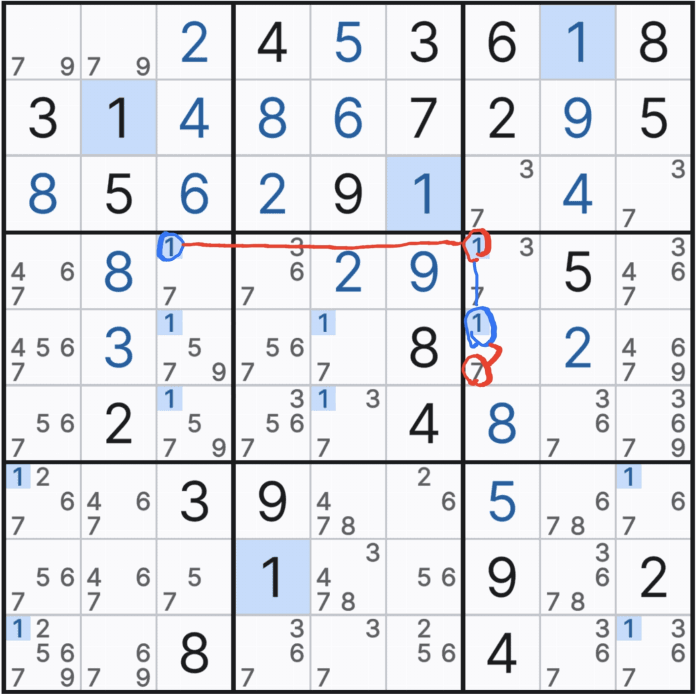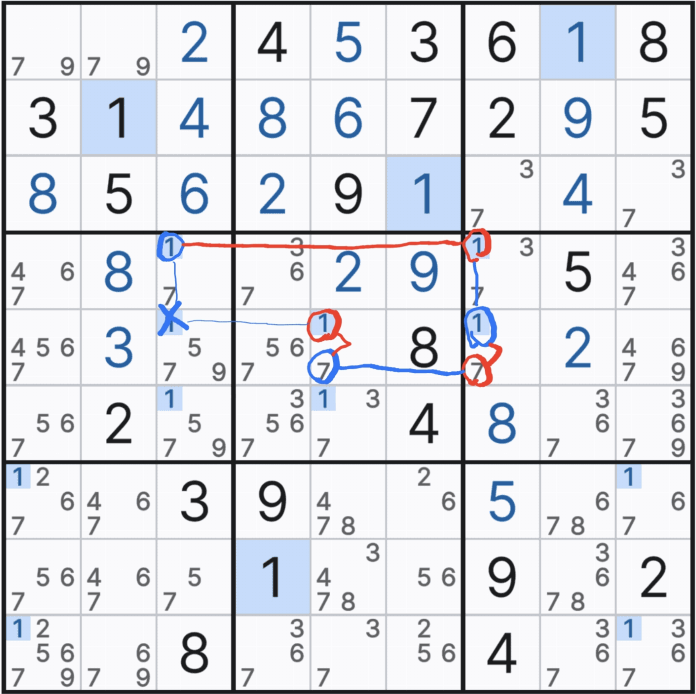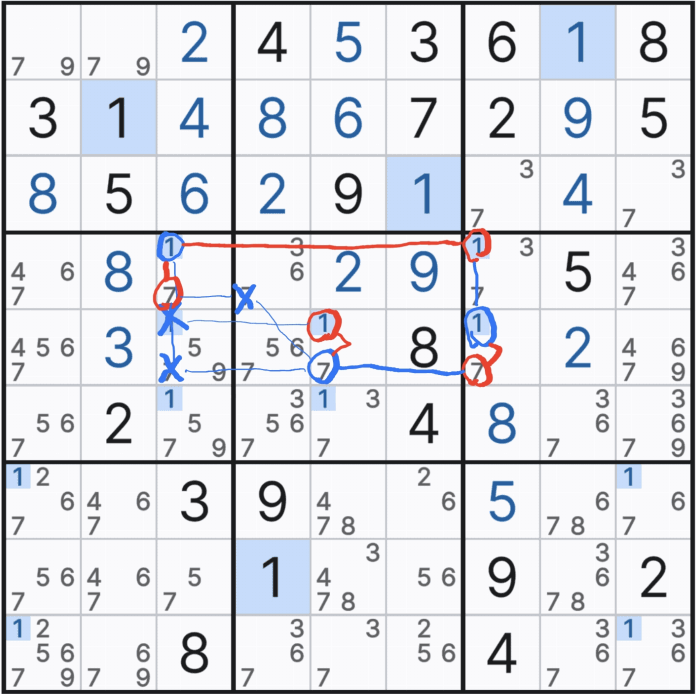
10월 26일 추가 > 무작정 교대 추론 체인을 적용하기 보다는 아래 움짤처럼 X체인으로 출발해서 링크가맞지 않을 때, 한개의 링크만 깨면 될 거 같을 때, XY 체인을 적용해 보기를 권한다.

조금 더 심화학습을 하기 위한 스도커를 위해서 '스도쿠 위키'라는 사이트에서 위의 움짤 예제를 포함한 약 50개의 다이아그램을 캡쳐해서 올린다. 아래의 '더 보기'를 클릭하면 된다. 순서는 루프형, 위크 링크형, 스트롱 링크형 순이며 그 안에서도 링크수가 적은 것 부터 오름차순이 되고, 그룹링크가 있다면 다시 링크수가 적은 것부터 오름차순이 된다.

간단히 다이아그램을 설명하자면