스도쿠 16. 고급공식/ X 사이클(루프형, 위크링크형)-움짤, 패턴

싱글로골프
스도쿠/고급
2024. 10. 7.

이번 글에서는 스도쿠 고급 공식인 X 사이클 체인(=X Cycles)에 대해 알아 보도록 하겠다. X 사이클은 명칭에서 알 수 있듯이 하나의 후보숫자 X를 체이닝 했을 때 모든 하우스에서 링크가 순환하는 연결 형태의 체인을 이야기 한다. 싱글 체인과 X 체인 모두 X사이클 체인의 조건부 하위 개념으로 보면 되겠다.

일단 X사이클 체인은 자주 나오지 않는다.

스도쿠 입문자라면 굳이 찾으려 애쓰지 말자.

중급자더라도 종반에 확실한 페어 및 트리플 지옥에 빠졌을 때 검토하는 것을 추천한다.

단계를 1~5로 봤을 때, 4~5단계는 자주 출현한다.

X사이클은 크게 3가지의 유형이 존재하는데...

1. 루프형(Loop) - 후보수를 모두 연결 시키면 스트롱 링크가 되며, 닫히는 모양의 완전한 루프 사이클을 이루는 체인으로

모든 경우에 수에서 언제나 같은 똑같은 결과값을 내는 특징을 가지고 있다. (단, 규칙으로 좌측 상단을 시작점으로 본다.)

루프를 이루는 링크의 갯수는 언제나 짝수의 갯수로 이루어 진다.

루프로 연결된 모든 링크에서 행과 열로 직선을 그었을 때 속하는 후보수 X를 전부 제거 할 수 있다.

폐쇄되는 형태가 되기 때문에 Off-Chain이라고도 칭하기도 한다.

다른 체인 기술들은 수고에 비해서 지울 수 있는 후보숫자는 1개인데 반해서 루프형은 최소 1개 이상 찾을 수 있는 지뢰 찾기로 보면 2~10 개를 한 번에 터트리는 효과가 나오는 스도쿠 기술이다.

우리가 익히 아는 엑스윙 또는 2x2x2 소드피쉬는 X사이클(루프형)을 정형화 시킨 명칭으로 보면 된다.

2. 위크 링크형(Weak Link) - 시작점과 끝점에서 동시에 바라보는 칸의 후보수 X를 제거 할 수 있다.

단, 시작점과 끝점에서 마주보는 칸은 모두 위크 링크로 연결이 된다.

링크를 연결할 때는 스트롱(시작점) > 위크(스트롱 대체가능) > .... >스트롱(끝점)의 형태가 되며 후보숫자의 갯수는 홀수개이다.

위의 말이 의미하는 것은 시작점과 끝점을 바꿔도 결과는 같아야 한다는 뜻이다.

이 때, 후보수가 제거되는 칸까지 연결하면 불완전한 루프의 형태를 갖는다.

X-Chain이라고도 불리운다.

싱글체인(=심플 컬러링)과 형태는 유사하나 디테일한 부분에서 다른점 한 가지는 싱글 체인은 스트롱 링크로만 연결되는데 반해서 X사이클(위크 링크형)은 스트롱 > 위크 >....> 스트롱 링크로 연결된다는 것이다. 즉, 싱글 체인이 X사이클의 하위개념으로 보면 되겠다.

시작점에서부터 스트롱 링크로만 연결 되는 싱글 체인과 스트롱+위크 링크가 혼재되는 X체인은 엑스사이클의 한 형태이다.

3. 스트롱 링크형(Strong Link) - 위크 링크형과 형태는 똑 같아 보이는 링크지만 시작점과 끝점에서 동시에 바라보는 칸은 스트롱 링크로 연결되고 후보수 X가 확정숫자가 된다는 것이 크게 다른 점이다. 또한 링크의 숫자가 홀수개로 연결되는 불완전한 루프형태가 된다.

위와 같이 3가지 형태가 있는데 이번 글에서는 1.루프형(Loop) 2. 위크 링크형(Weak Link)에 대해 알아 보겠다. 3.스트롱 링크형 엑스 사이클은 공식대로는 설명을 해 줄 수 있는데, 왜 그렇게 되는지는 아직 이해를 못했다.

10월 22일 추가 > 스트롱 링크형 X 사이클에 대해 설명할 수 있게 되서 글을 새로 썼다. 아래 링크 확인요~

스도쿠 18. 고급공식/ X 사이클(스트롱 링크형)-움짤, 패턴

지난 번 포스팅에서는 X 사이클 (루프형, 위크 링크형) 에 대한 글을 썼다. 스트롱 링크형은 우리가 아는 체인공식과 많이 다르다는 생각과 나의 이해도가 떨어지는지 설명할 길이 없다고 생각했

inoks.tistory.com

자 일단은 위의 글만 읽고는 감이 잘 오지 않을 것이다.

아래는 박스'안에 나타나는 각 후보숫자별 스트롱, 위크링크를 표기한 움짤이다. 스트롱 링크야 직관적으로 보이니까 위크 링크의 형태를 집중해서 보자. 고급 체인 기술로 갈 수록 스트롱 링크와 위크 링크의 역할이 매우 중요해 진다.

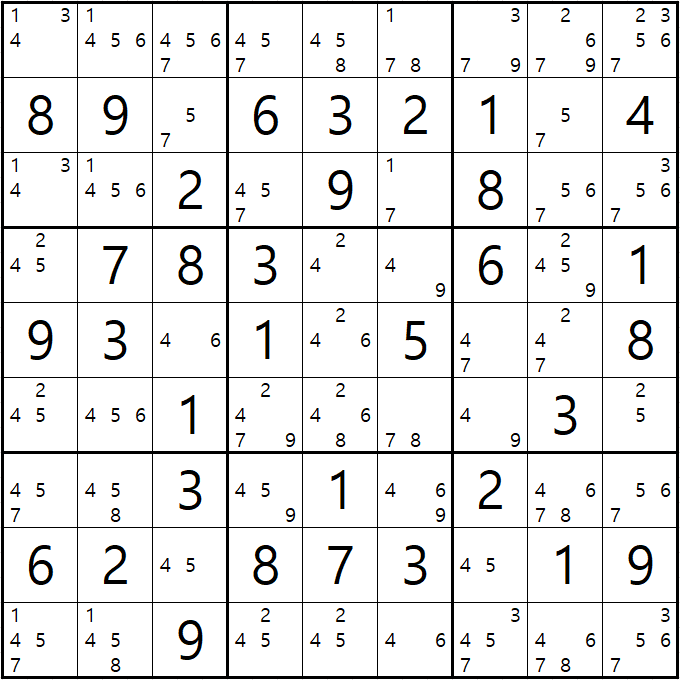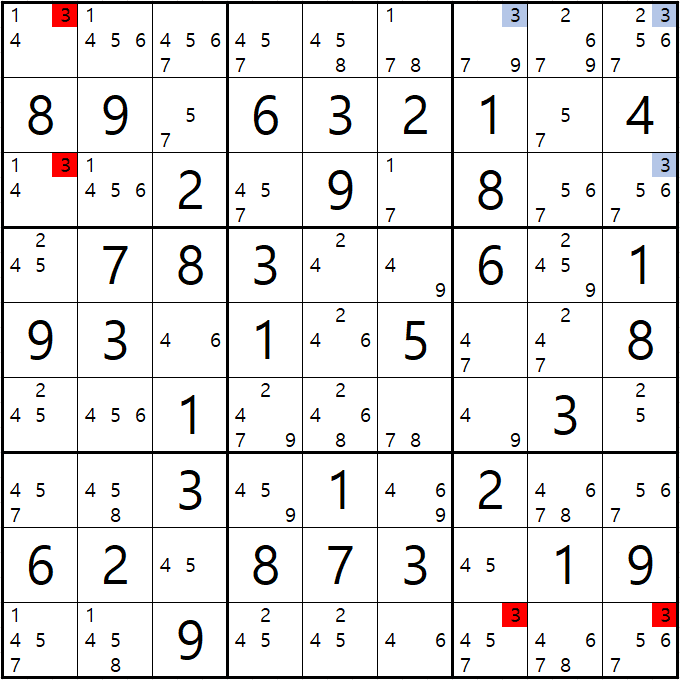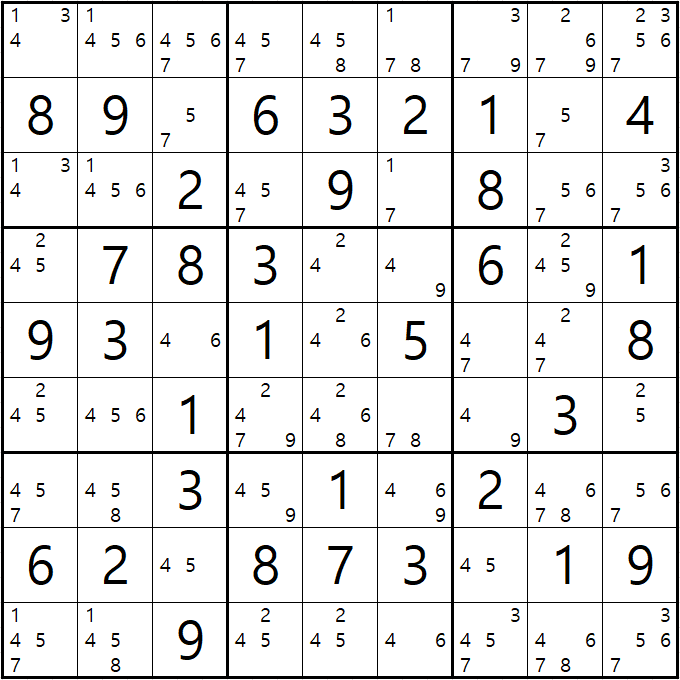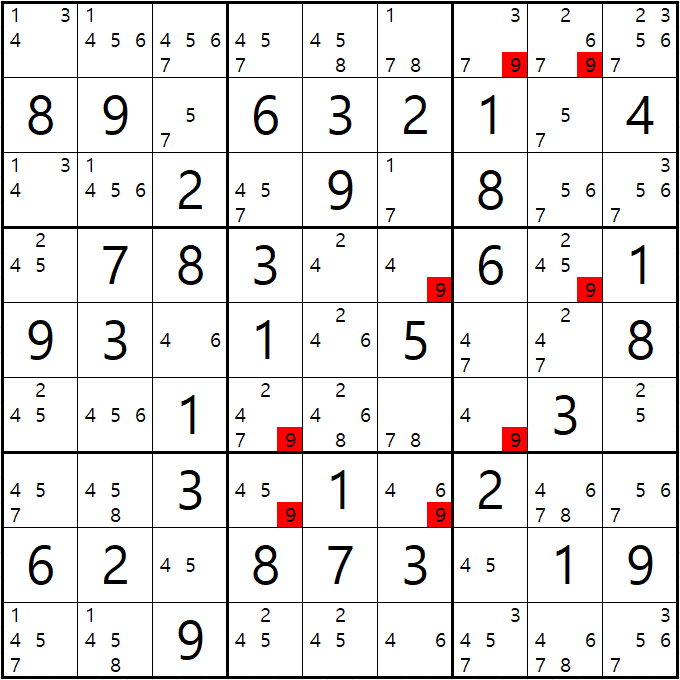
가. 루프형 X사이클의 가장 기본형태로 공식화된 X사이클 루프 체인인 X윙부터 살펴 보자.

빨간 화살표는 스트롱 링크를, 파란색 점선 화살표는 위크 링크를 나타낸다.

만약에 (3,3)이 2가 아니라면 Off > (3,7)칸 On[2] > (7,7)칸 Off > (7,3)칸이 On[2]이 되며

시작점과 끝점이 같은 폐쇄형 순환형 사각형 형태가 완성된다.

On[3]이된 (3,7)칸이 속한 하우스인 3행과 7열에서 후보숫자 2를 제거할 수 있고,

마찬가지로 On[3]이 된 (7,3)칸이 속한 하우스인 7행과 3열에서 후보숫자 2를 제거할 수 있다.

이제는 엑스윙도 체인의 관점으로 바라보면 더 이해가 잘 될 것이다.

그런데 On Off가 바뀌면 결과값도 바뀔 것 같지만 아래의 움짤처럼 바뀌지 않는다. On Off 두 가지 경우의 수 모두 결과값이 같다. 이처럼 루프의 힘은 강하다.

위처럼 후보숫자를 지울 수 있는 증명은 아래와 같이 움짤로 가능하다.

증명 1, (3,3)칸이 2가 아니라면 (=7이라면)

위의 움짤 과 같이

(3,3)이 2가 아니라면 (3,7)이 2가 되고,

(1,7) > 2, (1,8) > 2, (7,7) > 2, 3개의 후보숫자를 지울 수 있다.

(7,3) 이 2가 되면

(9,1) > 2, (4,3) >2, (6,3) > 2, 3개의 후보숫자를 제거할 수 있다.

증명 2, (3,3)칸이 2라면

(3,3)이 2라면

(2,1) > 2, (2,2) > 2, (3,7) > 2, (4,3) > 2, (6,3) > 2, (7,3) > 2, 6개의 후보숫자를 지울 수 있다.

(7,7) 이 2가 되면

(1,7) > 2, (9,9) >2, 2개의 후보숫자를 제거할 수 있다.

즉, 위의 2가지 증명의 결과에서 교집합 되는 (4,3) / (6,3) / (1,7) 은 어떤 경우라도 무조건 지울 수 있다. 로 쓰면 ~

알고 있다. 머리에 잘 들어오지 않는 것을~ 위의 경우의 수 2가지의 결과를 빠른 속도의 움짤로 엮어봤다.

보다 보면 확정 숫자 2가 어디에 있더라도 X윙끼리 연결 시킨 모든 하우스에서 직선 부분만 변하지 않고 X를 유지 하는 것을 알 수 있다. 이렇게 어떤 경우라도 후보숫자를 제거할 수 있는 상황만 뽑아 낸 것이 X윙 공식이다. 위의 움짤과 같이 머리 아프지 말라고 선택하는 설명 방법이 아래와 같은 그림 한 장이 된다. 좌측 상부에서 시작 하는 규칙에 따라 읽어보면

(3,3)이 2가 아니라면 (3,7), (7,3)이 확정숫자 2가 되고 같은 행열에 속한 후보숫자 2, 세개를 지울 수 있다.(그림의 힘은 위대하다~)

이렇게 일단 X사이클의 기본 형태인 X윙으로 워밍업을 했다. 엑스윙 같은 링크 4점에서부터 > 6점 > 8점으로 확장된다고 보면 되겠다.

이제 본격적인 엑스사이클 루프에 대해 알아 보도록 하자! 이제는 그림만 봐도 이해 할 수 있을 거라 생각하고 최대한 어려워 지는 글을 생략하고 그림으로 루프를 익혀 보겠다.

예제1. 아래 움짤은 2x2x2 소드 피쉬가 변형된 것 처럼 보인다. 즉, 2x2x2 젤리 피쉬 또한 X 사이클의 한 종류인데 정형화 시킨 공식으로 보면 되겠다.

(2,7)이 3이 아니라면 (1,9)가 3이 되는 루프가 형성 되는데, 루프를 형성하는 각 칸을 직선으로 이은 행과, 열에 있는 후보 숫자 3을 모두 지울 수 있다. (예제에는 나오지 않지만 동일한 셀에 링크가 연결되어 있다면 동일한 셀의 후보숫자도 지울 수 있다. 위의 움짤에서는 셀 3에 있는 (1,7), (2,7), (3,7)칸과 셀6에 있는 (5,7), (6,7)칸에 후보 숫자 3이 있다면 지울 수 있다.)

단 주의 할 점은 스트롱 링크 > 위크 링크 > 스트롱 링크 > 위크 링크로 시작점과 끝점은 반드시 충돌 되는 링크가 아니어야 한다. 즉, 링크 되는 칸의 갯수는 4개 이상의 짝수로 이루어 진다.

또한 100% 확실한 루프를 찾는 방법은 심플 컬러링 처럼 한칸에 X를 포함한 숫자가 1개만 있는 XY, XZ 형태로 존재하는 칸을 짝수 갯수로 체인으로 연결하는 것이다.

위의 움짤의 결과만 그림으로 변환 시키면 아래와 같다.

잘 이해 했겠지만 한 가지 주의 사항은 스타트는 후보숫자가 2개인 칸에서 하자. 물론 2개를 초과하는 곳에서 출발해도 좋지만, 쉽게 눈에 띄지 않는다. 즉, 후보숫자가 2개인 칸이 많은 곳을 공략하는 것도 한 방법이다.

또한 엑스 사이클 루프 공식 형태가 자주 나오지는 않는다(아니면 내가 아직 잘 못 볼수도 있다.) 루프는 처음 시작시 기븐 숫자가 1,2개인 초반에 찾기 어려운 숫자에 적용하거나 종반에 확실한 페어 및 트리플 지옥에 직면해서 막혔을 때 높은 확률로 좋은 성과를 볼 수 있다.

예제 2.

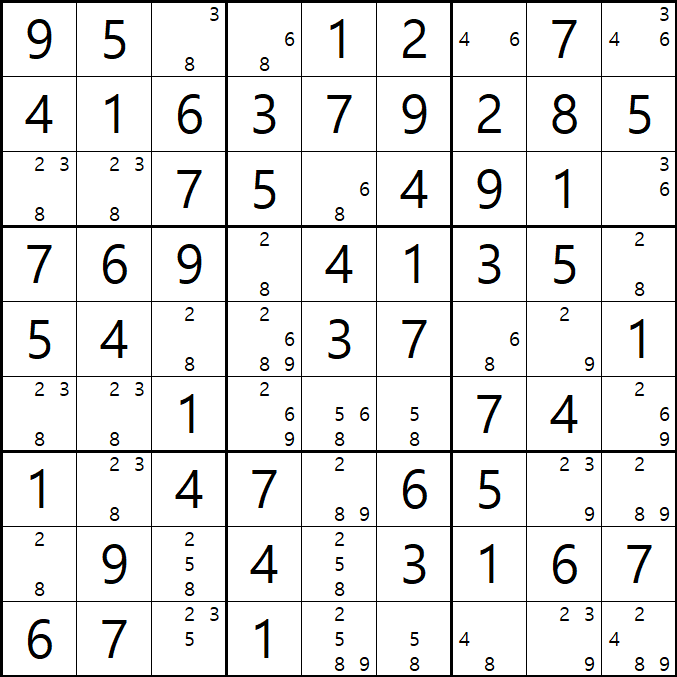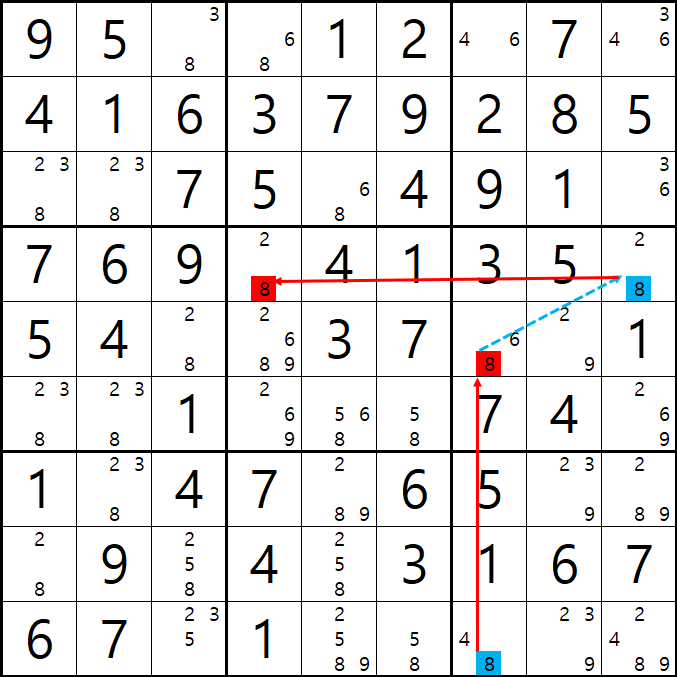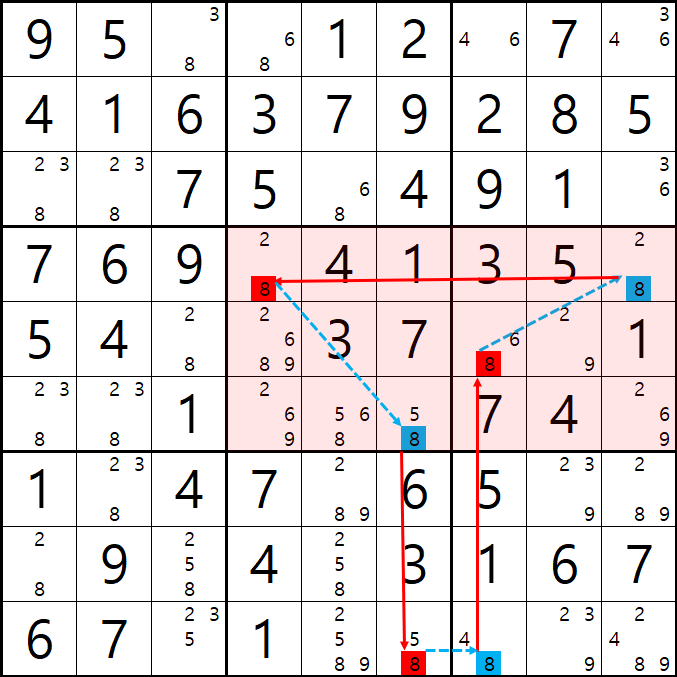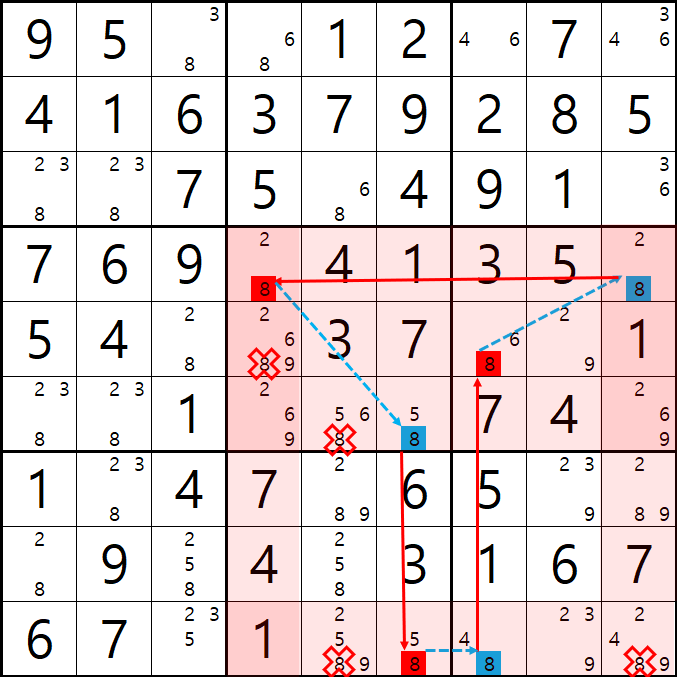
이번 예제는 예제1과는 좀 다르게 셀5, 셀 6에 링크가 한 하우스인 셀안에 있기 때문에 셀6에 있는 후보 숫자 2개와 (9,6)과 (9,7)을 일직성으로 연결한 9행에 있는 후보숫자 8 2개를 지웠다.

아래는 위 움짤의 결과만 캡쳐한 그림이다. 찬찬히 보면서 이해해해 보자.

예제 3.

X체인과 같이 위크 링크를 사용하기 때문에 위의 움짤 처럼 교차도 가능한 것이 루프 체인의 특징이다.

(9,7)이 8이 아니라면(8,0)가 8이 되는 루프가 완성 되어 3행의 8 두개, 셀7의 8 한개, 셀9의 8 1개를 제거하였다.

아래는 위 움짤의 결과만 나타낸 것이다.

이렇게 X 사이클 중에서 루프형에 대해 알아 봤다. 이런 것은 예제를 많이 봐야 하는데, 사례를 찾기가 힘들다. 스도쿠 솔브 같은 사이트에 숫자를 넣고 전후좌우로 돌려 보면서 익히면 좋을 거 같다.

체이닝 기술은 원리가 어렵다가 보다는 찾기가 어렵다. 판마다 메모장을 열어서 그림을 그리기 어렵기 때문인데, 종반에 확실한 페어, 트리플이 나올 때마다 시간이 좀 더 걸려도 검토해보자. 어느 순간부터 패턴이 딱 보이게 될 것이다.

또한 초반에는 싱글 체인(=심플 컬러링) 처럼 모든 링크가 후보숫자가 2개만 있는 스트롱 링크를 위주로 찾는 것이 좋겠다.

추가사항...

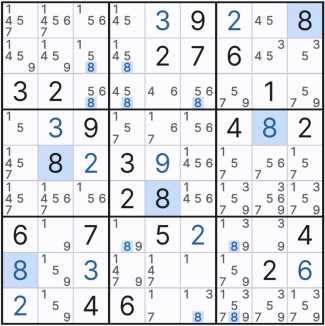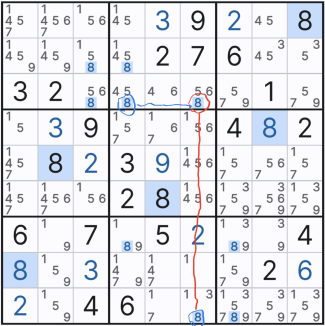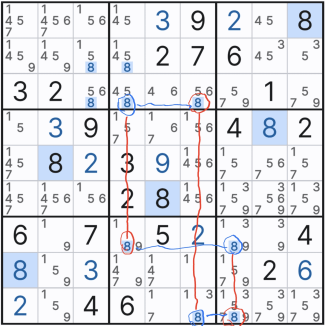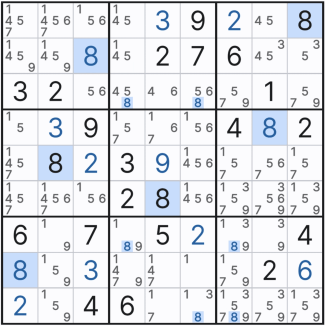
이제 나도 조금씩 보이기 시작한다. 다른 체인 기술과는 다르게 루프형태는 매우 명확해서 좀 더 잘 보이는 것 같다.

또한 아래와 같이 11칸짜리 젤리 피쉬를 찾아야하는 상황에서도 행에 4칸, 열에 4칸 이렇게 세지 않고 아래와 같이 X 사이클 루프형을 쓰면 젤리 피쉬보다 더 명확하고(나는 젤리 피쉬 찾기가 쉽지 않다.)

젤리피쉬 1개보다 좀더 많은 3개의 후보수를 지워나갈 수 있다.

동일한 후보숫자가 몰리면 꼭 루프형은 찾아 보도록 노력하자!!

X 사이클 체인의 하위 종류인 위크 링크 형태는 심플 컬러링(Simple Colouring)이라고도 불리는 싱글 체인과 99% 같은 모양인데 한 가지만 다르다. 심플 컬러링은 시작점과 끝점 모두 스트롱 링크로 연결되는데 반해서

나. X사이클 위크링크 형태는 시작점은 스트롱 링크로 시작해서 교대로 위크 링크 > 스트롱 링크 > ... > 위크 링크가 교대로 나타나다가, 끝점은 항상 스트롱 링크로 끝이 나며 시작점과 끝점이 향하는 타겟과의 링크는 둘 다 위크 링크가 된다.

즉, 심플 컬러링은 한정적인 상황에서 쓰이는데 반해서, X 사이클 위크 링크 체이닝은 좀 더 넓은 상황에서 쓰는 링크이다. 어떤 사이트에서는 이를 X Chain이라고도 부르는 것 같다.

다시 정리 하면 X사이클 위크 링크 형태는

1. 시작점과 연결되는 링크는 후보숫자 X끼리 스트롱 링크로 시작하여 위크 링크가 교대로 나타난다.

2. 시작점과 끝점이 같이 바라보는 칸의 후보 숫자 X를 제거 할 수 있다.

3. 어느 칸에서 부터 시작하여도 답은 항상 동일하다.

체인 규칙은 대부분 스트롱 링크 거나, 스트롱 링크와 위크 링크가 반복적으로 나타나지만 한점에 동일한 링크 형태 2개가 몰리지 않는데 X사이클에서는 위크 링크형과 함께 스트롱 링크에서도 동일한 링크가 한점에서 만난다.

그렇기 때문에 해답이 명확하다.

말로 하면 어려우니까 한 게임안에 X 사이클 (위크링크 형태)가 3가지가 나오는 자료를 찾았다 움짤로 보자.

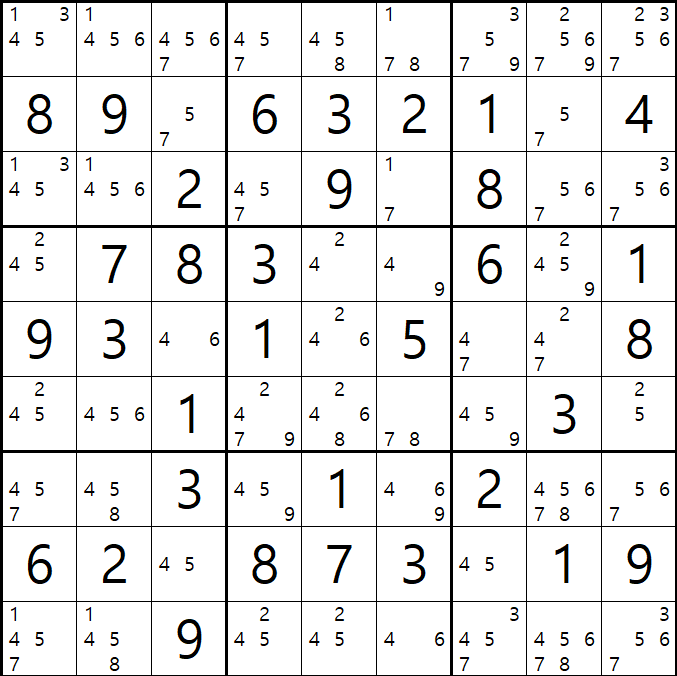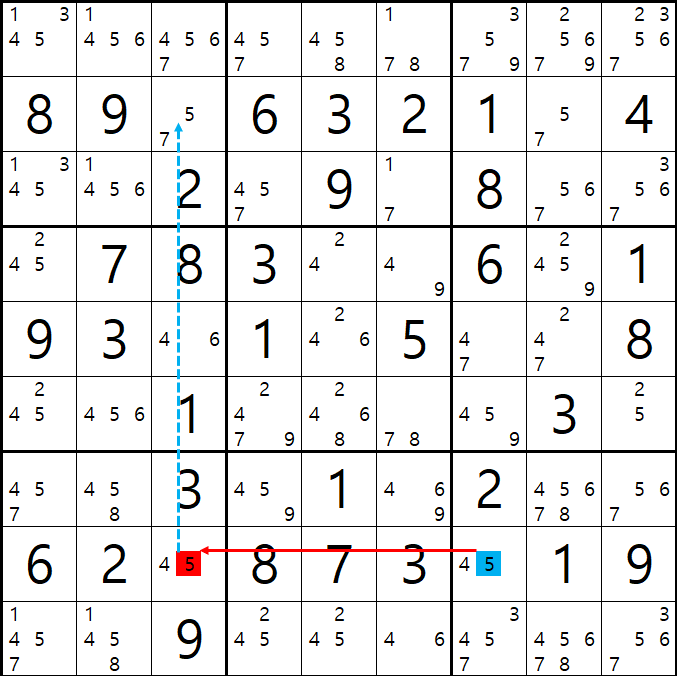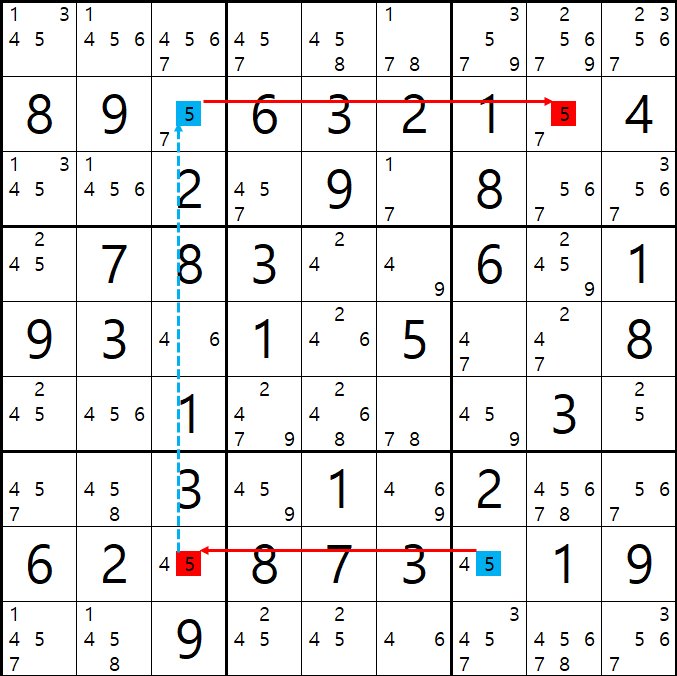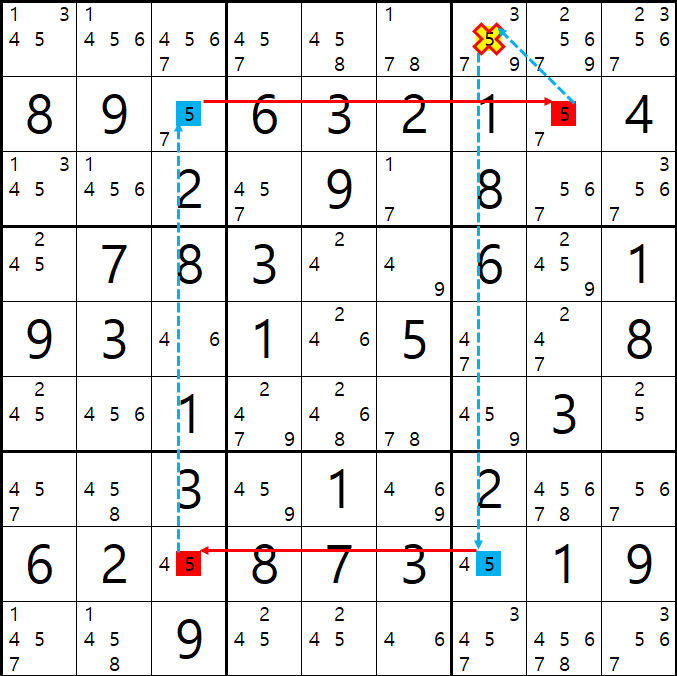
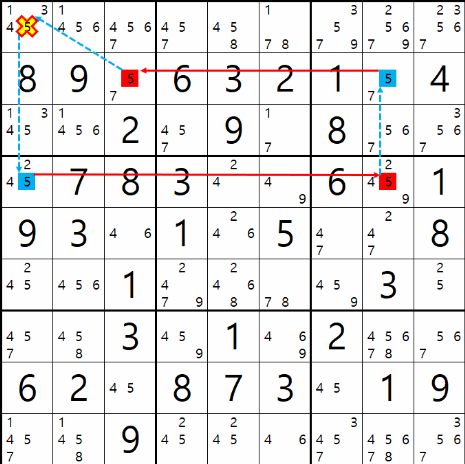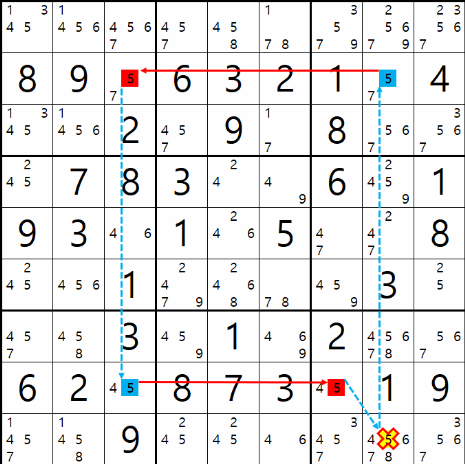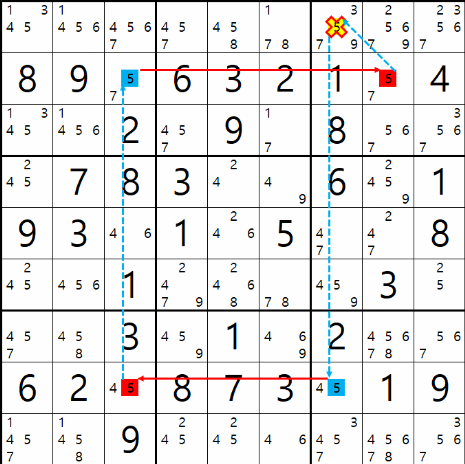
예제 001.

위의 움짤과 같이 시작점 (4,1)칸이 5가 아니라면 끝점 (2,3)칸은 5가 되어 시작점과 끝점이 마주보는 (1,1)칸의 후보수 5를 지울 수 있다. 또한 심플 컬러링은 주로 후보수가 2개인 칸에서 시작 하지만

X사이클 위크 링크형은 시작점과 끝점이 달라도 항상 같은 결과가 나온다.

심지어 제거될 후보숫자에서 출발을 해도 결과는 같다.

홀수 갯수로 닫힌 다각형만 만들 수 있으면 51% 이상의 확률로 X 사이클 체인 공식이 적용된다고 보면 된다.

예제 002.

위의 움짤과 같이 시작점 (2,8)칸이 5가 아니라면 끝점 (8,7)칸은 5가 되어 시작점과 끝점이 마주보는 (9,8)칸의 후보수 5를 지울 수 있다.

예제 003.

위의 움짤과 같이 시작점 (8,7)칸이 5가 아니라면 끝점 (2,8)칸은 5가 되어 시작점과 끝점이 마주보는 (1,7)칸의 후보수 5를 지울 수 있다.

위의 예제 1~3의 결과만 움짤로 엮어봤다.

자. 엑스 사이클 위크 링크형은 심플 컬러링 복습 차원이라서 증명도 하지 않았다.

위의 다이어그램이 잘 이해가 가지 않는다면 이전 글 '싱글 체인'에 관한 글을 읽고 오자!

스도쿠 15. 고급공식/ 싱글 체인(심플 컬러링)-움짤, 패턴

스도쿠 기술이 초급에 머물러 있는 스린이(=스도쿠 어린이)인 나는 계속 비슷한 초급 기술만 쓰니까... 스도쿠가 좀 무료해 지고 있던 찰라였는데 아래와 같은 난제가 찾아 왔다. 셀1-67페어, 48페

inoks.tistory.com

또한 스도쿠 고급공식은 실전에서 잘 나타나지 않는다. 고급공식을 써 먹으려면 메모장을 열고 그림을 그려봐도 아리송해서 못 푸는 경우가 생기고 실제로 나타난다해도 긴가 민가 하다가 시간을 낭비할 때가 많다. 그래서 생각해 낸 것이 많이 봐야 정확히 알 수 있다였다.

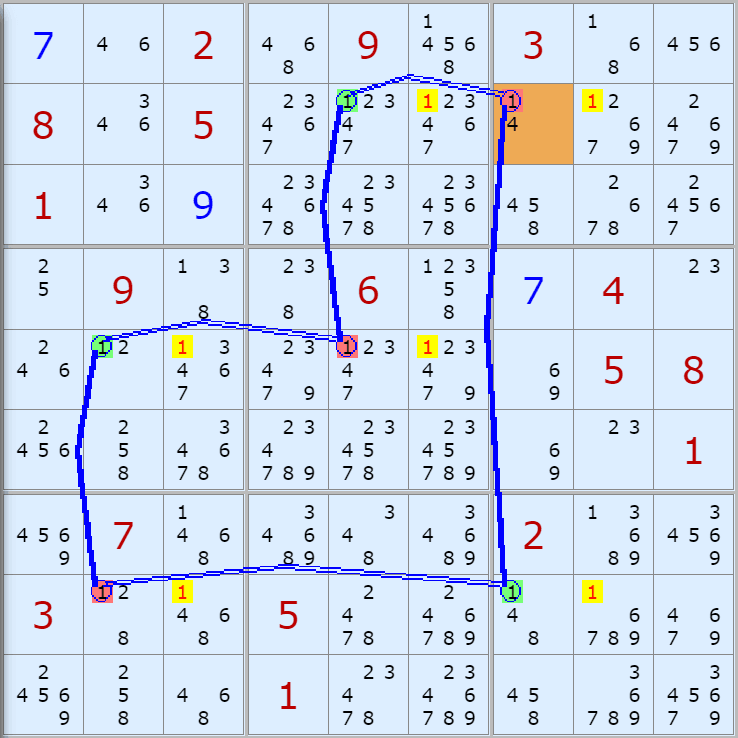
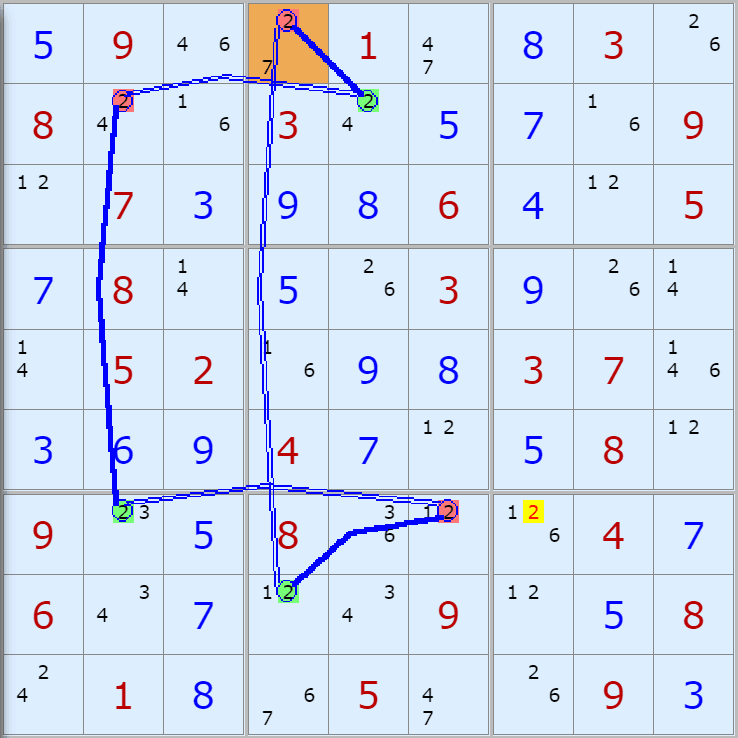
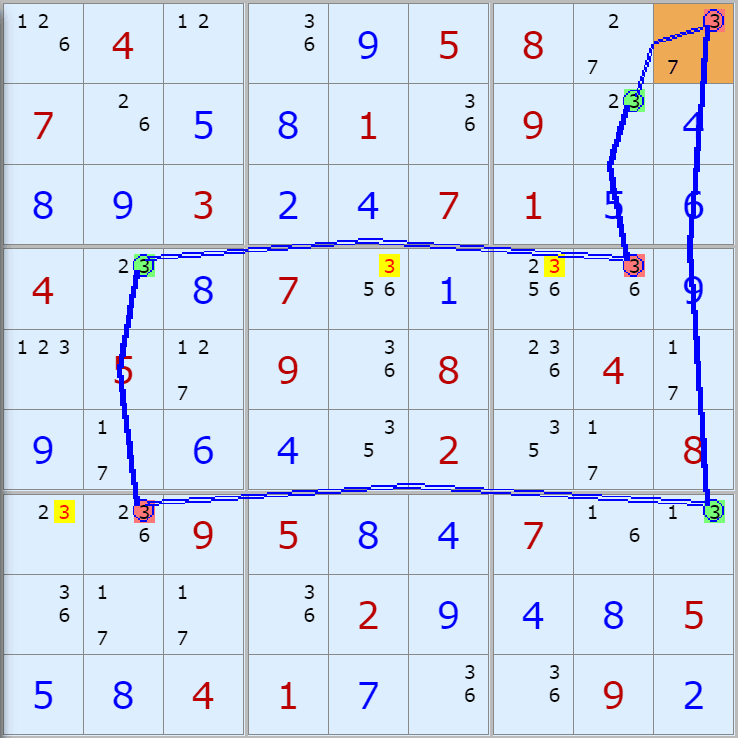
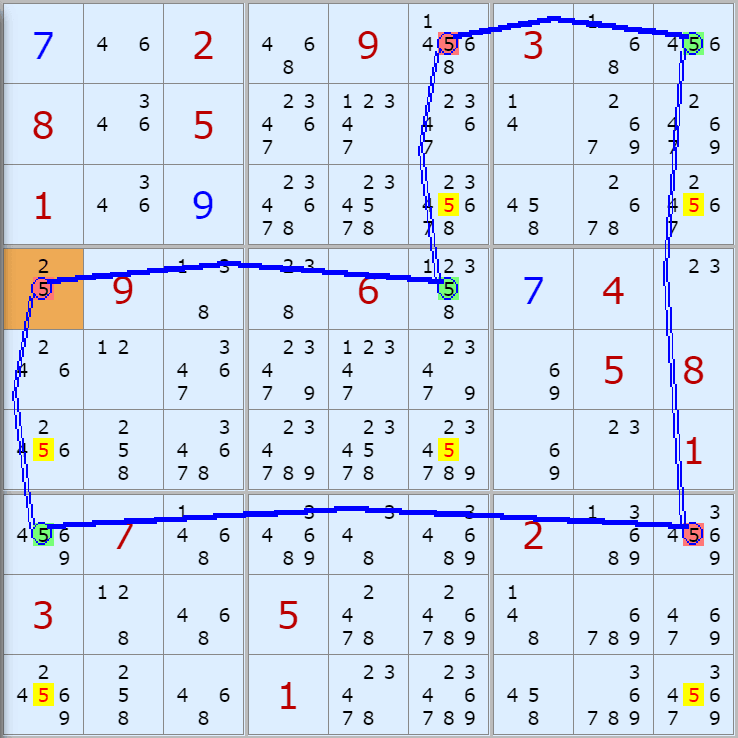
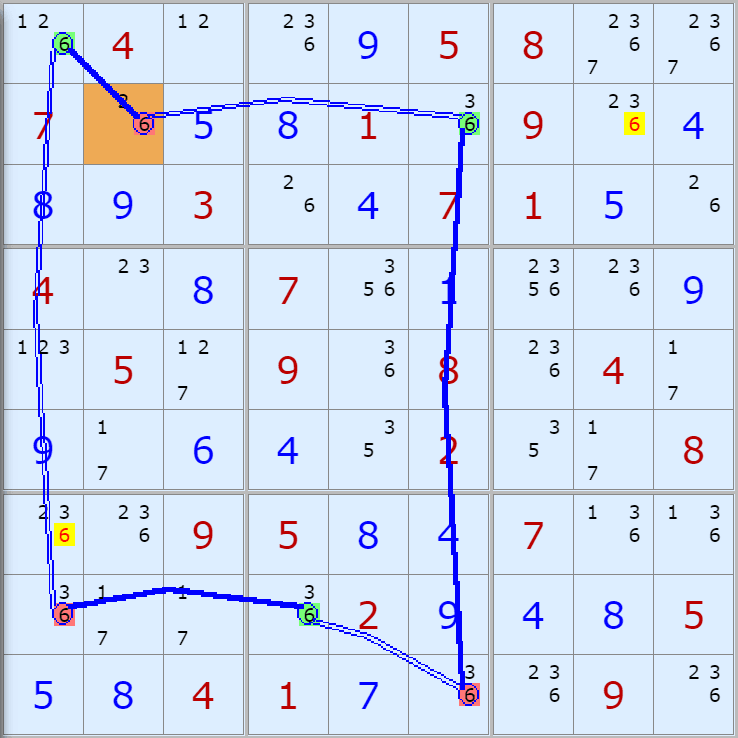
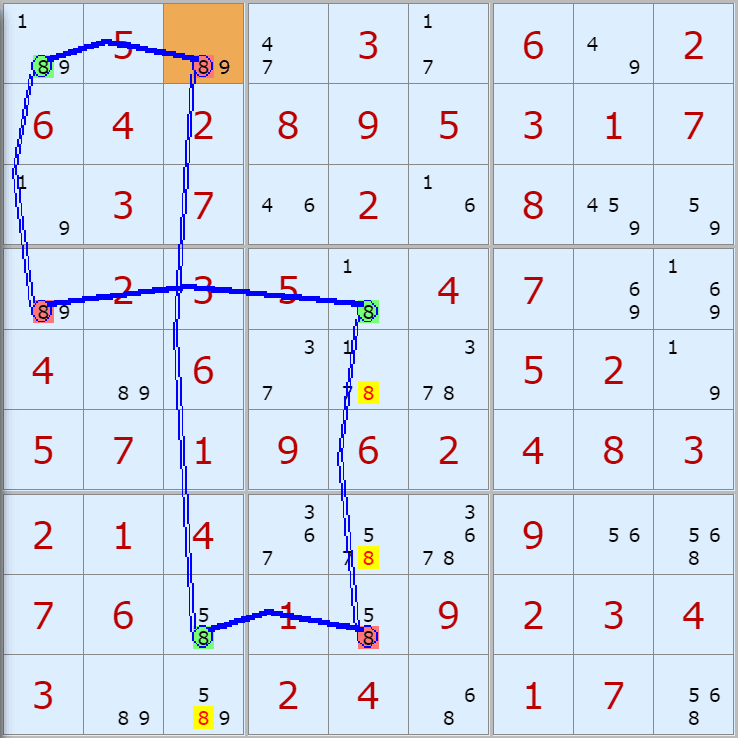
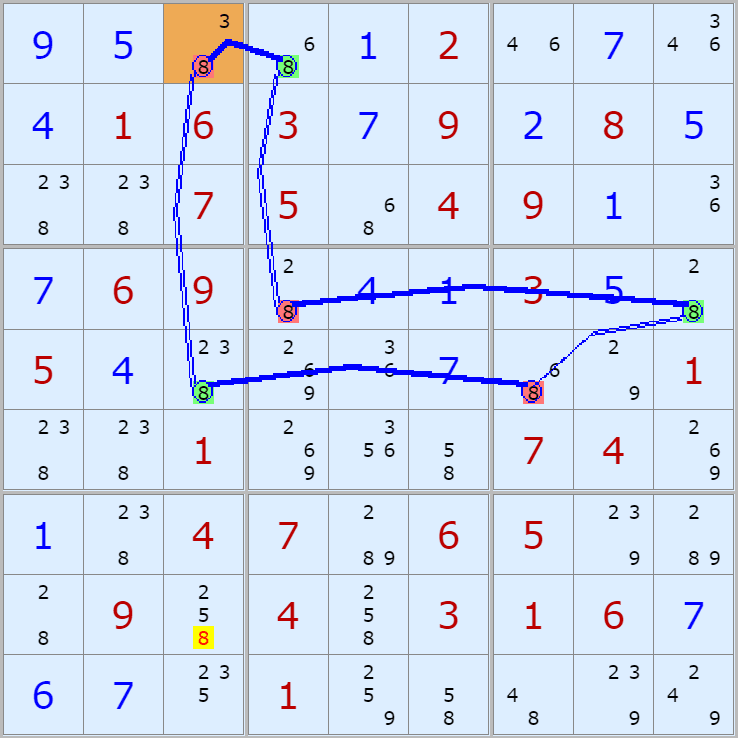
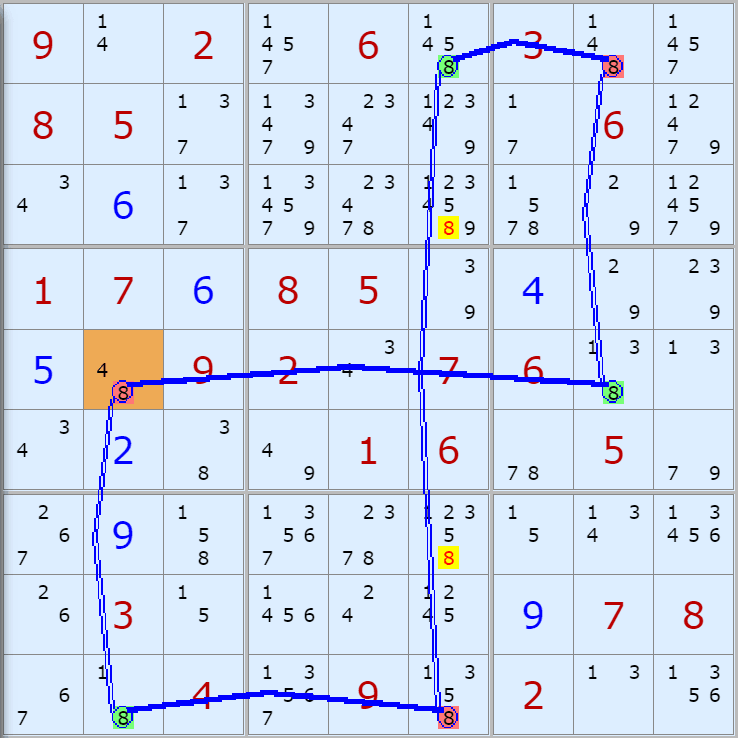
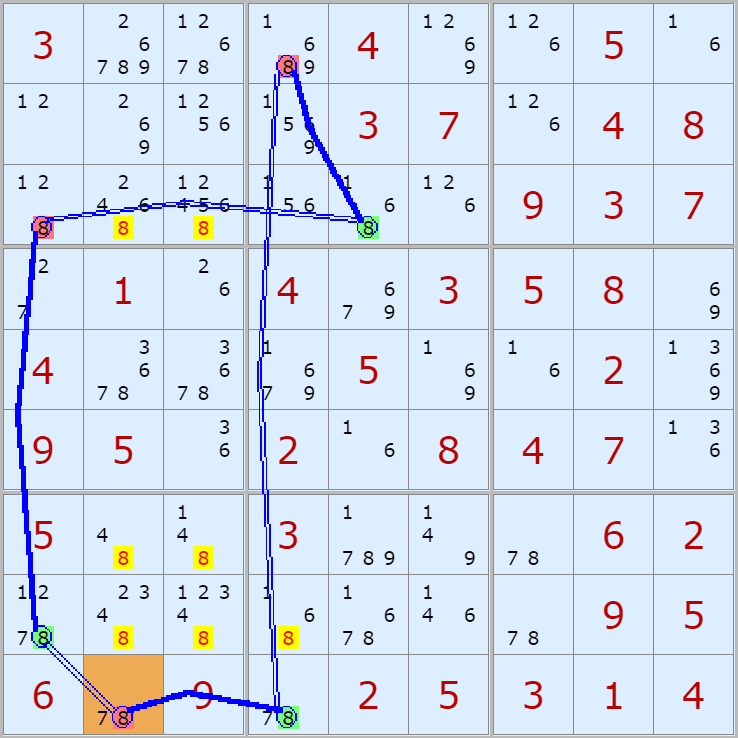
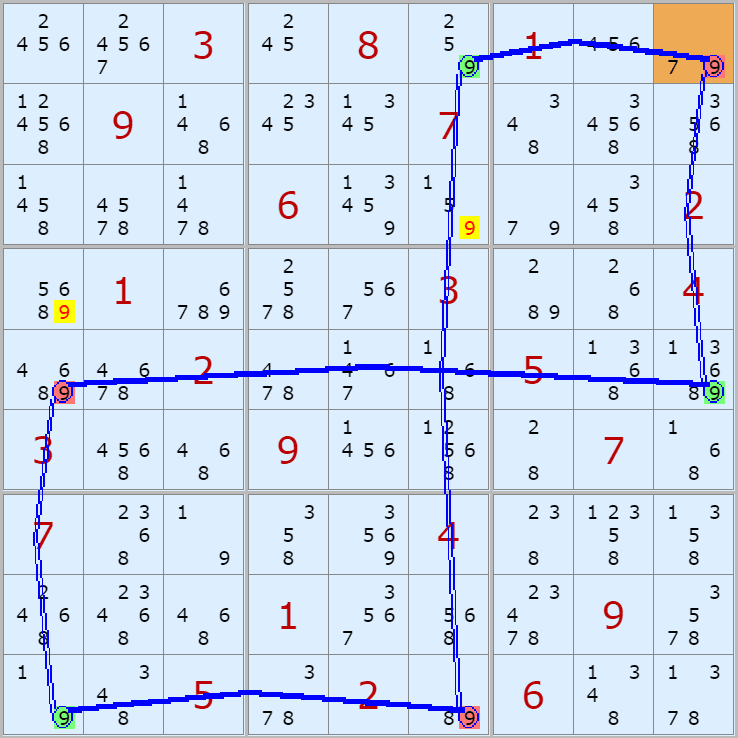
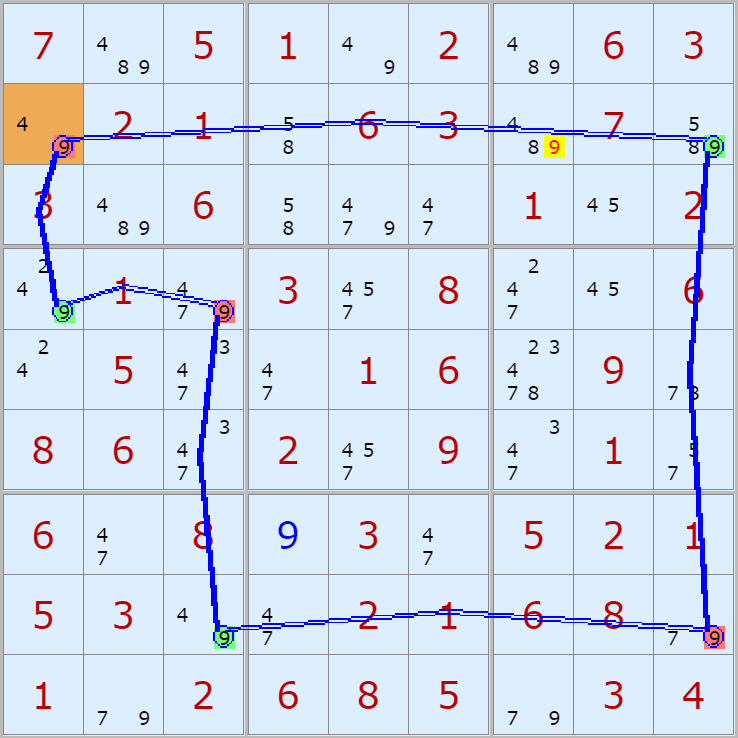
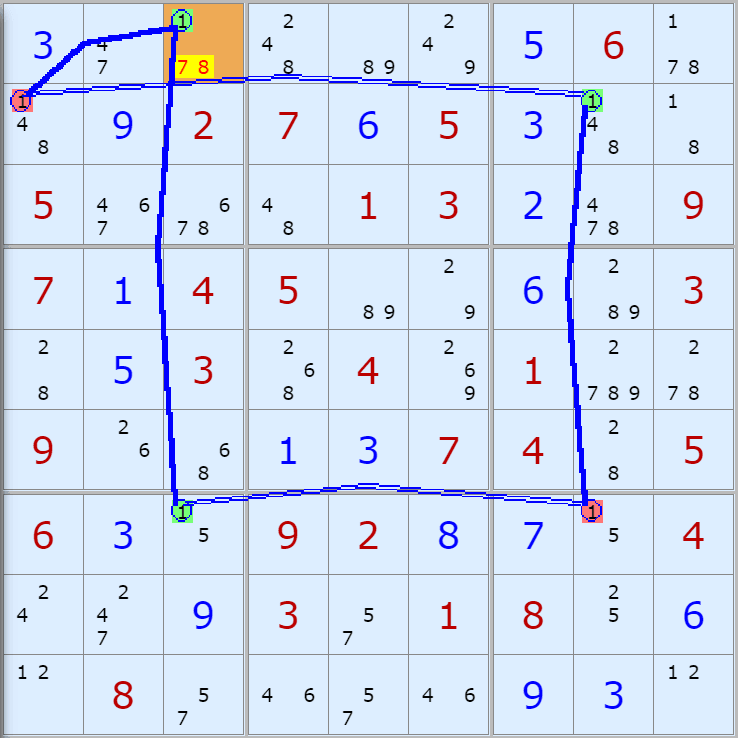
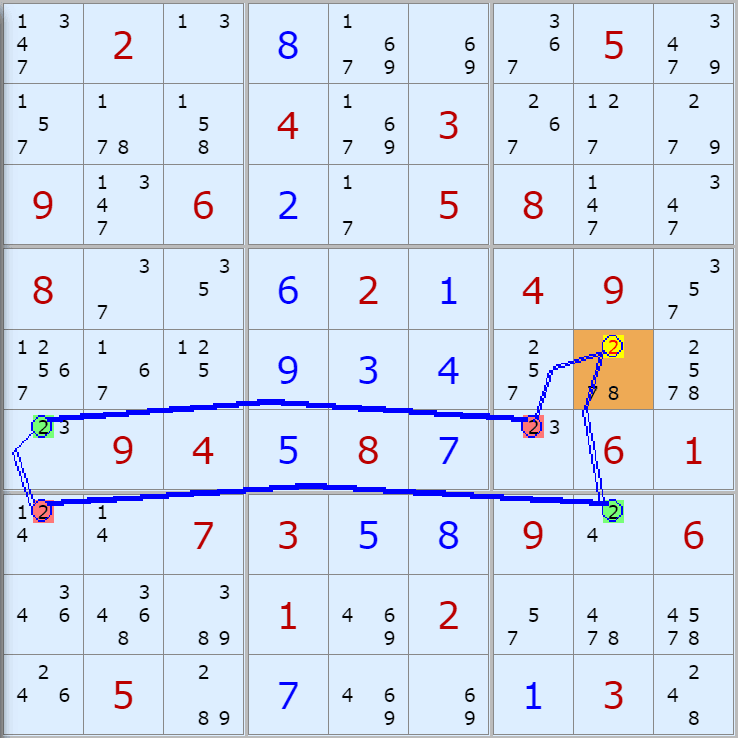
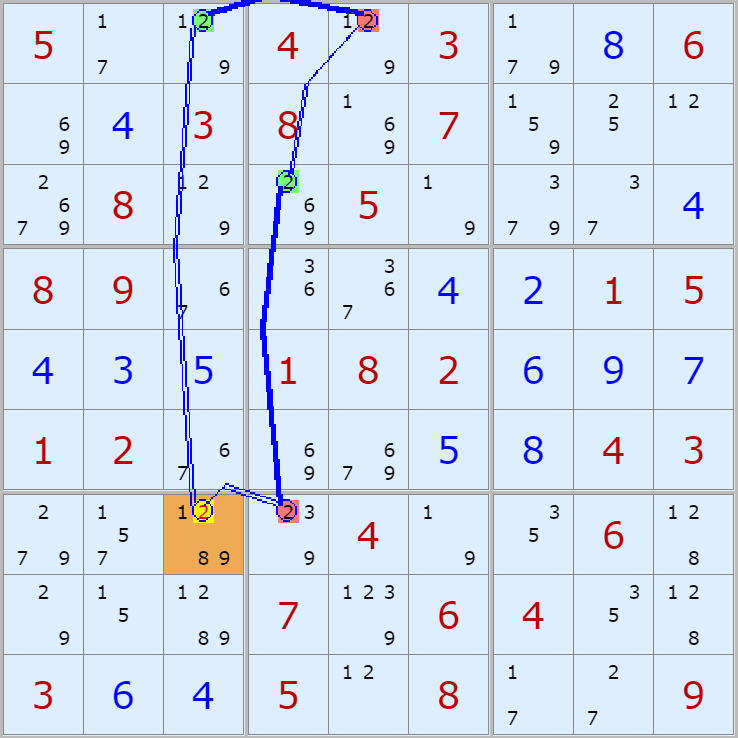
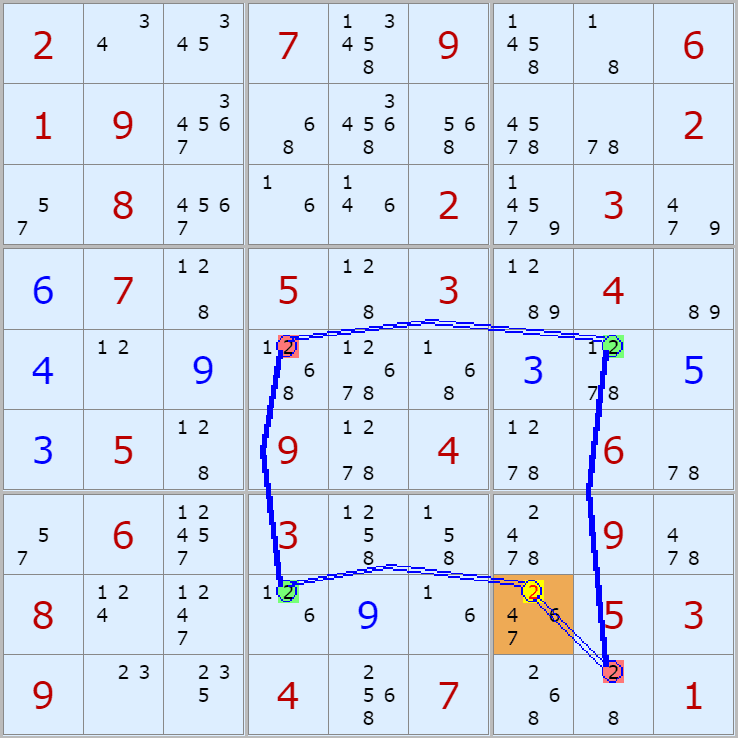
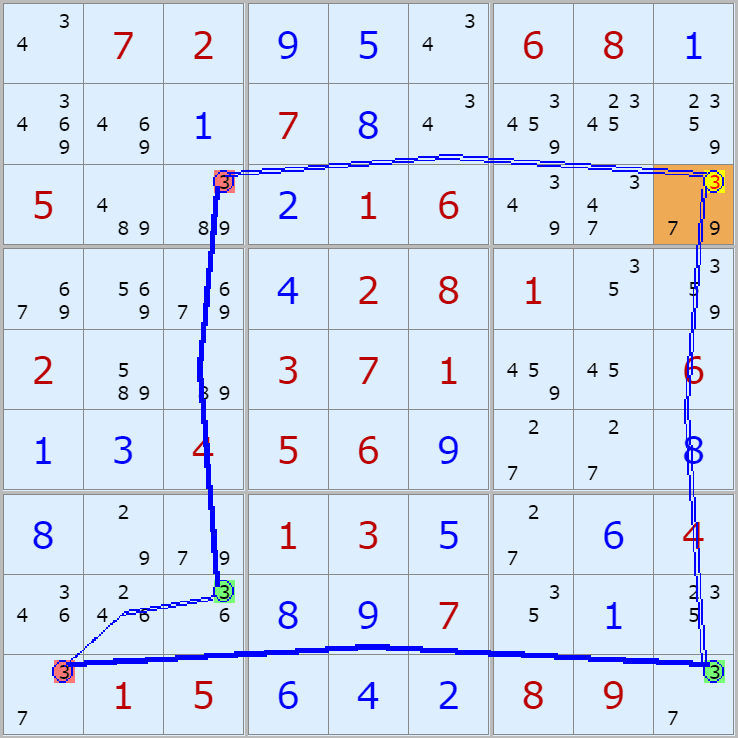
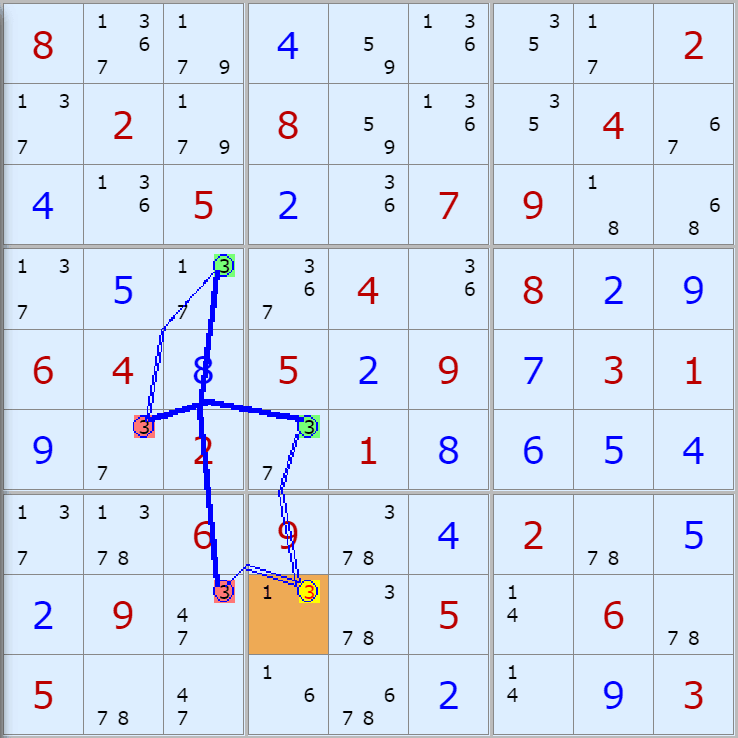
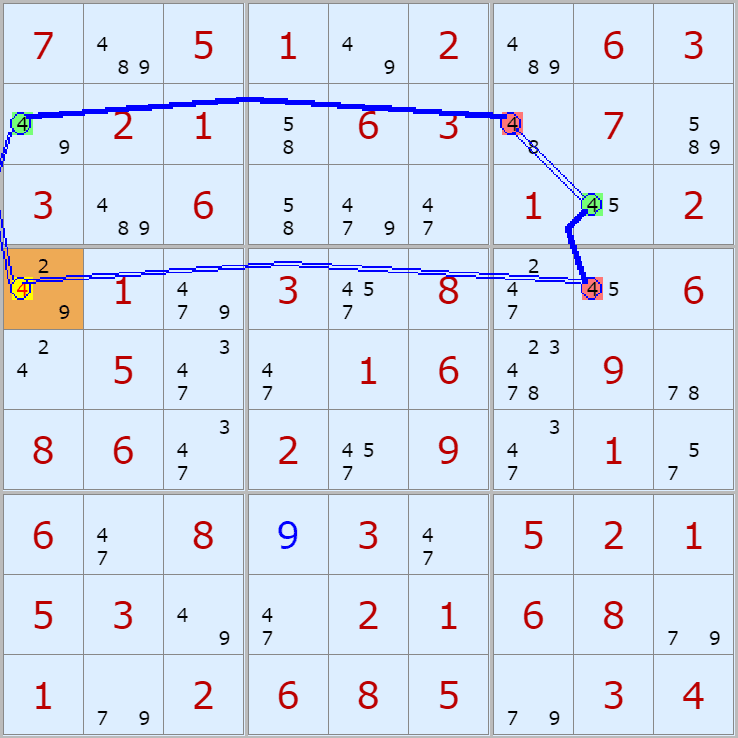
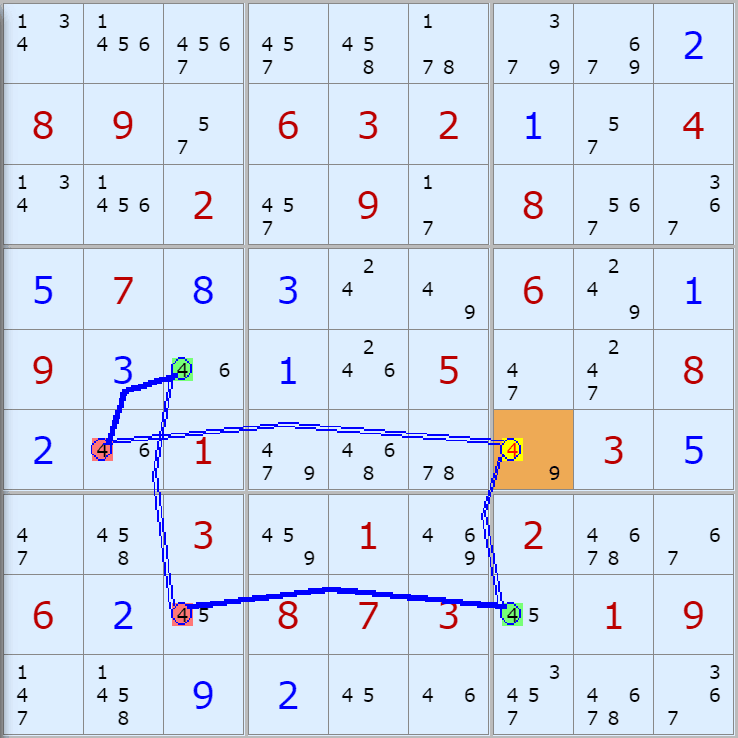
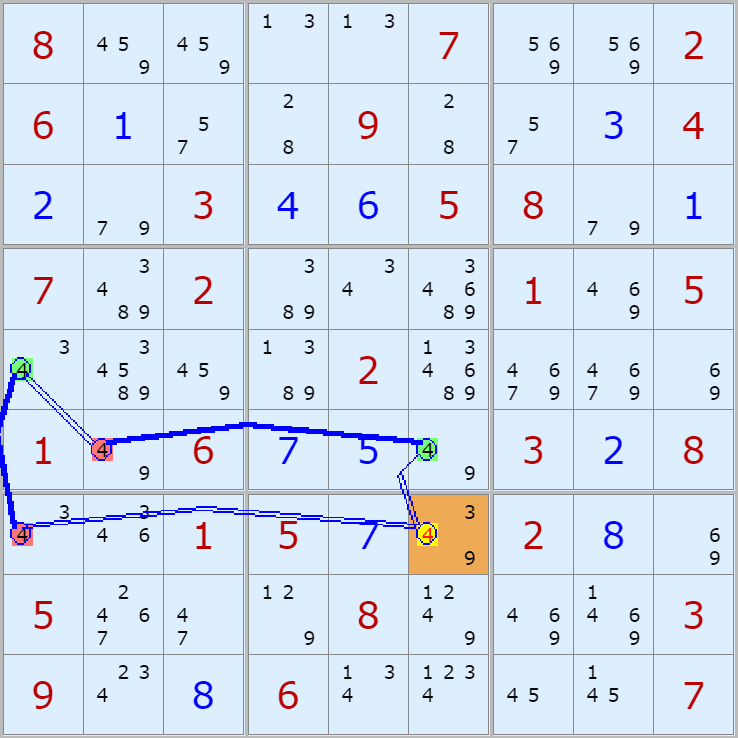
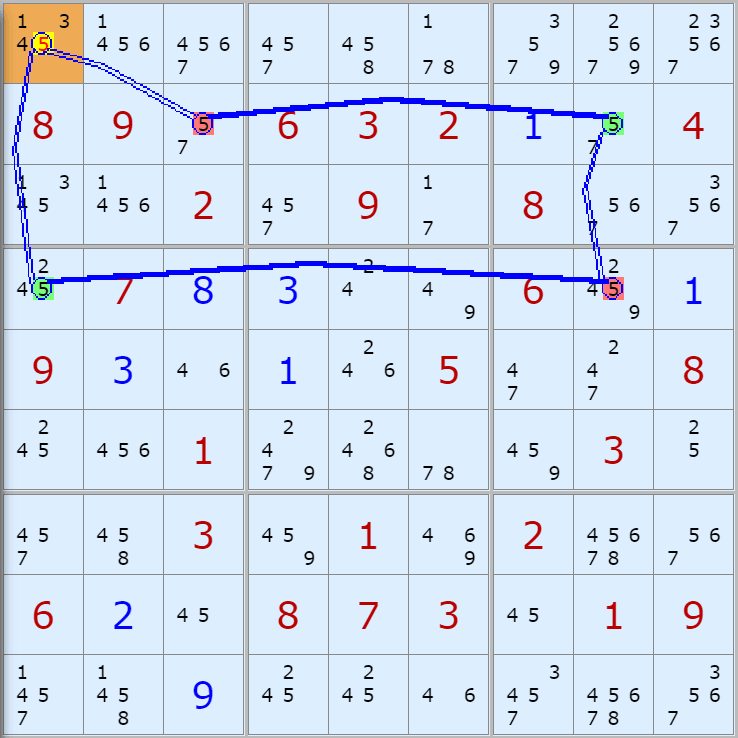
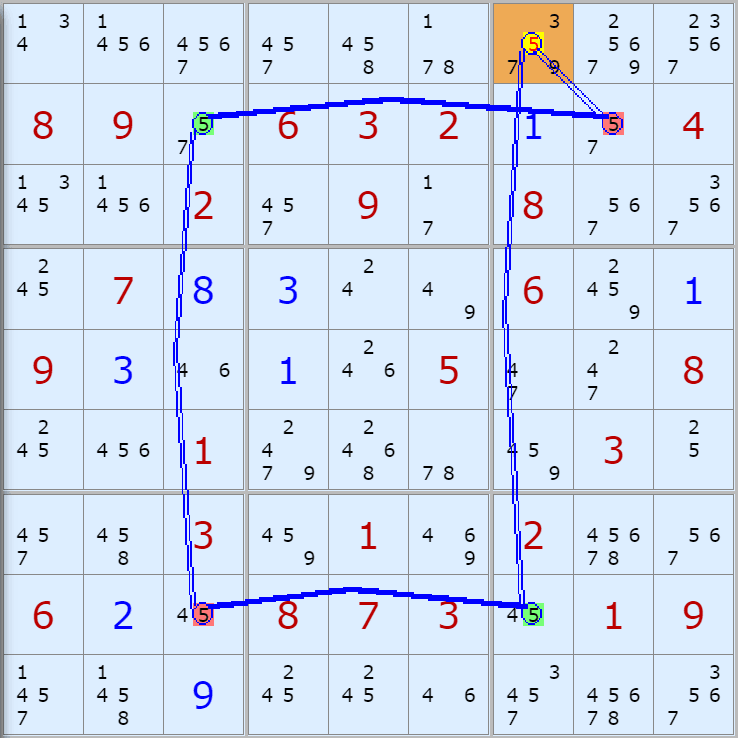
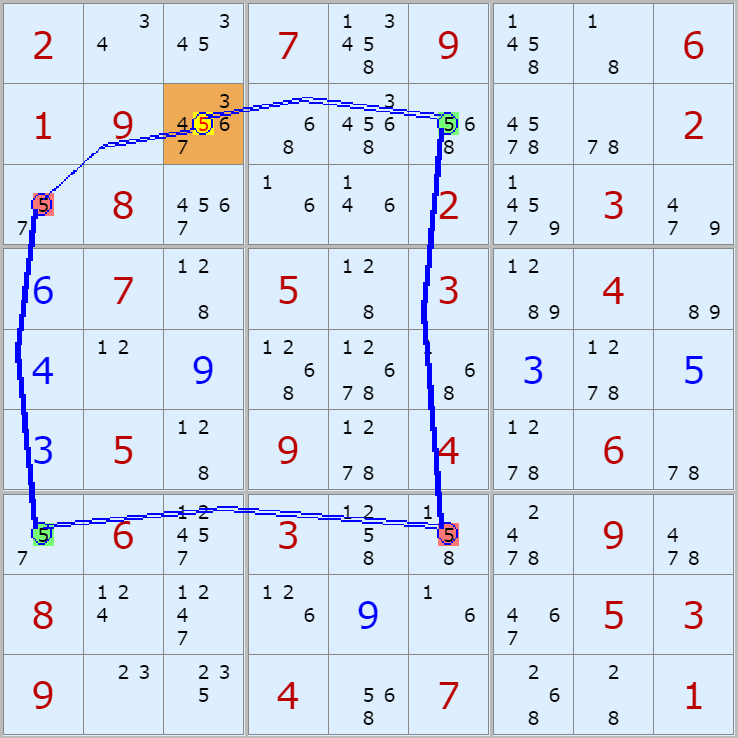
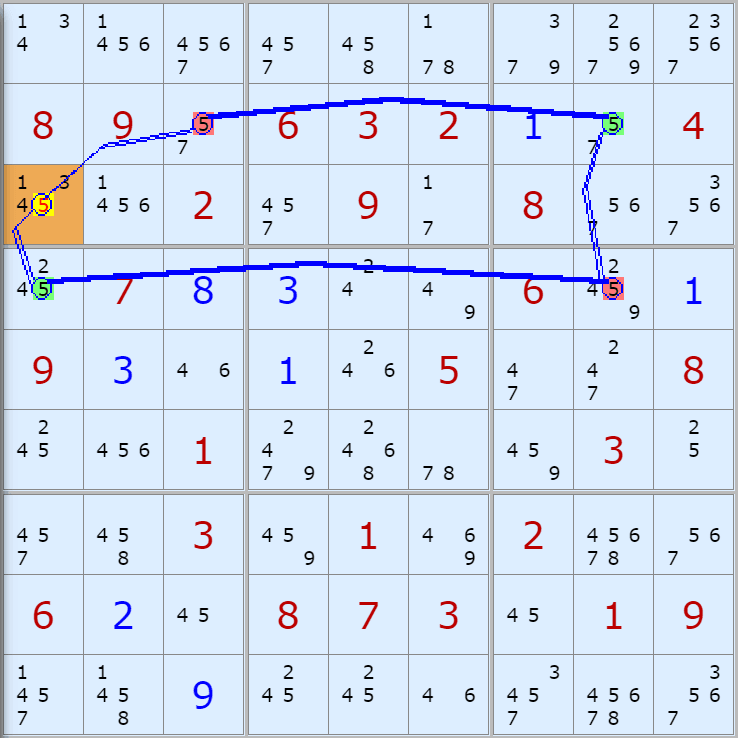
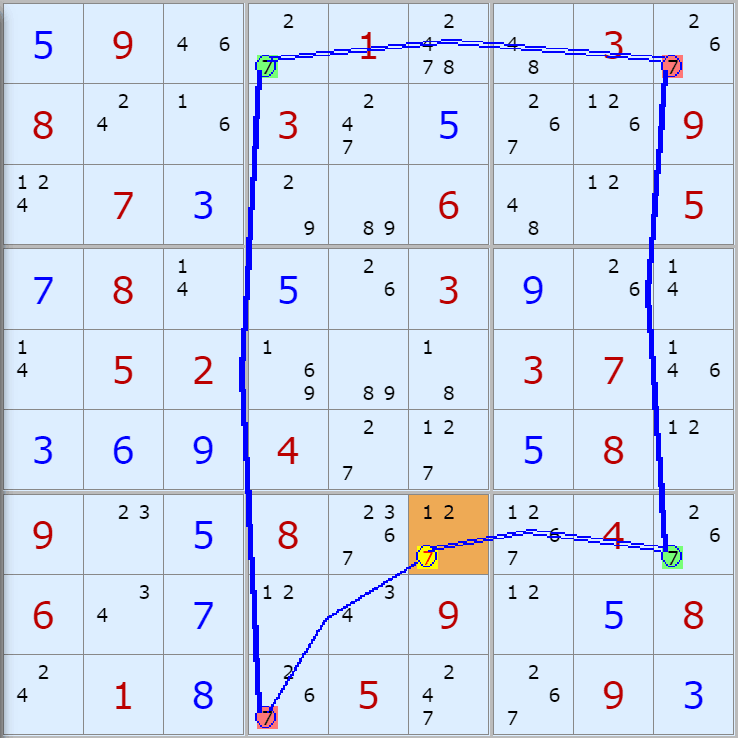
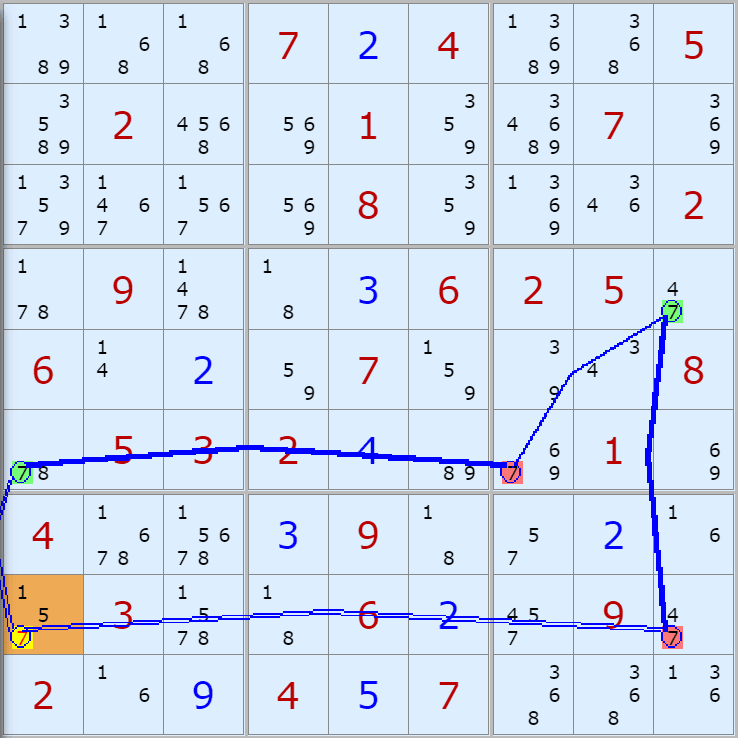
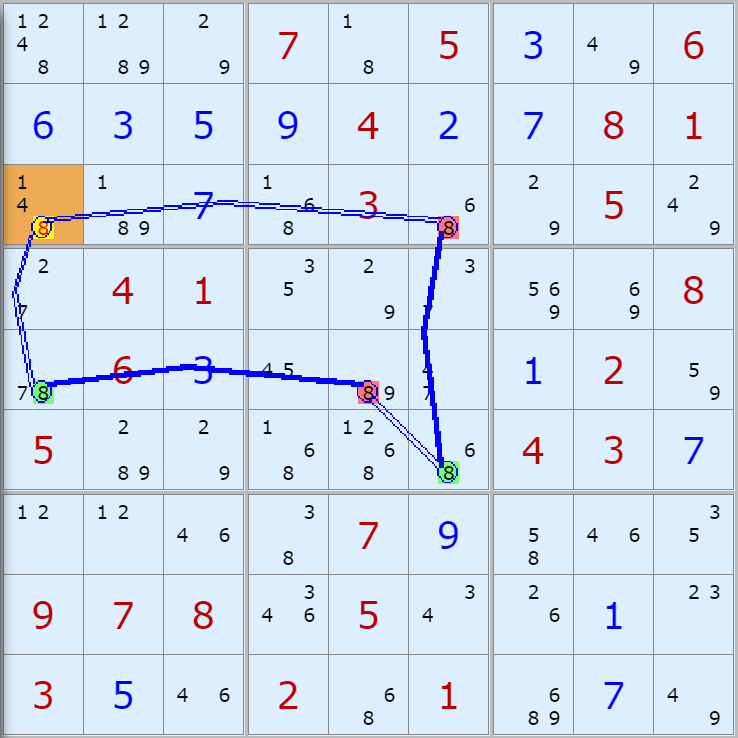
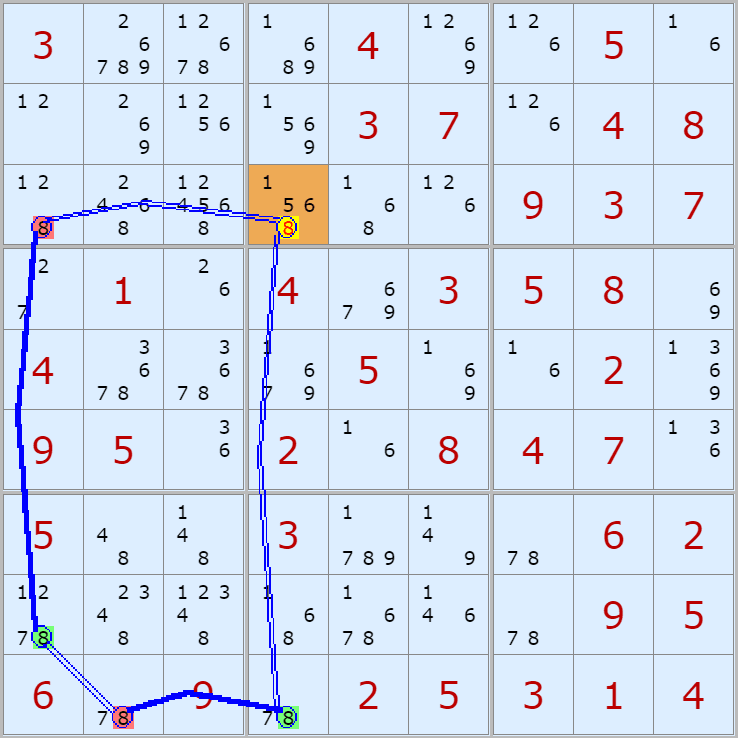
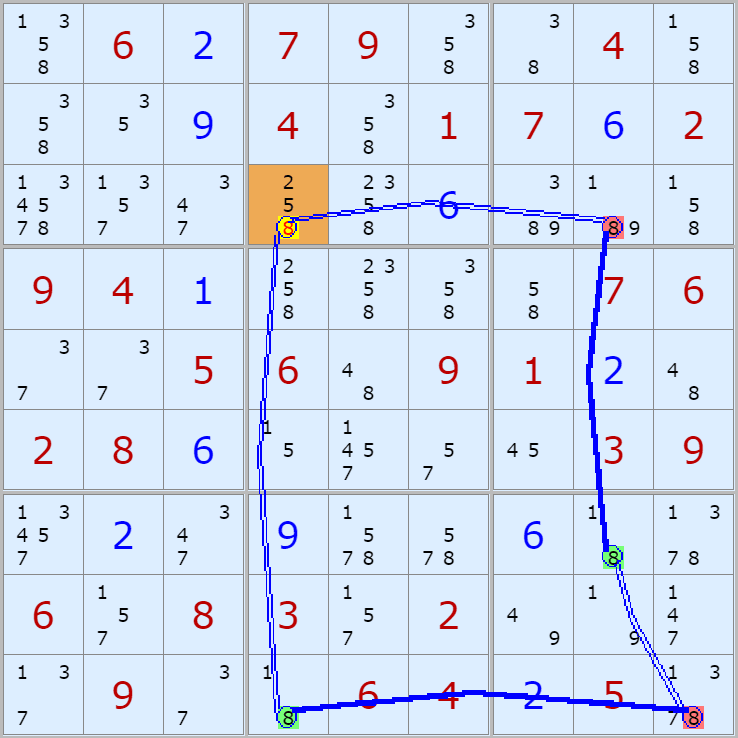
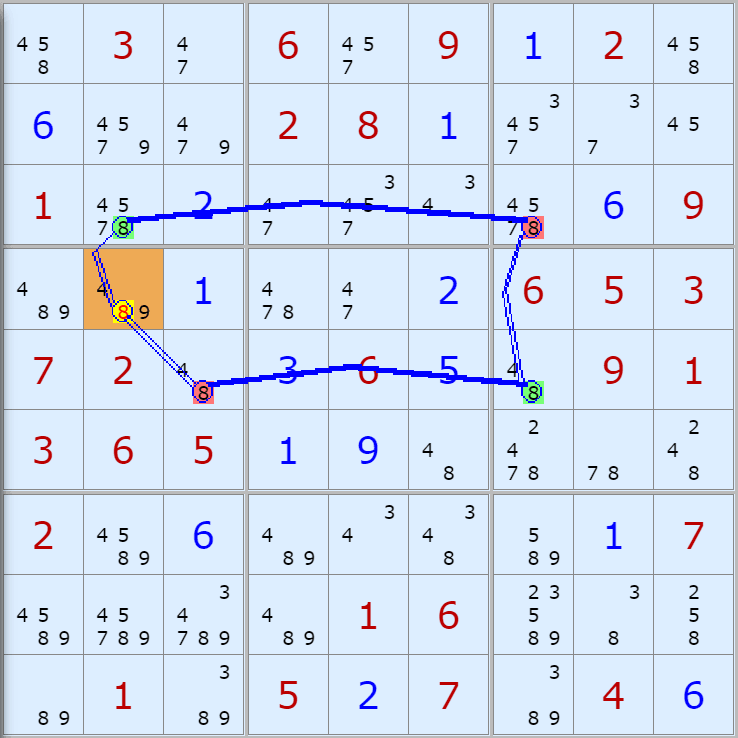
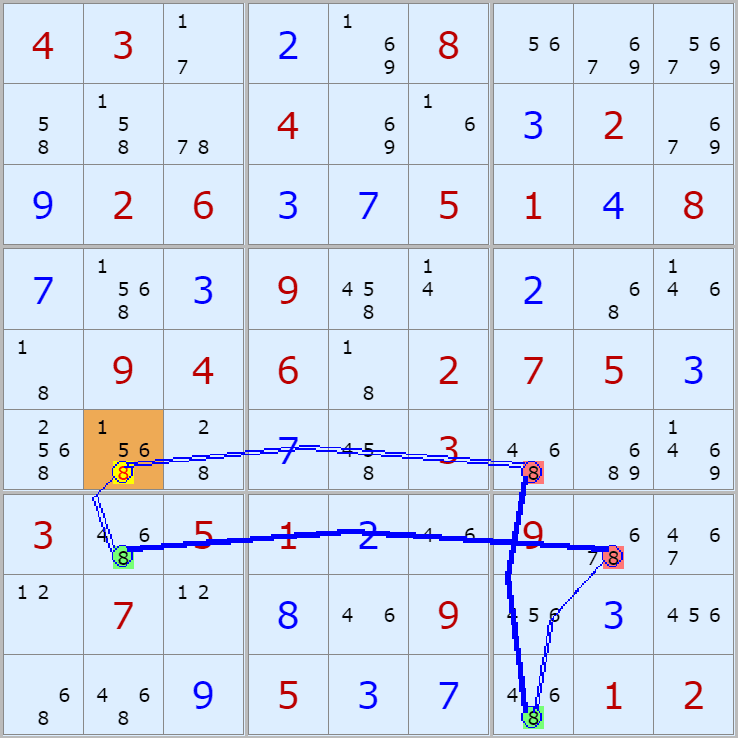
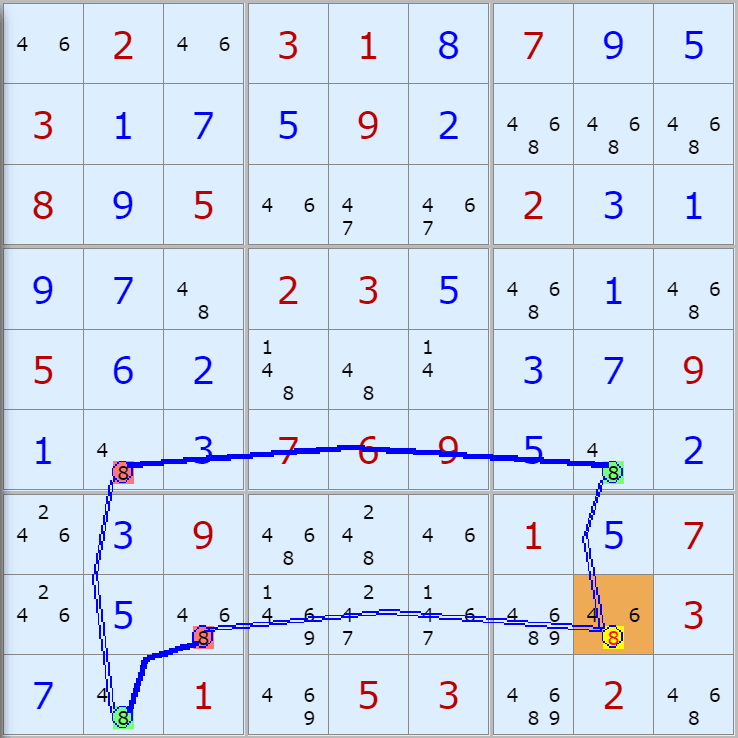
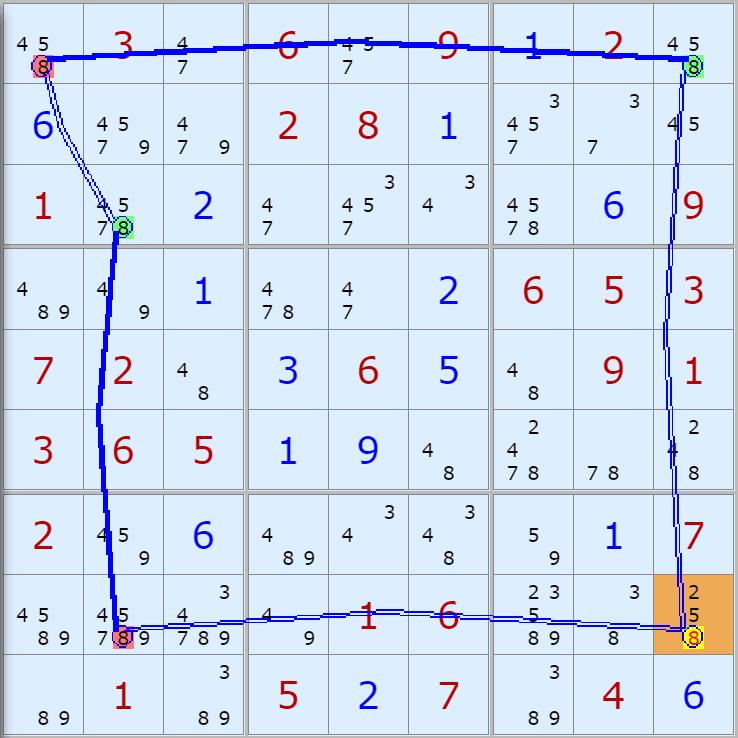
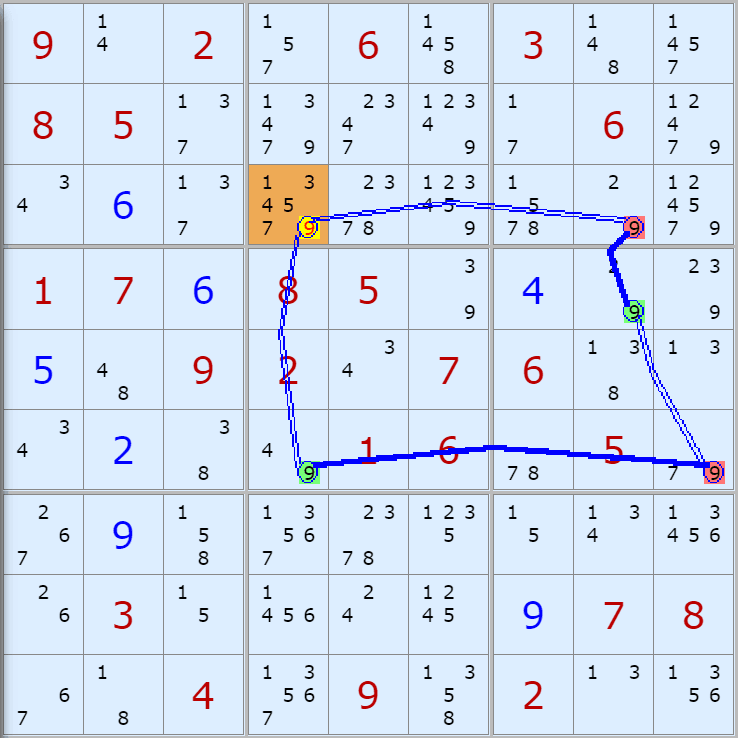
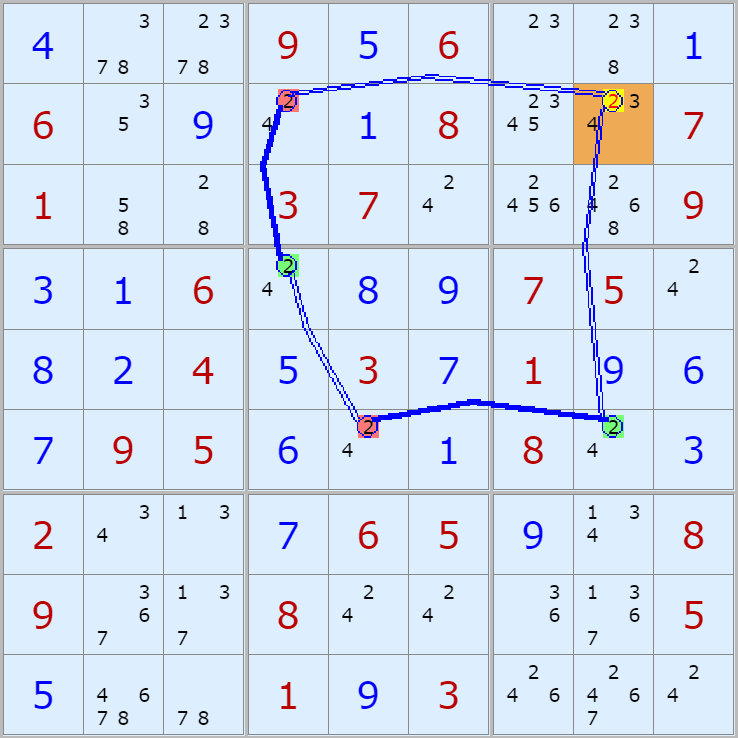
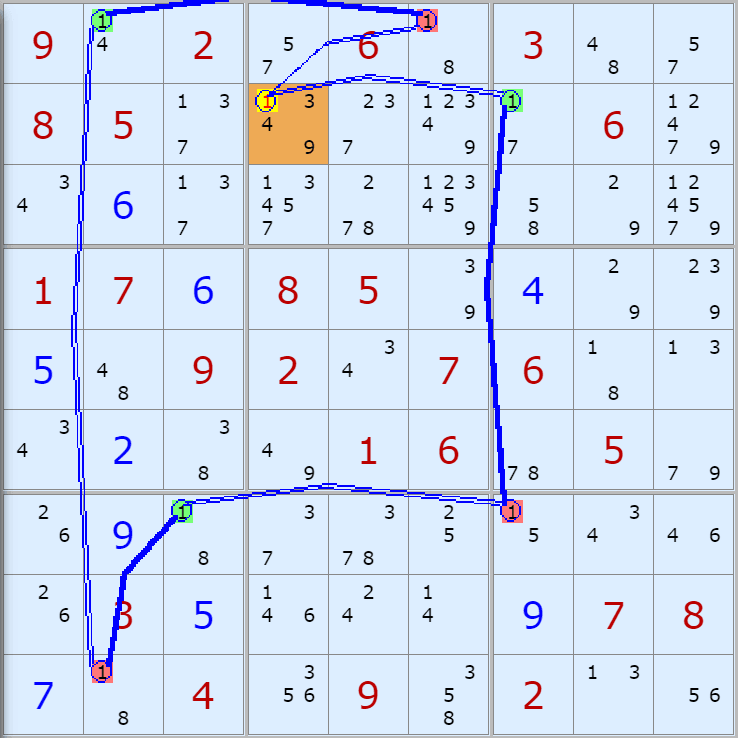
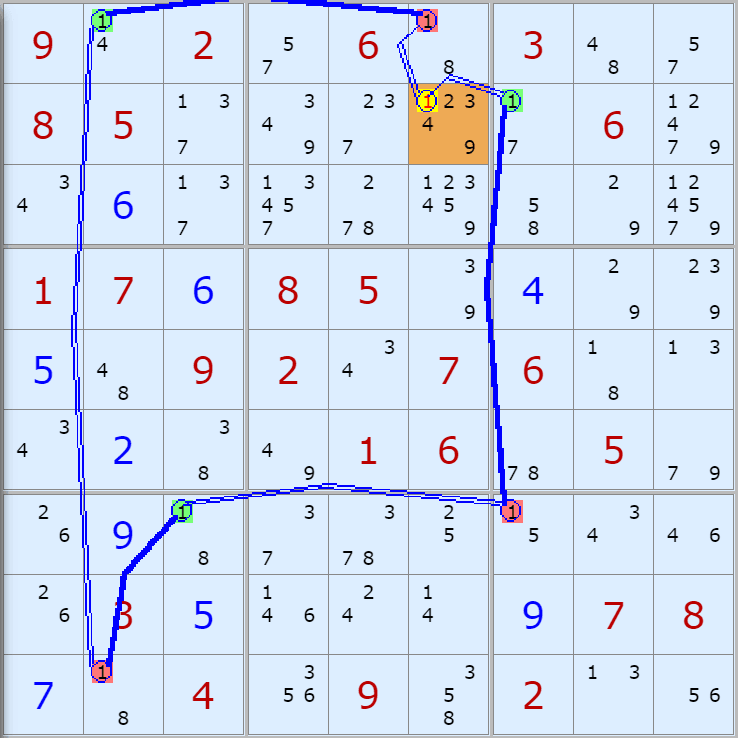
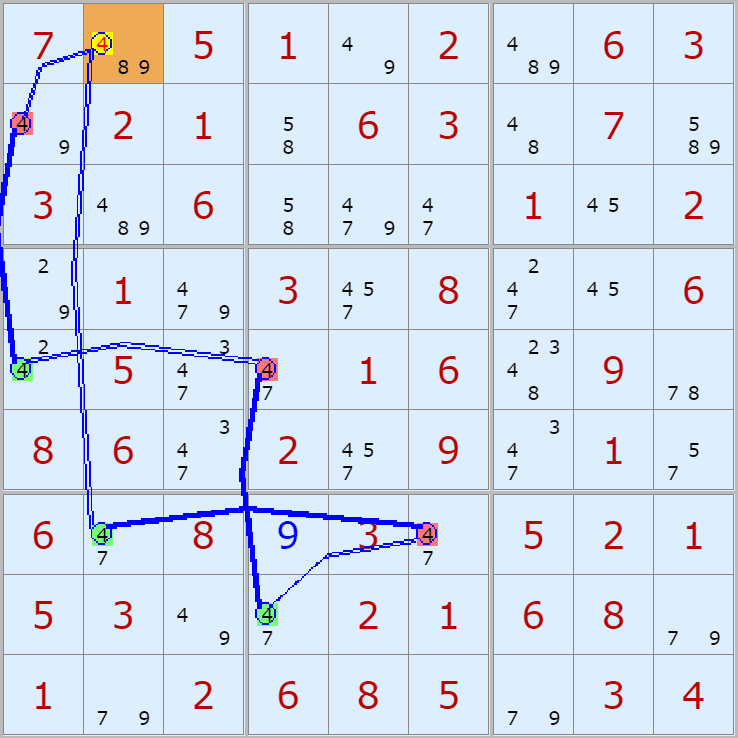
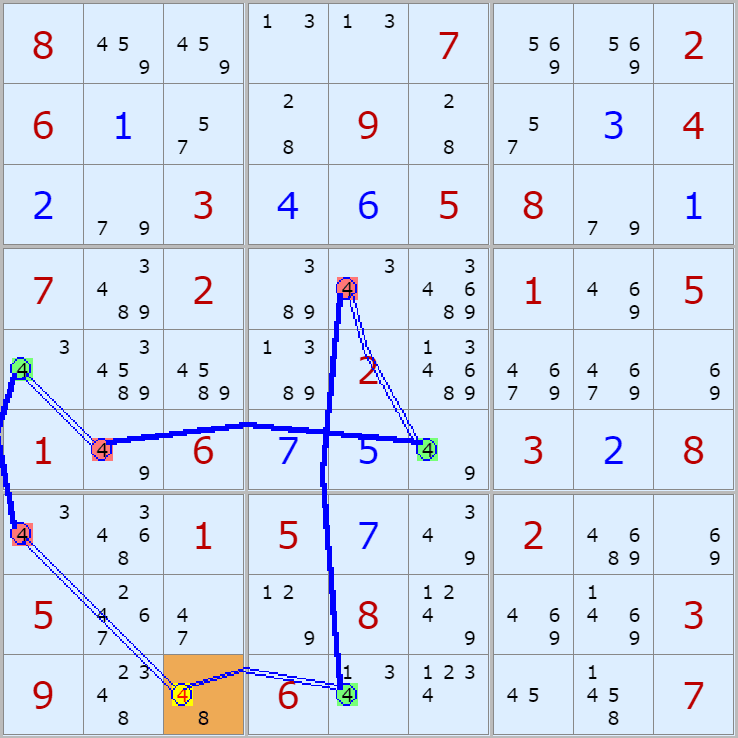
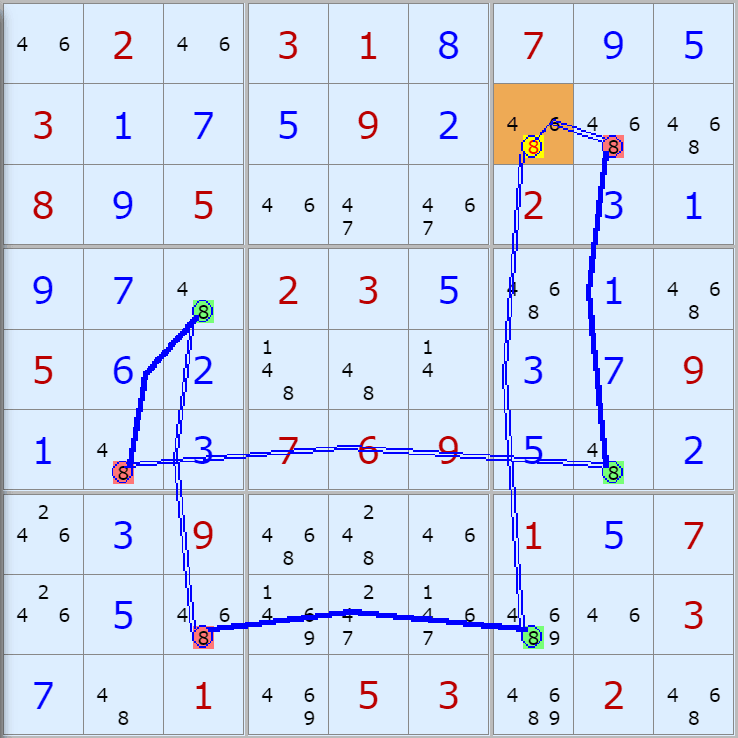
'스도쿠 위키'라는 사이트에서 예제를 좀 모아 봤다(루프형 19개, 위크 링크형 87개). X사이클은 막혔을 때, 판을 뚫어 주는 트리거 역할을 하는 좋은 공식이므로 부디 많이 보고 체득하기를 바란다. 예제는 아래 더보기를 누르면 된다.(스크롤 하지 말고 사진을 터치 또는 클릭하면 사진만 한장씩 볼 수 있다.)

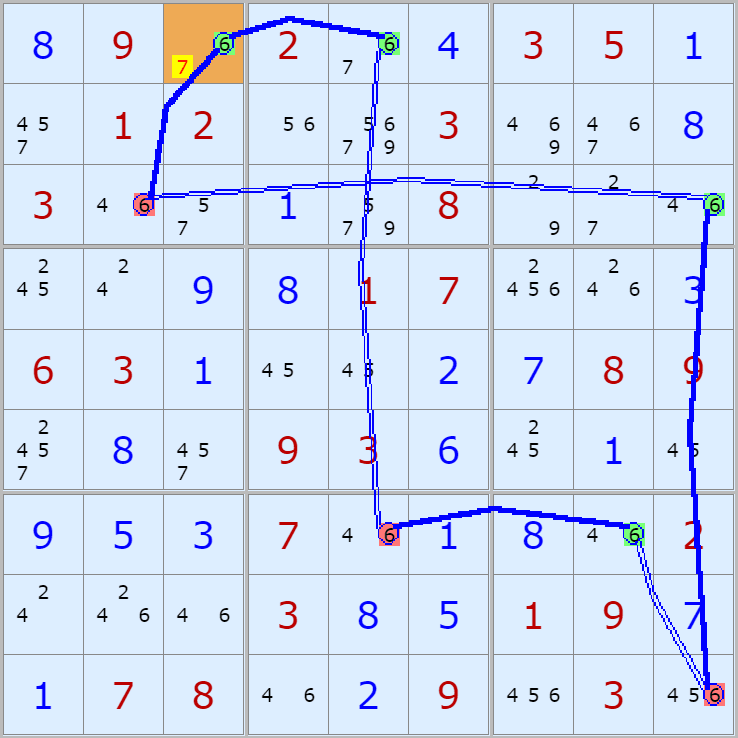
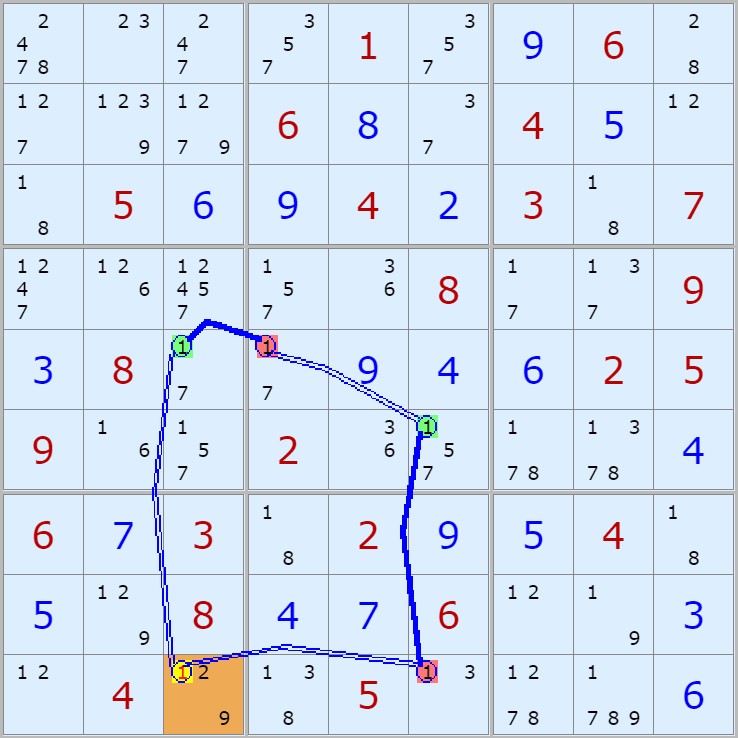
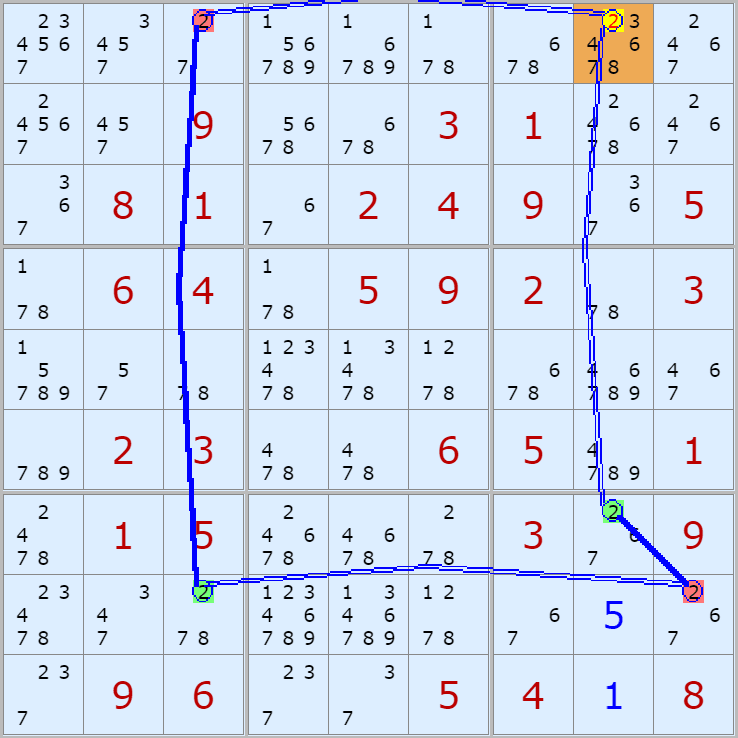
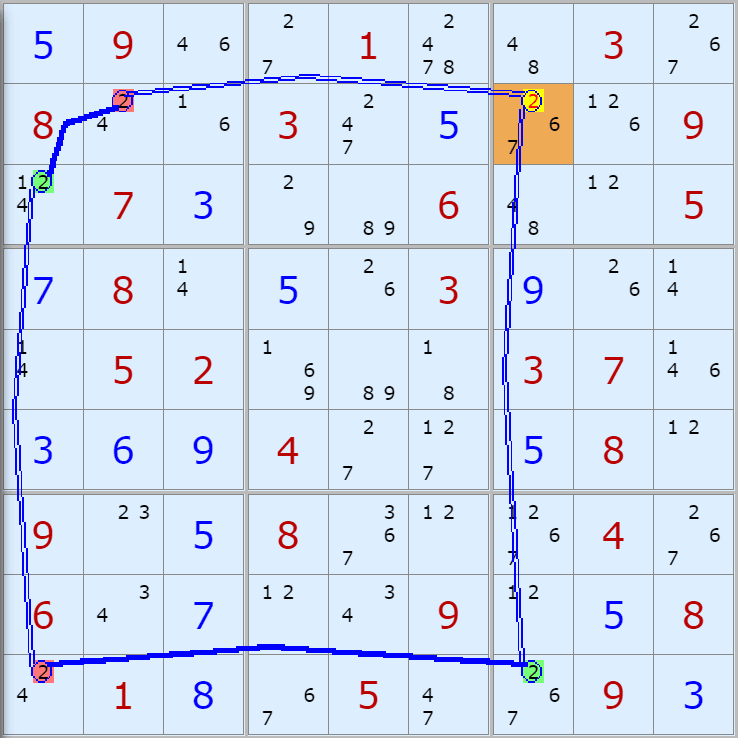
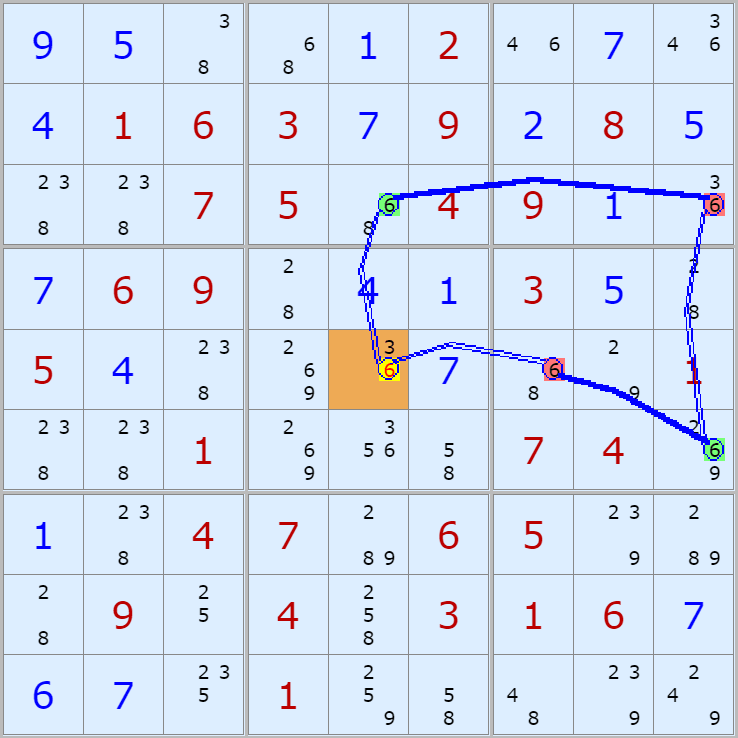
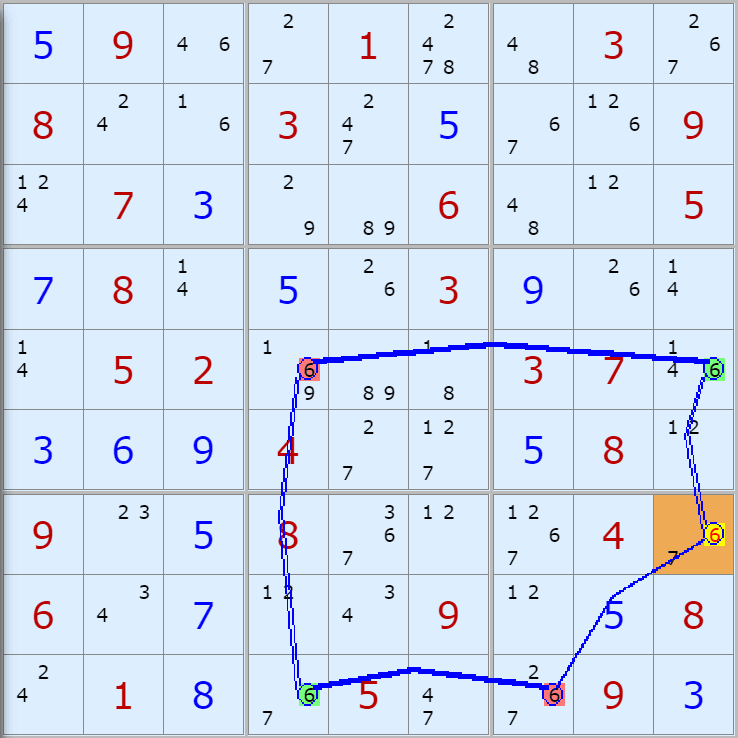
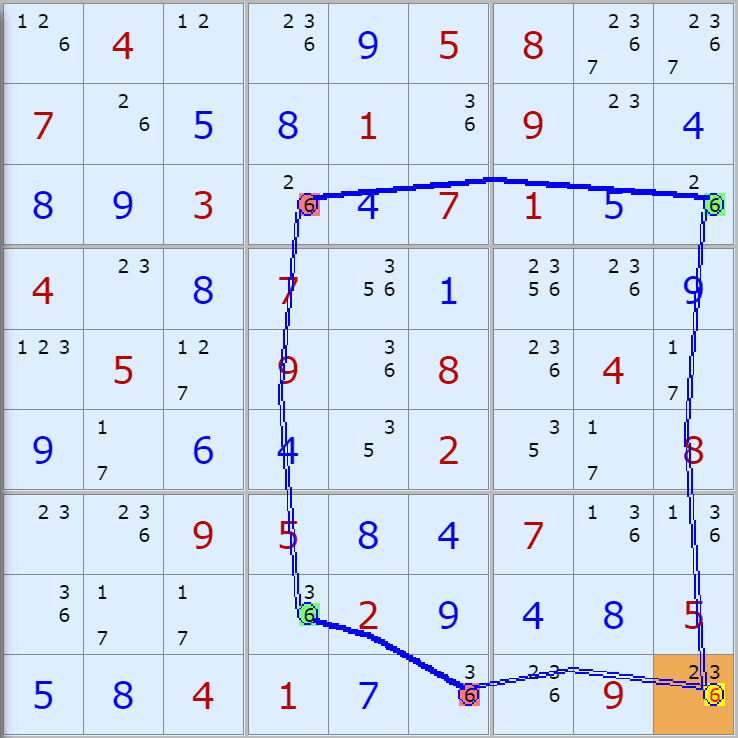
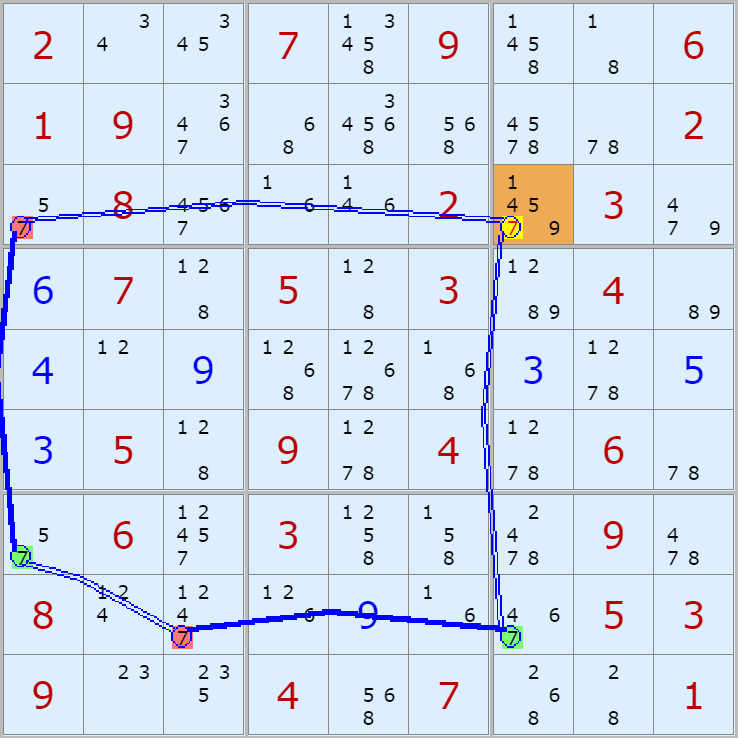
자료를 읽은 방법은

보통 상단부 또는 좌측에 위치한

연두색 후보수가 시작점(off)이 되고

마지막 빨간색 후보수가 끝점(on)이 된다.

또한 노란색 후보수가 제거되는 후보수이다.

링크를 연결하는 굵은색 실선은 스트롱 링크

이중실선은 위크 링크이다.