스도쿠 15. 고급공식/ 싱글 체인(심플 컬러링)-움짤, 패턴
- 스도쿠/고급
- 2024. 10. 6.
스도쿠 기술이 초급에 머물러 있는 스린이(=스도쿠 어린이)인 나는 계속 비슷한 초급 기술만 쓰니까... 스도쿠가 좀 무료해 지고 있던 찰라였는데 아래와 같은 난제가 찾아 왔다. 셀1-67페어, 48페어, 셀2-숨겨진 숫자를 못 찾겠음, 셀3-확정숫자 6은 딱히 힘이 없고 36페어, 58 페어, 셀5-트리플, 셀6-37페어, 셀8은 쿼드러플, 마지막 셀9-37페어.....
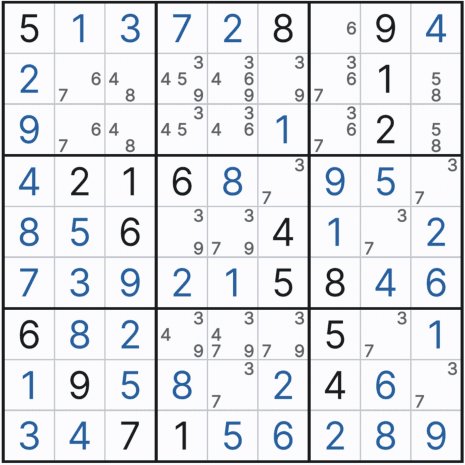
보통 10분 이내에 풀던 난이도에서

페어, 트리플, 쿼드러플 지옥에서 25분까지 헤메이다가... 번뜩~ 눈에 띄는 숫자들에서 싱글 체인을 써 먹을 때가 드디어 온 것을 느꼈다. 싱글 체인을 익힌 후에 눈에 불을 키고 찾아 보려고 게임을 했지만 조건에 맞는 상황이 한 번도 없었다.
아래는 싱글 체인(Single Chain) 공식이 트리거가 되어 판을 일사천리로 깬 기록을 움짤로 만들어 봤다. 뒤에 설명을 할테니 싱글 체인을 몰라도 일단 흐름만 보자!

위의 움짤에서 후보숫자 3을 연결 시킬 때, 색을 번갈아 썼는데 보통 이렇게 색을 2가지를 써서 스도쿠를 설명한다고 해서, 싱글 체인을 심플 컬러링(체인)이라고도 부른다고 한다. 이렇게 단일 후보숫자 X를 사용하는 X-Chain을 Single Chain이라고 부른다.
이제 본격적으로 체인의 세계로 한 발 내 딛어 보자.
1. 링크. 같은 후보숫자가 있는 두 개의 칸이 연결되어 있는 것을 링크라고 한다. 링크는 아래와 같이 같은 후보숫자를 직선 또는 사선으로 연결한다.

링크에는 스트롱 링크와 위크 링크가 있는데..

스트롱 링크 - 위의 그림과 같이 한칸이 (2,2)칸이 7이라면 링크된 (1,3)칸이 3이 되고, (2,2)칸이 3이라면 (1,3)칸은 무조건 7이되는 참(On), 거짓(Off) 가되는 링크를 스트롱 링크라고 한다. 보통 설명할 때는 실선으로 나타낸다.
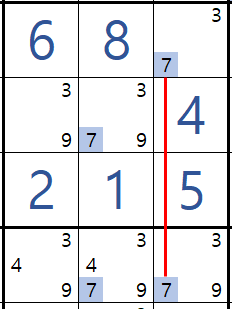
위크 링크 - (1,3) 칸이 7이라면 (4,3)칸은 3 또는 9가 되고, (1,3) 칸이 3이라면 7 또는 9가 되는 조건부 링크를 위크 링크라고 부른다. 또한 위크 링크의 형태가 또 하나 더 있는데.. 설명할 때는 점선으로 나타낸다.

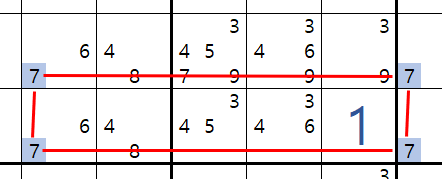
위의 그림과 같이 한 행(또는 열)에 동일한 후보 숫자가 3개 이상 있는 경우에 연결되는 링크를 위크링크라고 한다. 이 말은 만약 (1,1)칸이 7이라면 (1,3), (1,6)칸은 무조건 7이 제거(off)되는데 반해 / (1,1)칸이 6이라면 (1,3), (1,6) 둘 중에 한 칸에 오는 조건부 링크라서 위크링크라고 부른다.
고급 체인 기술로 가면 스트롱 링크와 위크 링크의 배열에 따라 답이 달라지는 경우도 있다. 뒤에 나오는 예제에서 확실하게 스트롱 링크를 보는 것을 익혀보자. 하우스안에 2개의 후보수만 있는 것을 보는 게 뭐가 대수냐 싶겠지만, 실제 게임을 하면 체인으로 엮으면 잘 안 보인다.
위의 링크를 복수로 연결하는 모양을 쇠사슬을 닮았다고 하여 체인이라고 부른다.

위와 같이 링크를 엮어 가는 것을 체인이라고 부르는데, 셀1~3에 보면 우리에게 익숙한 X윙도 링크의 체인으로 엮어 있음을 알 수 있다.
다만 X윙은 싱글 체인은 아니고 X-Cycle이라고 부르는 공식인데, 나중에 자세히 알아 보자!
또한 체인을 이루는 행과 열에는 동일한 후보숫자 7이 올수 없음을 직관적으로 알 수 있다. 위의 그림에서 하부의 링크들을 보면 젤리 피쉬의 형태임을 알 수 있다.

젤리피쉬도 싱글 체인은 아니니 나중에~ 깊숙히 알아 보자.
위의 그림을 보면
1. 직선 링크는 90도로 꺾이며 연결 되면서 체인을 이룬다. (직전으로 연결하면 위크 링크가 되면서 조건부 링크가 되어 무조건 참인 답을 도출할 수 없다. 동일한 하우스 안에 3개 이상의 칸이 있다면 직선으로 연결 되지 않는다. 90도로 꺾이는 링크 또는 사선으로 연결되는 링크로 연결한다.
2. 사선 링크는 동일한 하우스에 위치한 링크만 연결 가능하다. 다른 셀의 칸끼리는 사선으로 연결 되지 않는다.
다.
추가 > 실제로 게임을 하다보면 위의 그림과 같이 선을 긋지 않고 숫자들로만 판별을 해야해서 잘 보이지 않는다. 추후에 더 고급 체인 기술로 들어가면 스트롱 링크와 위크 링크에 의해 결과값이 달라질 수도 있기 때문에 링크를 정확히 보는 것이 중요한데, 모든 상황의 스트롱 링크와 행과 열에 있는 위크 링크는 판별이 쉬운 반면에 박스(=블록)안에 있는 위크 링크는 행과 열에 대한 것이 혼재 되어 잘 보이지 않는다.
그래서 아래 움짤을 만들어 봤다. 박스 안의 위크링크에 집중해서 보자. (빨간생:스트롱 링크, 보라색:위크 링크)

스도쿠 위키라는 사이트에 가면 사이트가 인터페이스가 어지럽긴 하지만 매우 좋은 사이트다. 문제를 풀어 주는 기능도 좋고(입력한 문제에 쓰인 공식까지 분석해서 시각적으로 보여 준다.), 각 공식별 예제를 봐도 좋은데 체인과 관련된 이야기를 하면 아래와 같이 스도쿠 게임의 각 숫자별 링크 및 체인 상황을 보여 주는 것을 들여다 보면 좋을 거 같다. 좌측 하단의 Boxes를 누르면 셀의 링크, Rows를 누르면 행의 링크, Columns를 누르면 열의 링크를 보여 주고 각각 따로 보거나 합쳐서 볼수도 있다.

자 이제 드디어 본격적으로 기본 체인 공식인 싱글 체인에 대해 움짤을 보면서 알아 보자!!
싱글체인은 중반에 확실한 페어가 눈에 많이 띄일 때 적용을 검토하는 것이 좋다.
움짤을 보면서 반복해서 설명하겠지만 싱글 체인의 기본적인 규칙은 아래와 같다.
- 싱글 체인은 엑스 사이클(X-Cycles)의 하위 개념으로 조건부 X-Cycles Chain이라고 보면 된다.
- 한 개의 하우스 안에는 한 개의 링크만 존재=모든 링크가 스트롱 링크로만 이루어져 있다는 것을 의미한다.
- 체인의 추적은 2개의 후보숫자가 들어 있는 칸에서 시작한다. (3개 이상의 칸은 시작점을 찾기가 힘들다.)
- 또한 시작칸의 스타트는 '만약에 후보숫자 X가 아니라면'이라는 가정으로 출발한다. (뒤에 설명하겠지만 On이면 굳이 체이닝을 할 필요가 없이 한 가지의 답이 바로 나온다.)
- 체이닝은 시작점과 끝점이 마주보는(=크로스 되는) 지점까지 추적해서 연결한다.
- 시작점과 끝점을 바꿔도 결과는 똑같다.
- 시작점과 끝점이 동시에 바라보는 칸의 후보숫자를 지울 수 있다.
- 체인을 구성할 때, 동일한 시작점에서 끝점을 가는데 1개를 초과하는 복수의 경로가 있을 수도 있다.
표기법은
- 색을 두 가지로 사용하여 링크를 번갈아 가며 칠을 한다.
- 스트롱 링크는 실선, 위크 링크는 점선을 사용하거나 다른 2가지의 색으로 표기한다.
싱글 체인 예제.
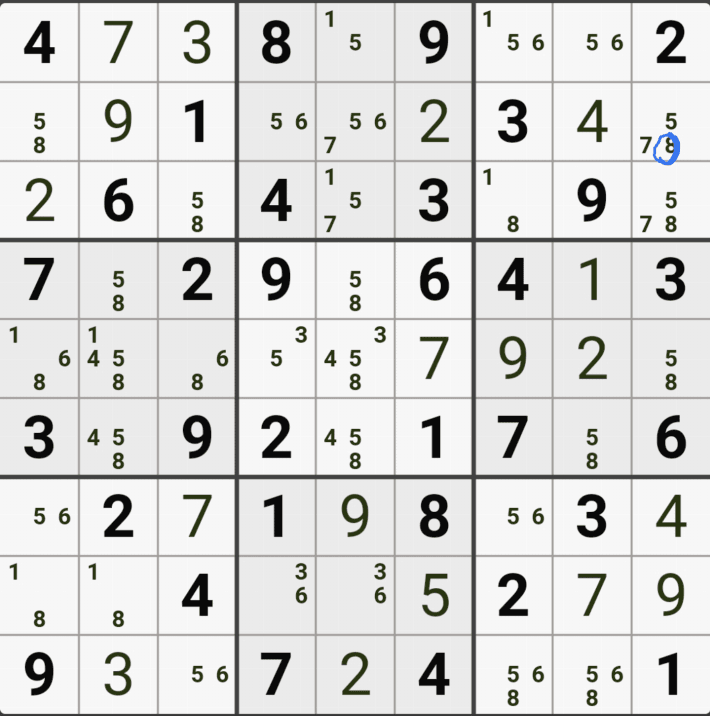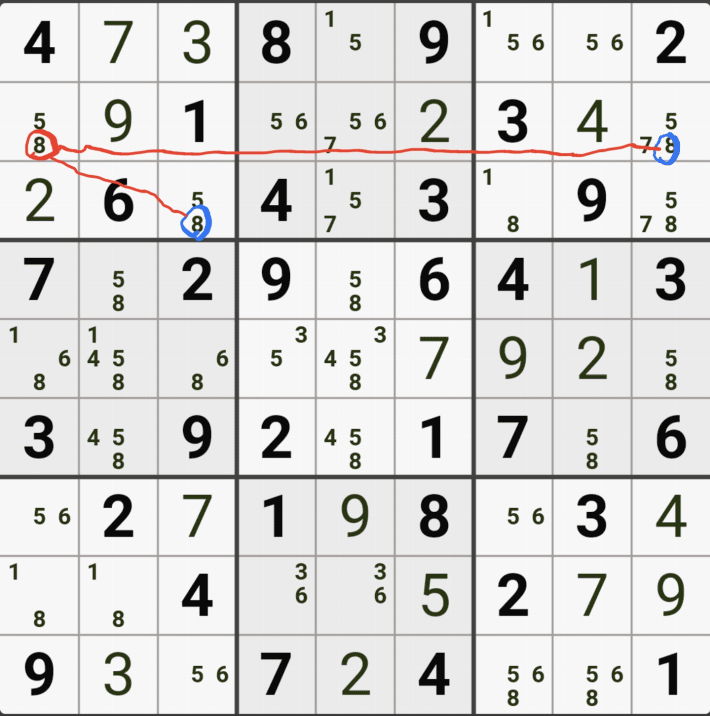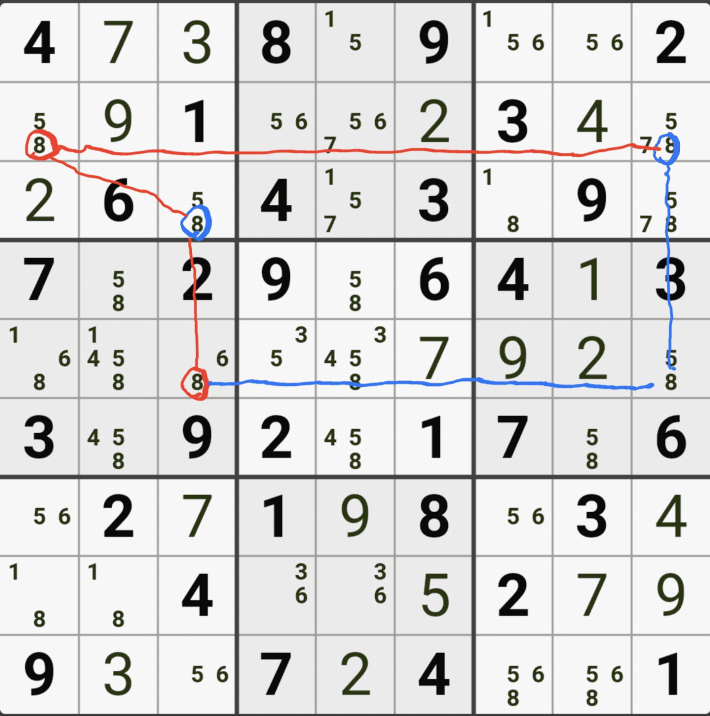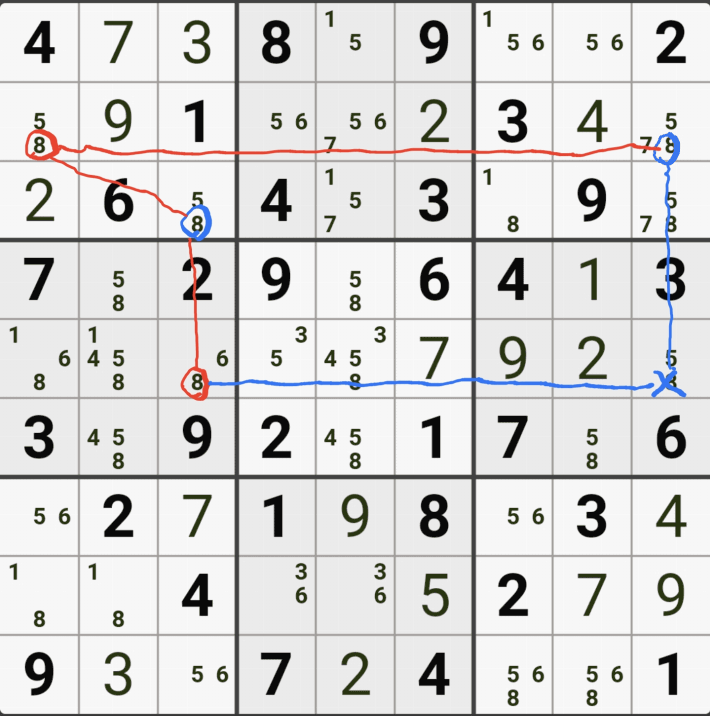
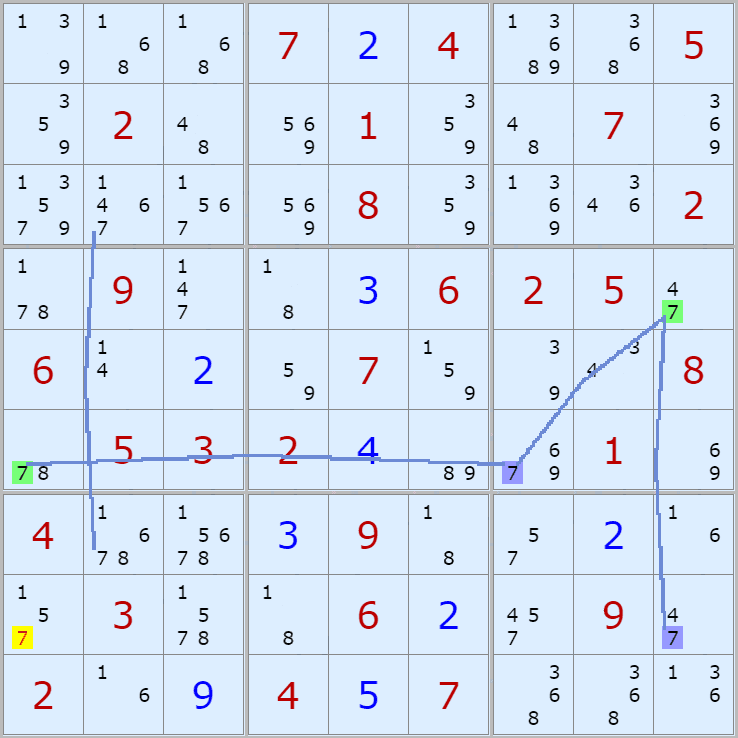
처음에 봤던 싱글체인 공식을 쓴 움짤을 설명하겠다.

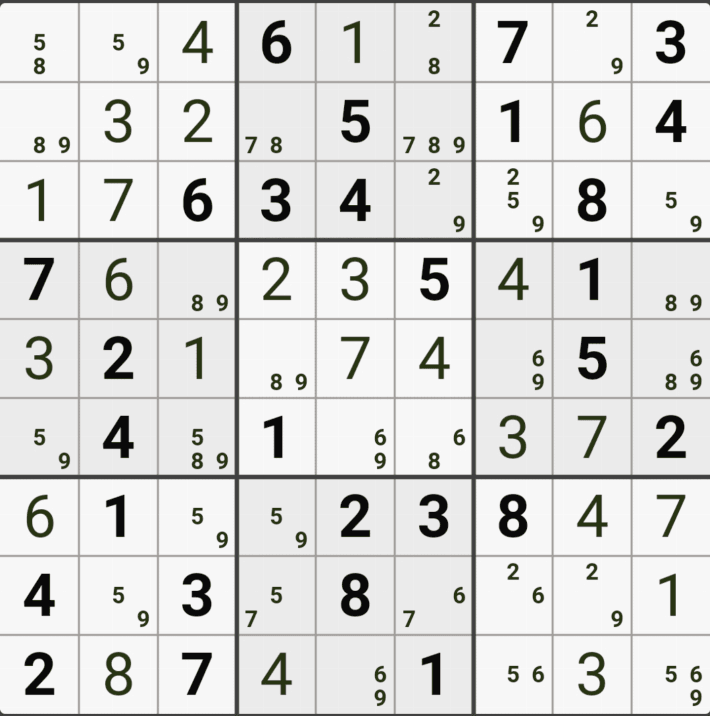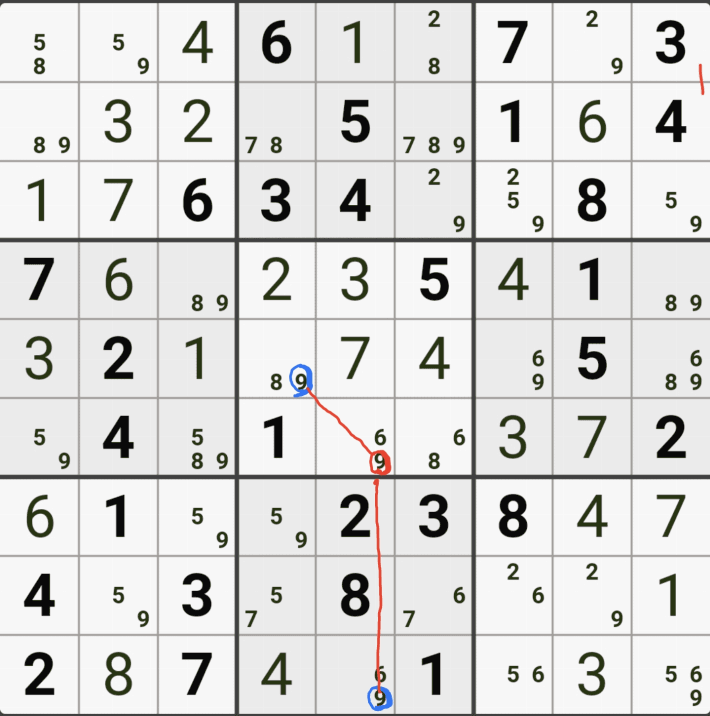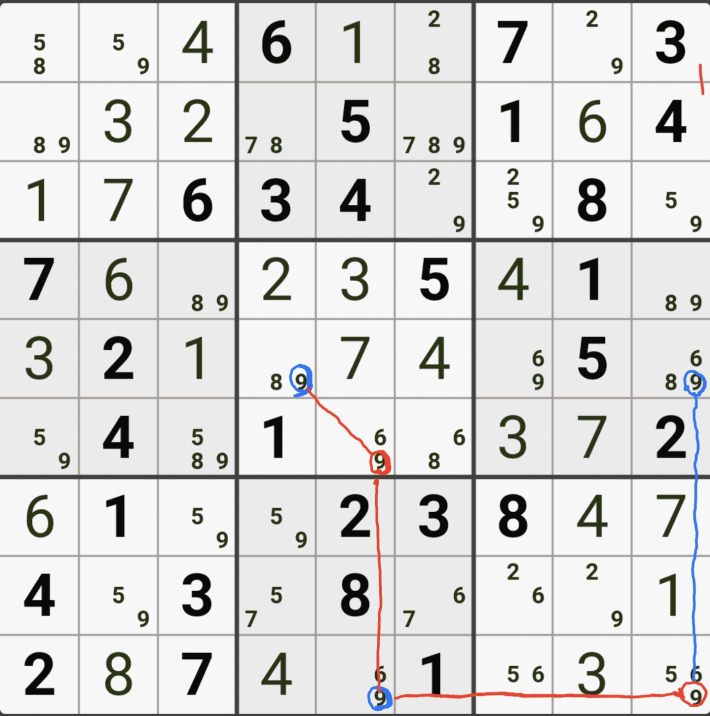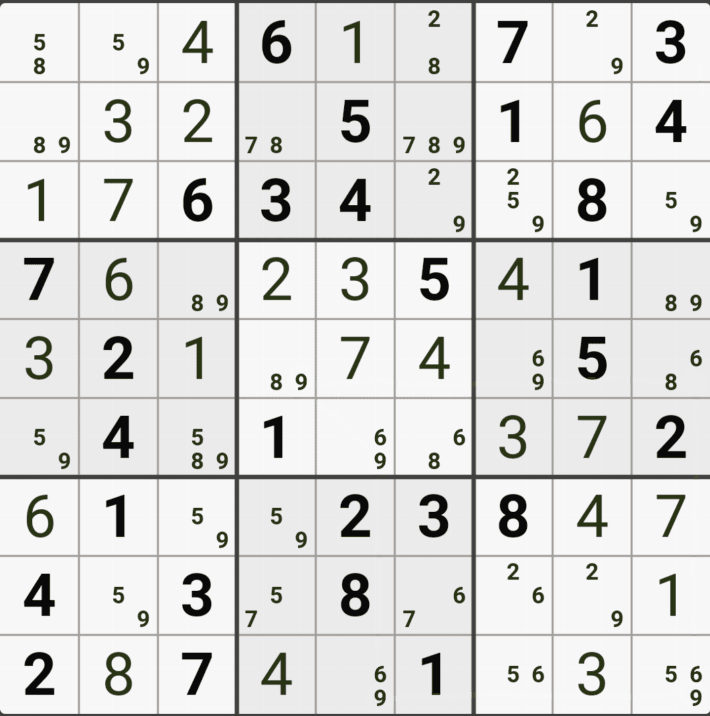
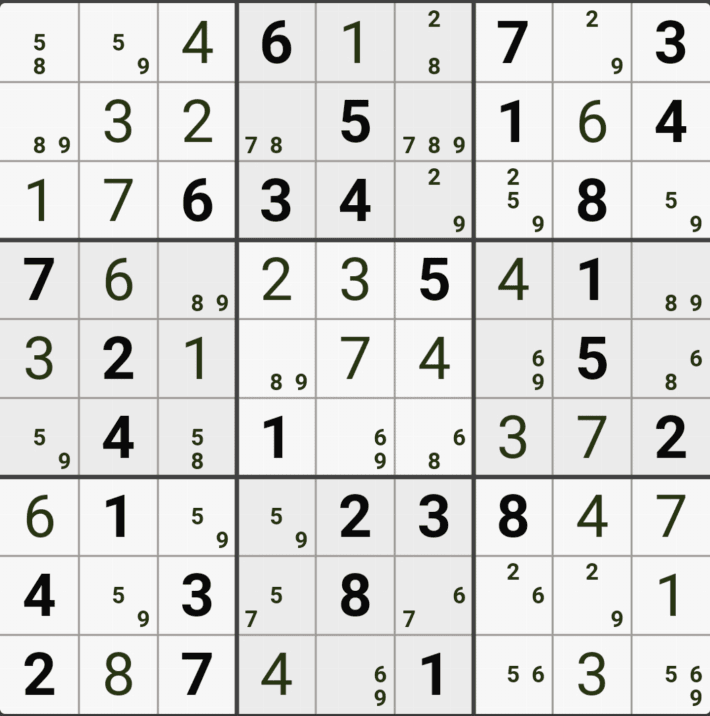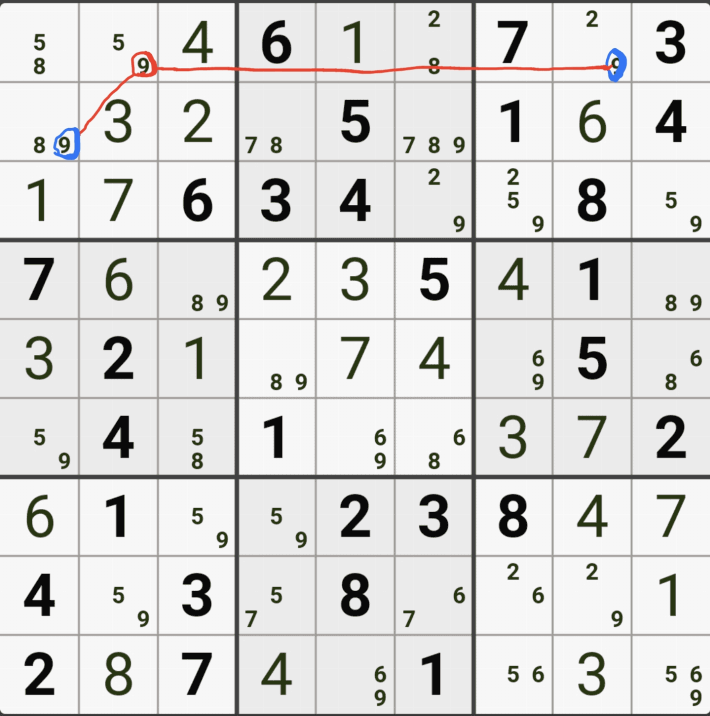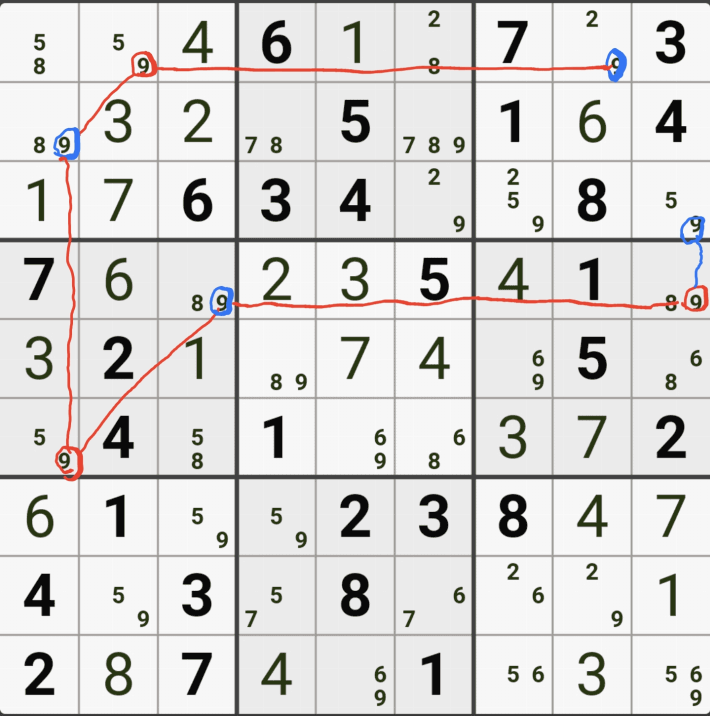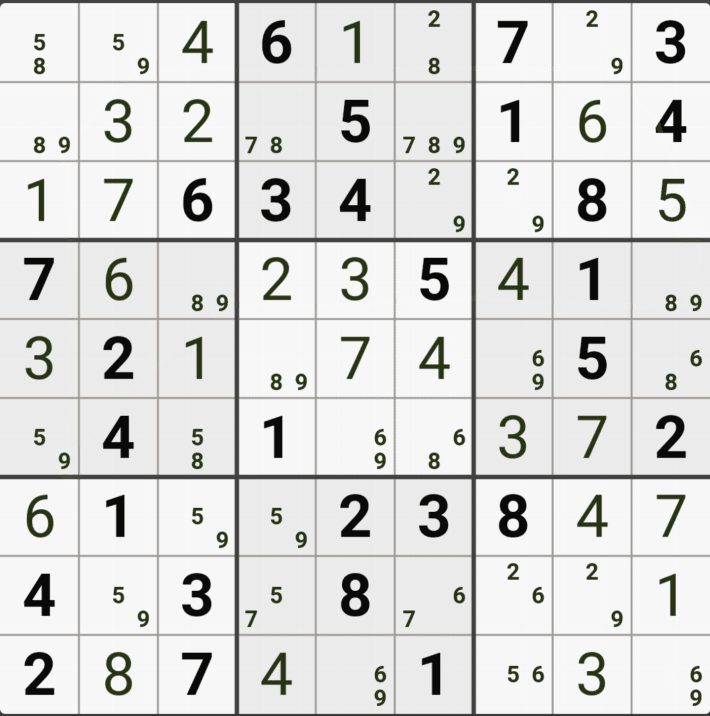
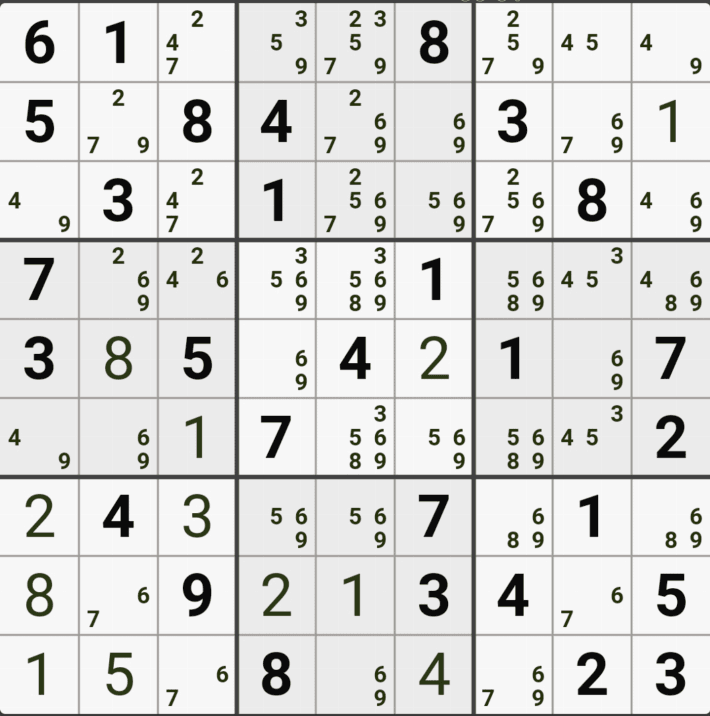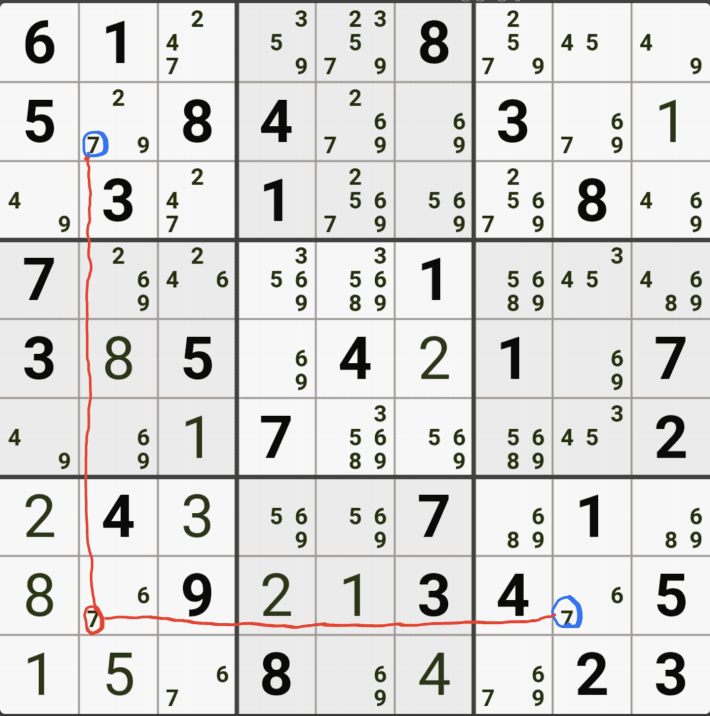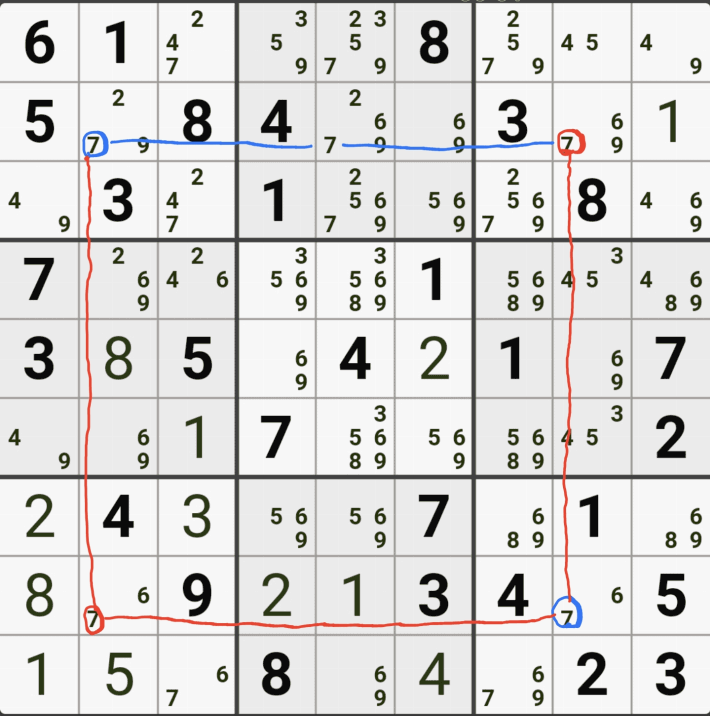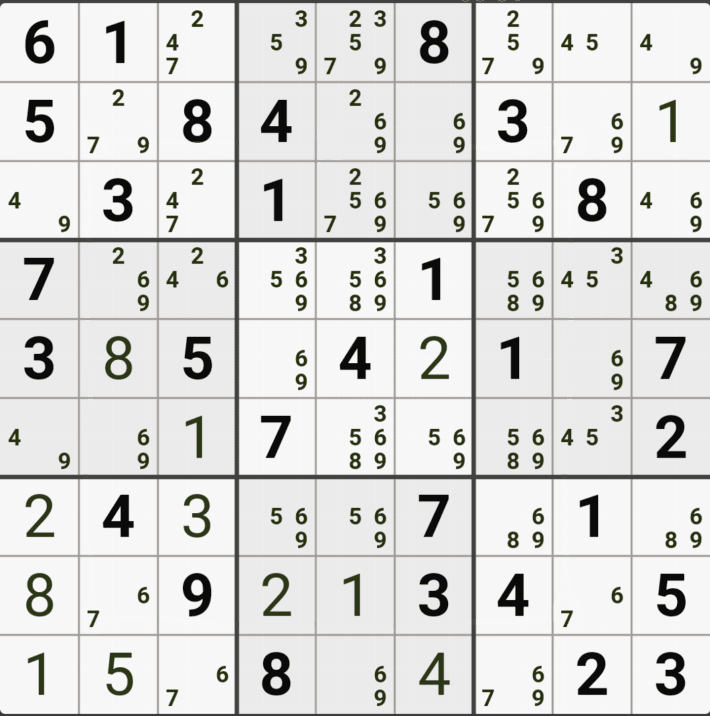
위의 움짤은
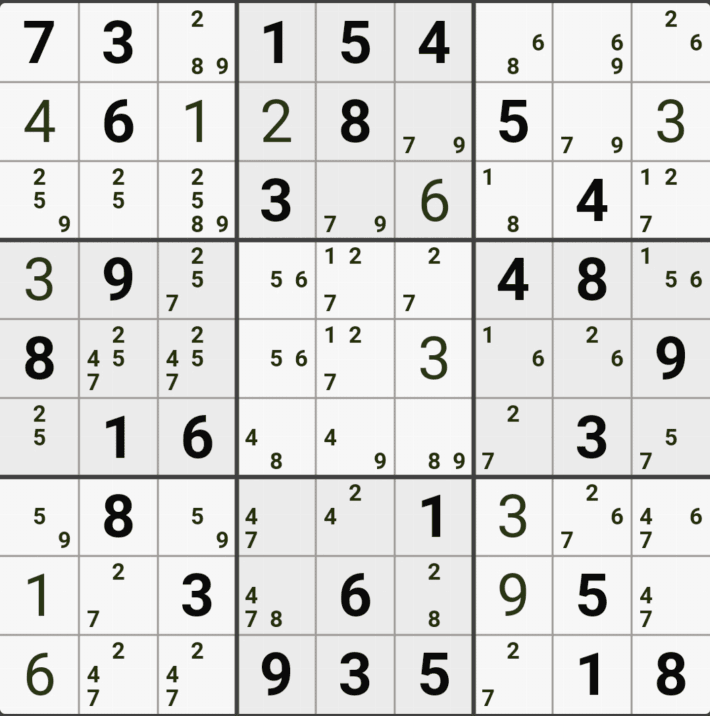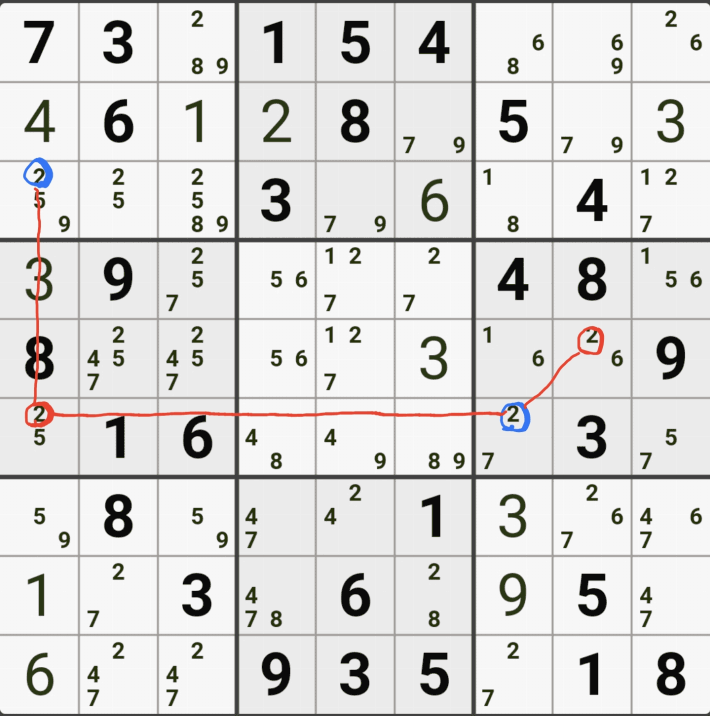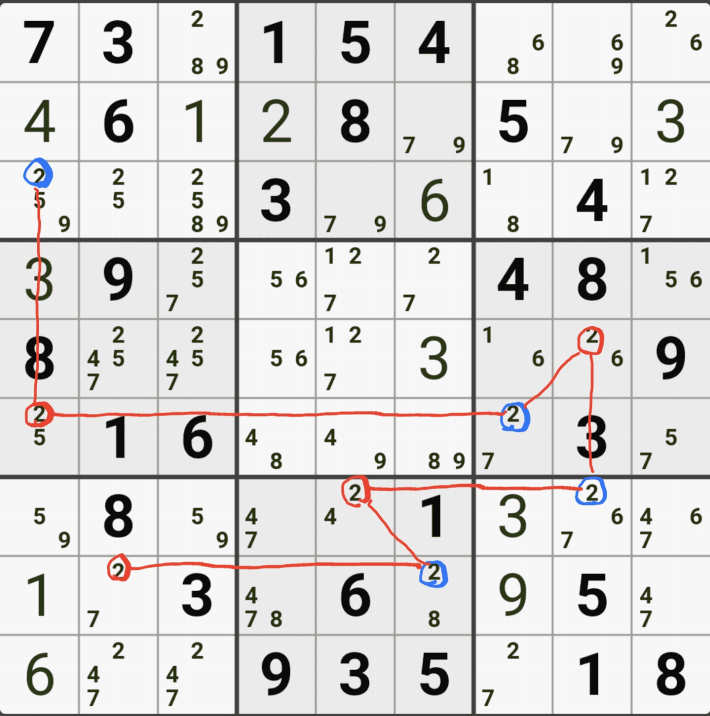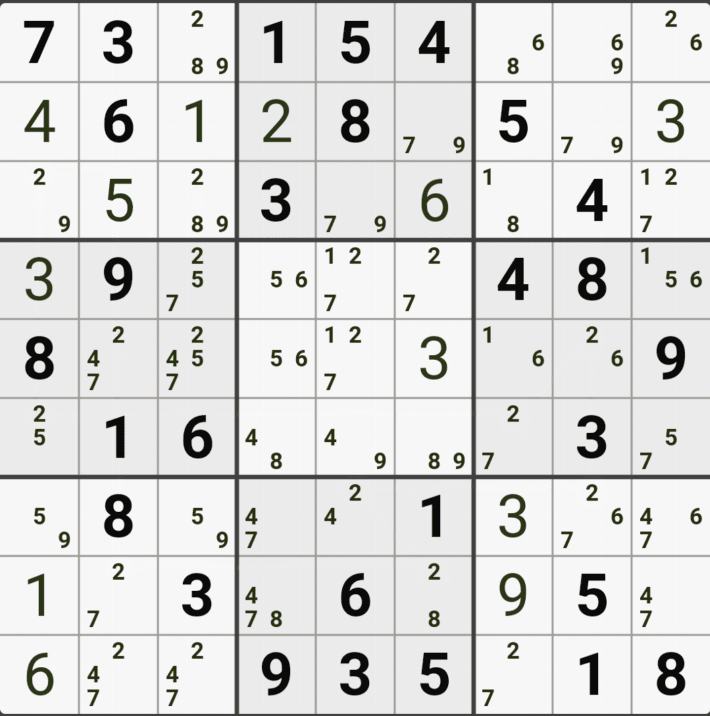
(4,6)의 칸이 3이 아니라면 (4,9)는 3이 되고,
(8,9)는 3이 아니고,
(8,5)칸은 3이 확정 되므로
(8,5) 와 (4,6) 두 칸이 동시에 마주보는 (5,5)칸의 후보숫자 3을 지울 수 있다.
응? 근데 뭔가 좀 이상할 것이다. (4,6) 3이라는 가정은 왜 없나? 라는 생각이 들 것인데 말로 먼저 설명하면 그 가정은 이미 증명이 되어 있기 때문에 생략하는 것이다. 무슨 말인지 또 움짤로 설명하겠다.
경우의 수 1. (4,6)이 3이라면

위의 움짤과 같이 같은 셀에 있는 (5,4), (5,5) 두 칸의 후보숫자 3을 제거 할 수 있다.
경우의 수 2. (4,6)이 3이 아니라면(=7이라면)

위의 움짤 처럼 (4,6)이 3이 아니라면 (8,5)칸이 3이 되고, 같은 셀에 있는 후보숫자 3 전체와 5열에 위치한 수보숫자 3 모두를 제거할 수 있는 것을 알 수 있다.
즉 어떠한 경우라도 후보숫자 3이 제거 될 수 있는 지점은 (4,6)과 (8,5)가 마주보는 (5,5)의 후보숫자 3이다. 직관적으로 알 수 있게 위의 2가지 경우의 결과만 움짤로 만들어 봤다.
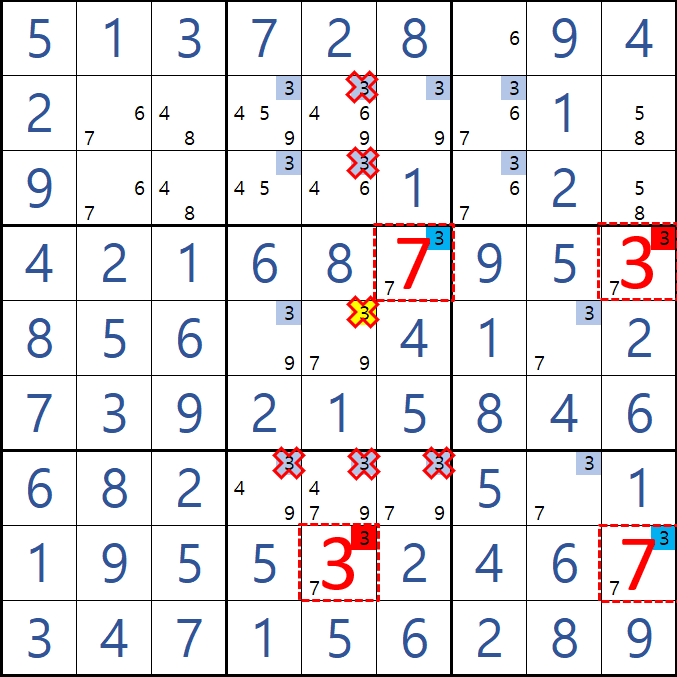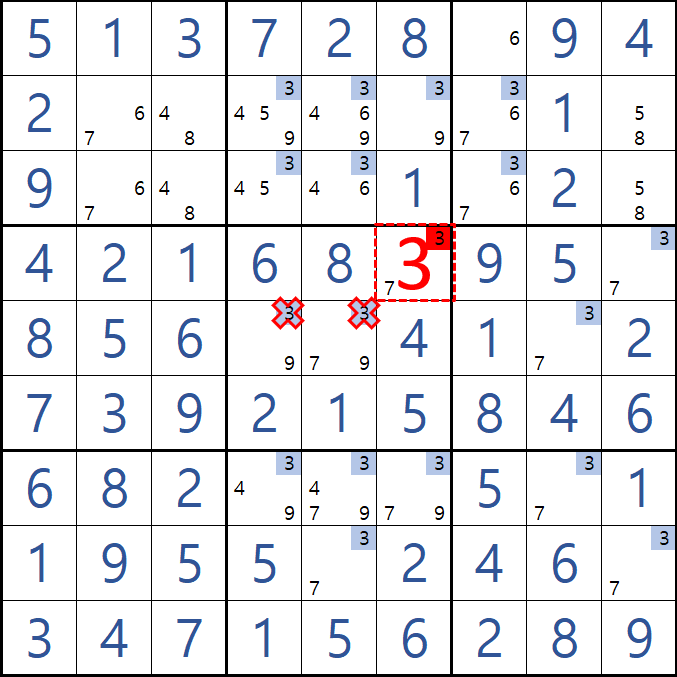
그래서 앞으로는 항상 '후보숫자 X가 아니라면'이라는 경우만 설명 또는 도식화 할 것(싱글 체인 뿐만 아니라 모든 체인의 시작이라고 봐도 무방하다.) 이고 위와 같이 숫자를 사용하기 보다는 직관적으로 볼 수 있는 아래와 같은 다이아그램 형식의 그림으로 표현할 것이다. (나의 방법은 아니고 스도쿠계의 관행인 거 같아 보이고, 나도 직관적이라 보기 좋다.) 또한 모든 것을 움짤로 만들기에는 시간도 많이 걸려서 아깝기도 하고 아래의 그림 처럼 한장으로 서로 교감할 수 있다는 것도 합리적이라고 본다.

위와 같은 싱글 체인 풀이법을 읽는 방법은 간단하다. 노란색(=제거 될 후보숫자)과 가까운 파란색이 스타트 지점이고 파랑(off) > 빨강(on) > 파랑 > 빨간색(끝점)으로 파랑과 빨강이 마주 보는 칸의 후보숫자가 제거 된다로 이해 하면 되겠다. 그래서 글로 (3,5)칸의 후보숫자 뭐는 ..... 같은 긴 설명이 필요 없다. 위의 그림과 같이 시작점과 끝점이 마주보는 3을 지울 수 있다. 정도면 모두 알 수 있기 때문이다.
그리고 위의 그림처럼 다이아그램으로 표기 하는 이유 중에 하나는 아래와 같이 체인이 형성 되는 길이 하나가 아니기 때문이다. 같은 점을 가는 경로가 아래와 같이 3가지가 있어서 복수의 갯수로 생기는 경로를 한 그림에 표기하면 인사이트를 얻기에도 좋다. (물론 실전에서는 최단 경로를 추적해 나간다.
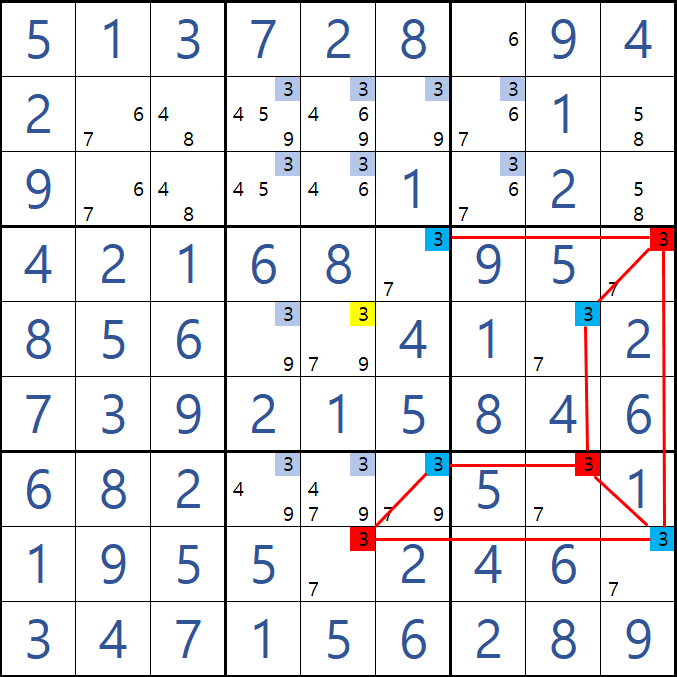
또한 위의 그림에서 중요한 점 하나를 말하자면 어떤 경로로 체인을 구성하던지 모든 길에서의 On, Off의 위치는 동일해야 한다. (복수의 길이 있을 때는 확실히 하기 위해 검산이 가능하다는 장점도 있다.)
스도쿠를 좀 알아가다 보니까. 기술을 이해 하는 것도 중요하지만 공식이 쓰인 사례를 많이 봐야 한다고 생각한다. 의외로 싱글체인은 만나기가 어렵다. 그래서 잘 보이지 않는다.
이 글을 보는 이들이 싱글 체인에 익숙해 지도록 싱글 체인 사례를 '스도쿠 위키'라는 사이트 https://www.sudokuwiki.org/Sudoku.htm 에서 모아봤다 (운영자에게 매우 고맙게 생각한다~). 아래 움짤은 스도쿠 위키에서 모은 사례 46가지를 움짤로 엮은 것이고, 아래 더 보기를 누르면 각 사례의 그림을 볼 수 있다.

사례들의 범례를 간단히 설명하면
노란색 = 제거될 후보숫자
연두색 = 싱글 체인 시작점
보라색 = 싱글 체인 종착점
복수의 선은 여러가지 경로가 있음을 나타내고, 제거될 숫자인 노란색이 1개를 초과 한다는 것은 같은 게임안에 동일한 후보 숫자의 경로가 여러가지 있다는 것을 의미하는데, 보통 여러개의 답이 있어도 1개만 확정숫자를 찾으면 트리거가 되는 경우가 많아서 눈에 잘 띄고 최단 거리에 몰려 있는 것 위주로 보면 좋을 것이다. 처음에는 헷갈릴 수 있으니 여러개의 사례가 있는 노란색이 2개 이상인 그림은 건너 뛰는 것도 좋을 것 같다.
끝으로 하나만 더 이야기 하겠다.
싱글 체인의 형제 격인 X 체인이라는 공식(따로 글은 쓰지 않겠다.)이 있는데, 싱글체인과 조건이 다 같은데 한 가지 다른 점은 싱글체인은 모두 스트롱 링크로 연결 되는데 반해서 X 체인은 스트롱 링크(시작점) + 위크 링크 +.....+ 스트롱 링크 (끝점)가 교대로 조합되어 보통 아래와 같은 형태로 나타난다.
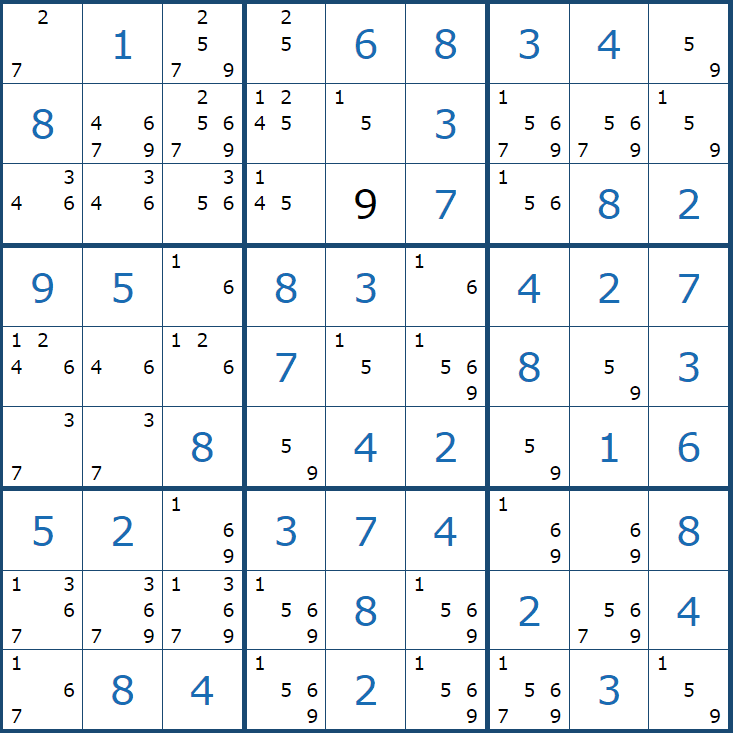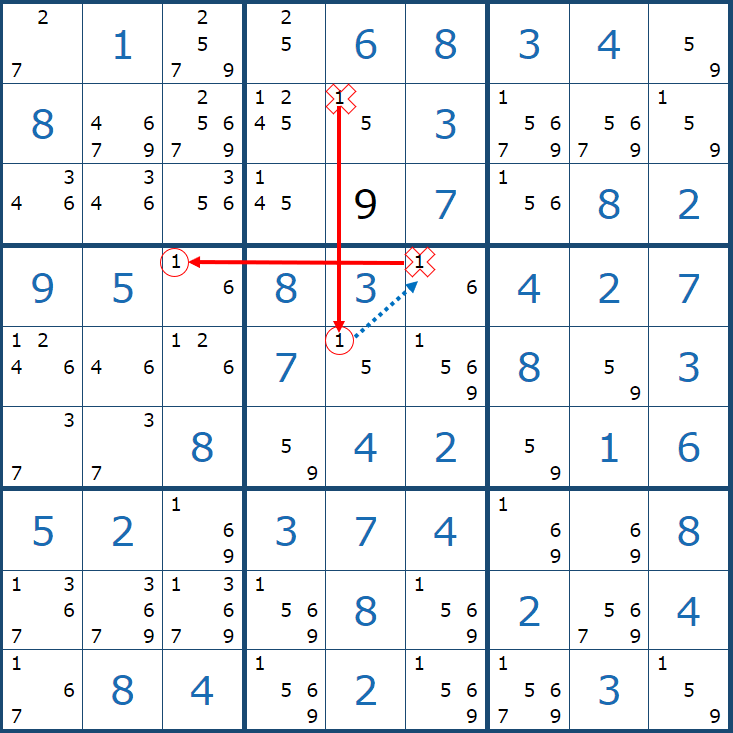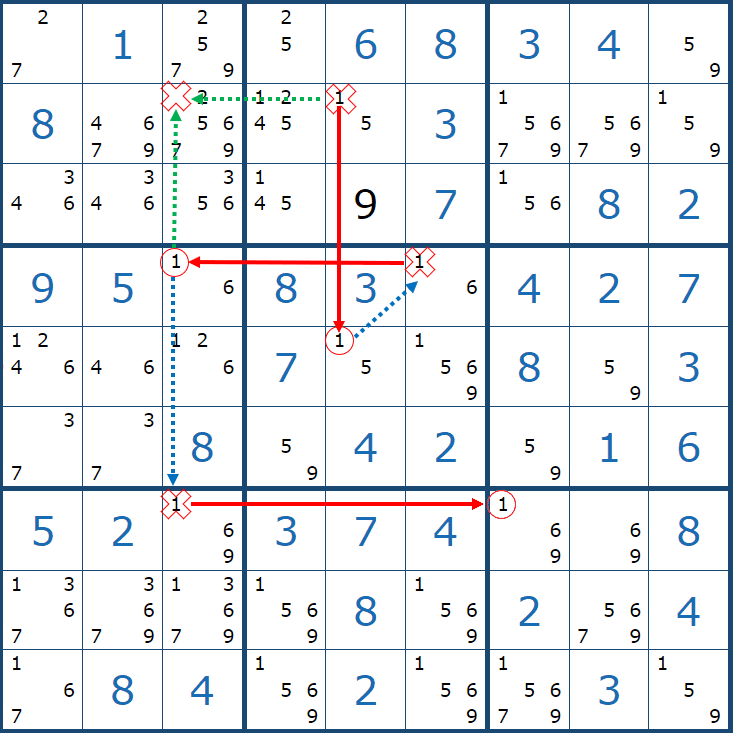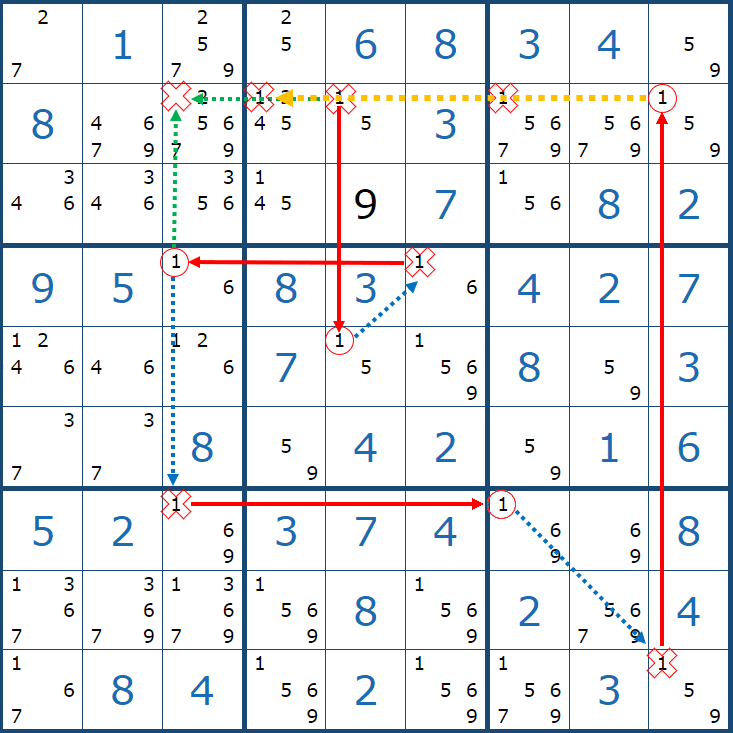
설명을 하지 않아도 무슨 뜻인지 알 거라고 생각한다. 위크 링크만 신경 쓰지 않고 후보숫자 1에만 집중하면 싱글 체인과 작동 원리가 똑같다. X체인의 경우의 수는 아래와 같다.

모쪼록 익숙해 져서 싱글 체인 상황이 오면 잘 캐취해서 더욱 더 재미 있는 게임 라이프를 즐기기 바란다.
싱글 체인 다이아그램 예제
초반 몇 개는 함께 읽어 보자.
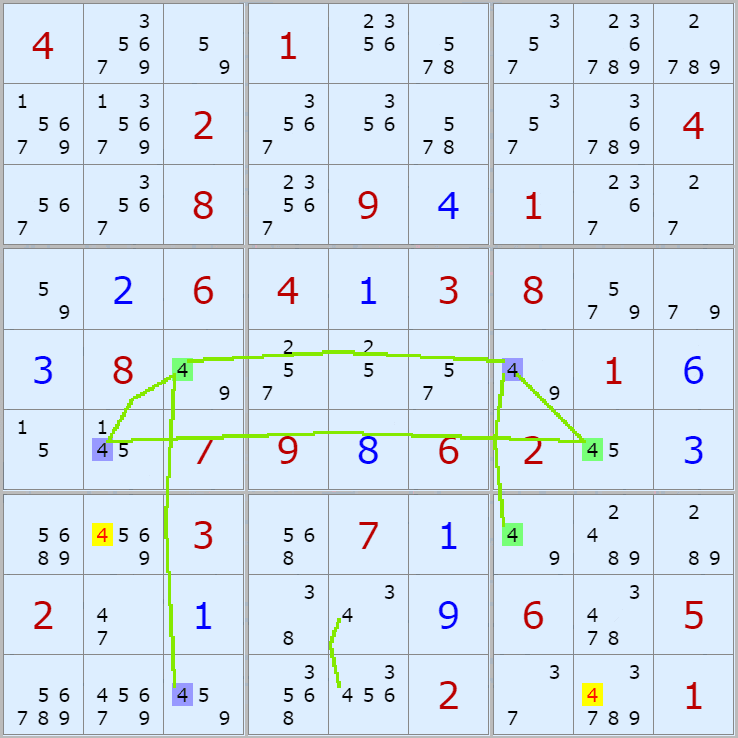
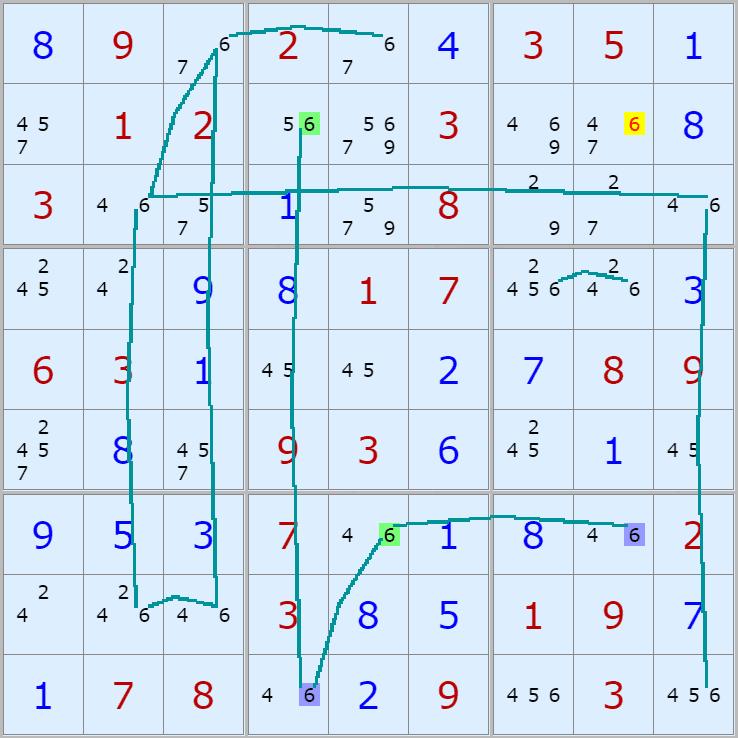
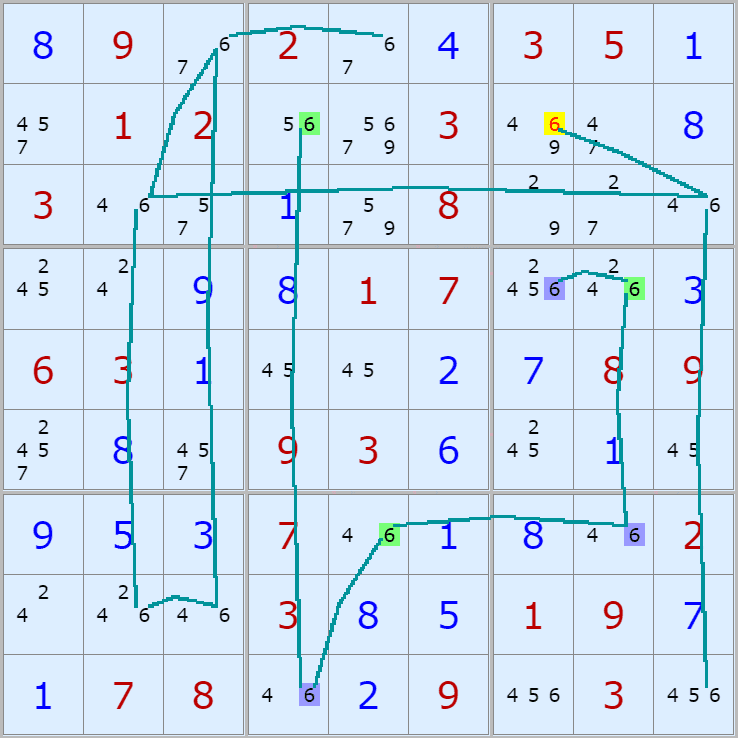
001.

(1,6)칸이 8이 아니라면
(1,8) On > (5,8) Off > (5,2) On > (9,2) Off > 끝점 (9,6)이 On 이 되며
(1,6)과 마주보는 칸 안에 있는
(3,6), (7,6) 2칸에 있는 후보숫자 8을 2개 지울 수 있다.
경로는 2개를 초과하는 복수의 갯수가 있다.

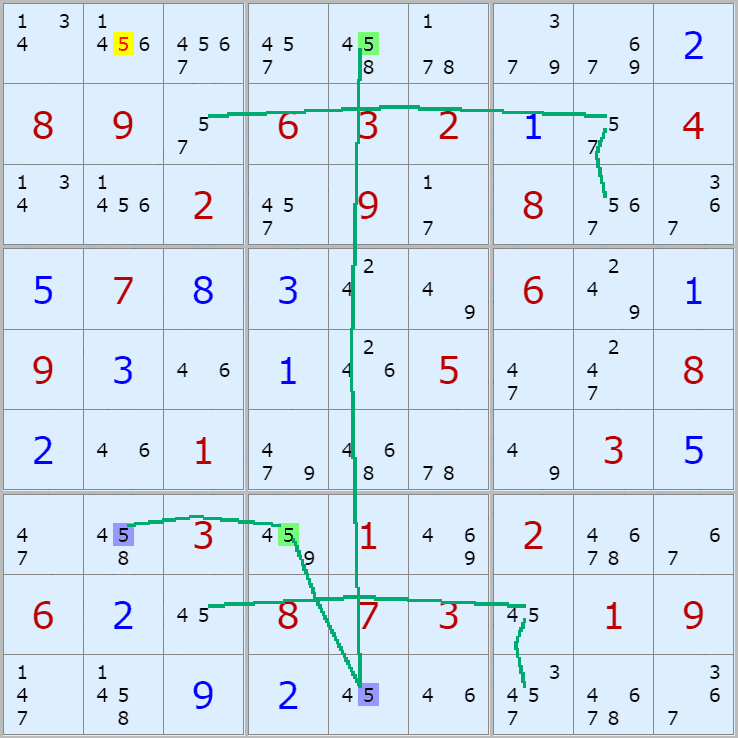
(2,8)칸이 3이 아니라면
(2,6) On > (9,6) Off > (9,7) On > (7,9) Off > 끝점 (1,9)이 On 이 되며
(2,8)과 마주보는 칸 안에 있는
(1,8)칸에 있는 후보숫자 3을 1개 제거할 수 있다.
경로는 2개의 갯수가 있다.
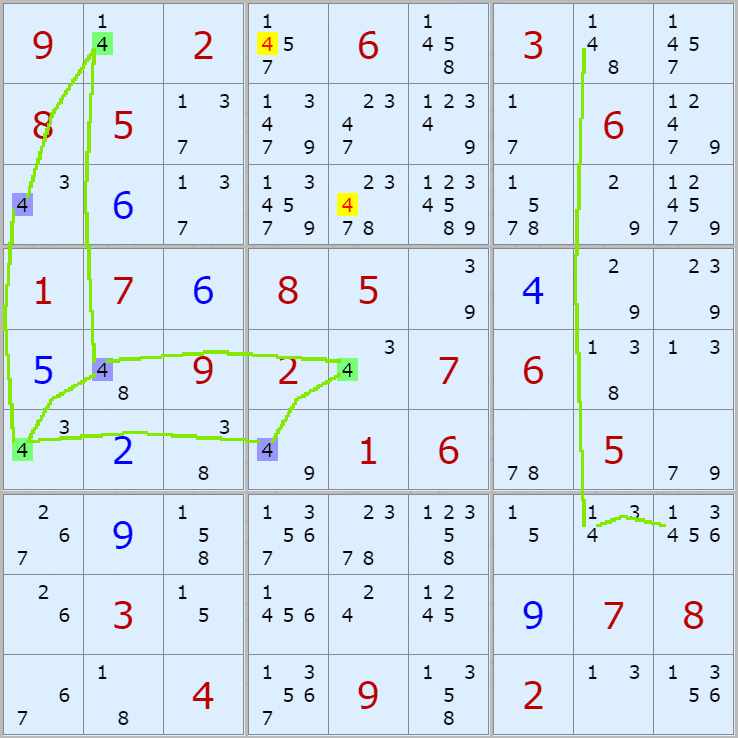
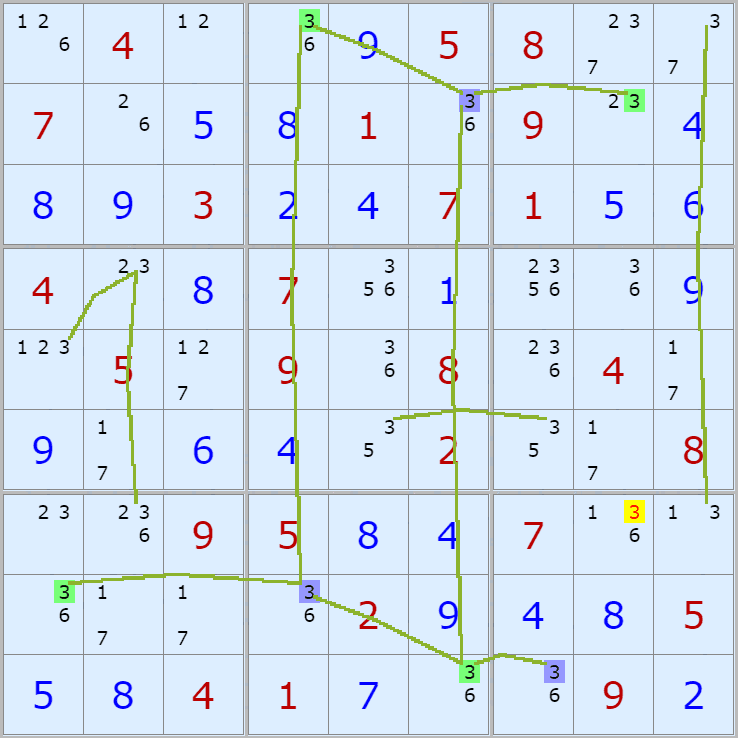
003.
(7,7)칸이 4가 아니라면
(5,7) On > (5,3) Off > 끝점 (9,3) On 이 되며
(7,7)과 마주보는 칸 안에 있는
(6,2) 및 (9,8)칸에 있는 후보숫자 4를 2개 제거할 수 있다.
경로는 2개의 갯수가 있다.

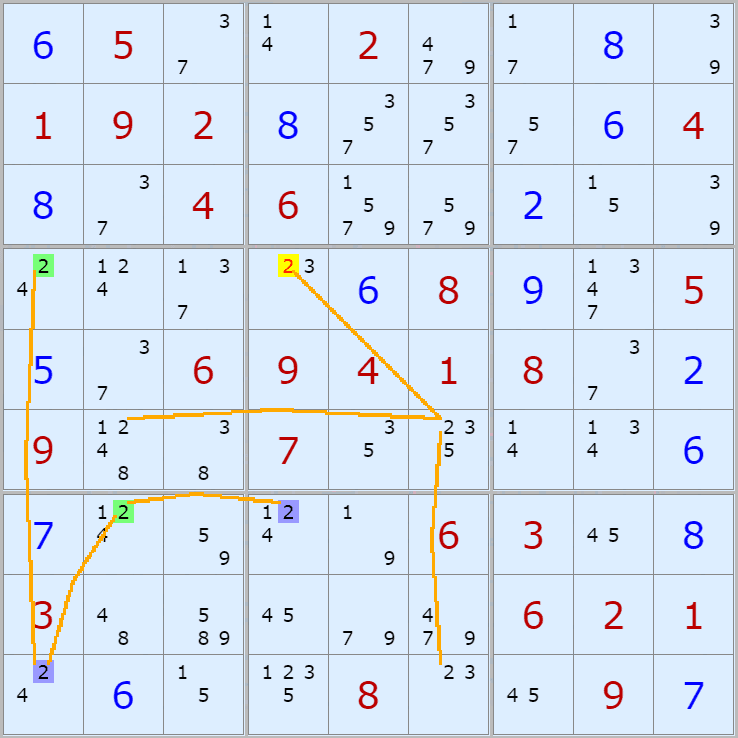
(8,7)칸이 2가 아니라면
(8,4) On > (1,4) Off > (2,5) On > (2,2) Off > (3,1) On > (9,1) Off > 끝점 (9,7) On 이 되며
(8,7)과 마주보는 칸 안에 있는
(7,7) 칸에 있는 후보숫자 2를 1개 제거할 수 있다.
경로는 복수의 갯수가 있다.



































Andoku 스도쿠 3 - 강력 스도쿠 추천 앱
스도쿠에 빠져든지 2달이 막 지나는 지금 현재까지 10가지 정도의 앱을 광고 보면서 써보고 2개의 앱을 유료결제로 사용하다가 전문가 난이도인데 뭔가 맥없이 풀리는 것 때문에 조금 스도쿠의
inoks.tistory.com
11월 8일 추가 > 싱글체인 움짤 예제 23개