움짤로 익히는 스도쿠 16. 버그(Bi-Value Universal Grave)

 이번 글에서는 스도쿠를 풀다가 종반에 칸의 갯수에 상관없이 한 칸만 3개의 후보숫자가 있고 나머지 모든 칸이 이중위치, 즉 2개의 후보숫자만 남아 있는 경우에 특별한 공식을 쓰지 않고 쉽게 직관적으로 트리거가 되는 후보숫자를 확정할 수 있는 BUG라는 공식에 대해 알아 보도록 하겠다. 
 
 Bi-Value Universal Grave(보편적인 이중위치 값 무덤) 줄여서 BUG라고 칭하는데, 기술의 성질상 BUG를 쓸 상황이 되었을 경우,
 
 유일하게 3개의 후보숫자가 남은 칸의 후보숫자의 결과에에 따라
 
 답이 2개가 되는 치명적인 모순이 발생하는 경우가 생길 수 있다.
 
 이런 이중값의 모순을 제거하는 개념이라고 보면 되겠다. 
 
역시 말로 스도쿠를 설명하기는 어렵다. 
 
 우선 공식을 적용하는 방법을 움짤로 보고 원리를 설명하도록 하겠다. 

 
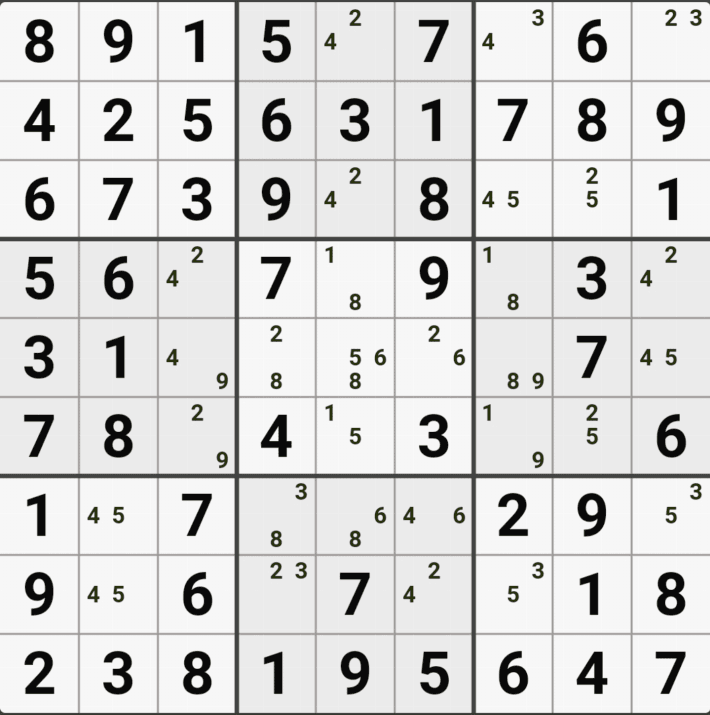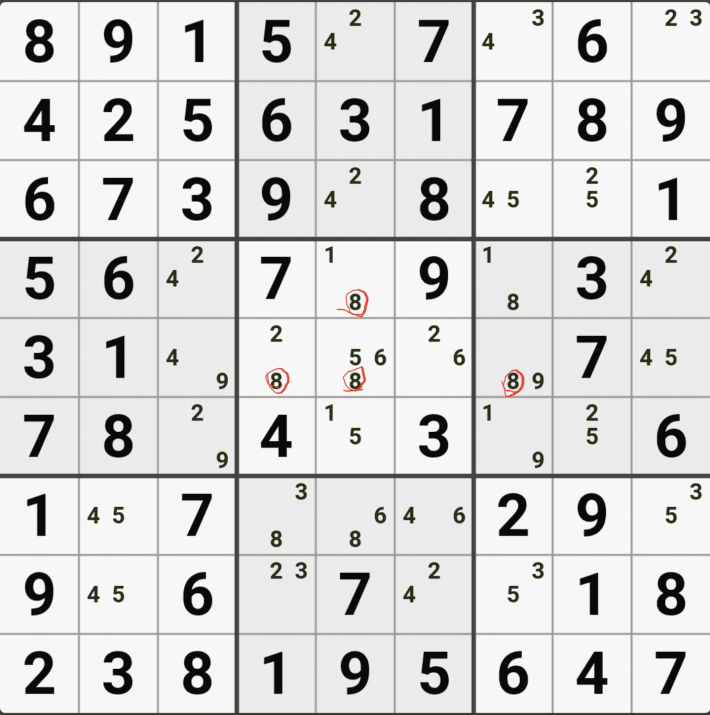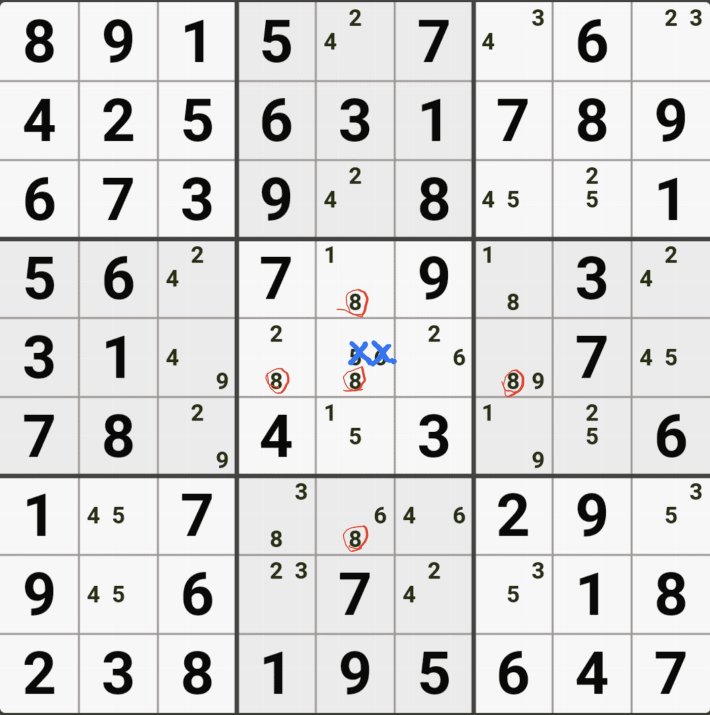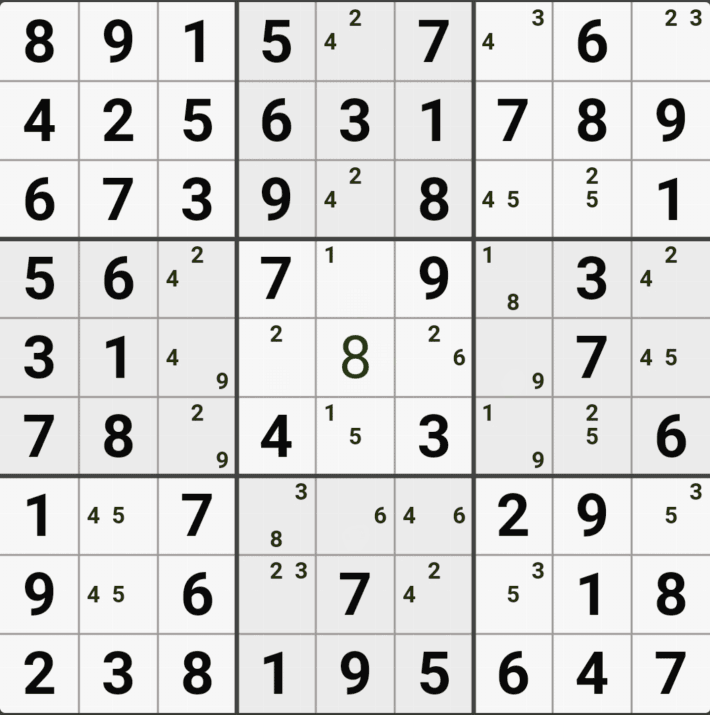
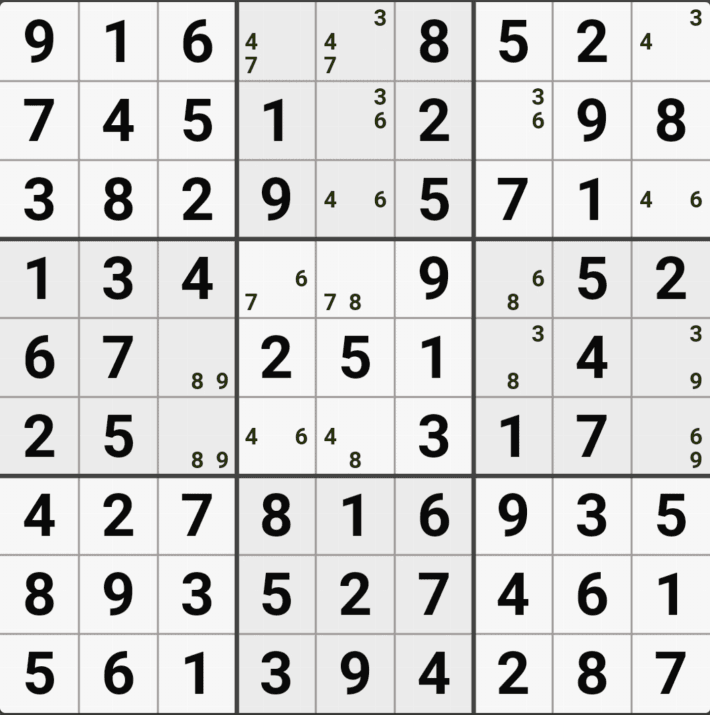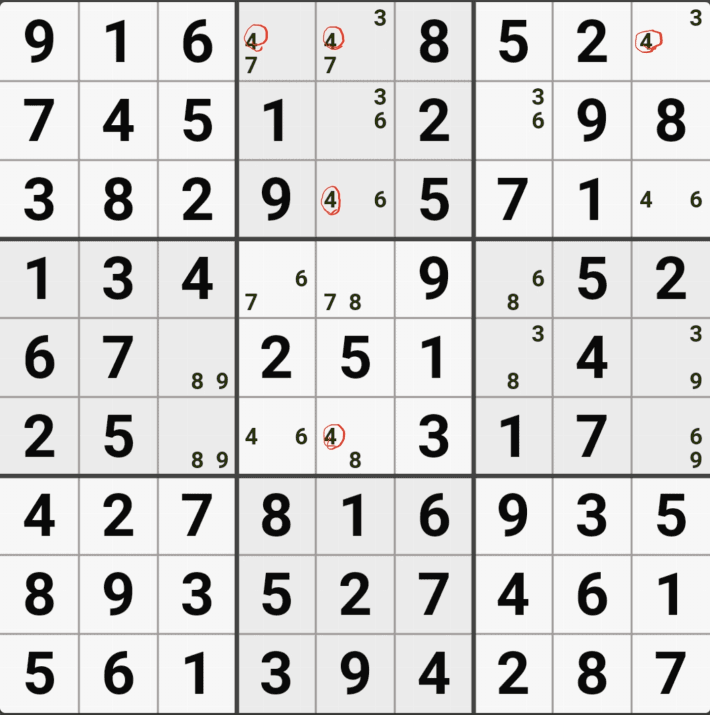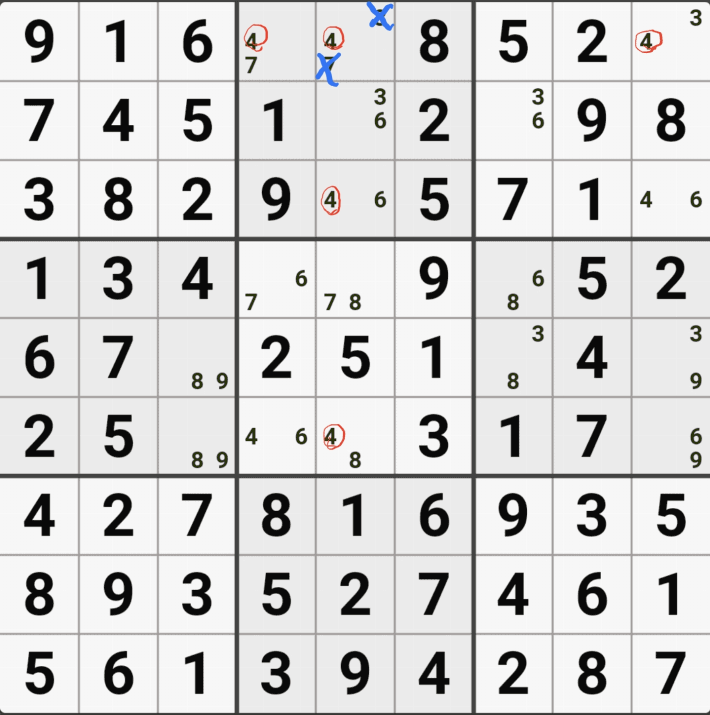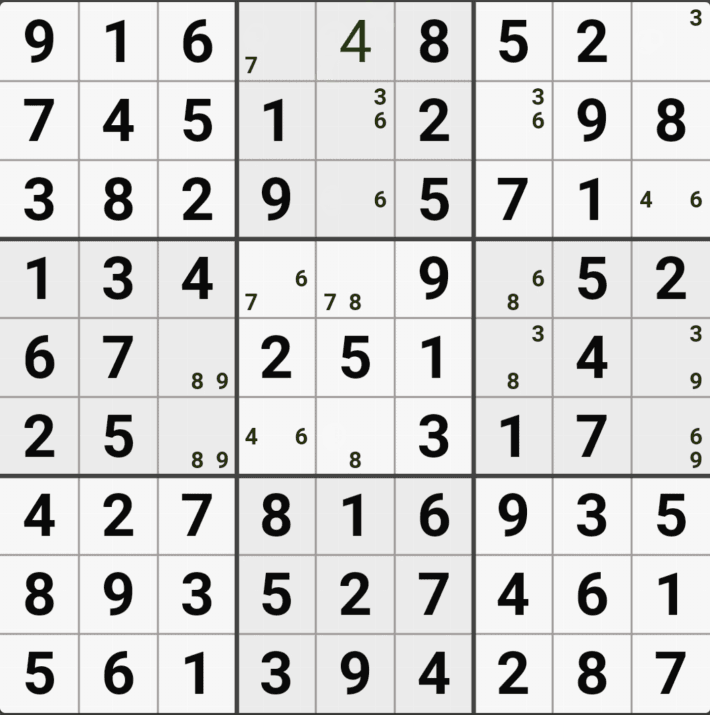
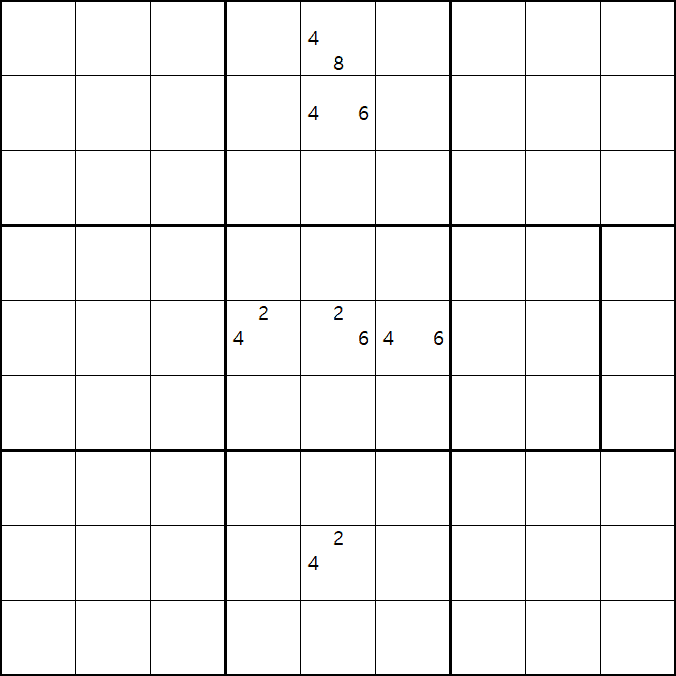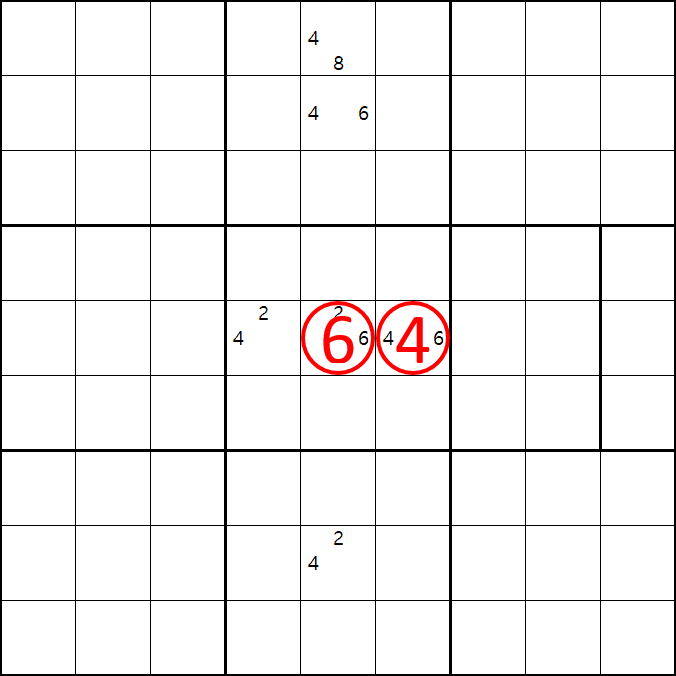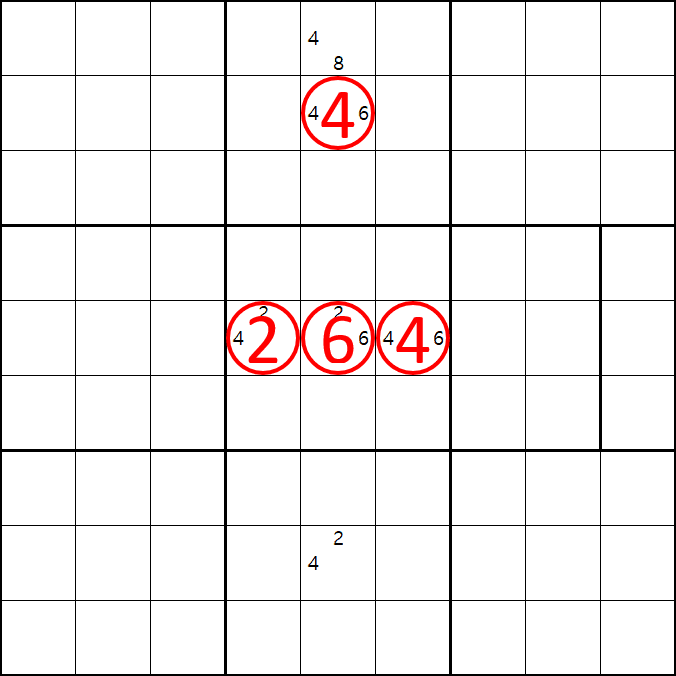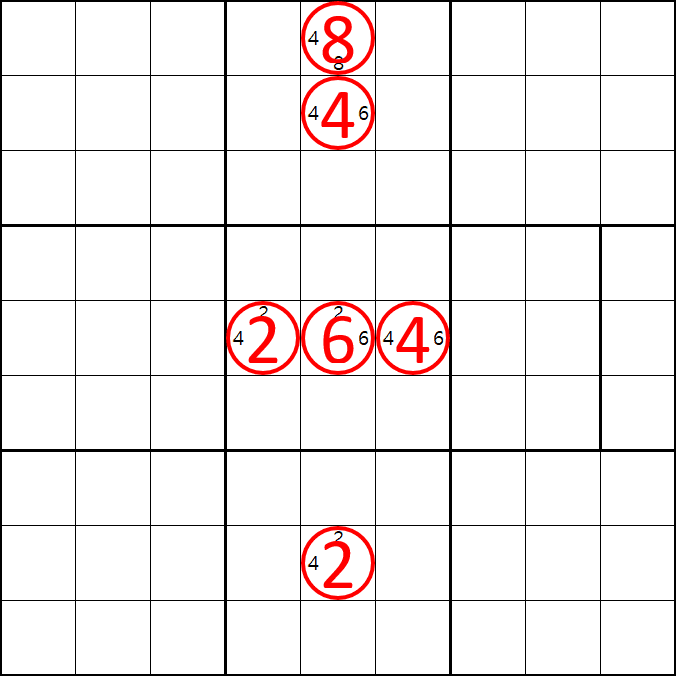
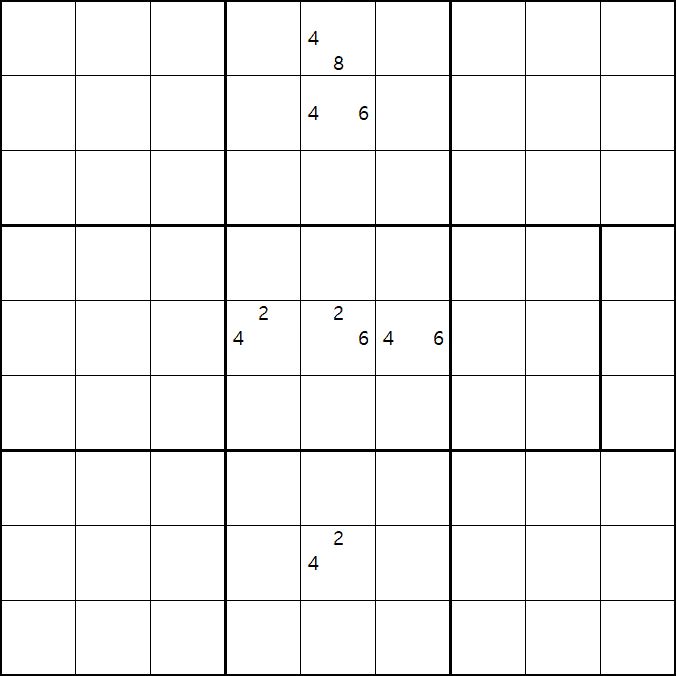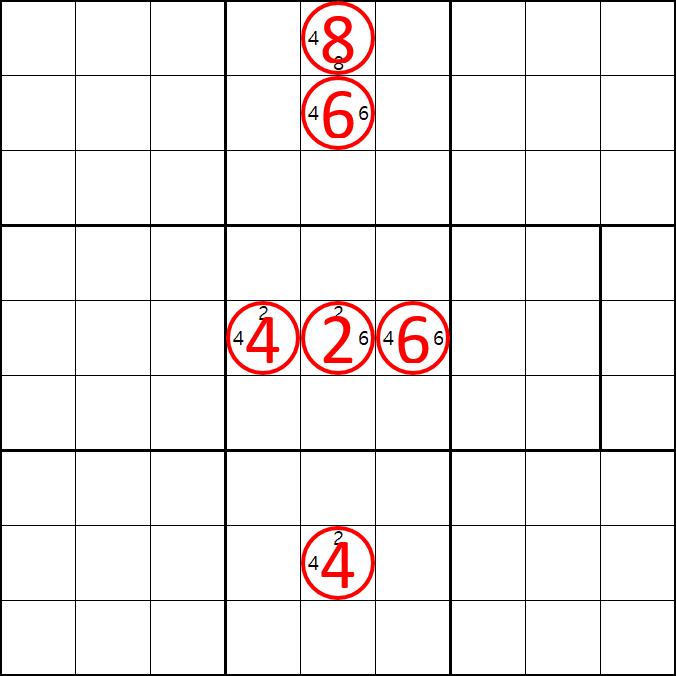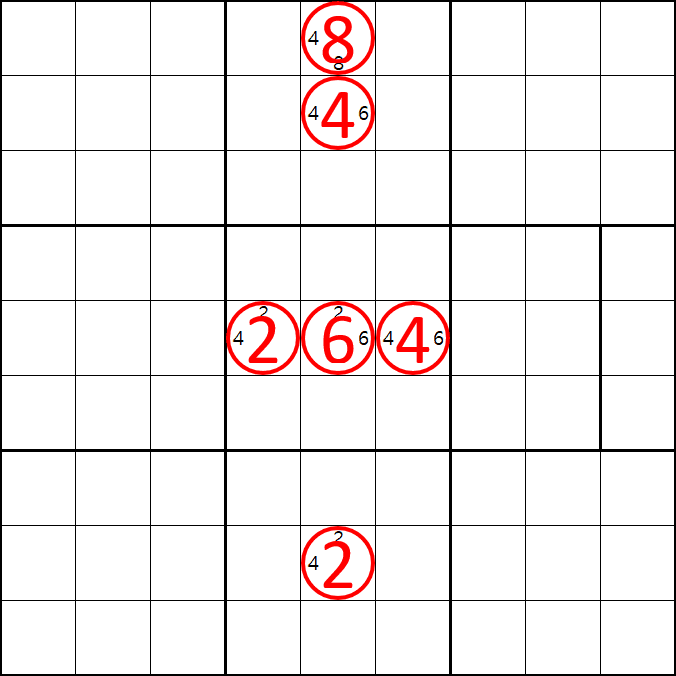
위의 움짤과 같이 4/8[A5], 4/6[B5], 2/4[E4], 2/4/6[E5], 4/6[E6], 2/4[H5]로 남아 있을 때, 

2/4/6[E5]의 해가 2 또는 6이 된다면 답이 2개가 되는

스도쿠의 치명적인 모순이 발생하게 되어 
2/6[E5] 을 제거하여야 한다. 즉 4[E5]가 해가 된다.
 
고 설명하면 어려울 거 같고, E행 3개 - 5열 4개 존재하는(가장 많은 숫자가 있는) 후보숫자 4가 해가 된다. 고 기억하면 편하겠다. 
 
만약에 후보숫자 4외의 후보숫자인 2/6[E5] 둘 중의 하나가 해가 되는 상황으로 위의 결과를 증명해 보겠다. 
 
증명 1. 2[E5]인 경우
 

 
2[E5] 가 된다면
4[E4], 6[E6], 8[A5], 6[B5], 4[H5]
가 된다. 
 
증명 2. 6[E5]인 경우

6[E5] 가 된다면
2[E4], 4[E6], 8[A5], 4[B5], 2[H5]
가 된다. 
 
증명3.
증명1. 의 결과
 
2[E5] 가 된다면
4[E4], 6[E6], 8[A5], 6[B5], 4[H5]
가 된다.' 와
 
증명2. 의 결과
6[E5] 가 된다면
2[E4], 4[E6], 8[A5], 4[B5], 2[H5]
가 된다.' 를 보면
 
E행에서는
2[E5], 4[E4], 6[E6]
6[E5], 2[E4], 4[E6]
과 같이 2개의 답이 존재하게 되고, 
 
5열에서는 8[A5]를 제외한
6[B5], 6[E5], 4[H5]
4[B5], 6[E5], 2[H5]
과 같이 2개의 답이 존재하게 된다
 
따라서 81개의 칸 중에 모든 숫자는 1번씩 들어 간다는 스도쿠 규칙에 반하기 때문에 후보숫자 2와 6은 해가 될 수 없다.'고 쓰면 머리에 잘 들어오지 않을 것이다. 증명1.과 증명 2의 결과만 움짤로 엮었다. 
 

 
 위의 움짤과 같이 2개의 답이 발생하는 치명적인 모순이 발생하는 경우는 2개의 후보숫자를 갖는 이중 위치칸을 확장해도 '3개의 후보숫자가 남는 칸이 1칸이 되는 상황이면 언제나 적용된다.' 그래서 '3개의 후보숫자가 속한 행 또는 열과 박스에 후보숫자가 3개인 숫자가 해가 된다.'고 기억하면 되겠다.'라고 쓰지만 아직 개념이 자리 잡히지 않는 스도커가 있을 것이다. 
 
 아래의 실전 예제 움짤을 보고 BUG에 대해 정확히 이해해 보자!! 다른 공식으로 재차 증명해 보겠다. 
 
실전예제1. BUG 사용

 
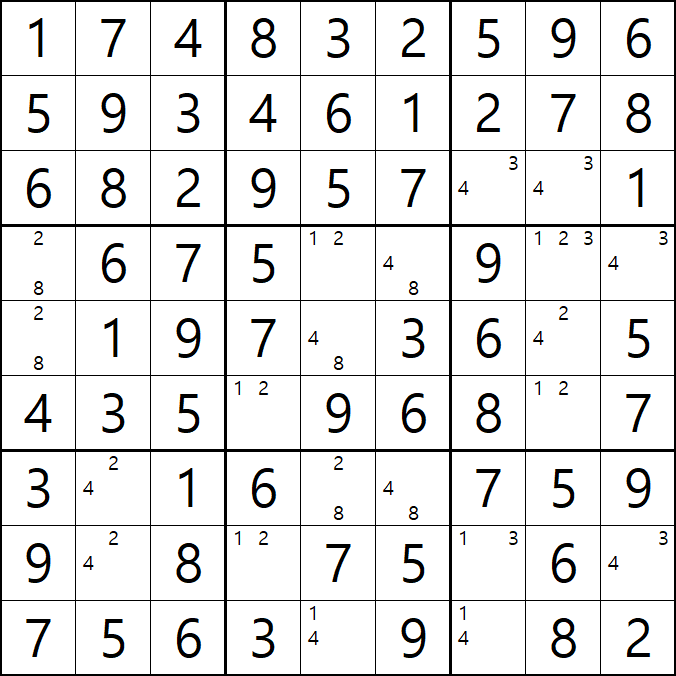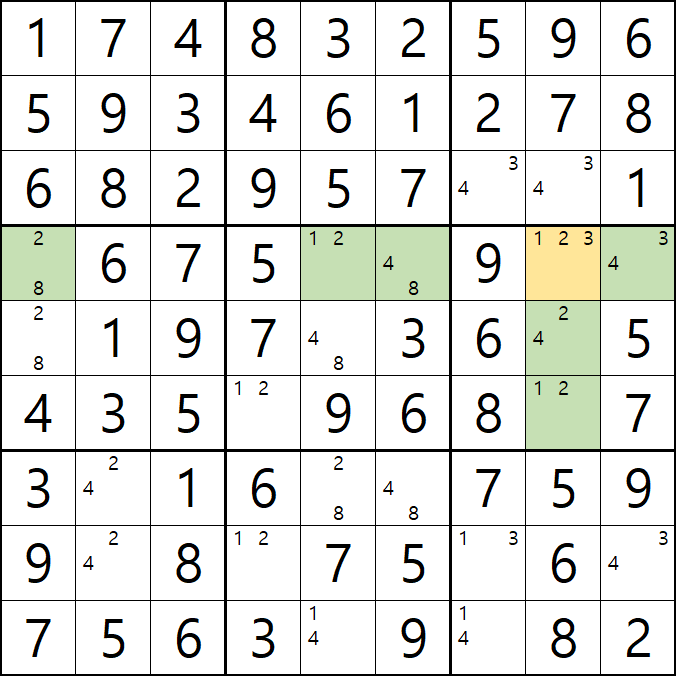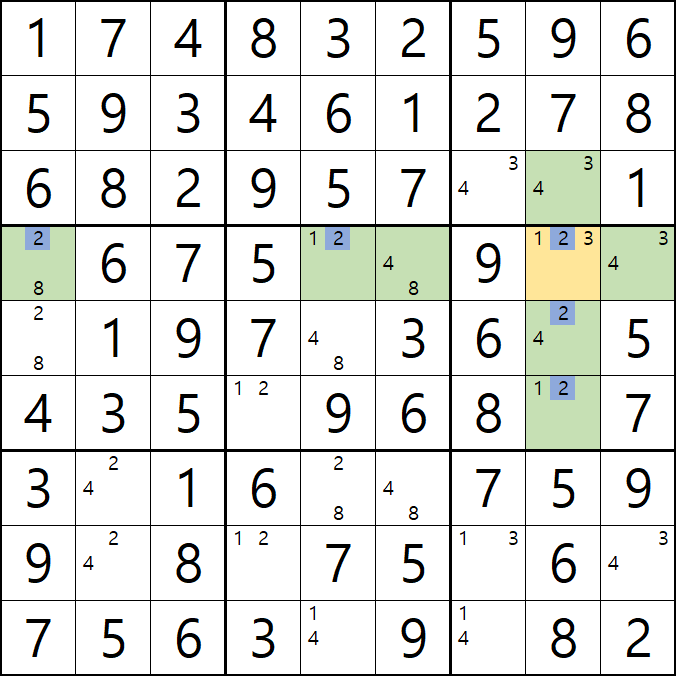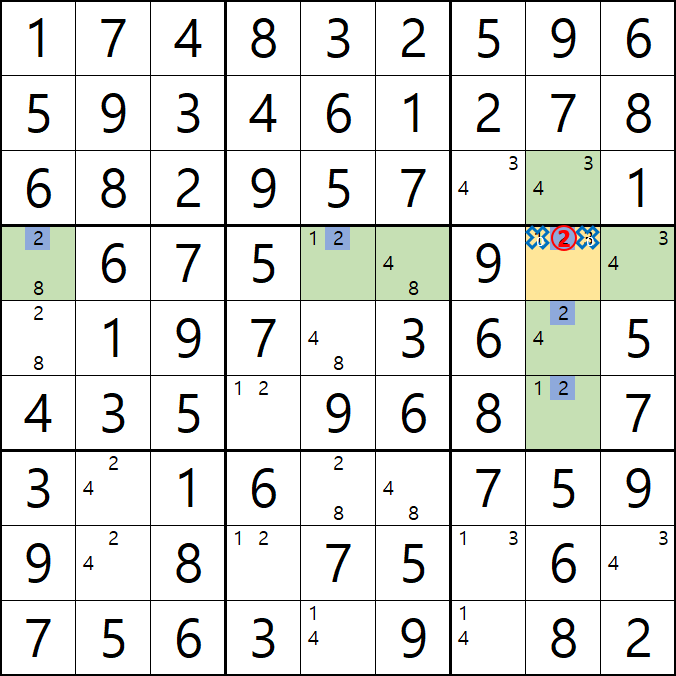
위의 움짤과 같이
1/2/3[D8]에 치명적인 모순을 발생할 수 있는 후보숫자 1/3을 제거하여야 한다. 
즉, 2[D8]이 해가 된다.'가 어렵다면~
 
아래와 같이 D행에 2가 3개, 8열에 2가 3개 있으므로 2[D8]이 해가 된다.로 기억하자....
 
위의 실전예제1.'을 XY체인으로 증명해 보겠다. 
 
실전예제2. XY체인으로 실전예제1. BUG 증명

 
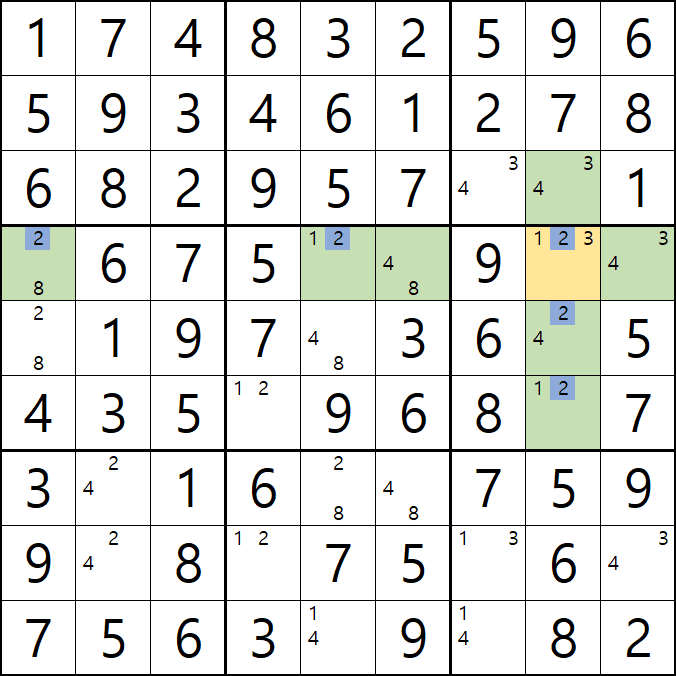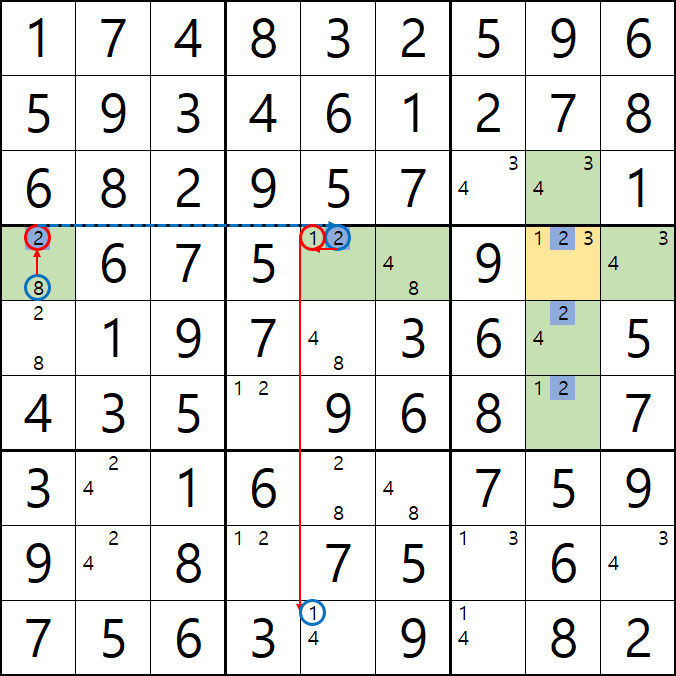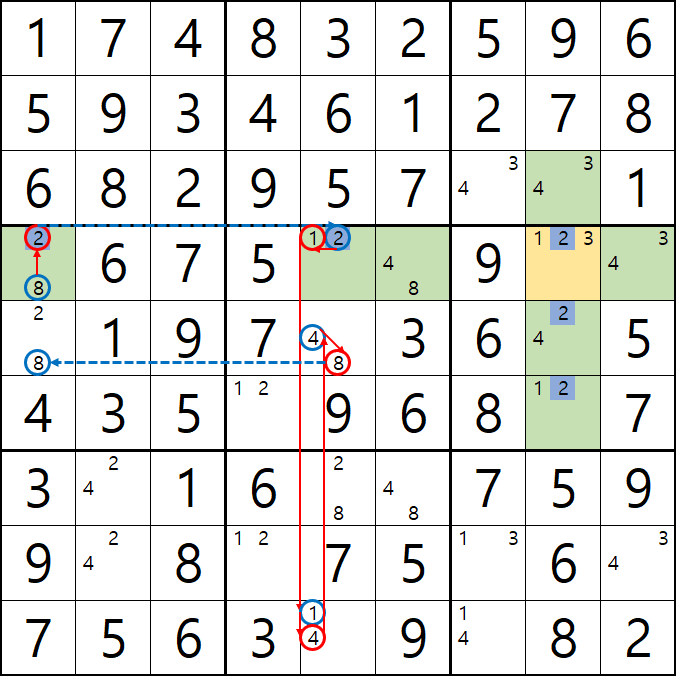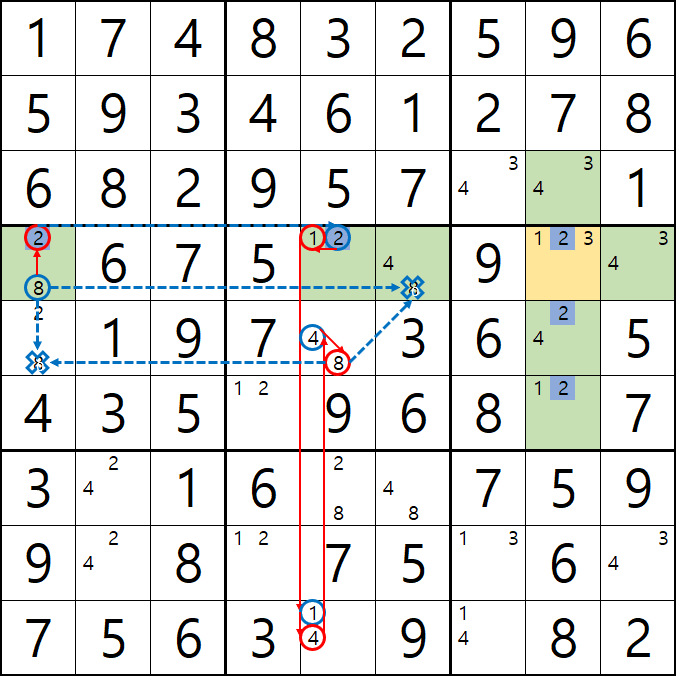
-8[D1] +2[D1] -2[D5] +1[D5] -1[I5] +4[I5] -4[E5] +8[E5] + {-8[E1] & -8[D6]}이 되어
D행에 -8[D1]과 -8[E1] OFF가 동시에 2개, 
1열에 -8[D1]과 -8[D6] OFF가 동시에 2개 발생하는 모순이 발생하게 된다. 
 
이런 모순을 제거 하기 위해 모순을 발생시키는 -8[E1] & -8[D6]을 제거 하여야 한다. 
 
그 후 아래 움짤과 같이 추가로 확정숫자를 찾아 가다 보면 2[D8]가 해가 되는 것을 알 수 있다. 

 
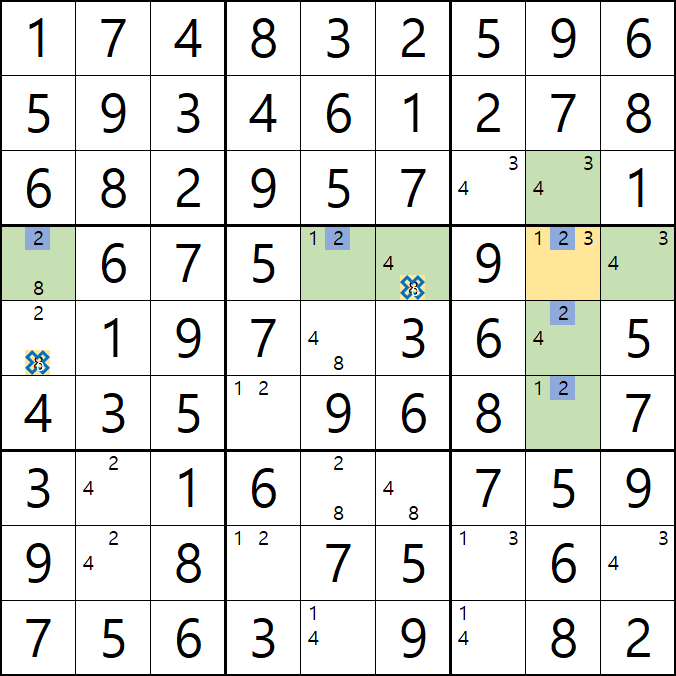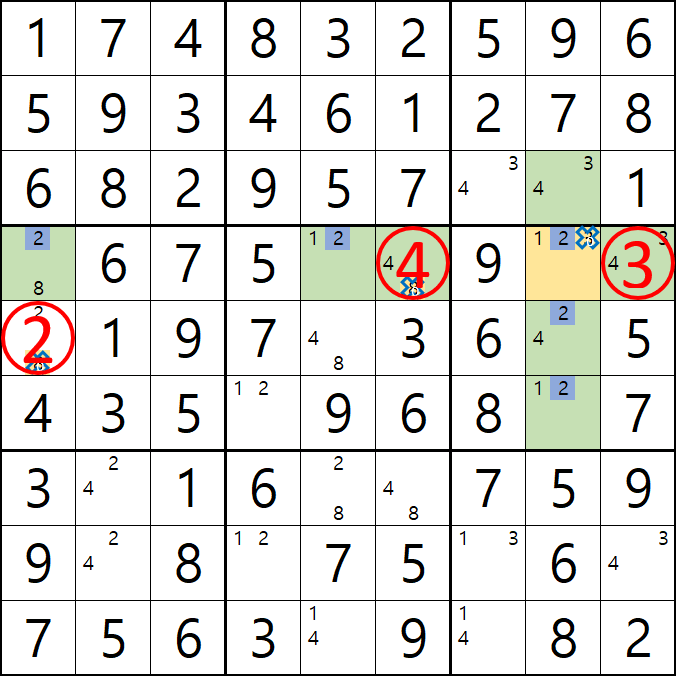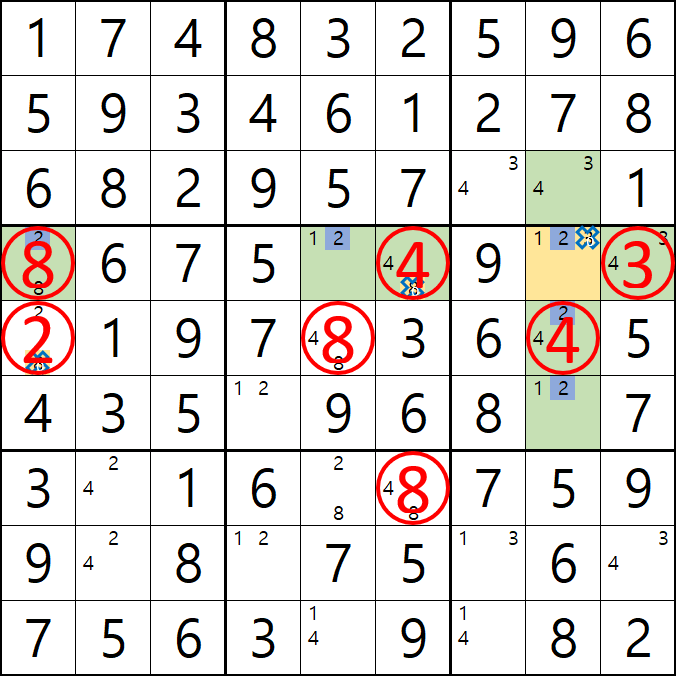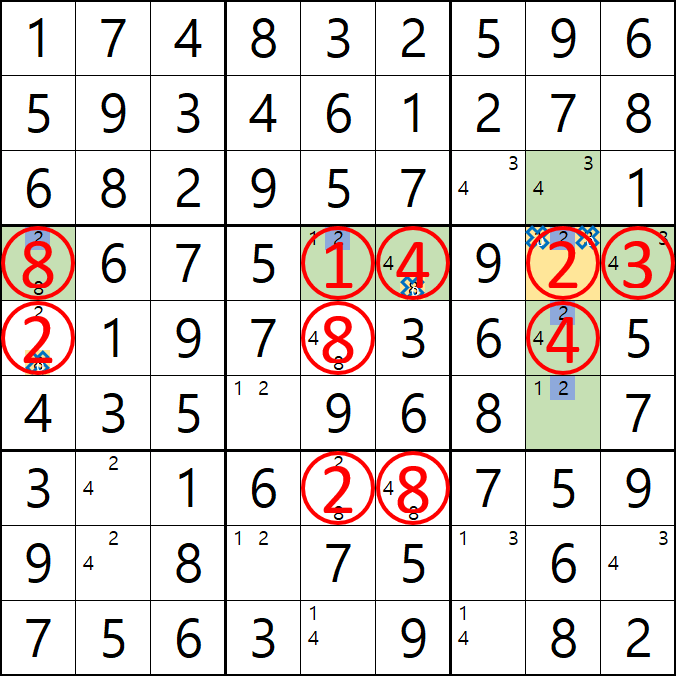
자 BUG vs XY-CHAIN 둘 중 어떤 길을 가고 싶은가? BUG 개념은 예제가 많지는 않지만 많이 보고 이해하거나 통으로 외우자!!)
 
 잘 이해했을거라 믿지만... BUG 사례가 자주 나타나지는 않고, 모든 것은 반복이 중요해서, 추가로 6개의 예제를 찾아서 움짤로 만들어 올린다!! 설명은 따로 하지 않겠다~