움짤로 익히는 스도쿠 6. X윙, 소드피쉬, 젤리피쉬

 이번 글에서는 형제격인 스도쿠 공식 X윙(X-Wing), 소드피쉬(Sword Fish), 젤리피쉬(Jelly Fish)에 대해 알아 보도록 하겠다. 이 3개의 공식은 X체인 공식에서 모양이 정형화 되어 수학공식처럼 이름을 붙인 것인데 명칭의 유래는 알 수 없다. 기본형태는 아래와 같다. X윙은 2 x 2의 사각형, 소드피쉬는 3 x 3 사각형, 젤리피쉬는 4 x 사각형의 모양을 갖는다. 

 

 예전에 '스도쿠 솔브'라는 사이트에서 예제 400개를 조사했을 때, X윙은 4판 중에 3판, 소드 피쉬는 4판 중에 1판, 젤리 피쉬는 발견하지 못했었다. 즉 X윙 출현빈도는 75%(기본 공식으로 익혀야 한다.), 소드 피쉬 25%(찾을 수 있을 정도로는 공식을 익혀야 한다.), 젤리 피쉬 N/A (찾는 방법만 일단 알고 있자!!)

 

 

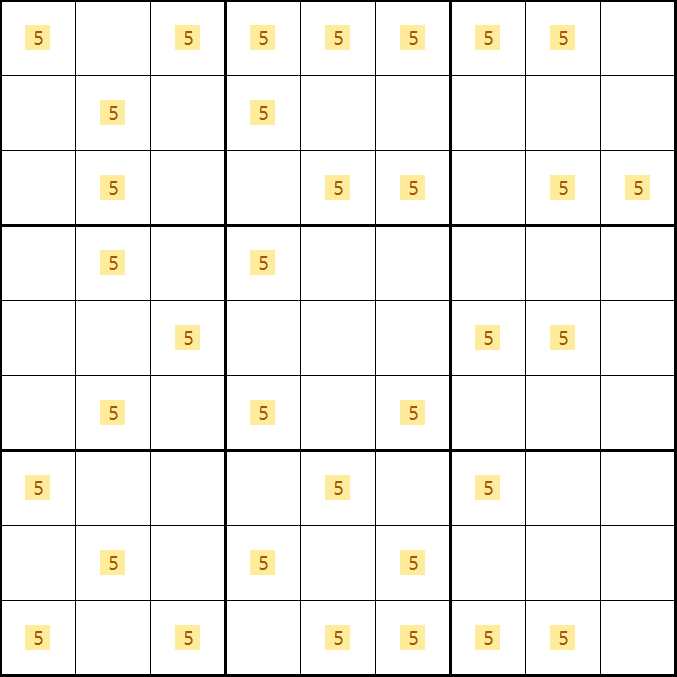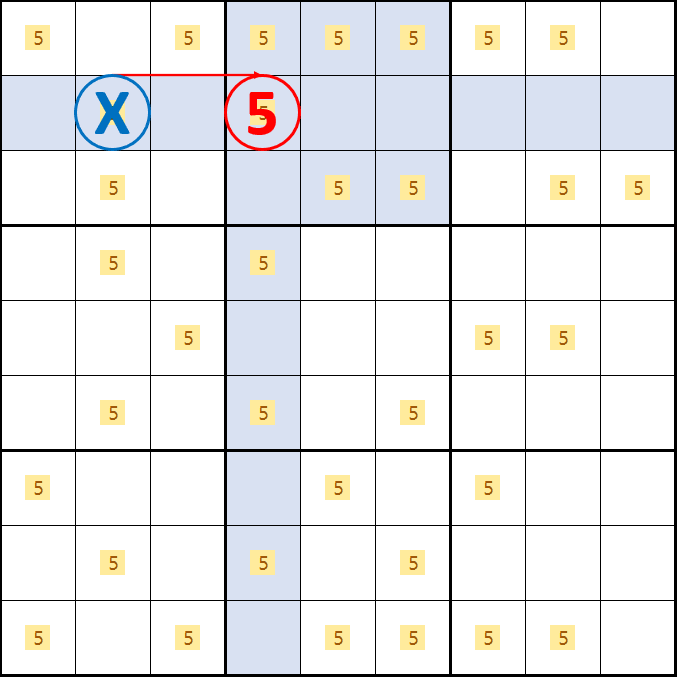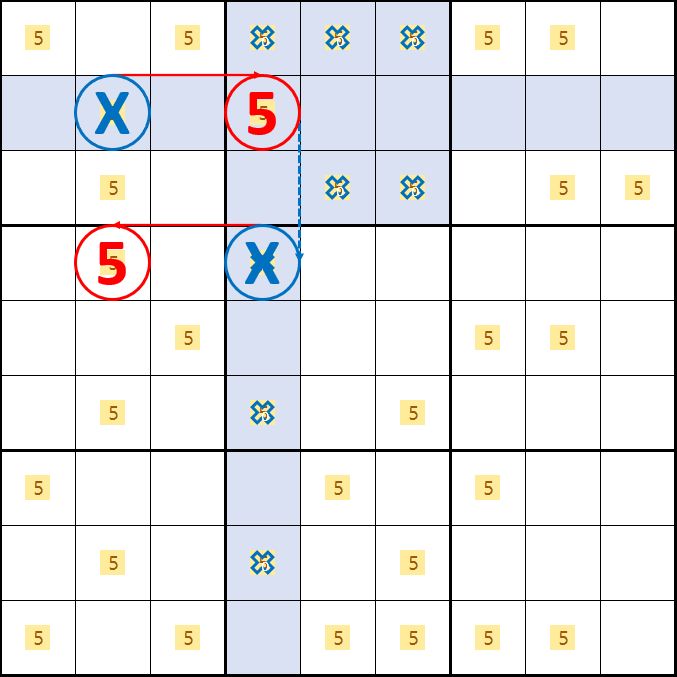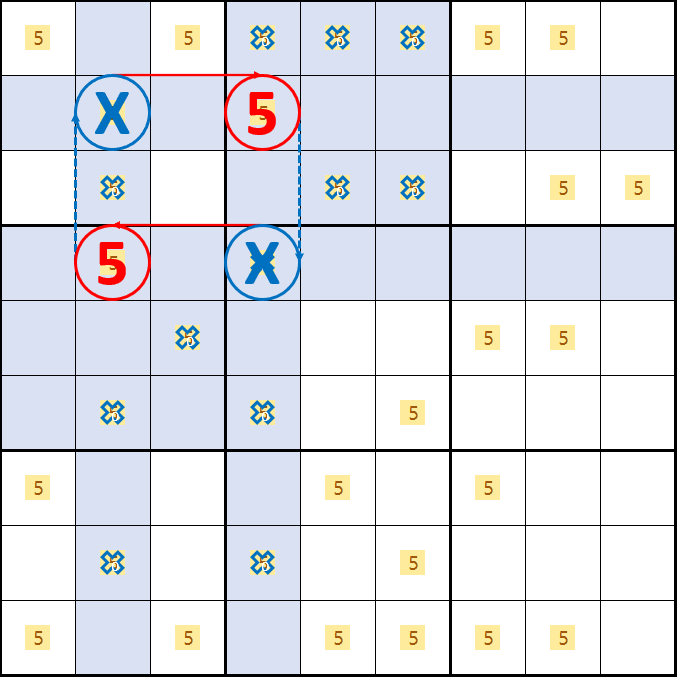
 X윙의 경우는 움짤과 같이 2 x 2 사각형 안에 무조건 대각선 방향으로 후보숫자 X가 4개 들어가는 1개의 경우의 수만 존재하는 반면에 

 

 소드피쉬는 위의 움짤 3 x 3 사각형 안에 333 기본형 외에 332 > 322 > 222 등으로 변형되어 최소 6개~최대 9개가 들어가며 6개의 경우의 수가 존재하며 

 

 젤리피쉬는 4 x 4 사각형 안에 4444 기본형 외에 4443 > 4433 > 4333 > 4332 > 4322 > 4222> 3333 > 3332 > 3322 > 3222 > 2222 등의 형태로 최소 8개~16개까지의 후보숫자가 들어가는 24개의 경우의 수가 존재한다.  

 

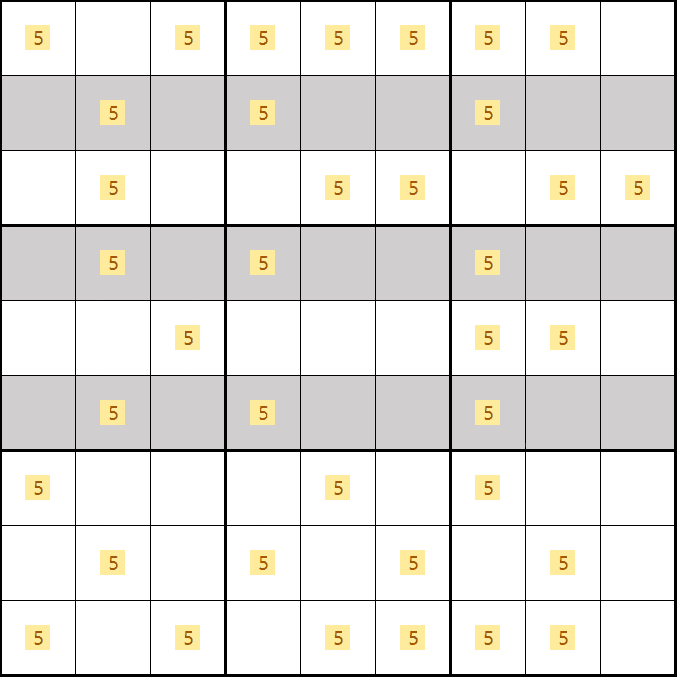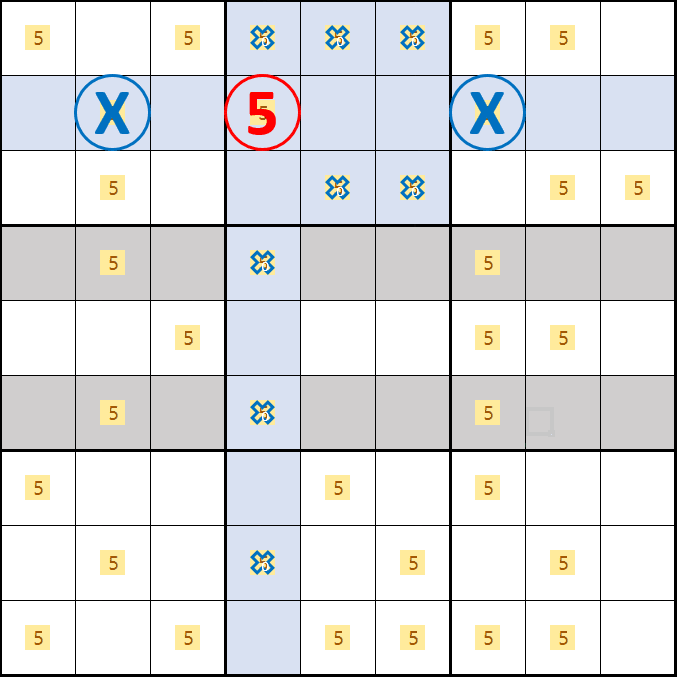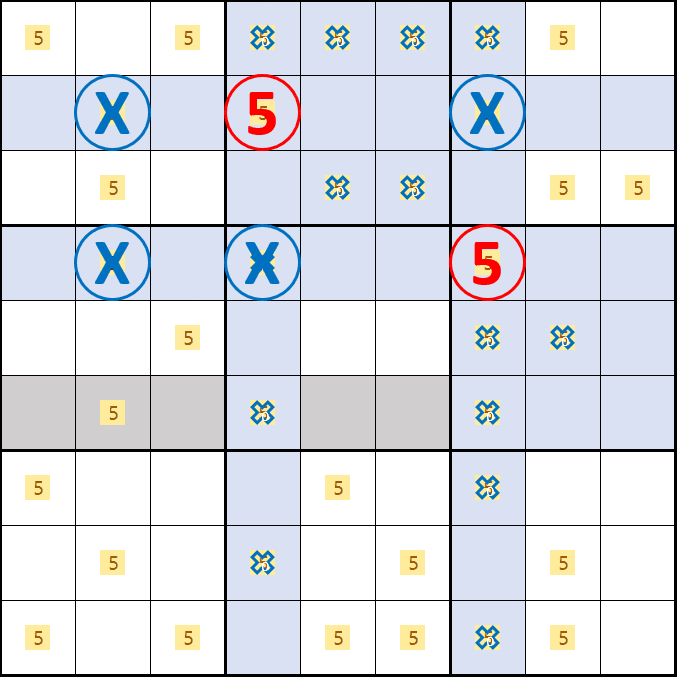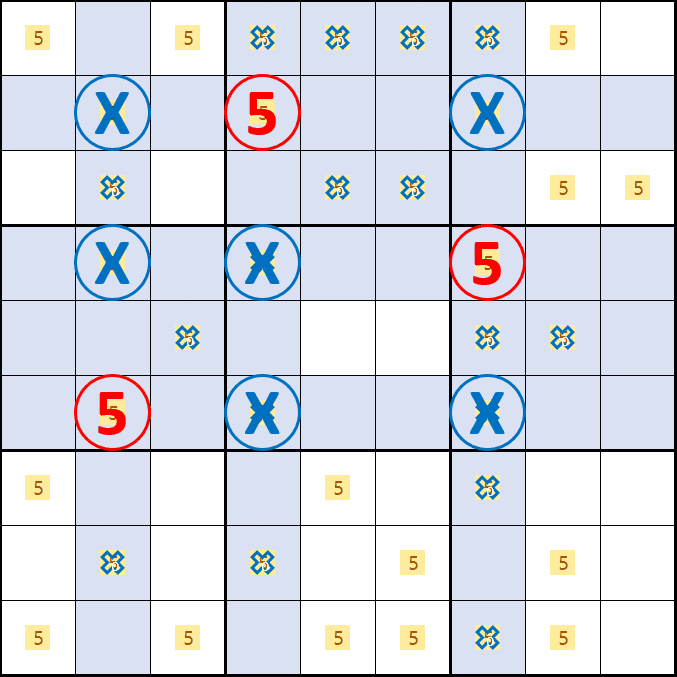
 모든 경우의 수에 대한 이야기를 하면 좋겠지만, 모든 칸에 후보숫자 5가 들어가는 상황에서 위의 공식들이 작동하는 방법을 알아 보도록 하겠다. 또한 모양도 변형이 많아서 우선 기본 개념을 익히고 실전 또는 예제로 다른 패턴을 익혀야 한다. 특히 X윙은 딱 보면 탁~ 하고 알 수 있을 정도로 많이 봐야한다.

 

1. X윙(X-Wing)

 

 X윙은 아래 움짤과 같이 (스마트폰이라면 방향을 90도> 180도 > 270도로 돌려서도 보자. 스도쿠의 모든 예제는 4개의 각도로 보는 것을 권한다.)

 

 1. 행 또는 열에 대한 후보숫자 X의 잠긴 페어가 쌍을 이룰 때 

 2. 잠긴 방향의 직각 방향에 있는 다른 후보숫자 X를 지울 수 있다

 

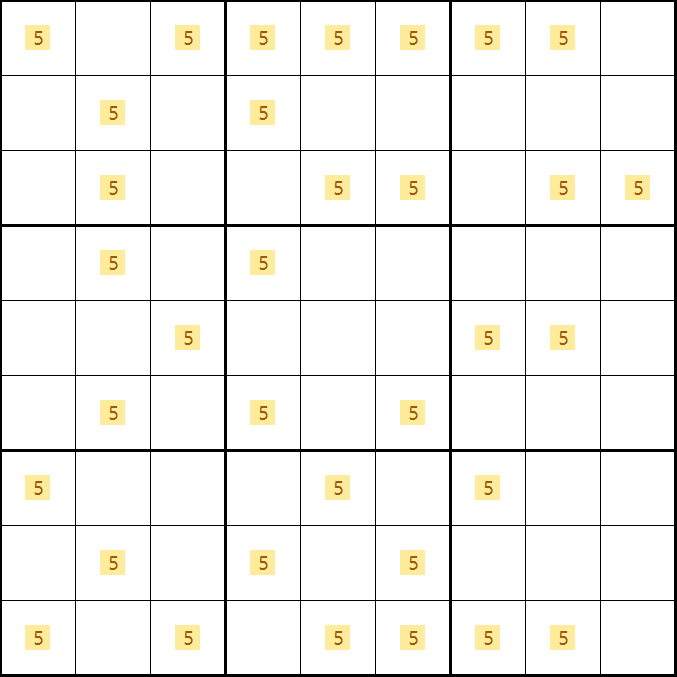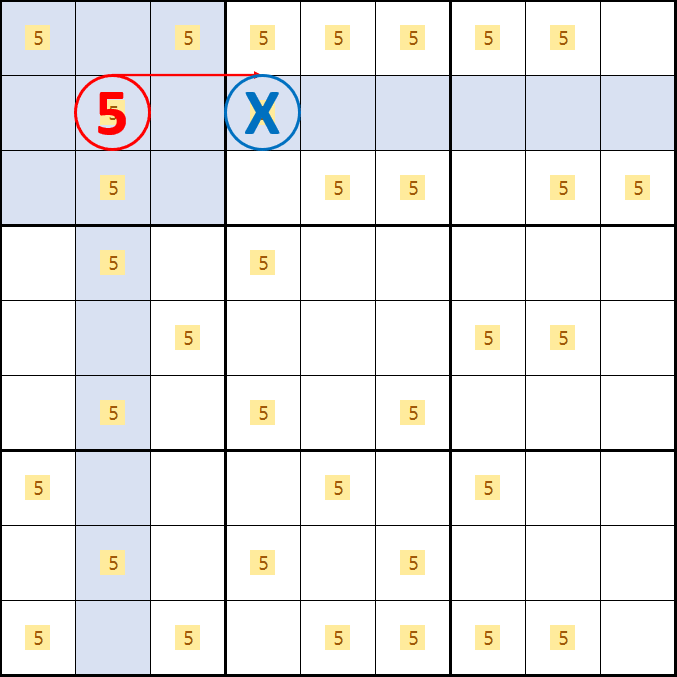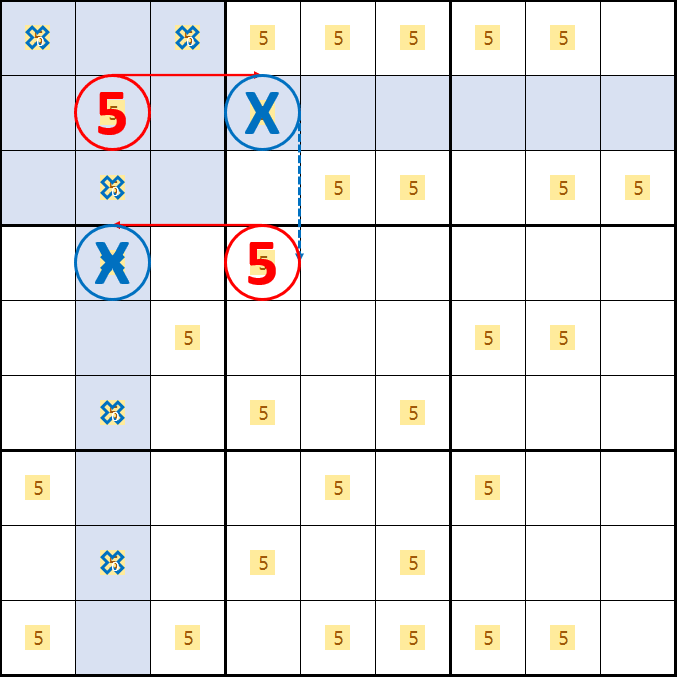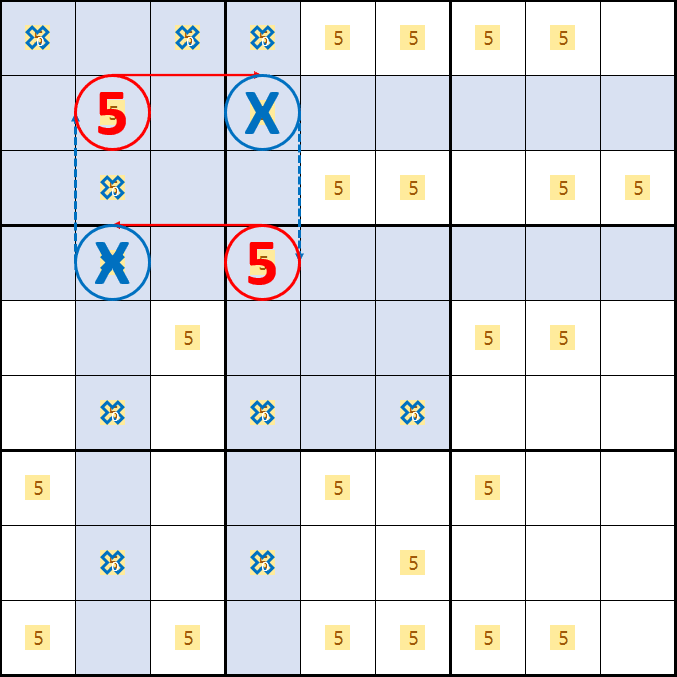
 위의 X윙 다이아그램 움짤을 읽는 방법은 

 

 B2칸이 5가 아니라면

 B4칸이 5가 되고

 D4칸이 5가 아니고

 D2칸이 5가 되어 

 2열과 4열의 후보숫자 5를 제거할 수 있다. 

 

 로 리딩이 되는데 

 

 조건을 바꾸더라도 같은 값이 나오지만 움짤로 2가지 경우의 수를 증명해 보면 아래와 같다. 

 

X윙 증명1. D2가 5가 아니라면

 

B4가 5가 되어 박스 2 및 4열의 후보숫자 5를 제거할 수 있고

D2가 5가 되어 박스 4 및 2열의 후보숫자 5를 제거할 수 있다. 

 

X윙 증명2. D2가 5라면

 

 

B4가 5라면 박스 1 및 2열의 후보숫자 5를 제거할 수 있고

D4가 5가 되어 박스 4 및 4열의 후보숫자 5를 제거할 수 있다. 

 

X윙 증명 3. 위의 X윙증명1과 X윙 증명2에서 교집합 부분이 되는 2열과 4열은 어떠한 경우라도 제거될 수 있다. 

 

이를 시각적으로 볼 수 있도록 증명1의 결과와 증명2의 결과를 합쳐서 움짤로 만들면 아래와 같고, 2열과 4열에서 제거되는 후보숫자만 변동이 없고, 1,3,5,6열의 후보숫자 5는 경우에 따라 제거 되기도 하고 안되는 것을 알 수 있다. 

 

 위의 X윙 개념을 심화해서 익힐 수 있도록 '스도쿠 솔브'라는 사이트에서 캡쳐해 온 X윙 다이아그램 예제 296개를 움짤로 만들어 올린다. 처음 접해서 알지 못하더라도 자꾸 보면 알게 되고 익숙해 진다. '보고~ 또 보자~' 

 

 

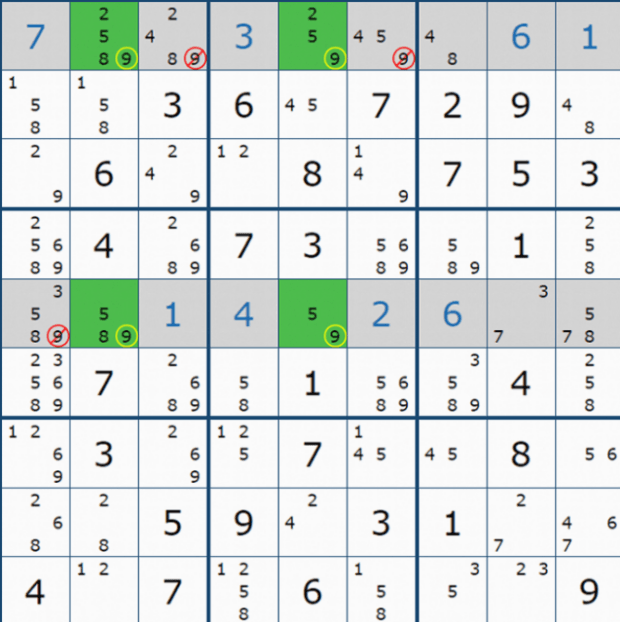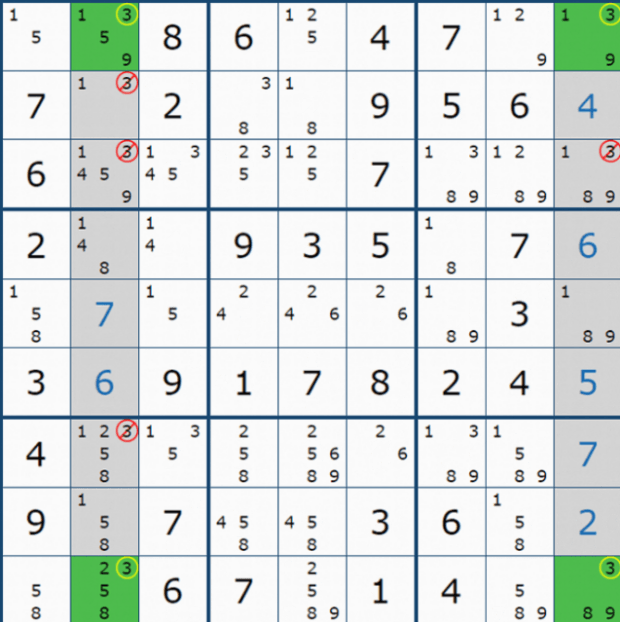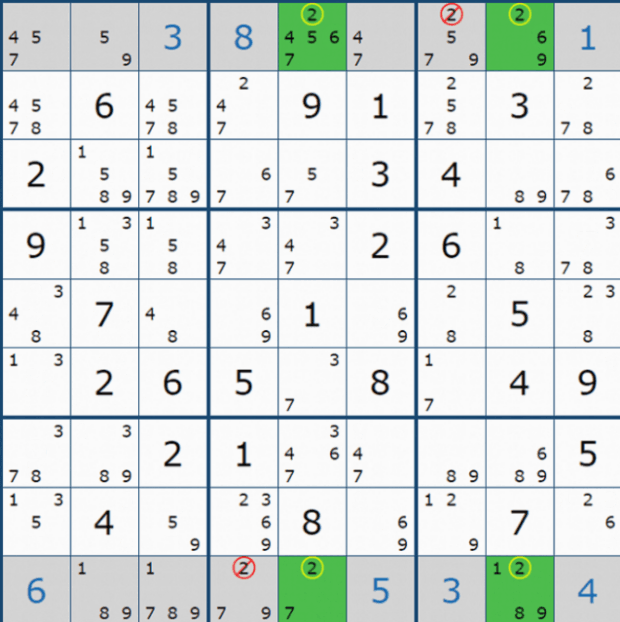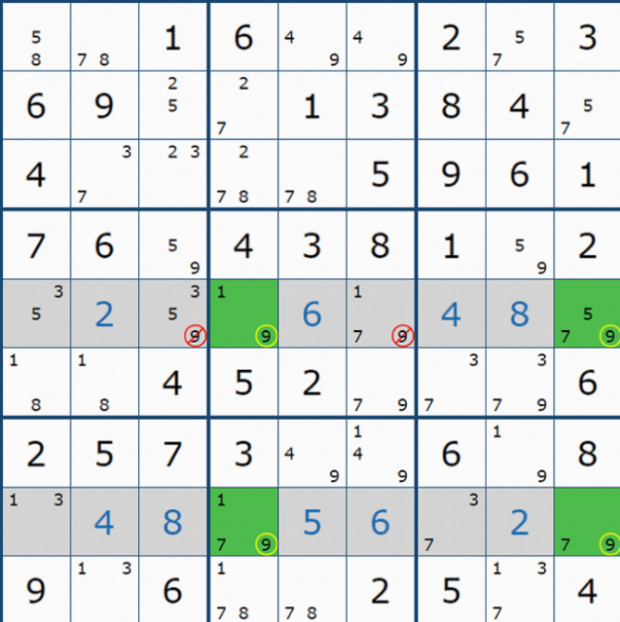
 그림으로 쭉 올리려고 했는데, 용량의 문제도 생기고 대부분 잘 보지 않고 넘어가서 움짤로 만들었다. 이렇게 나도 정성 들여 올리는 이유는 X윙은 매우 빈번해서 중요한 역할을 하는 공식이기 때문이다. 보자~. 그렇지만 위의 움짤을 찬찬히 보고 싶은 이들도 있을 것이다. 

 

 아래 링크로 가서 실컷 보자~

 

스도쿠 기본공식 패턴 모음 3/엑스윙(X-Wing)

스도쿠 기본공식 패턴 모음 3/엑스윙(X-Wing)

 

2. 소드 피쉬(Sword Fish)

 

 소드 피쉬는 스워드 피쉬라고도 불리며 

 아래의 움짤과 같이

 X윙 2 x 2에서 개념이 확장된 3 x 3 공식으로  

 

 1. 행 또는 열에 대한 후보숫자 X의 잠긴 트리플이 세쌍을 이룰 때 

 2. 잠긴 방향의 직각 방향에 있는 다른 후보숫자 X를 지울 수 있다

 

 

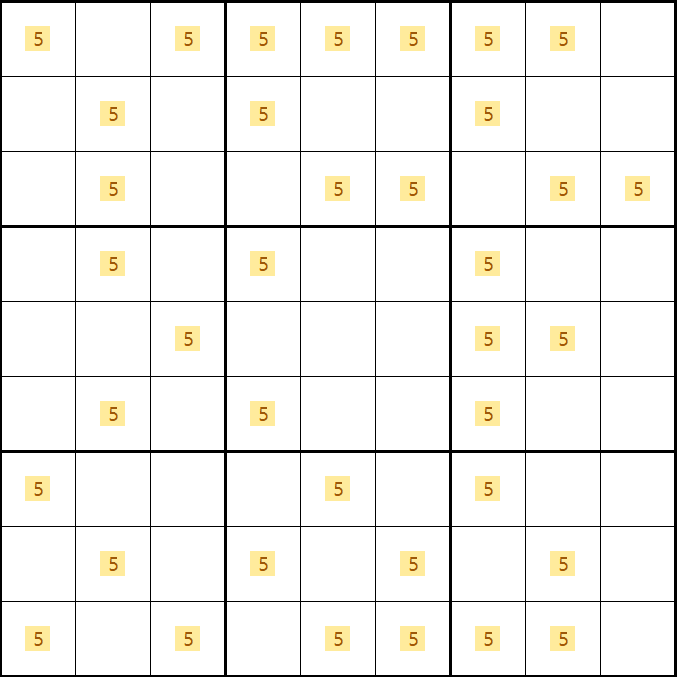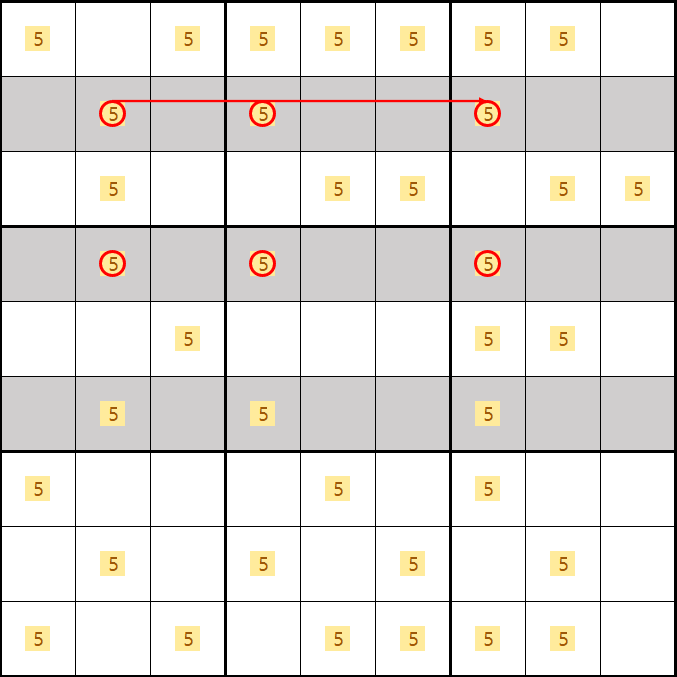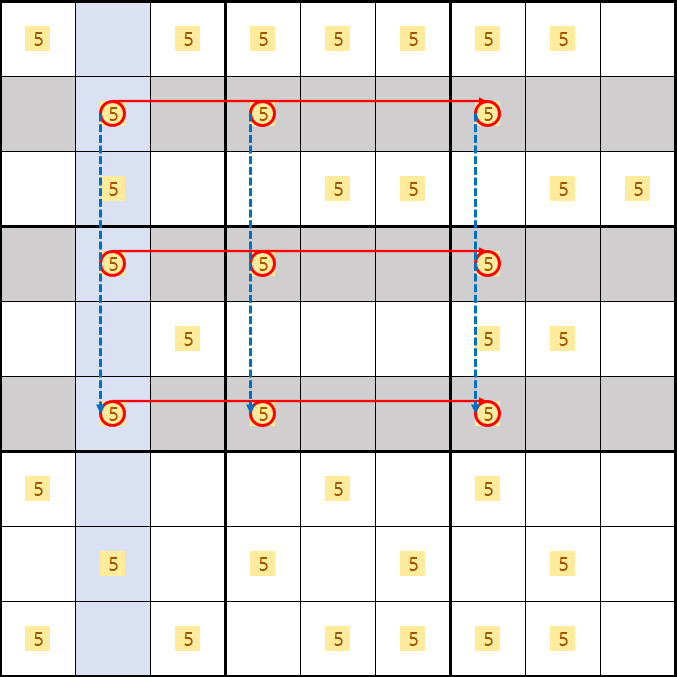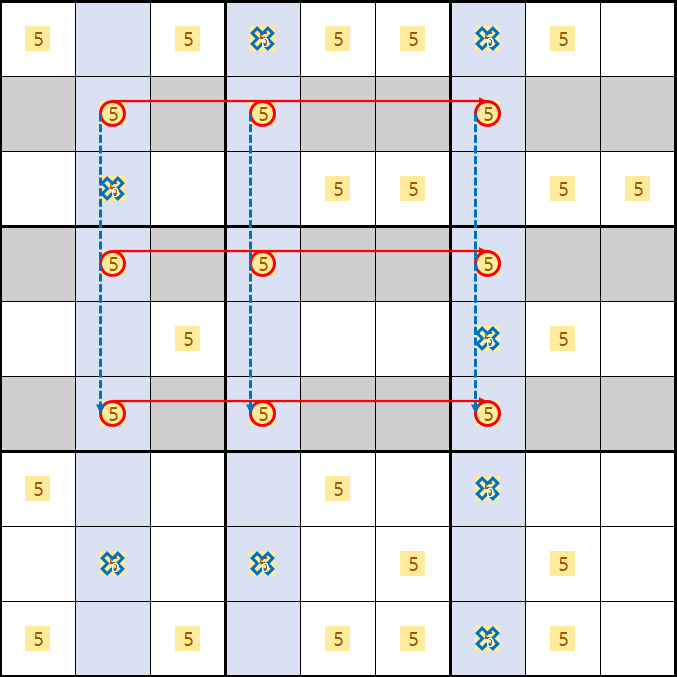
위의 소드 피쉬 다이아그램 움짤을 읽는 방법은 

 

 B행, D행, E행에 후보숫자 5가 2,4,7열에 같은 열로 위치하고 있으면 

 모든 하우스에는 1개의 숫자가 들어갈 수 있기 때문에 

 후보 숫자 5 B2, B5, B7 중 1칸, D2, D5, B7 중 1칸, F2, F5, F7 중 1칸에는 무조건 들어가야 하므로

 

 2열과 4열 및 7열의 의 후보숫자 5를 제거할 수 있다. 

 

 로 리딩이 되는데 

 

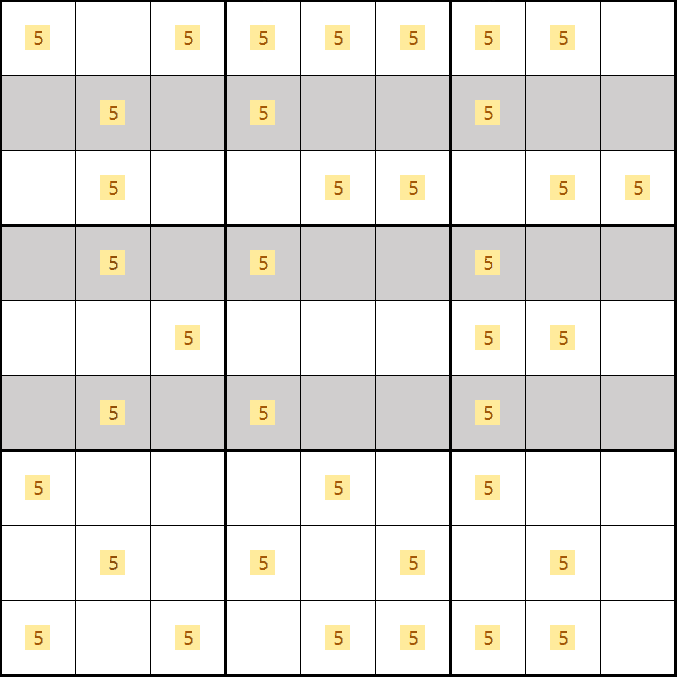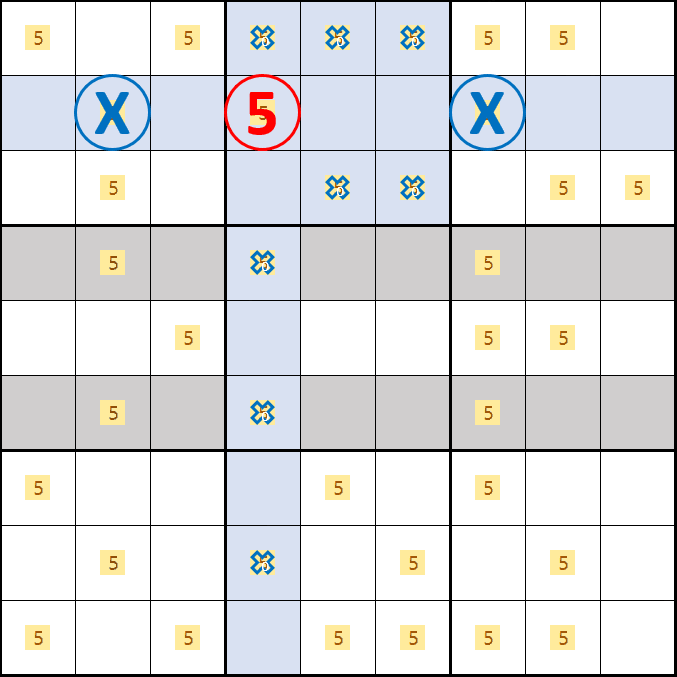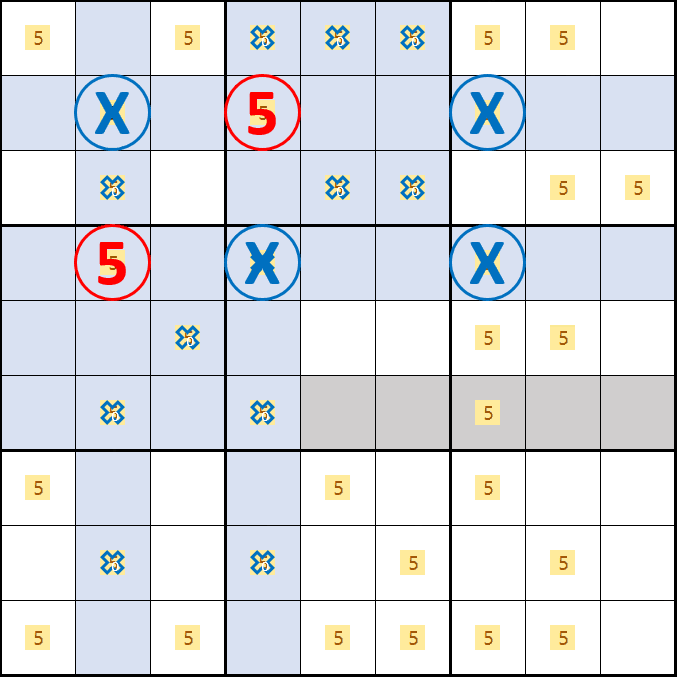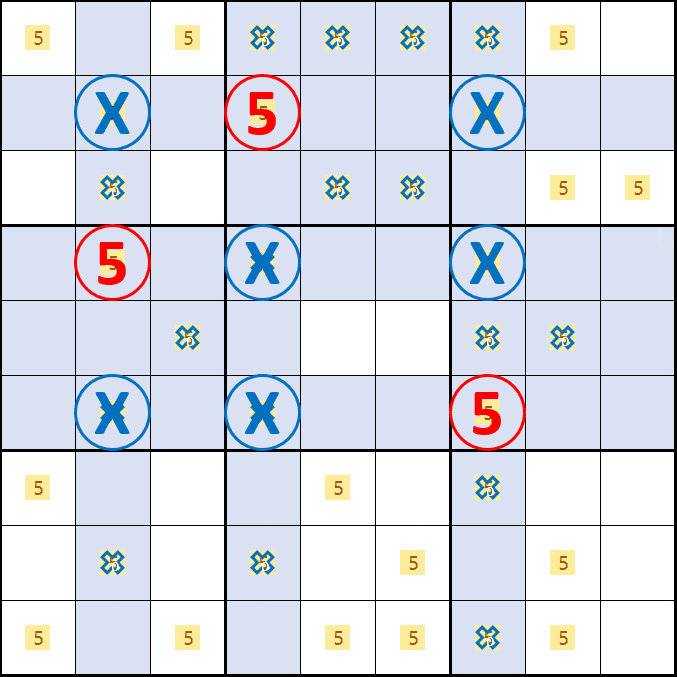
 소드 피쉬는 3 x 3의 칸이기 때문에 경우의 수는 3 x 2 x 1로 아래 움짤처럼 6가지가 나온다. (어떤 경우라도 B, D, F행에는 후보숫자 5가 무조건 1개씩 들어가는 것을 알 수 있다.) 

 

 하지만 위의 경우의 수만 보고는 감이 오지 않을 것 같아서

 후보 숫자 6이 위치하는 경우의 수 6가지 모두를 움짤로 증명해 보면 아래와 같다. (지루해도 재밌는 스도쿠 하려면 읽자!)

 

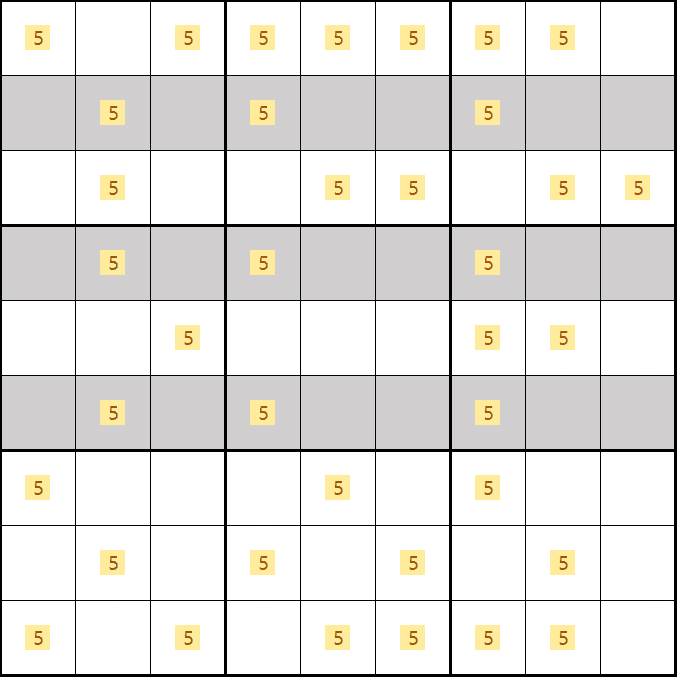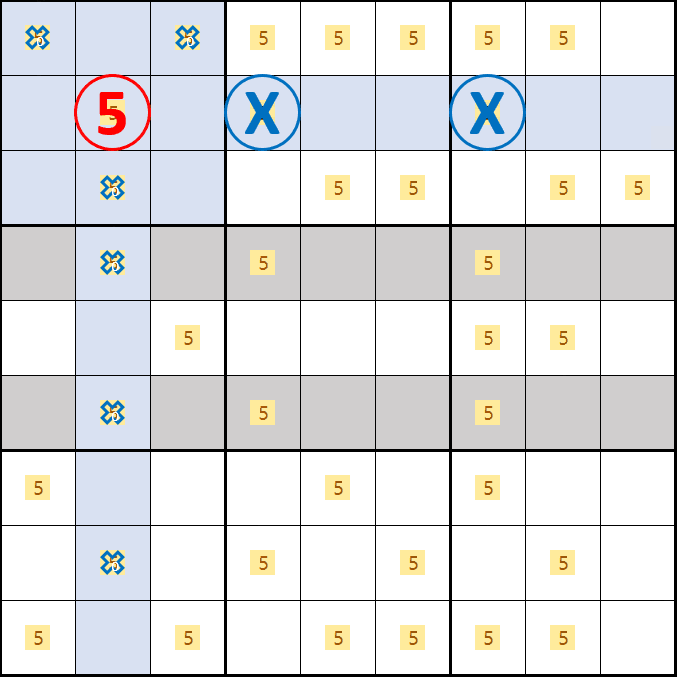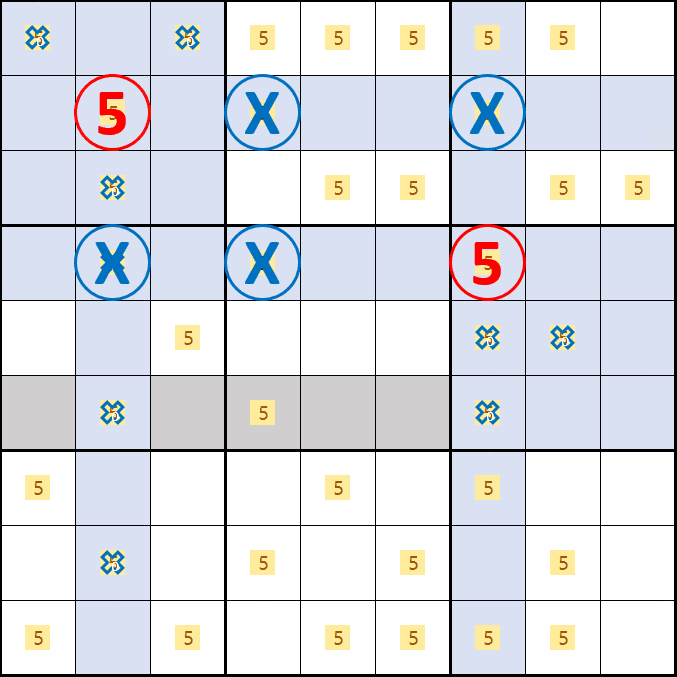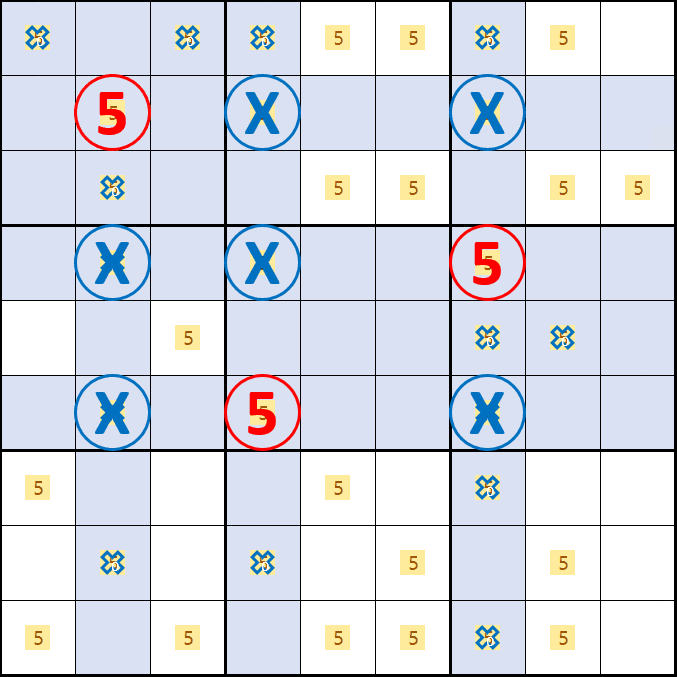
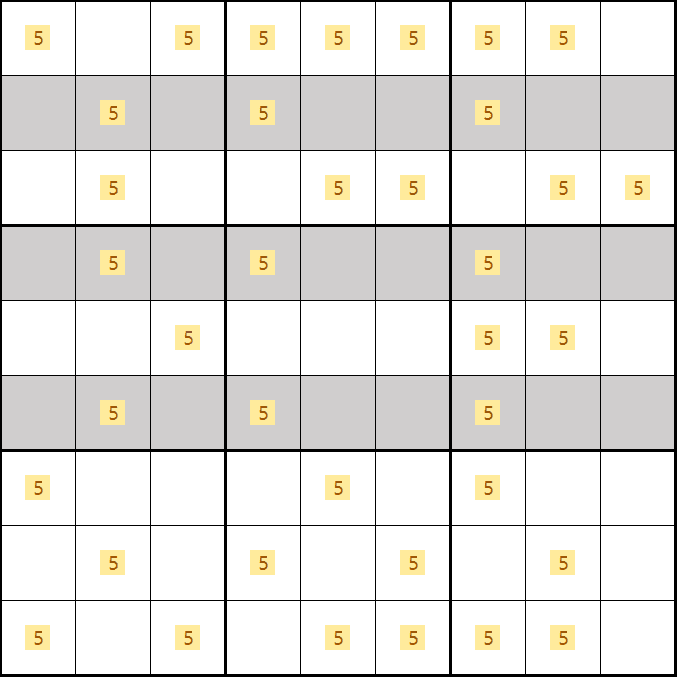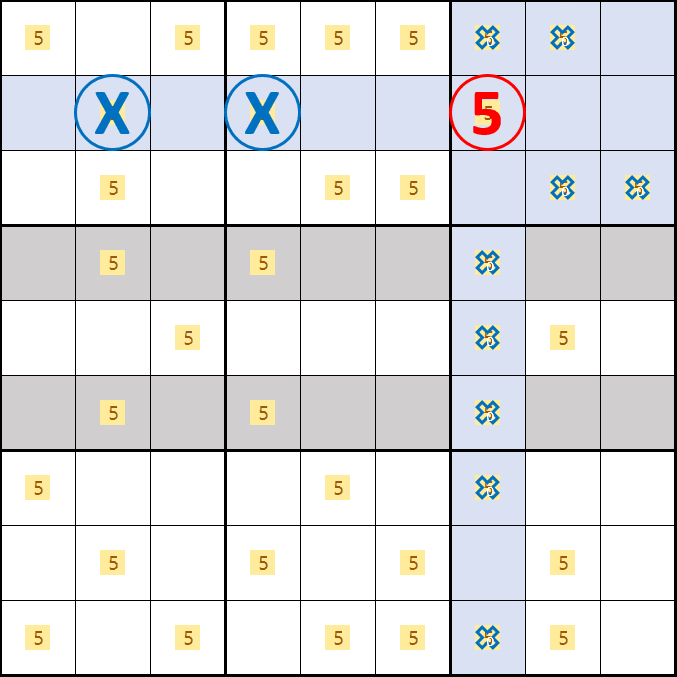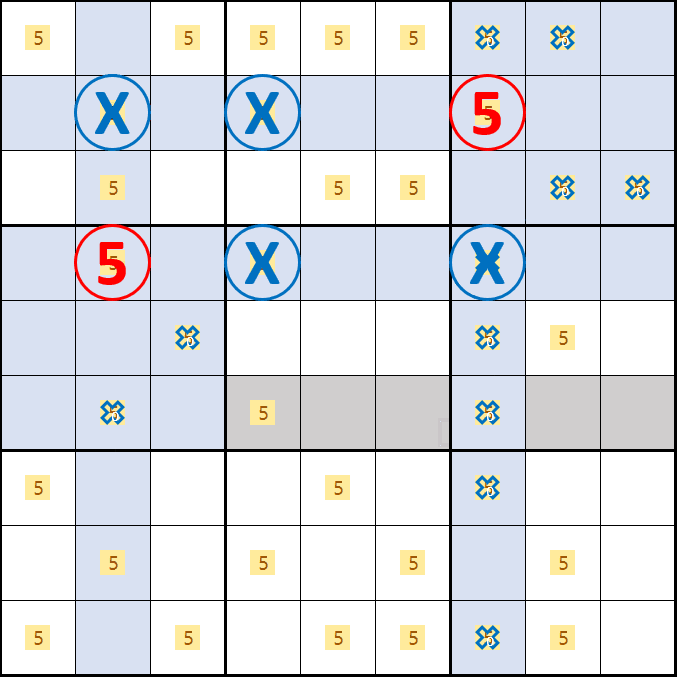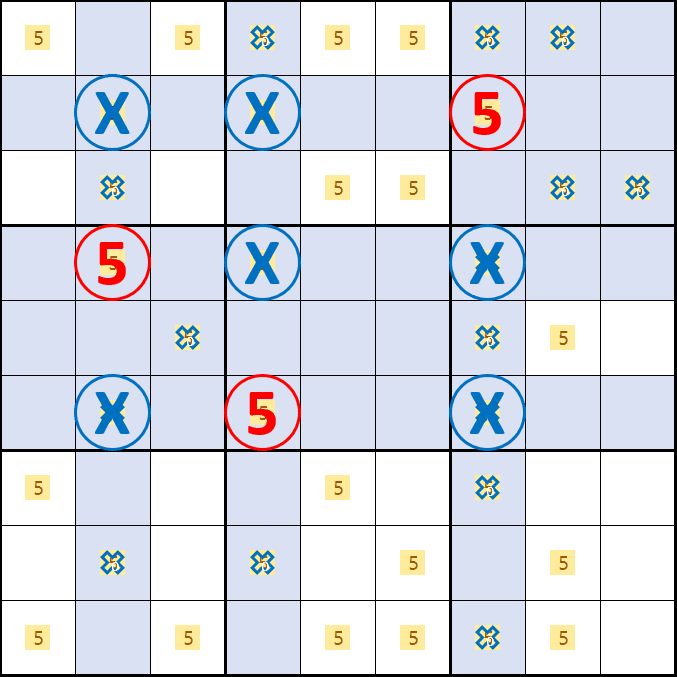
소드 피쉬 증명1. 후보숫자 5가 B2, D4, F7이 되는 경우

 

소드 피쉬 증명2. 후보숫자 5가 B2, E4, D7 이 되는 경우

 

 

소드 피쉬 증명3. 후보숫자 5가 D2, B4, F7 이 되는 경우

 

소드 피쉬 증명4. 후보숫자 5가 D2, E4, D7 이 되는 경우

 

소드 피쉬 증명5. 후보숫자 5가 E2, B4, D7 이 되는 경우

 

 

소드 피쉬 증명6. 후보숫자 5가 E2, D4, B7 이 되는 경우

 

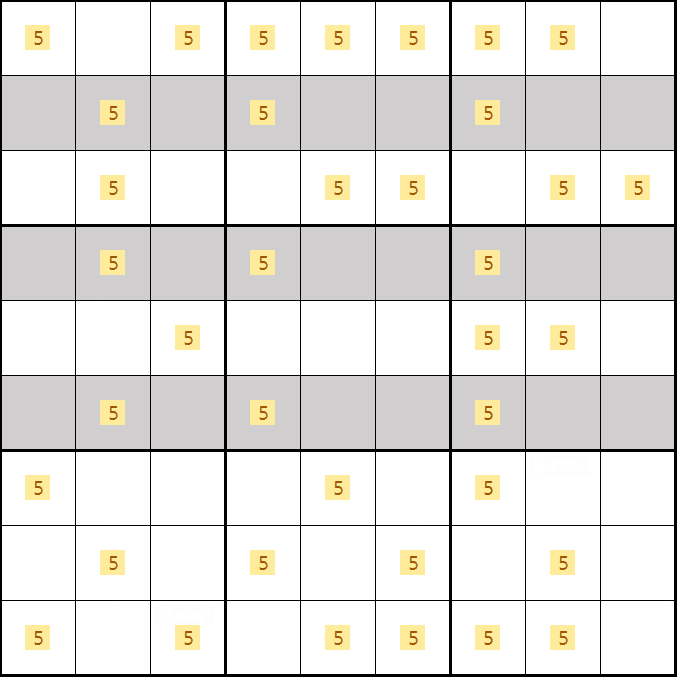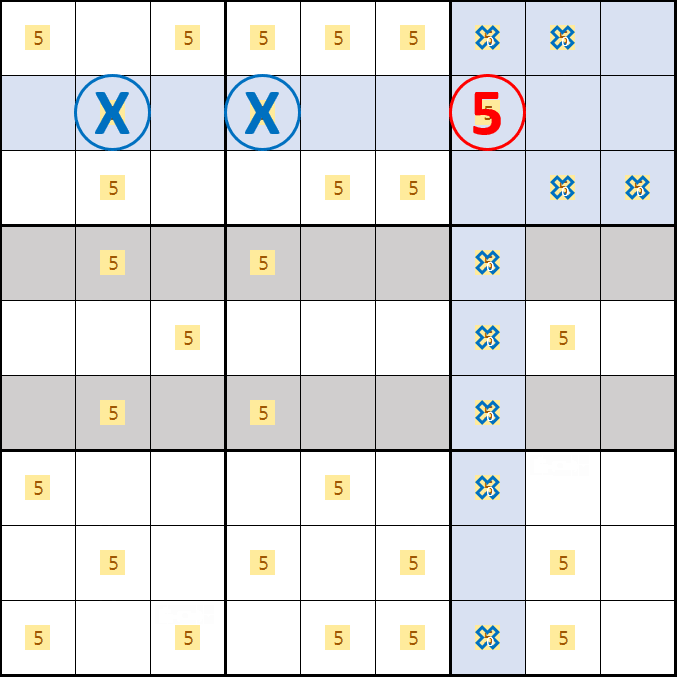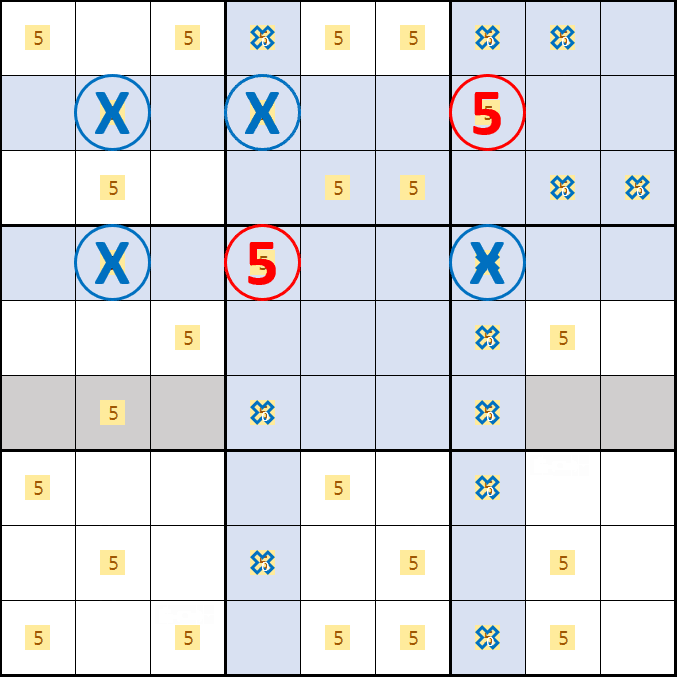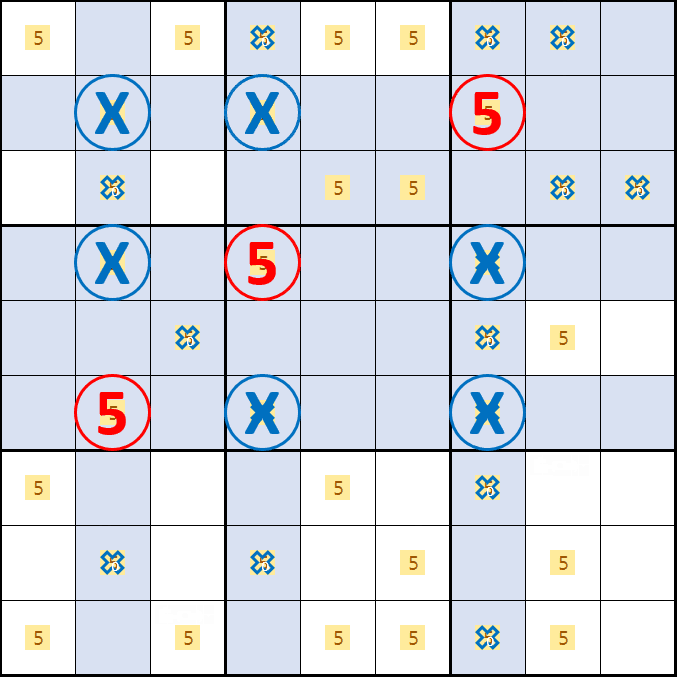
소드 피쉬 증명7. 소드 피쉬 증명1~6까지의 결과만 움짤로 엮으면 아래와 같이

 

1, 3, 5, 6, 8, 9열은 경우에 따라서 제거되기도 하고 않되기도 하는데 반해서

6가지 경우의 수 모두의 교집합에 해당하는 2, 4, 7열의 어떠한 경우라도 제거되는 부분은 변하지 않는 것을 알 수 있다. 

 

 

 

 위의 소드 피쉬 개념을 심화 확장해서 익힐 수 있도록 '스도쿠 솔브'라는 사이트에서 캡쳐해 온 소드피쉬 다이아그램 예제 92개를 움짤로 만들어 올린다. 처음 접해서 알지 못하더라도 자꾸 보면 알게 되고 익숙해 진다. '보고~ 또 보자~' 

 

 

 위의 움짤을 자세히 보고 싶다면 아래 링크로 가서 찬찬히 보면서 익혀 보자.

 

스도쿠 기본공식 패턴 모음 5/소드(젤리) 피쉬 [Sword (Jelly) Fish]

스도쿠 기본공식 패턴 모음 5/소드(젤리) 피쉬 [Sword (Jelly) Fish]

 

3. 젤리 피쉬(Jelly Fish)

 

  젤리 피쉬는 X윙 > 소드 피쉬의 확장판으로 

  4 x 4 사각형의 형태로 나타난다. 

 

 1. 행 또는 열에 대한 후보숫자 X의 잠긴 쿼트러플이 네 쌍을 이룰 때 

 2. 잠긴 방향의 직각 방향에 있는 다른 후보숫자 X를 지울 수 있다

 

 

 리딩을 해보면 B, D, F, H행에 후보숫자 5 - 4개가 잠겨있고

 

 동일한 열에 배열이 되면 

 후보숫자 5는 하우스당 1개는 무조건 들어가야 하는 조건 때문에 

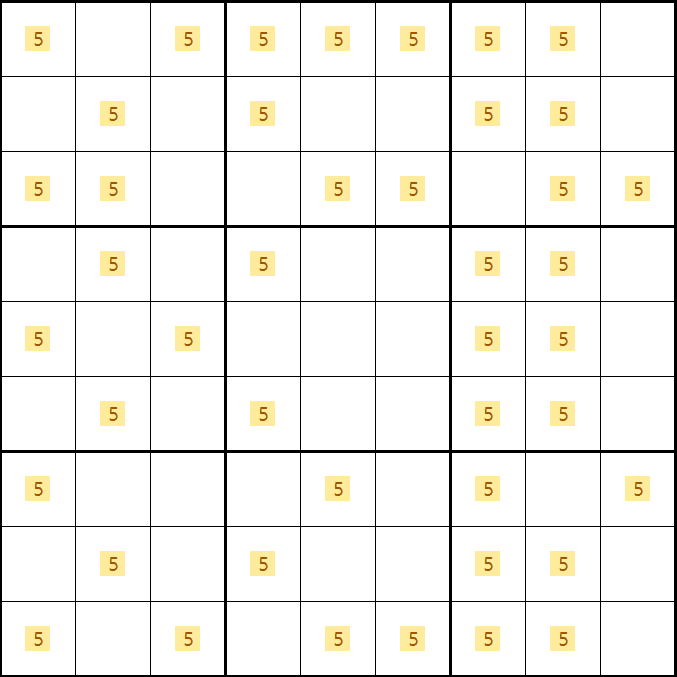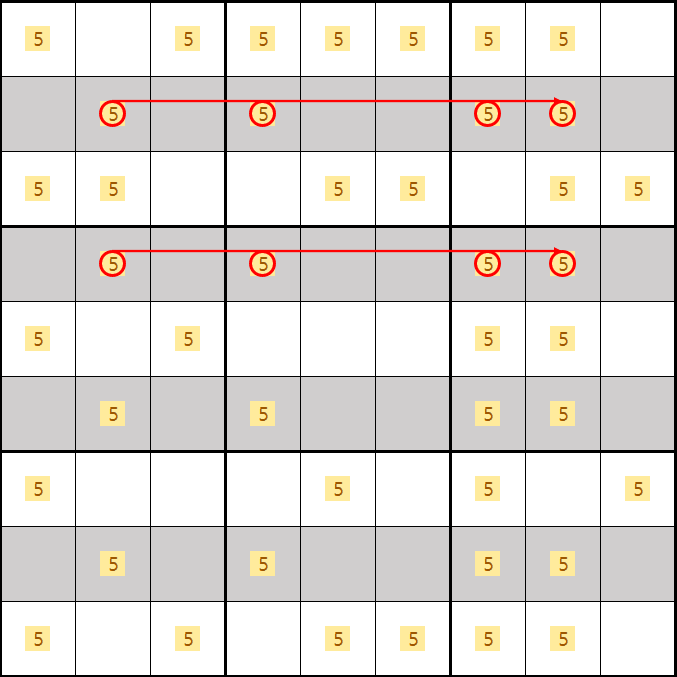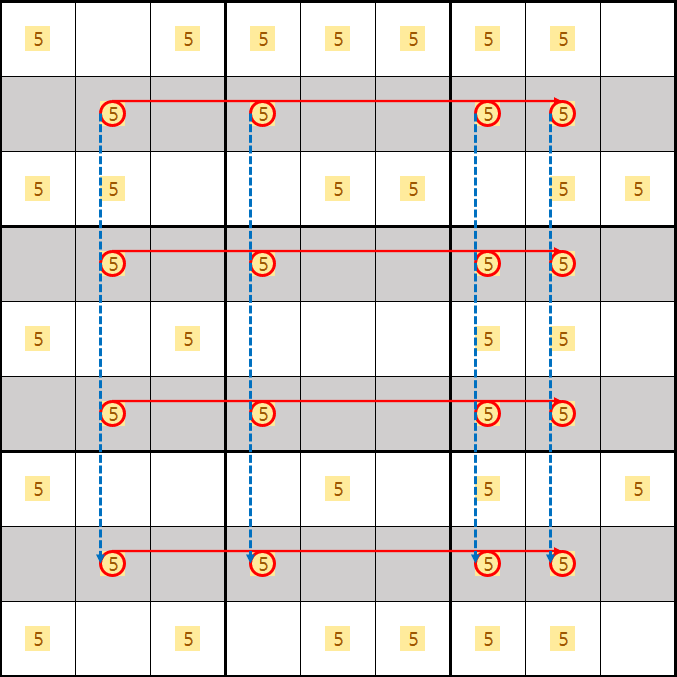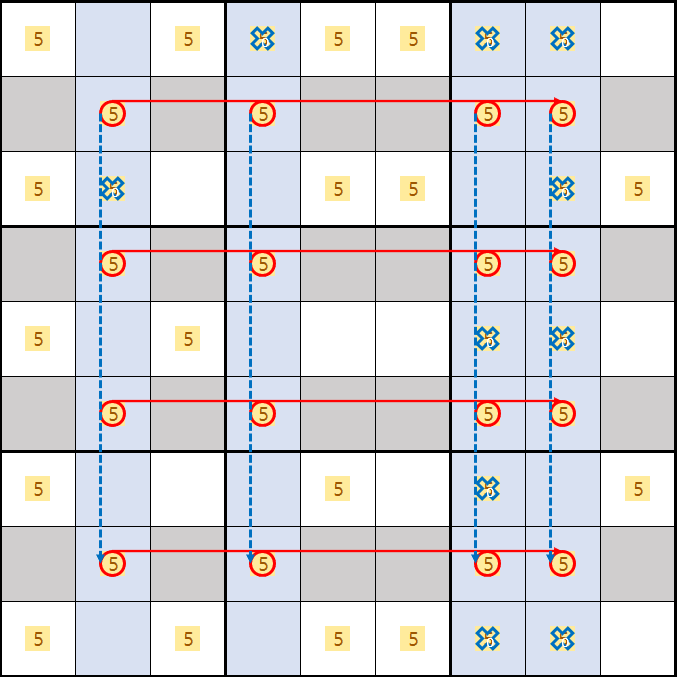
 2, 4, 7, 8열에 후보숫자 5가 들어가야 하므로 

 B, D, F, H행외에 2, 4, 7, 8열에 존재하는 후보숫자 X를 제거할 수 있다. 

 

 후. 위에서 살펴본 X윙과 소드 피쉬는 경우의 수가 1개, 6개로 모든 상황에 대한 검증을 했는데

 젤리피쉬는 아래와 같이 5가 B, D, F, H행에 위치하는 경우의 수가 24개라서 모든 경우에 대한 증명은 생략하겠다. 소드피쉬에서 감을 잡았을 거라 믿겠다. 

 

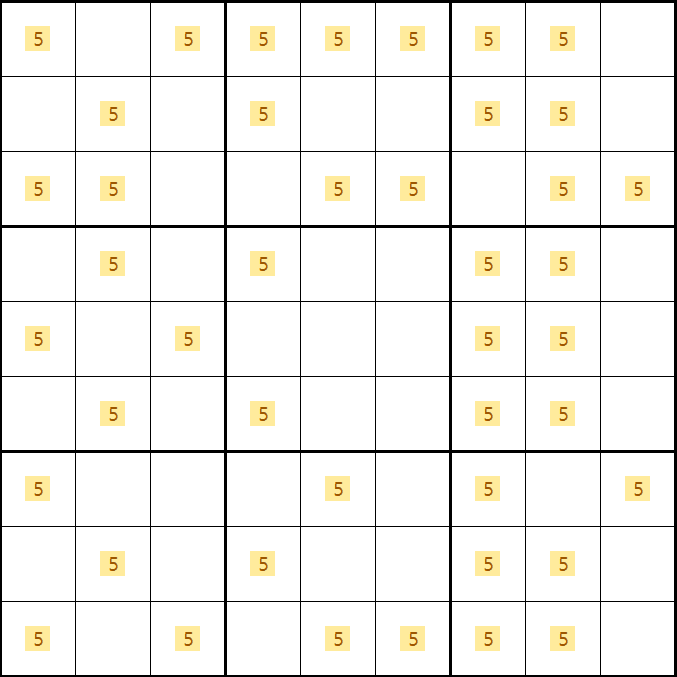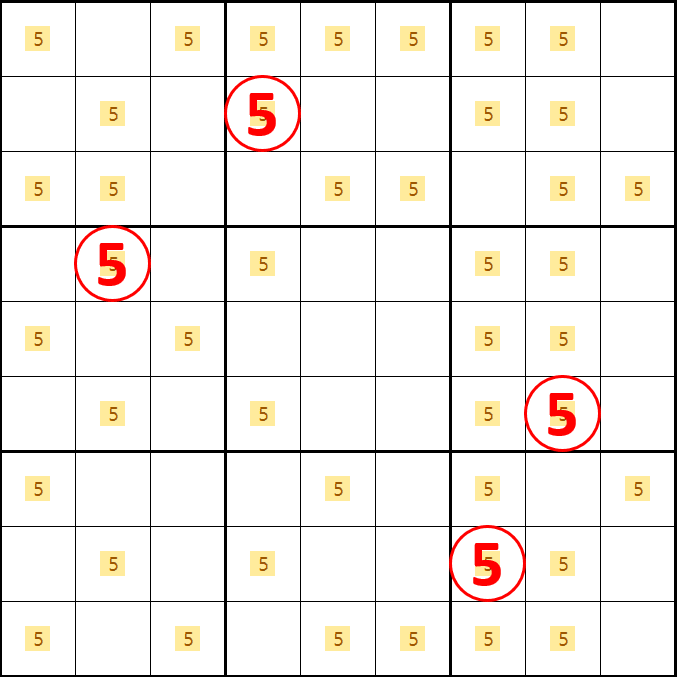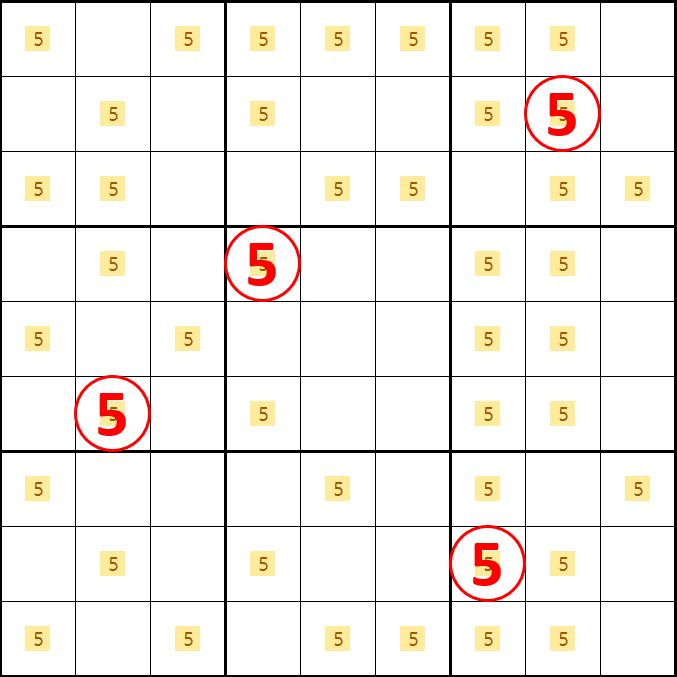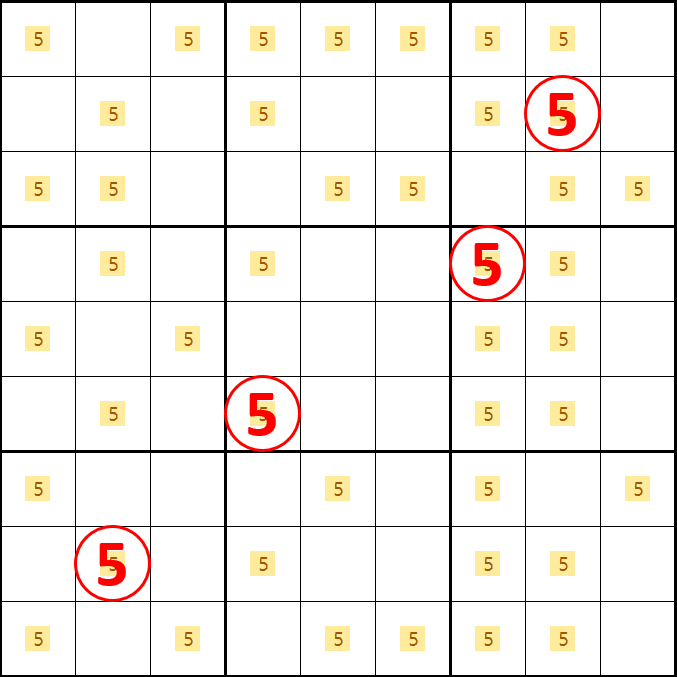
좀 더 눈에 띄도록 숫자만 키워 봤다. 부디~ X윙과 소드윙에서 증명되는 방법을 익혔기를 바란다. 

 

 

젤리 피쉬는 400개의 사례를 조사했을 때, 단 9개만 나왔다. 그래도 귀한 자료이니 움짤로 만들었다. 

 

 

스도쿠 기본공식 패턴 모음 5/소드(젤리) 피쉬 [Sword (Jelly) Fish]

스도쿠 기본공식 패턴 모음 5/소드(젤리) 피쉬 [Sword (Jelly) Fish]

 

---

 

위에서 살펴본 형제 공식 X윙, 소드 피쉬, 젤리 피쉬는 고급 공식 중에 패턴을 찾기 쉬우면서 많이 나오는 것이니 잘 익혀서 더욱 더 재미 있는 스도쿠를 즐겨보길 바래 본다. 

 

 이제 처음에 봤던 움짤을 보면 왜 위의 3개 스도쿠 공식이 형제격인지 이제 알 수 있을 것이다. 

 

Andoku 스도쿠 3 - 강력 스도쿠 추천 앱

Andoku 스도쿠 3 - 강력 스도쿠 추천 앱