움짤로 익히는 스도쿠 8. 유니크 렉탱글 Part 1.(Type1,2)
- 스도쿠/고급
- 2024. 11. 12.
이번 글에서는 명칭과도 같이 유니크한 사각형 스도쿠 공식에 대해 알아 보도록 하겠다. 스도쿠에 입문한지 3개월차인 나는 요즘에 XY 체인 및 AIC 에서 좌절을 좀 하고 있다. 그래서 XY체인을 좀 더 쉽게 찾는 방법을 서칭하다가 유니크 렉탱글이라는 공식을 알게 됐고, 매우 단순하지만 이해만 하면 아주 강력한 힘을 지니고 있는 것도 알게됐다. 얼마나 간단하면서 강력한지 일단 뒤에 자세히 설명할테니 가볍게 아래 움짤 예제를 보자.
유니크 렉탱글은 체인 기술을 알면 좋지만 공식으로 쓰일 정도로 정형화 되어 있기 때문에 체인 기술을 잘 몰라도 쓸 수 있다.
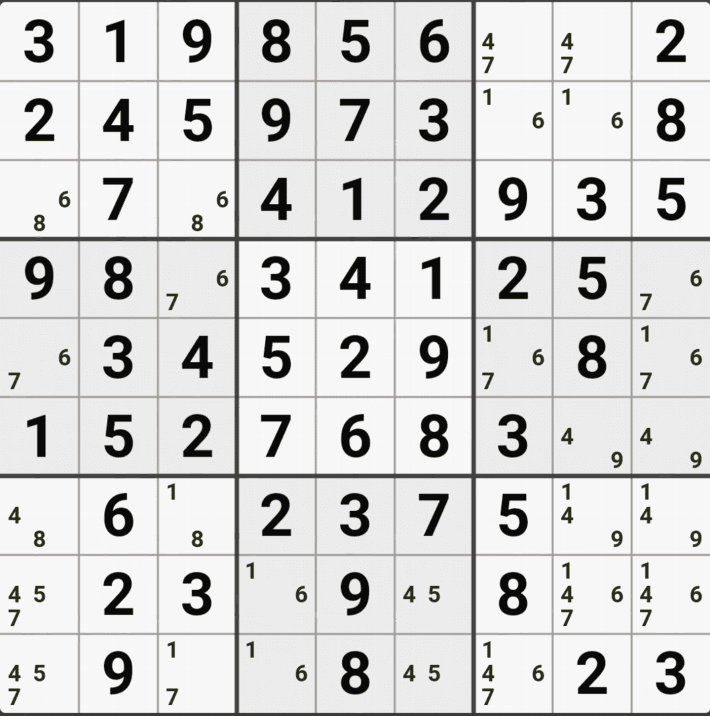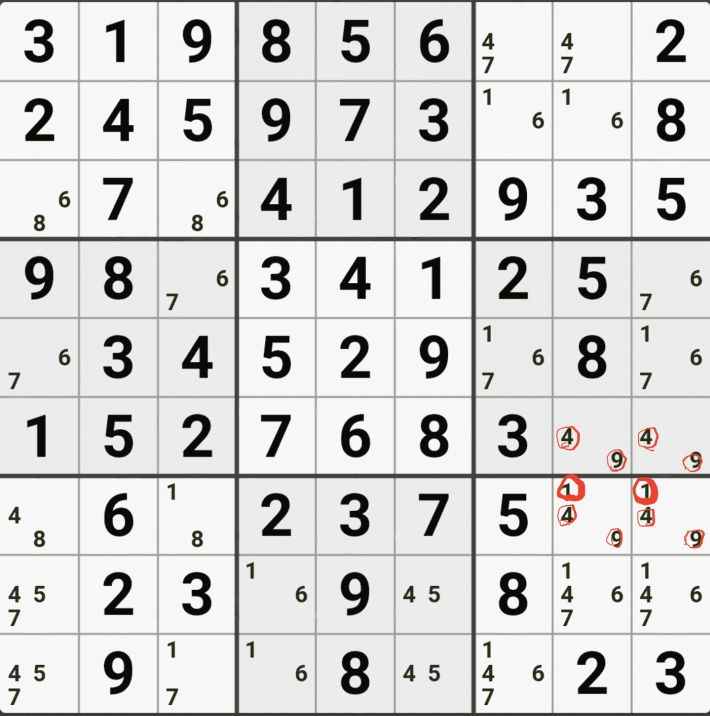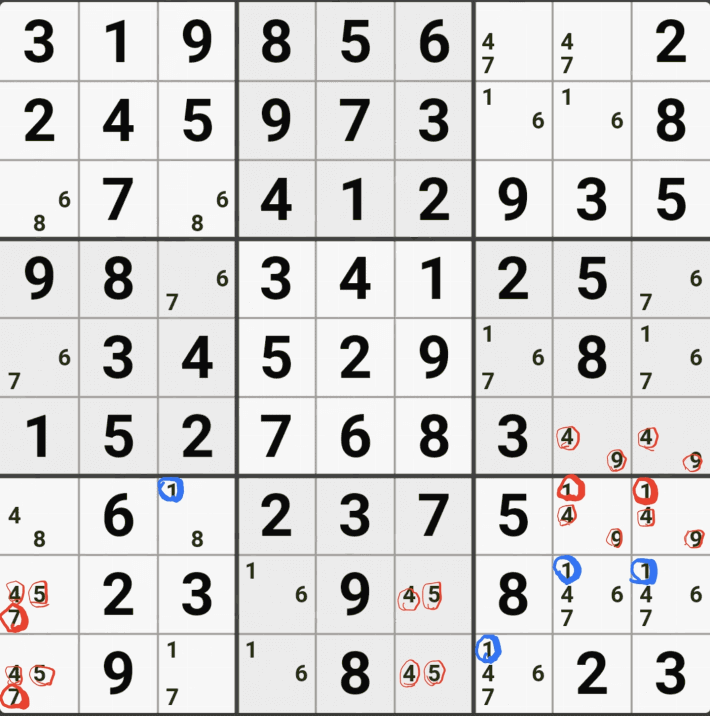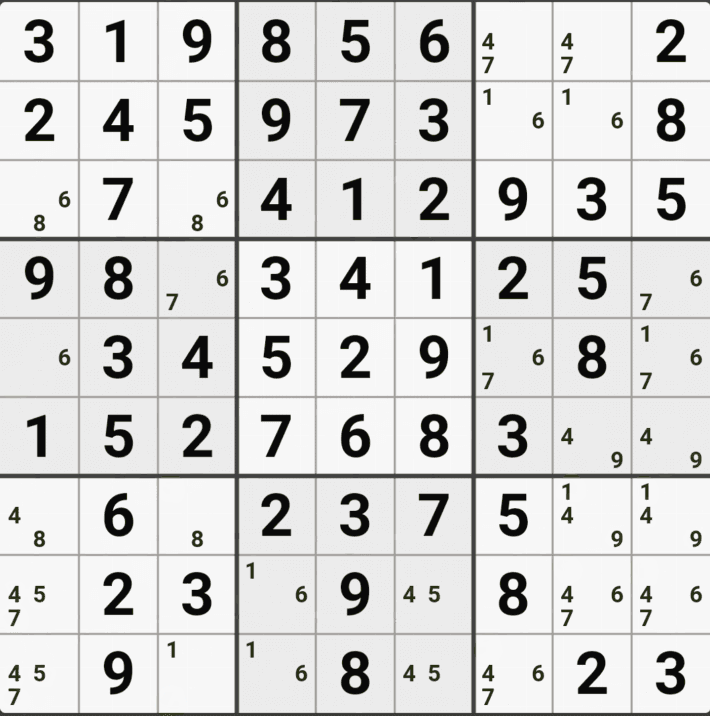
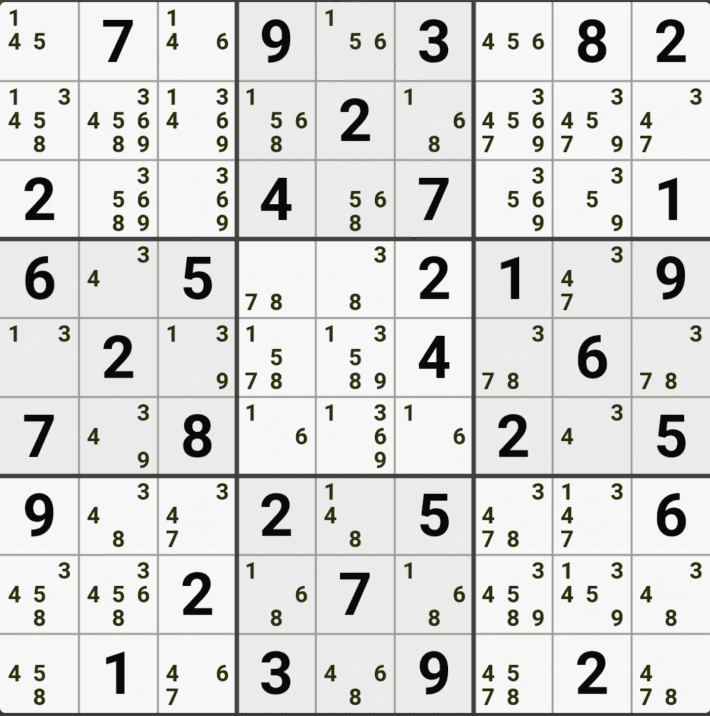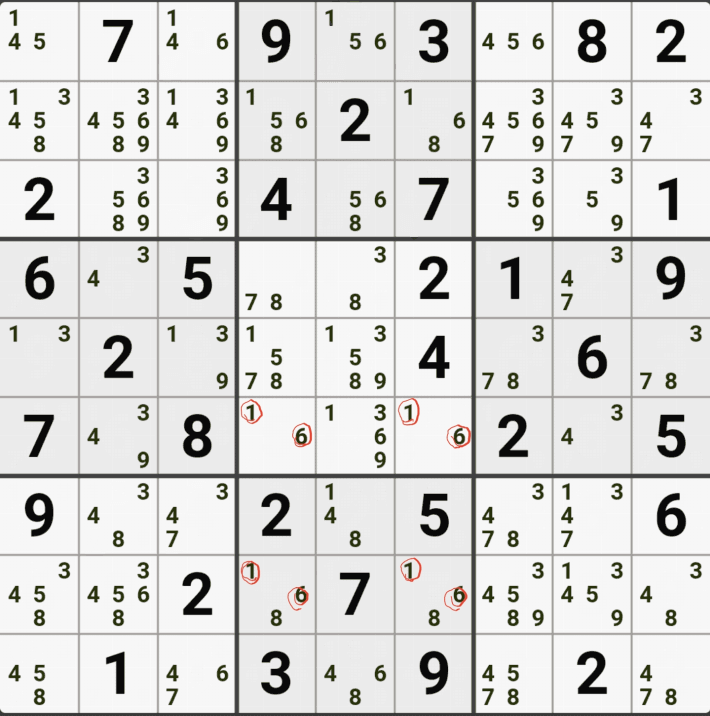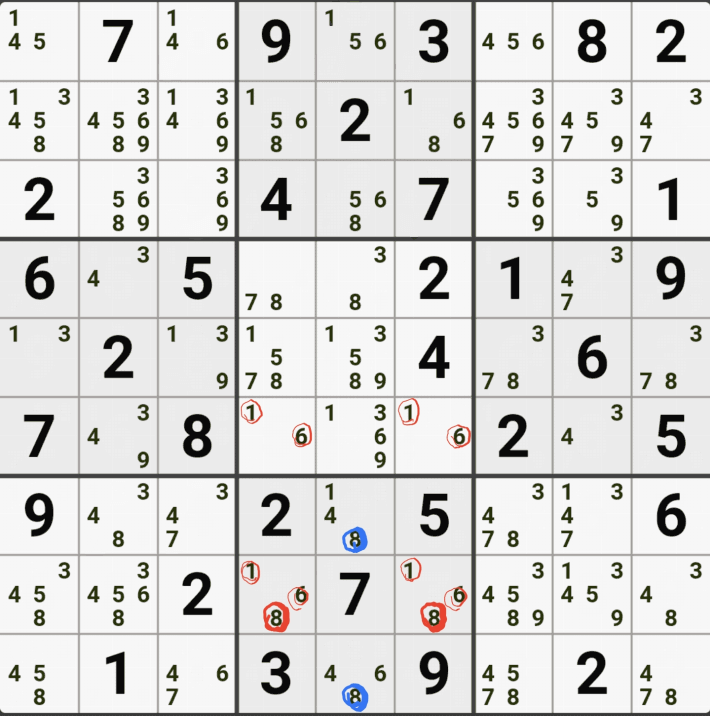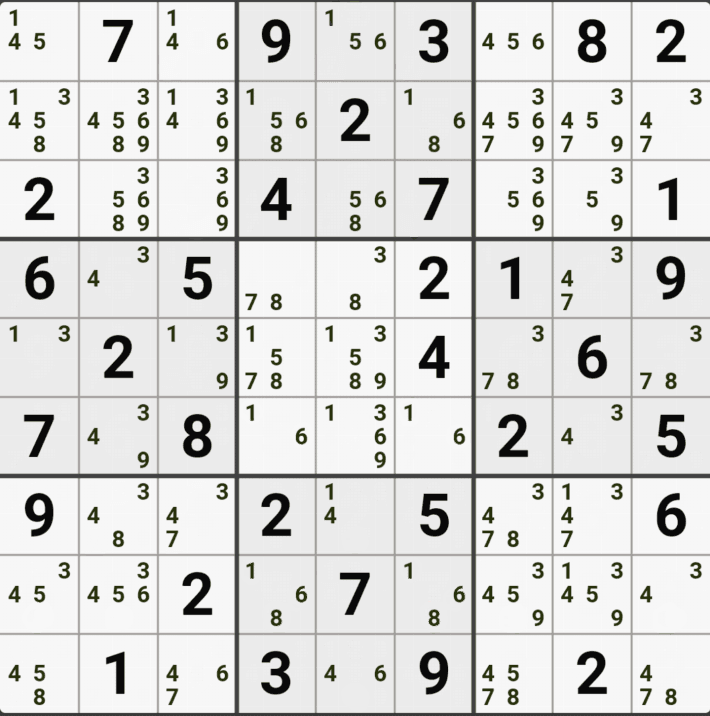
아래 움짤을 보면

박스 7,8,9에 있는 후보숫자 8을 제거하기 위해서
8[G5] AIC
8[H2] 그룹 X체인
8[H7]& 8[H9] X체인
8[I5] 루프체인
8[H1] 페어제거
총 5개의 공식을 사용한 것이다.
이렇게 고급공식 4개와 기초공식 1개를 써서 박스 7,8,9에 있는 후보숫자 6개를 제거했는데
이를 한방에 가능하게 해주는 기술이 있었으니~
바로 유니크 렉탱글이다.

위의 움짤은 처음에 본 공식 5개를 한방에 쓴 것과 같은 효과를 내는 유니크 렉탱글 Type2이다. 이걸 5개 공식을 써서 풀어 낸 것을 보면 알겠지만 링크로만 설명은 불가능 하다. 증명을 위해서 빌려온 개념은 '답은 1개만 존재한다'는 스도쿠 기초 규칙이다.
-유니크 렉탱글 (Unique Rectangles)
의 개념은 이렇다. 아래 움짤과 같이 마지막 4개의 칸에 후보숫자 6/8만 들어 가게 되면 답이 2개가 된다.

즉, 위와 같은 상황은
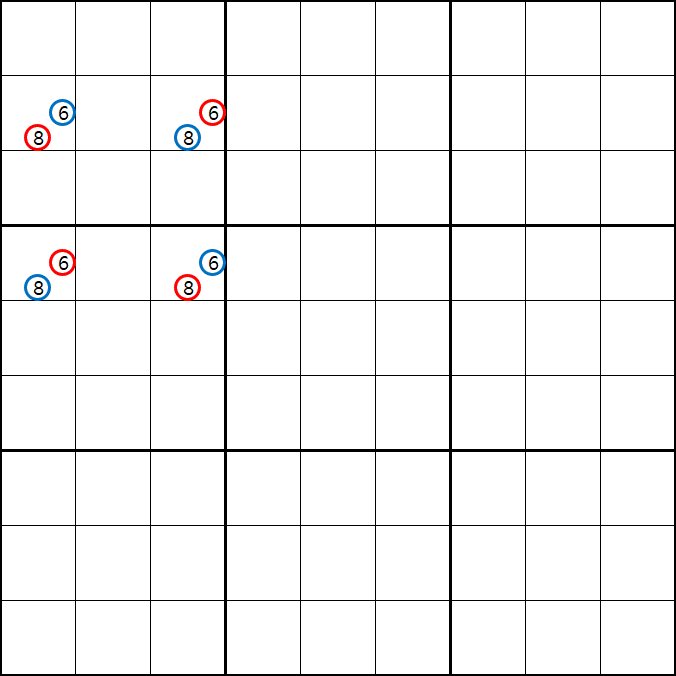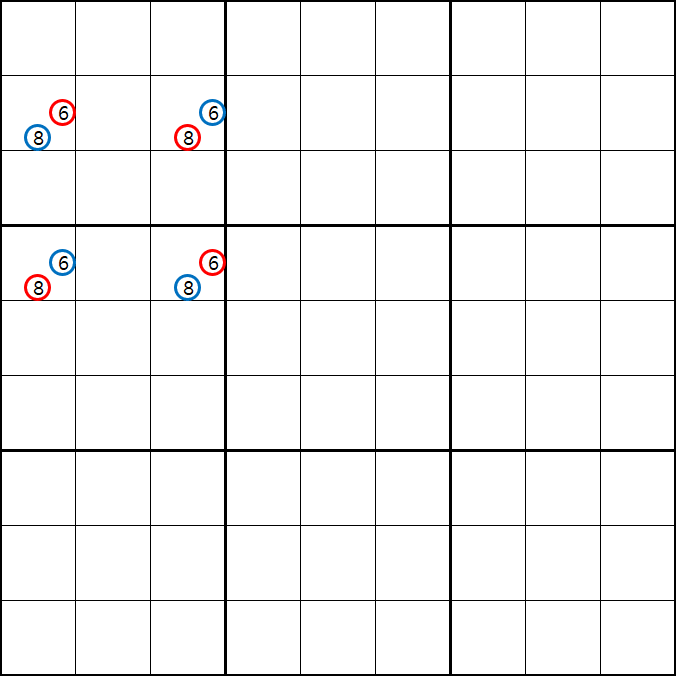
스도쿠 제 1원칙 '모든 칸에는 후보숫자 1개가 반드시 들어간다.'는 충족하지만
제 2원칙인 '답은 1개만 존재한다.'는 규칙에 위배되는 경우다.
따라서 실제 인게임에서 위와 같이 4개의 사각형을 이루는 꼭지점에 동일한 후보숫자 XY만 동시에 존재하는 경우는 모순되는 경우가 생기면 안된다는 성질을 이용하는 공식이 유니크 렉탱글이다.
유니크 렉탱글은 5가지의 유형이 존재하는데 나는 아직 1번과 2번까지만 이해를 해서 이 두 가지에 대한 설명과 예제만 올리고 나중에 나머지 3개를 이해하게 되면 다시 글을 쓰겠다.
유니크 렉탱글 규칙
1. 사각형을 이루는 칸은 2개의 박스에 존재할 것
2. 1개의 박스안에 있는 2개의 칸은 플로어(Floor)라고 칭하고, XY / XY 의 이중링크가 존재할 것
3. 나머지 1개의 박스안에 있는 2개의 칸은 루프(Roof)라고 칭하고, XY / XYZ(XYZW...) 또는 XYZ / XYZ 또는 XYZ / XYW 등의 위크 링크 형태로 존재할 것
물론 위의 2,3번은 변형되어 좀 더 복합적으로 바뀔 수도 있다. 하지만 대체로 위의 규칙을 따른다.
4. 주변에 동일한 후보숫자가 있더라도 2개의 행, 2개의 열에 조건만 만족하면 적용
5. 4개의 칸에 답이 2개가 되는 모순된 상황이 발생하지 않도록 할 것
역시 스도쿠는 말로 이해하기도 어렵지만 설명하기도 어렵다.
유니크 렉탱글 Type 1 - 제일 간단한 유형
Floor : XY / XY
Roof : XY / XYZ 형태
움짤1.
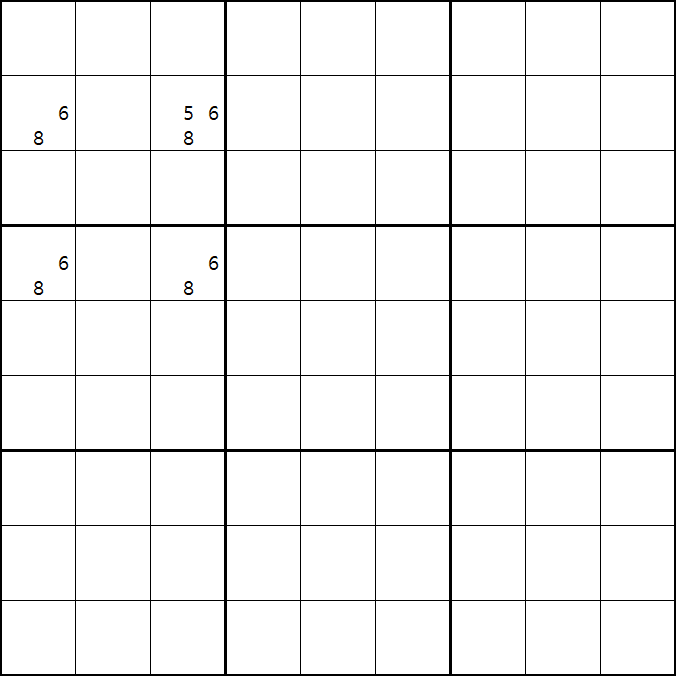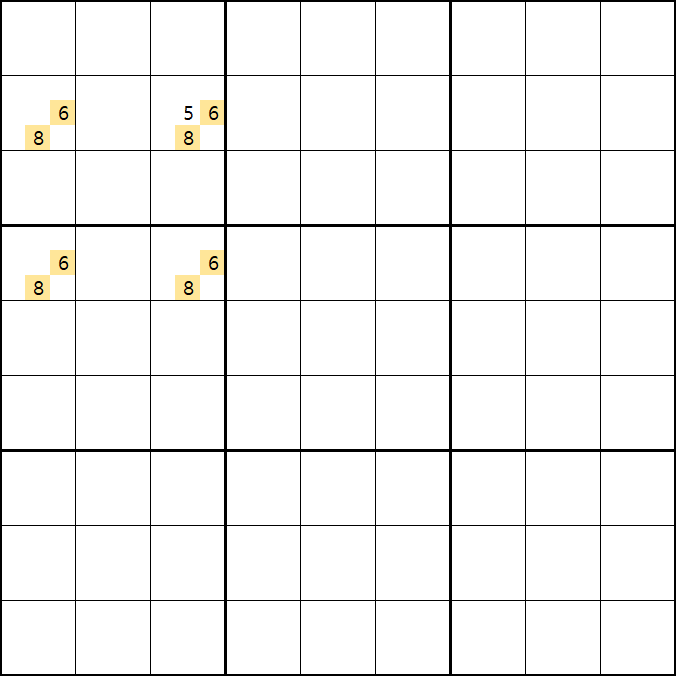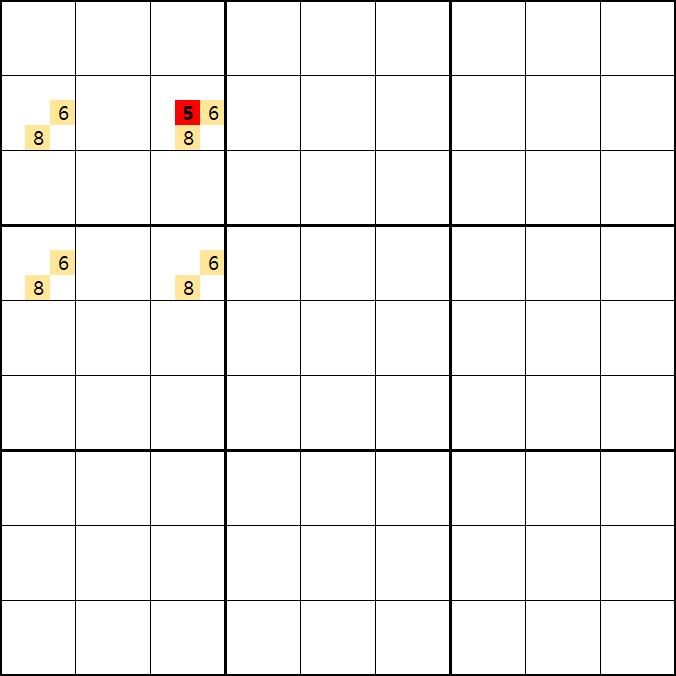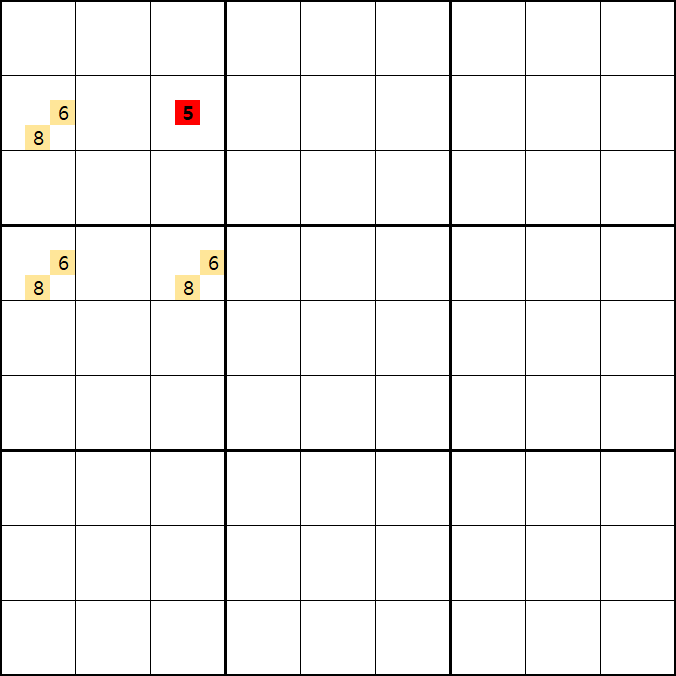
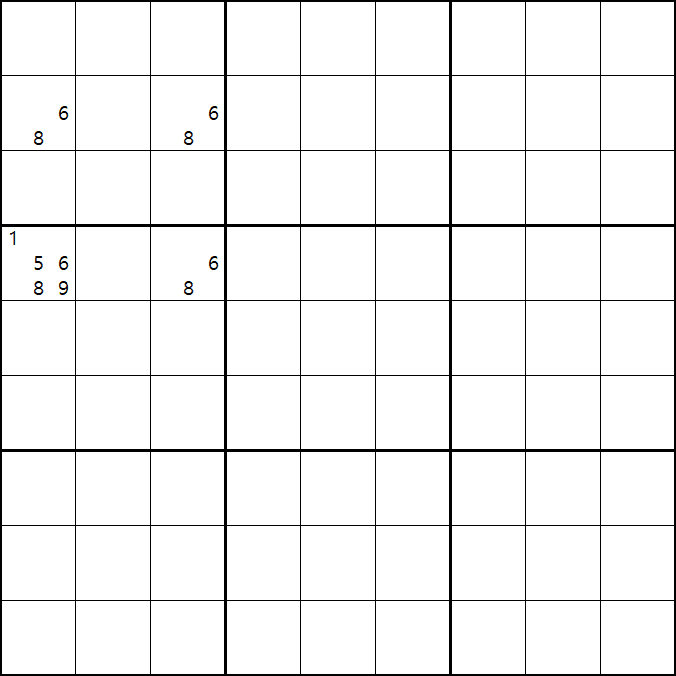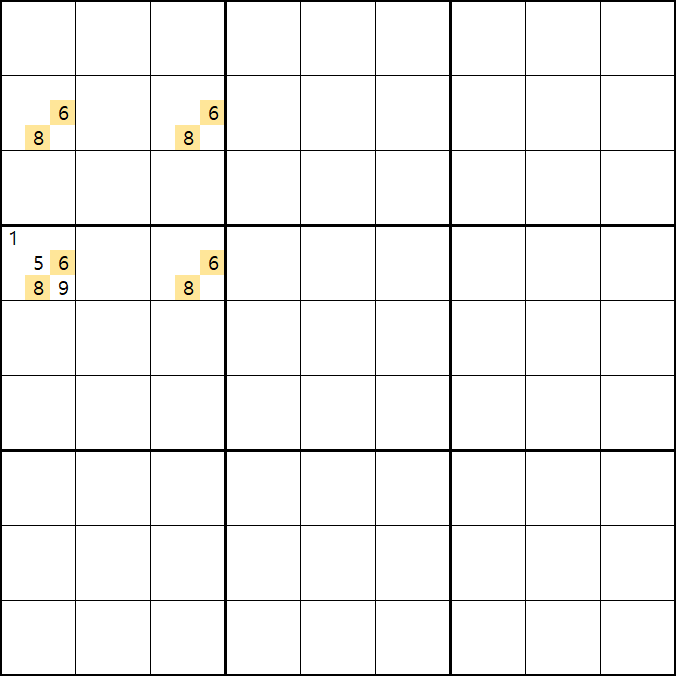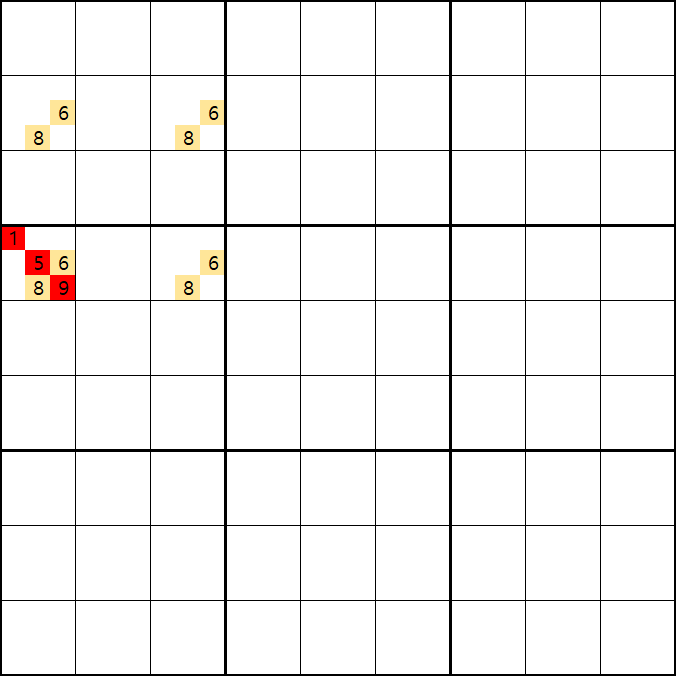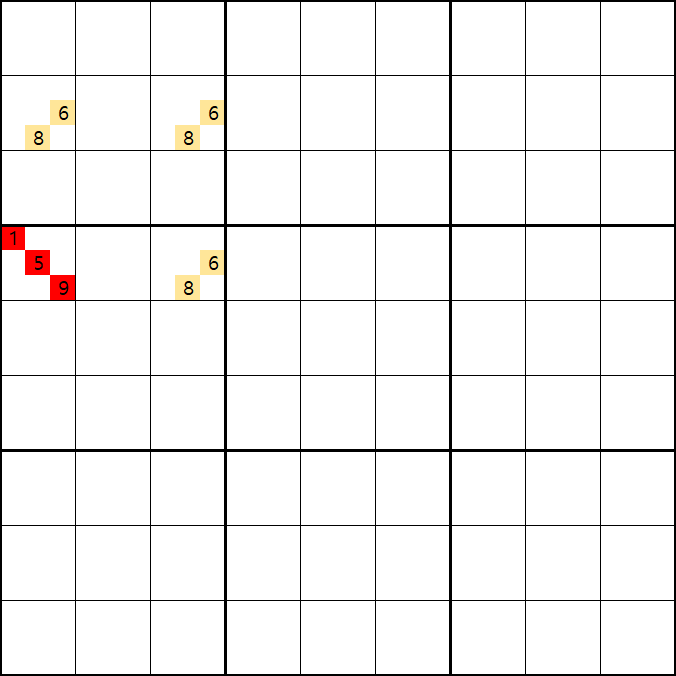
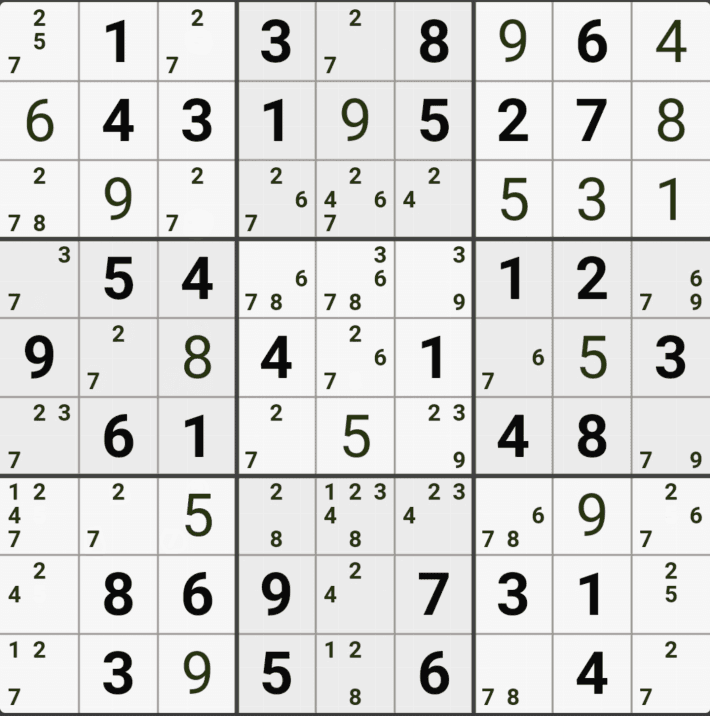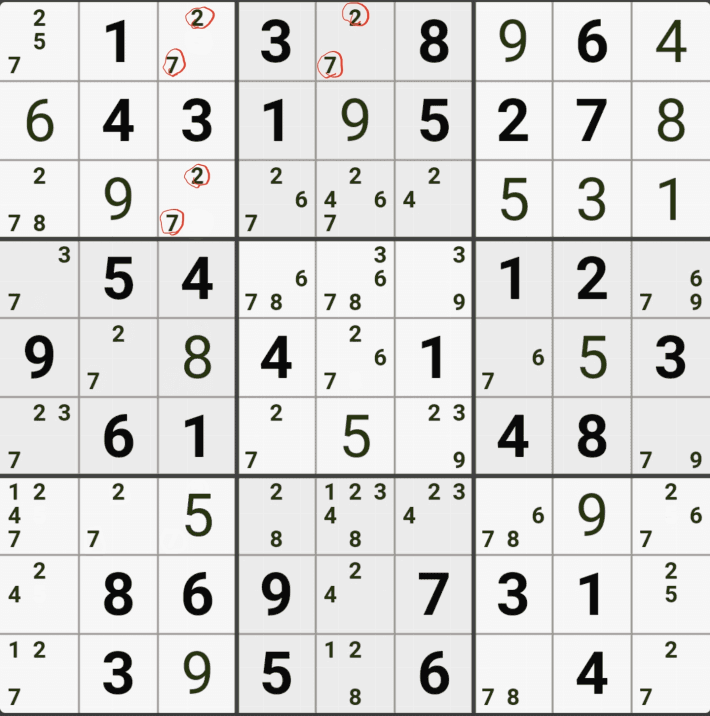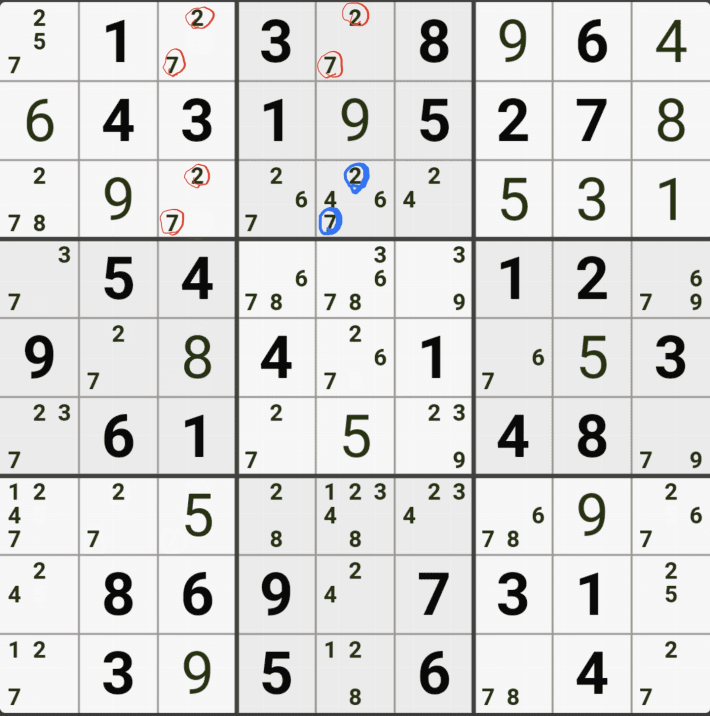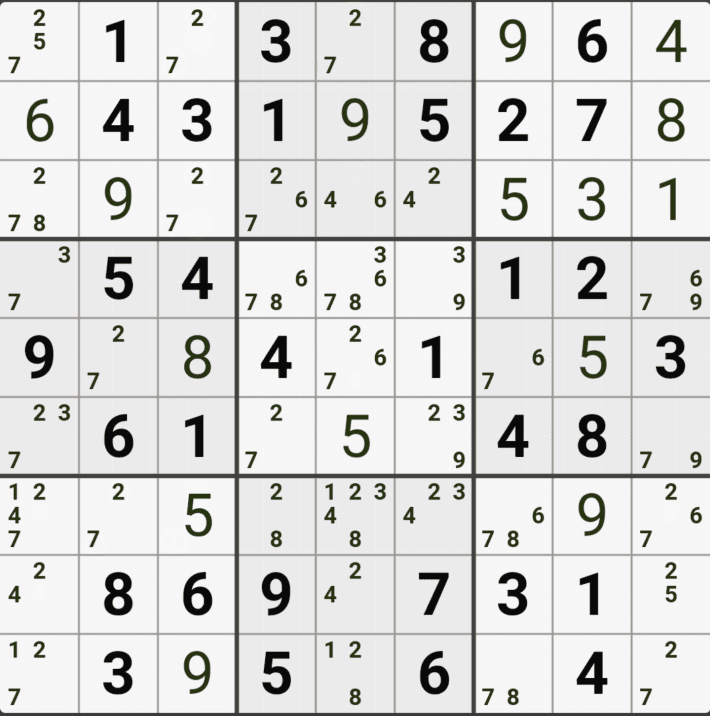
위의 움짤과 같이 사각형을 이루는 4개의 칸에 6/8[B1], 5/6/8[B3] , 6/8[D1], 6/8[D3]에 존재할 때,
B3에 6또는 8이 들어가면 바로 위에서 설명한 답이 2개가 되는 모순된 상황이 생기게 되므로
모순된 상황을 제거 하기 위해서 6[B3]과 8[B3]을 제거할 수 있다. 즉, B3에는 반드시 5가 들어가야만 한다.
고만 쓰면 이해가 되지 않을 거 같고 뒤에 나오는 타입2~5까지 이해하려면 좀 더 정확한 개념을 알기 위해 링크로 증명해 본다. (11월 17일추가)
증명을 위한 움짤은 동시에 만들어 봤다. 박스1,4가 증명1에 쓰이고, 박스 2,5가 증명2에 쓰인다.
증명 1.
+6[B1] -8[B1] +8[D1] -6[D1] +6[D3] -8[D3] 이 되어 -6[B3]을 제거할 수 있고 B3의 5 또는 8중에 해가 있다.
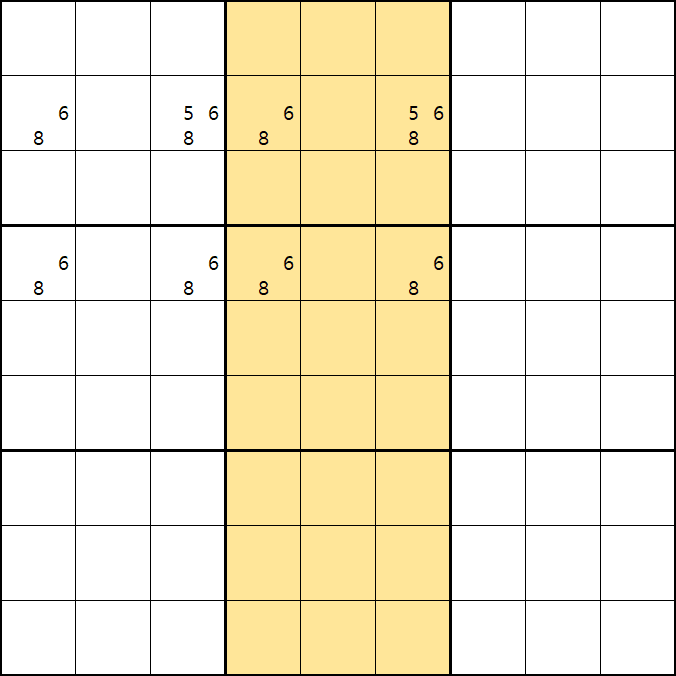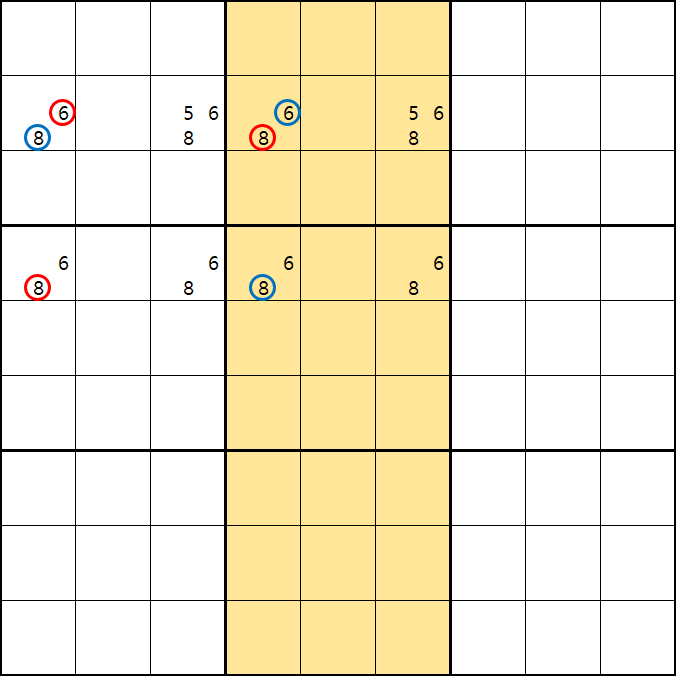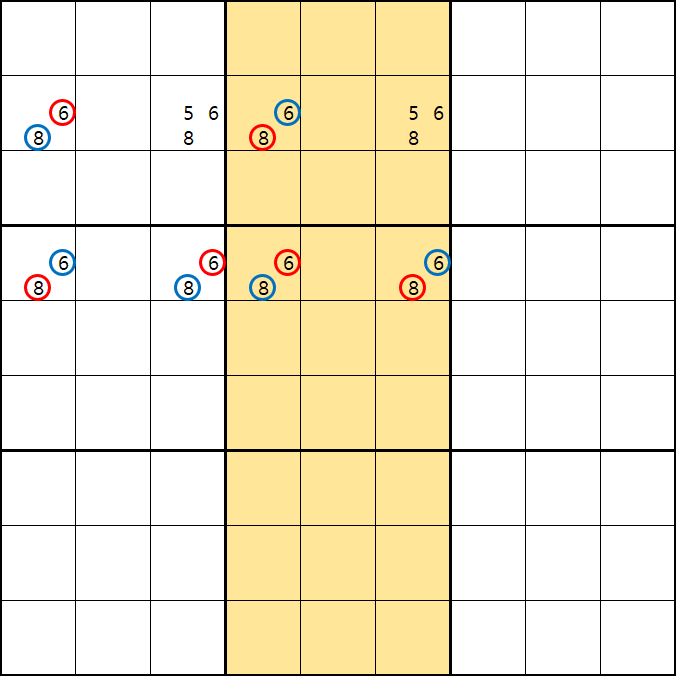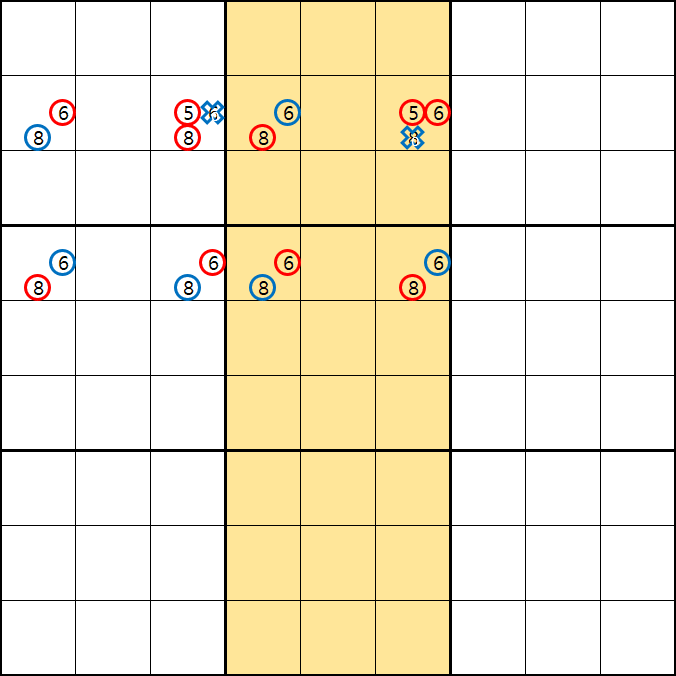
증명 2.
-6[B4] +8[B4] -8[D4] +6[D4] -6[D6] +8[D6] 이 되어 -8[B6]를 제거 할 수 있고 B6의 5 또는 6중에 해가 있다.
증명1에서 5 또는 8중에 해가 있고, 증명 2에서 5 또는 6중에 해가 있는데, 언제나 참이 되는 것은 5가 해가 되는 것이므로 후보숫자 6과 8을 제거할 수 있다. 위의 증명1.2의 결과만 한개로 합쳐봤다. 개념이 낯설겠지만 꼭 이해하고 넘어가자~
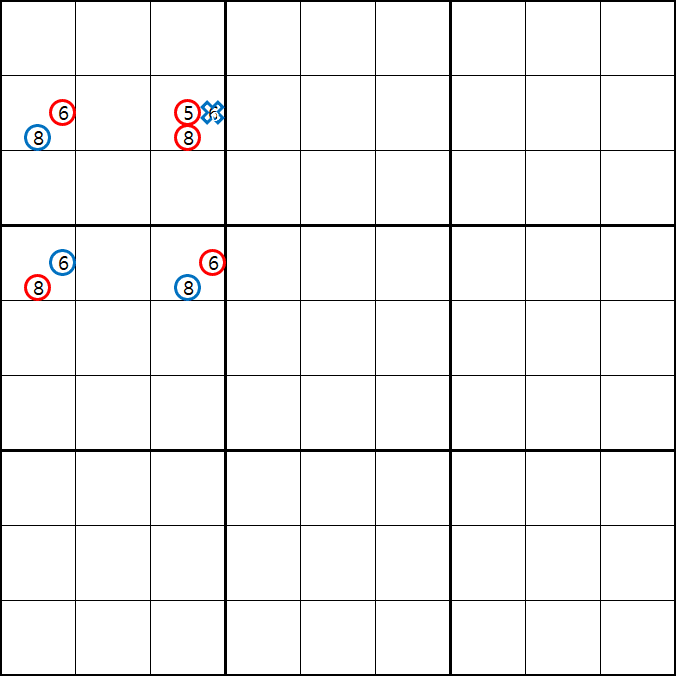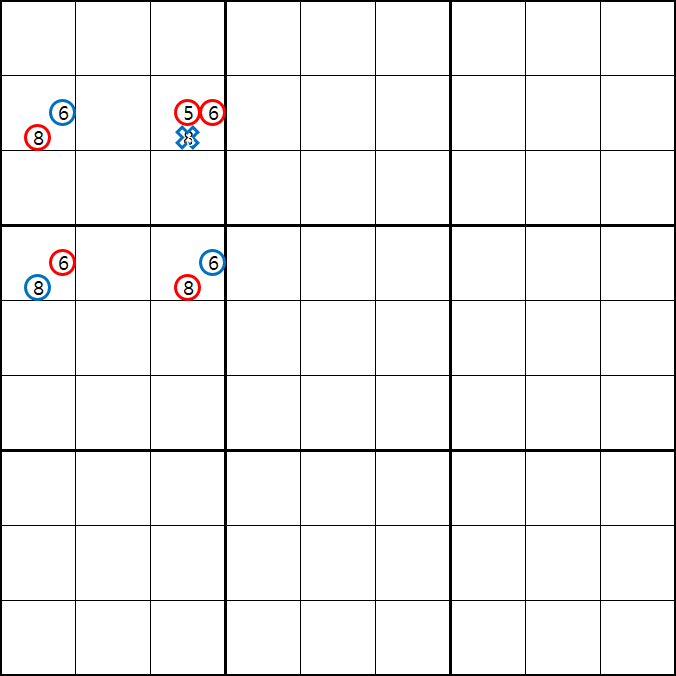
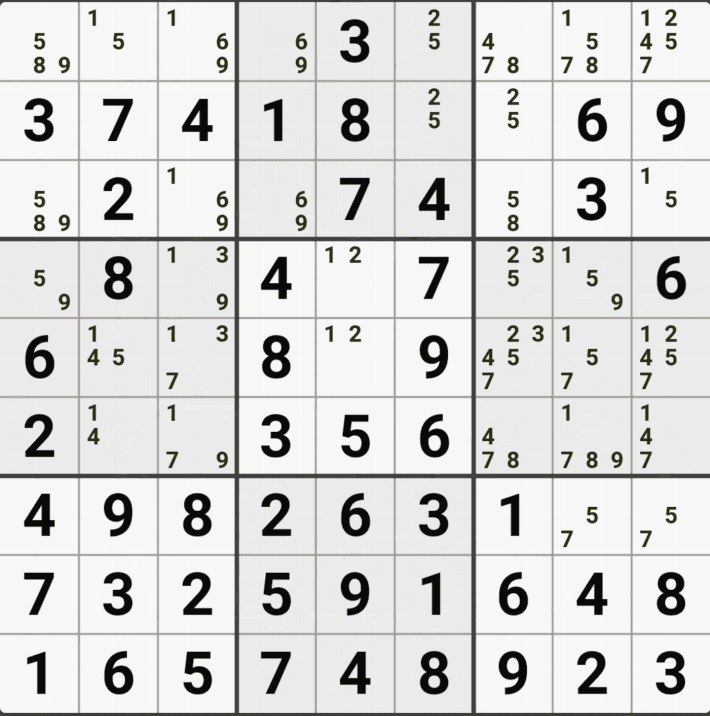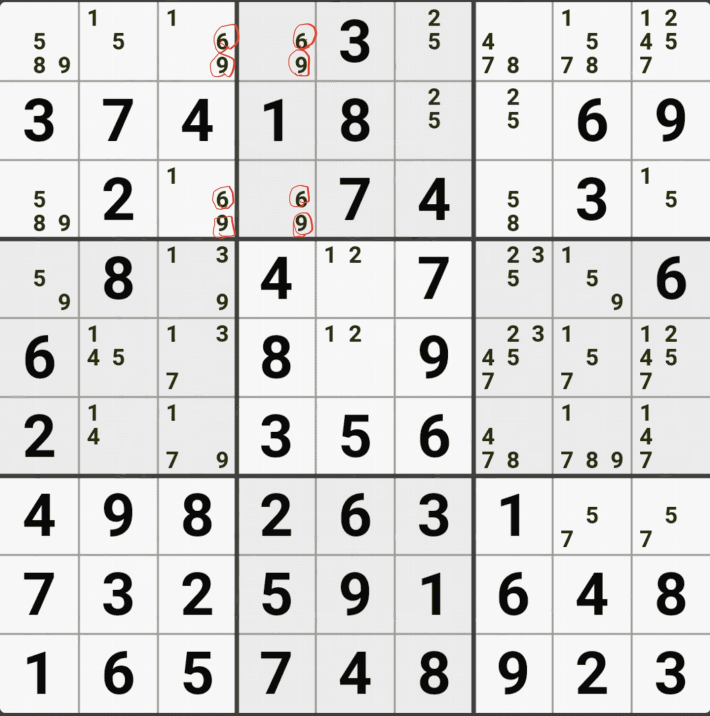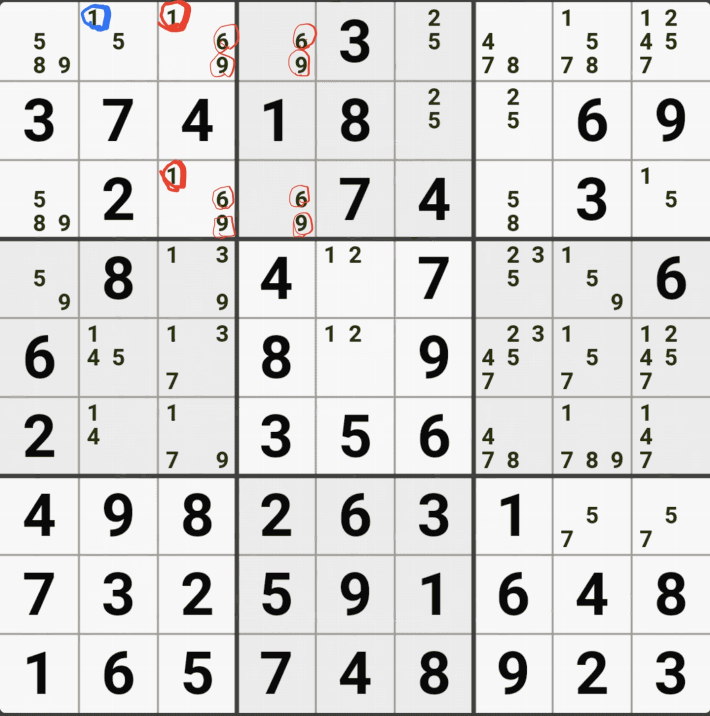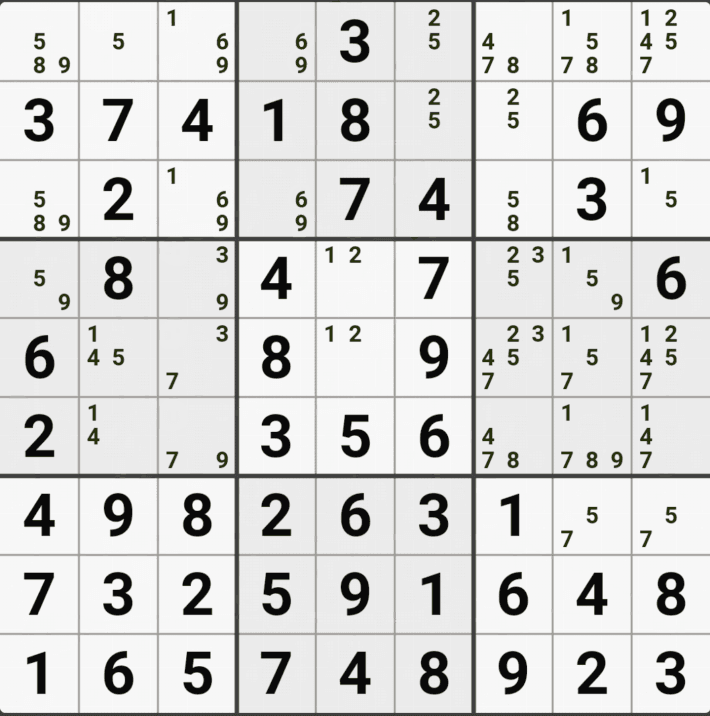
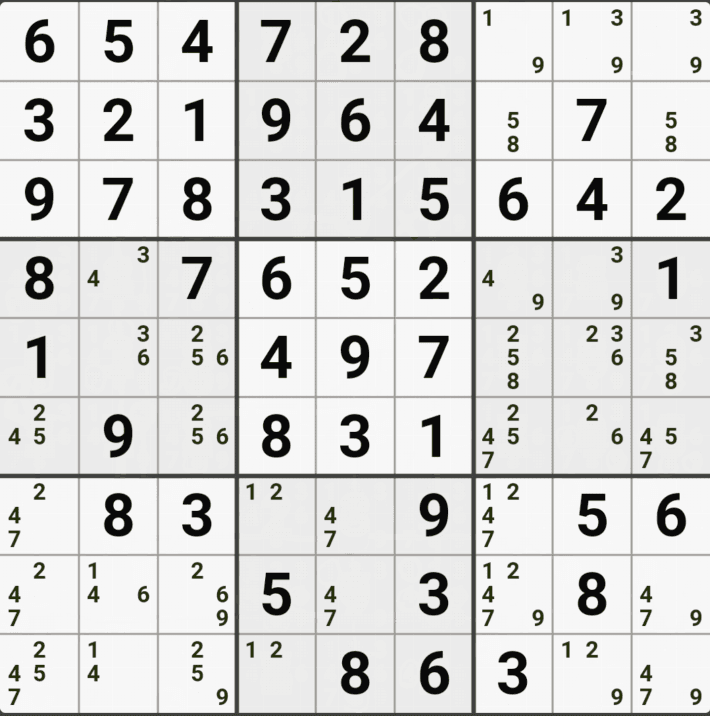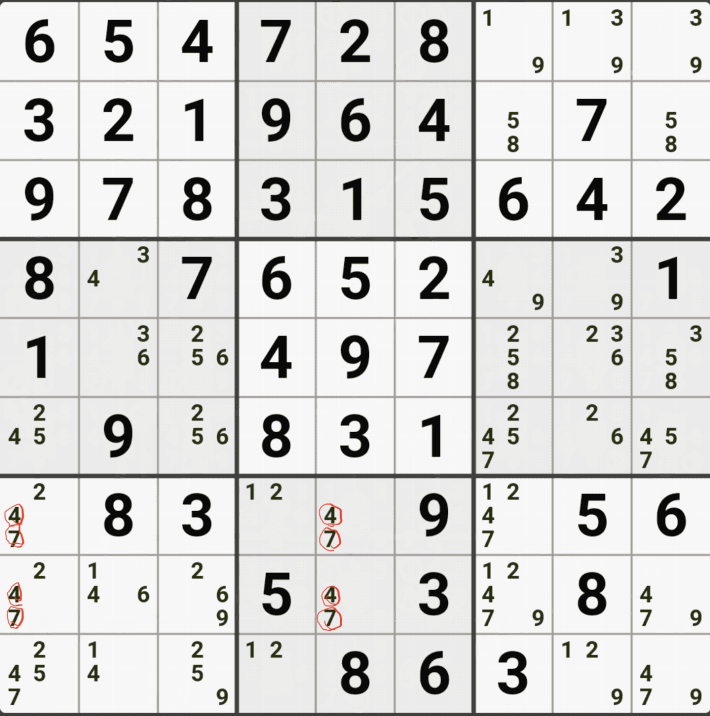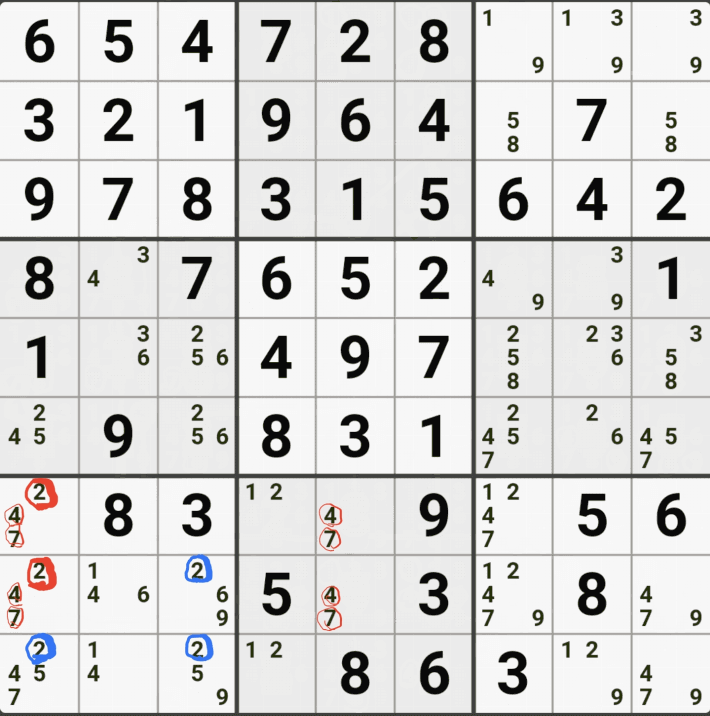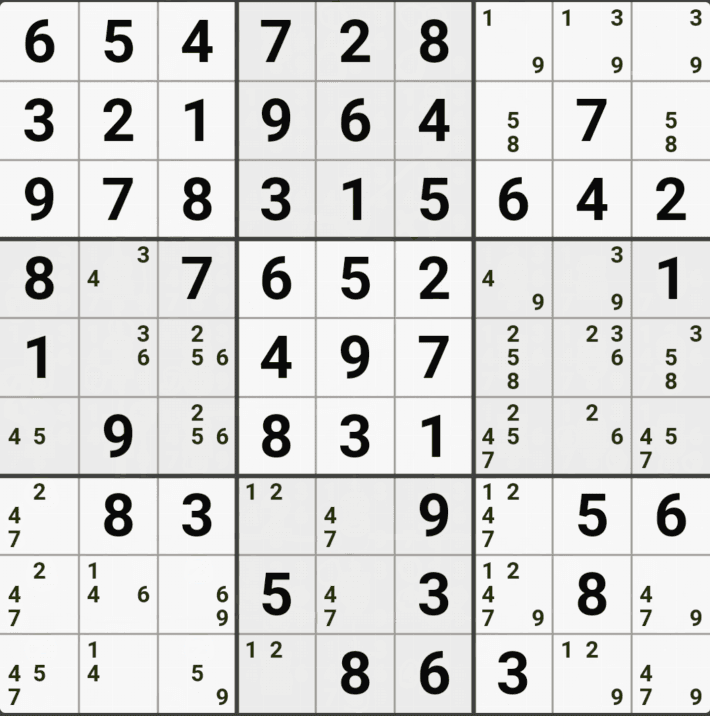
아래는 위의 움짤1. 과 같은 개념인데 위치와 숫자의 갯수만 더 넣어봤다. 쭉쭉 보자~
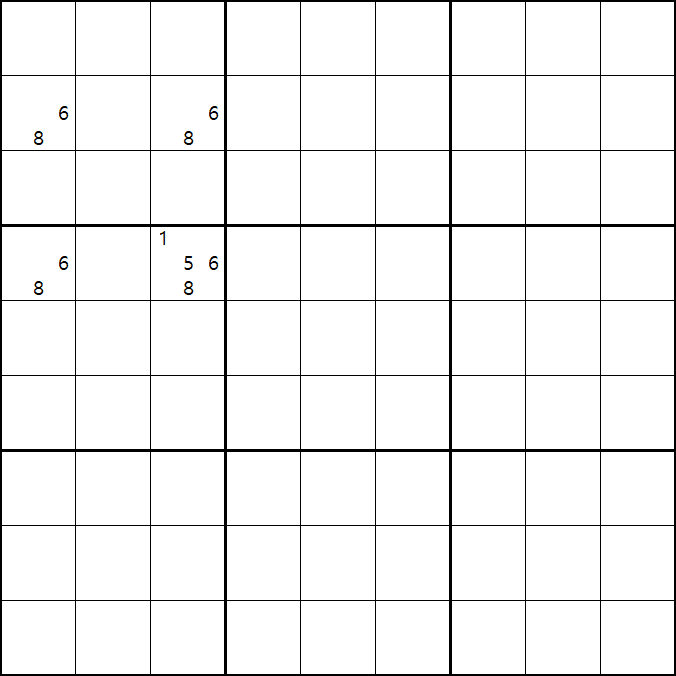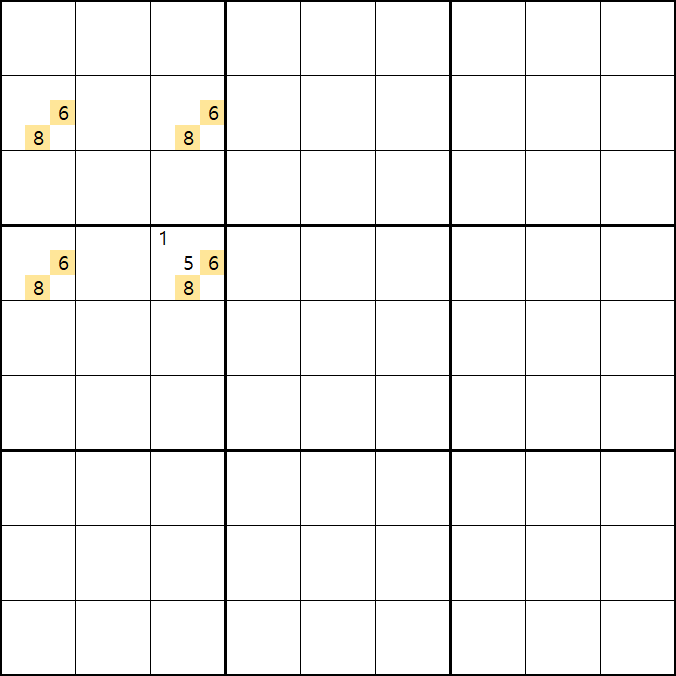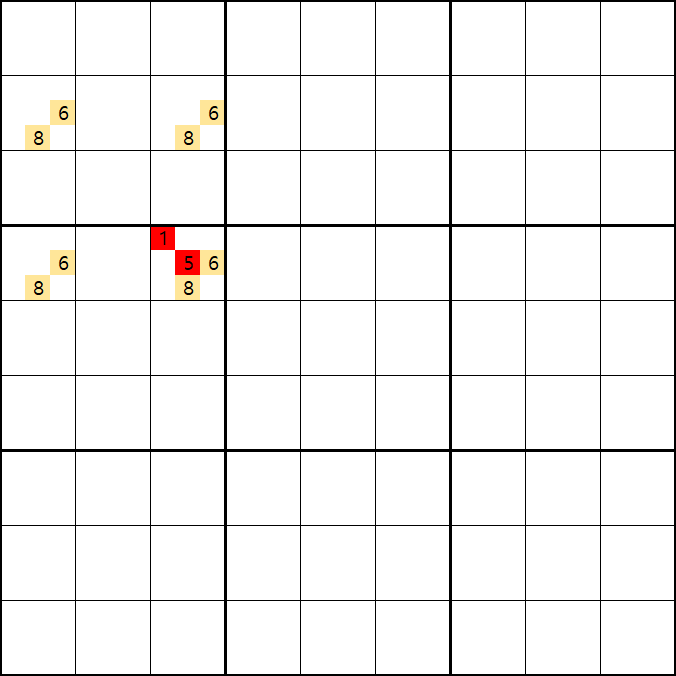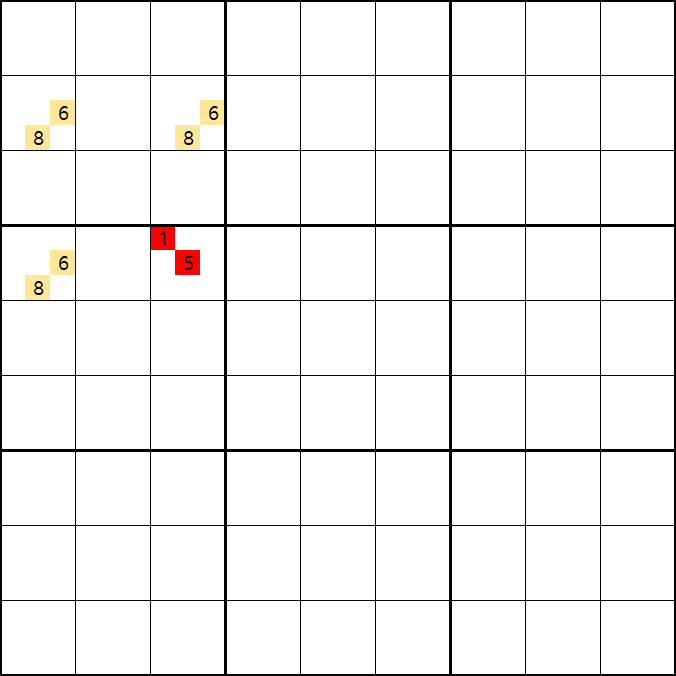
위의 움짤과 같이 사각형을 이루는 4개의 칸에 6/8[B1], 6/8[B3] , 6/8[D1], 1/5/6/8 [D3]에 존재할 때,
D3에 6또는 8이 들어가면 답이 2개가 되는 모순된 상황이 생기게 되므로
모순된 상황을 제거 하기 위해서 6[D3]과 8[D3]을 제거할 수 있다. 즉, D3에는 반드시 1또는 5중 1개의 후보숫자가 들어가야만 한다.
위의 움짤과 같이 사각형을 이루는 4개의 칸에 6/8[B1], 6/8[B3] , 1/5/6/8/9[D1], 6/8[D3]에 존재할 때,
D1에 6또는 8이 들어가면 답이 2개가 되는 모순된 상황이 생기게 되므로
모순된 상황을 제거 하기 위해서 6[D1]과 8[D1]을 제거할 수 있다. 즉, D3에는 반드시 1,5,9 중의 1개의 후보숫자가 들어가야만 한다.
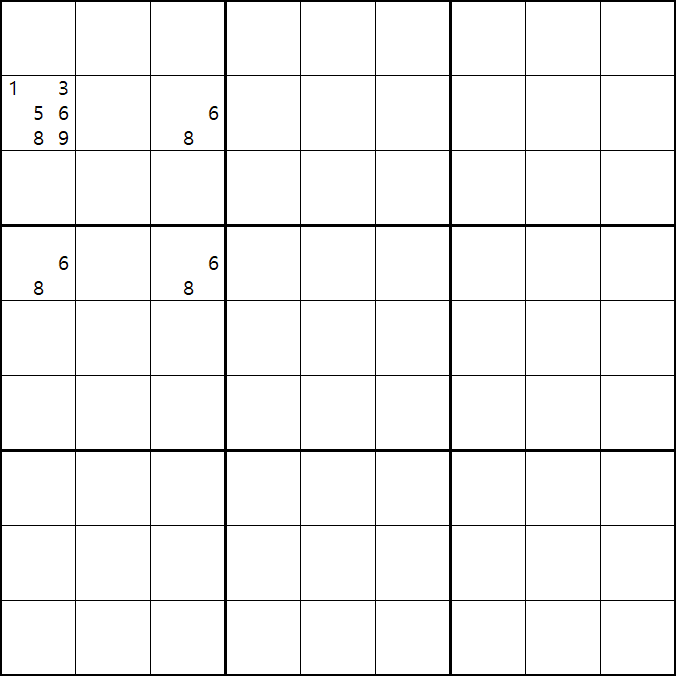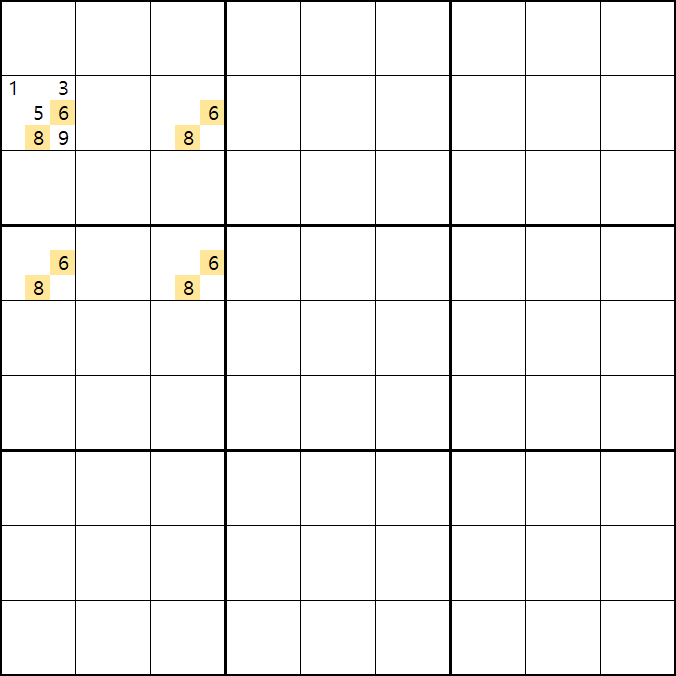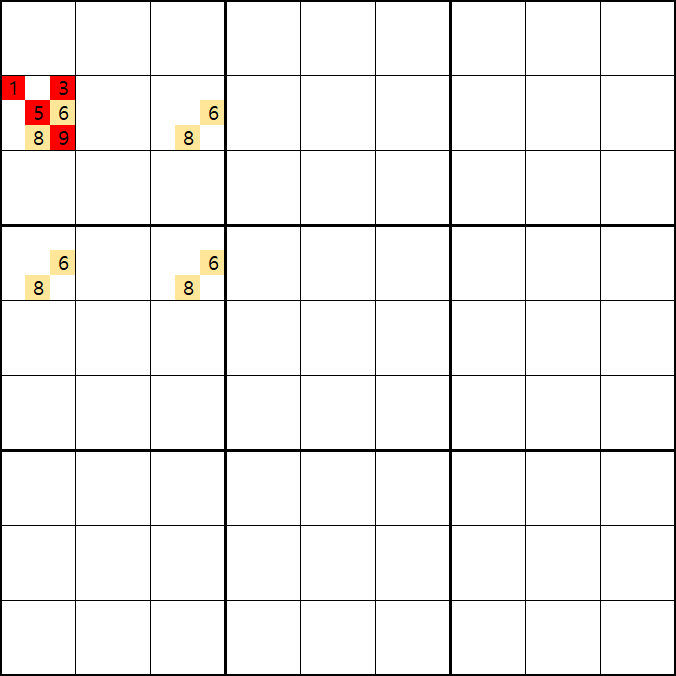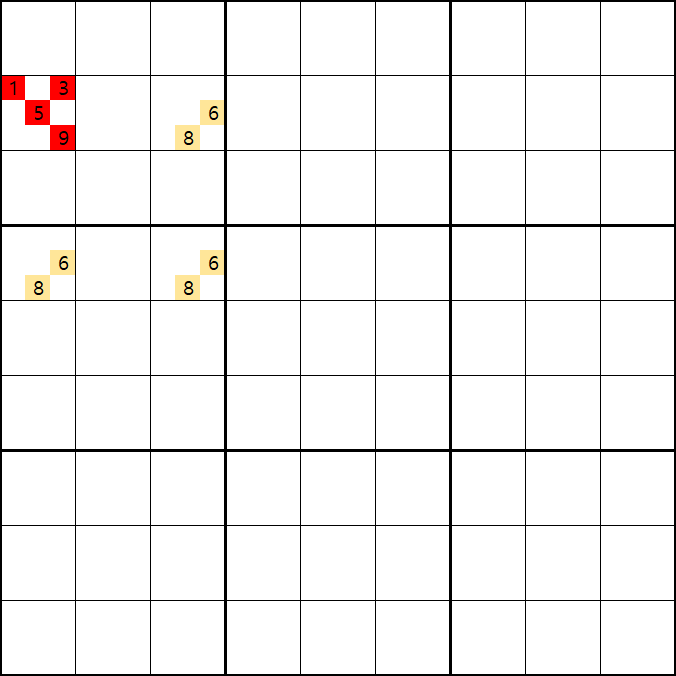
위의 움짤과 같이 사각형을 이루는 4개의 칸에 1/3/5/6/8/9[B1], 6/8[B3] , 6/8[D1], 6/8[D3]에 존재할 때,
B1에 6또는 8이 들어가면 답이 2개가 되는 모순된 상황이 생기게 되므로
모순된 상황을 제거 하기 위해서 6[D1]과 8[D1]을 제거할 수 있다. 즉, D3에는 반드시 1,3,5,9 중 1개의 숫자가 들어가야만 한다.
유니크 렉탱글 Type 2A - 처음에 본 숫자 8 - 6개를 한 번에 지운 공식
Floor : XY / XY
Roof : XYZ / XYZ 형태
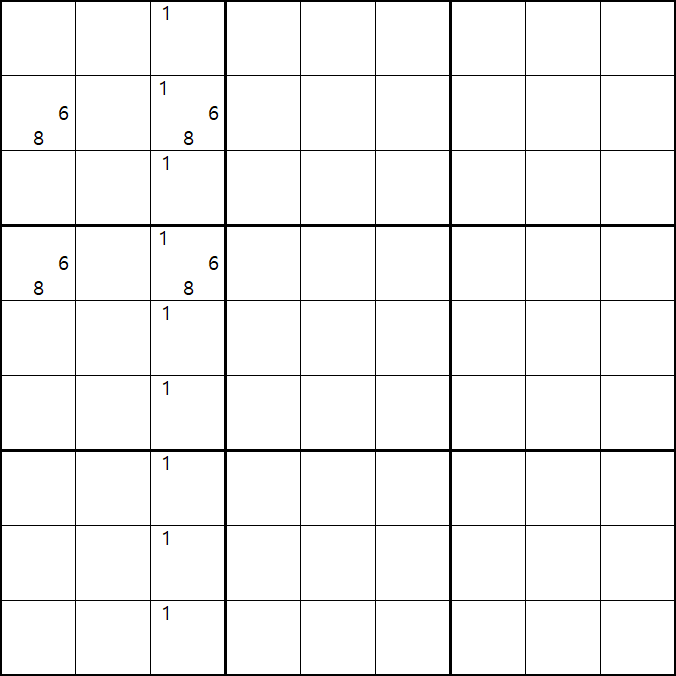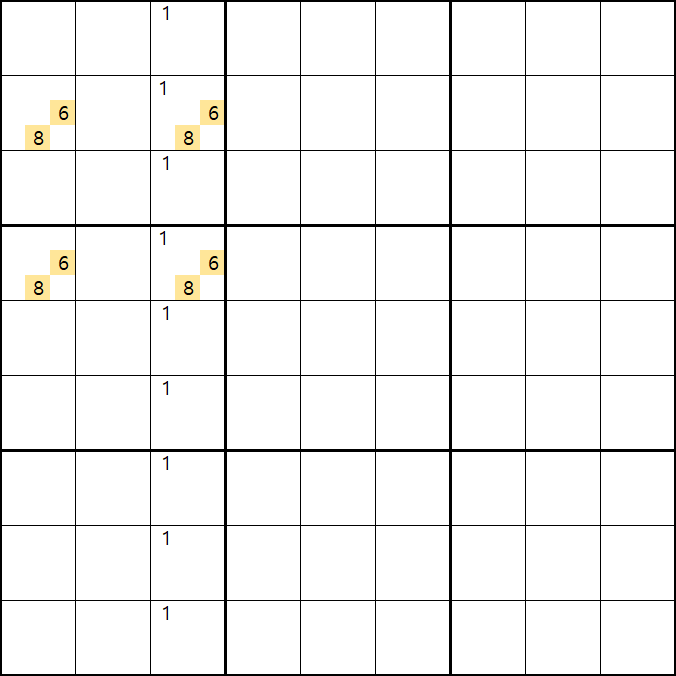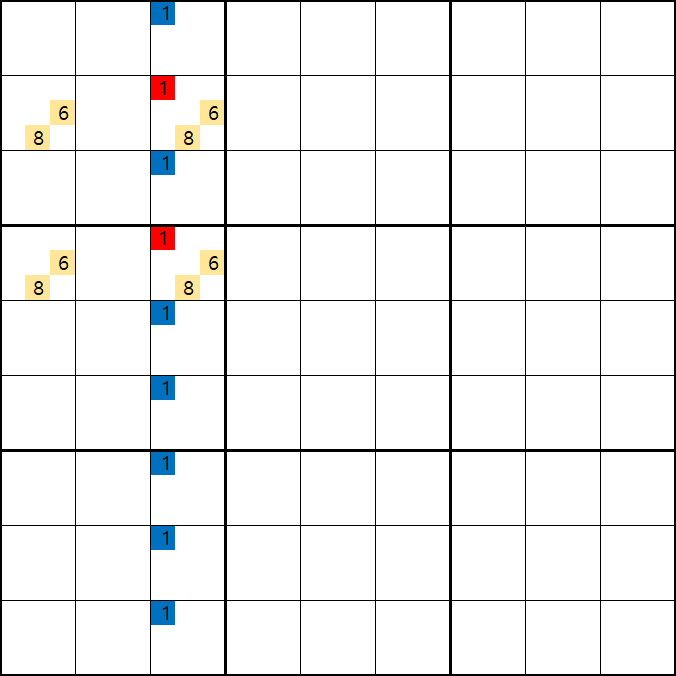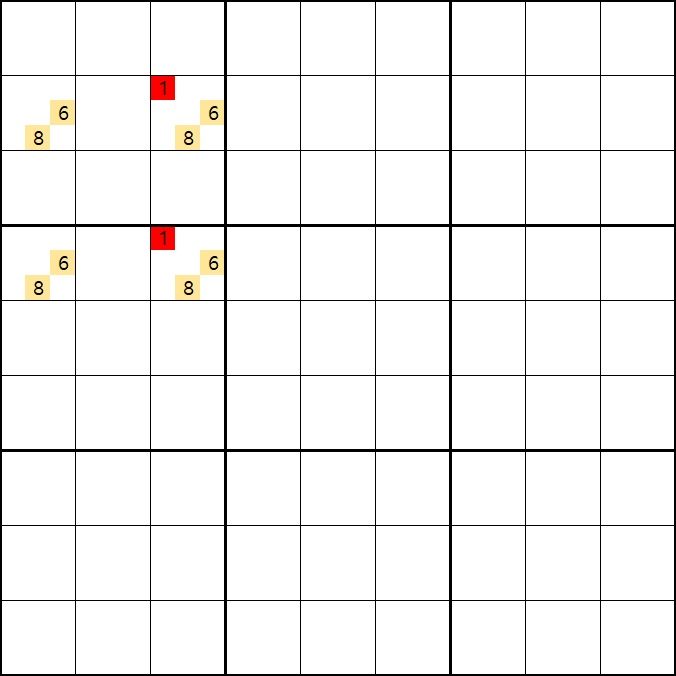
위의 움짤과 같이 사각형을 이루는 4개의 칸에 6/8[B1], 1/6/8[B3] , 6/8[D1], 1/6/8[D3]에 존재할 때,
B3 또는 D3에 6또는 8이 들어가면 답이 2개가 되는 모순된 상황이 생기게 되므로
모순된 상황을 제거 하기 위해서는 1[B3] 또는 1[D3] 중 한칸에는 반드시 1이 들어가야 된다.
따라서 B3과 D3을 제외한 3열에 있는 모든 후보숫자 1을 제거할 수 있다. (확실한 페어와 같은 효과)

위의 움짤과 같이 사각형을 이루는 4개의 칸에 1/6/8[B1], 1/6/8[B3] , 6/8[D1], 6/8[D3]에 존재할 때,
B1 또는 B3에 6또는 8이 들어가면 답이 2개가 되는 모순된 상황이 생기게 되므로
모순된 상황을 제거 하기 위해서는 1[B1] 또는 1[B3] 중 한칸에는 반드시 1이 들어가야 된다.
따라서 B1과 B3을 제외한 박스1에 있는 후보숫자 1과, B행에 있는 후보숫자 1을 모두 제거할 수 있다. (페어제거와 같은 효과)
유니크 렉탱글 Type 2C - 플로어와 루프에 XY / XYZ 가 엇갈려 있는 경우
Floor : XYZ / XY
Roof : XY / XYZ 형태
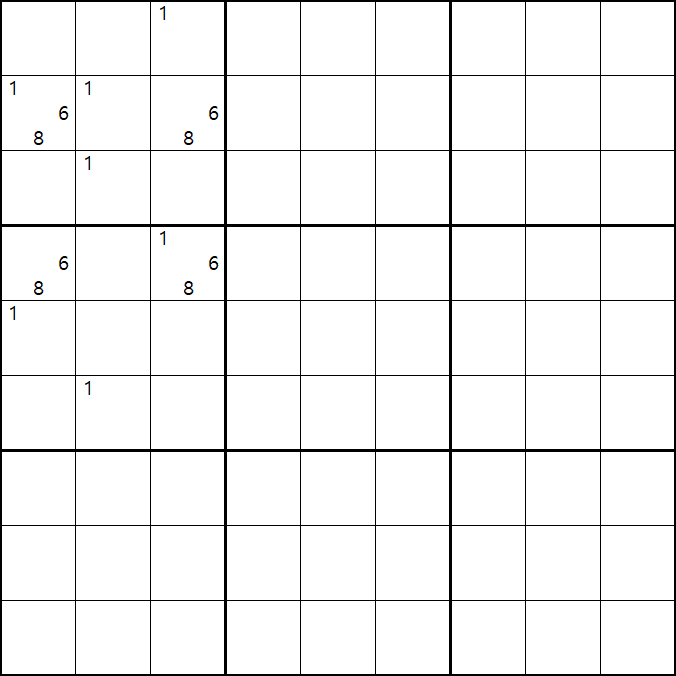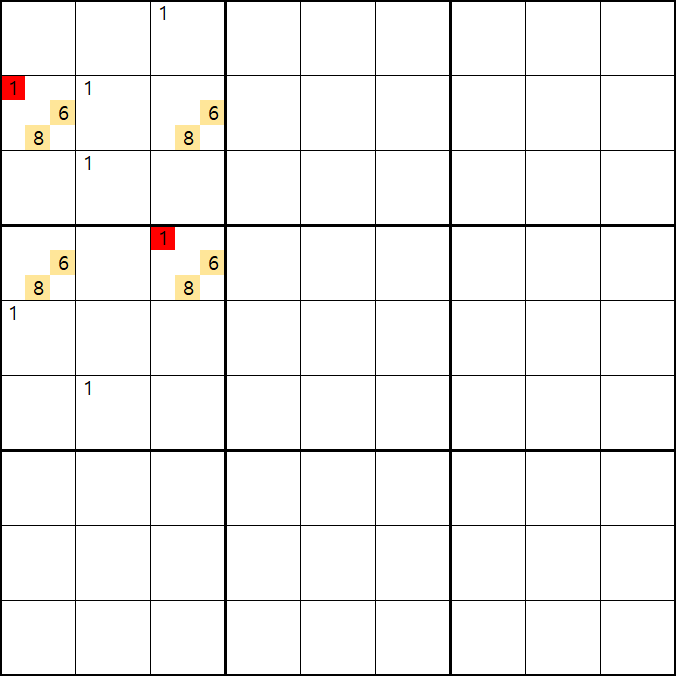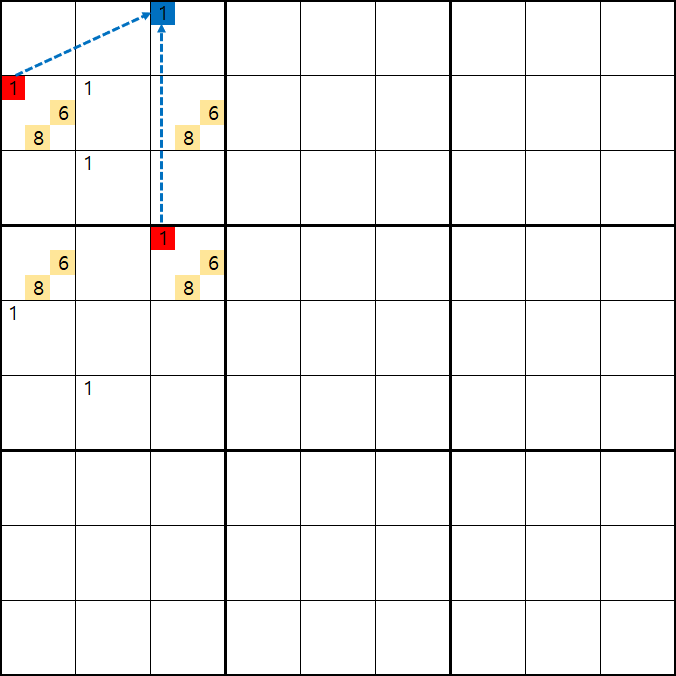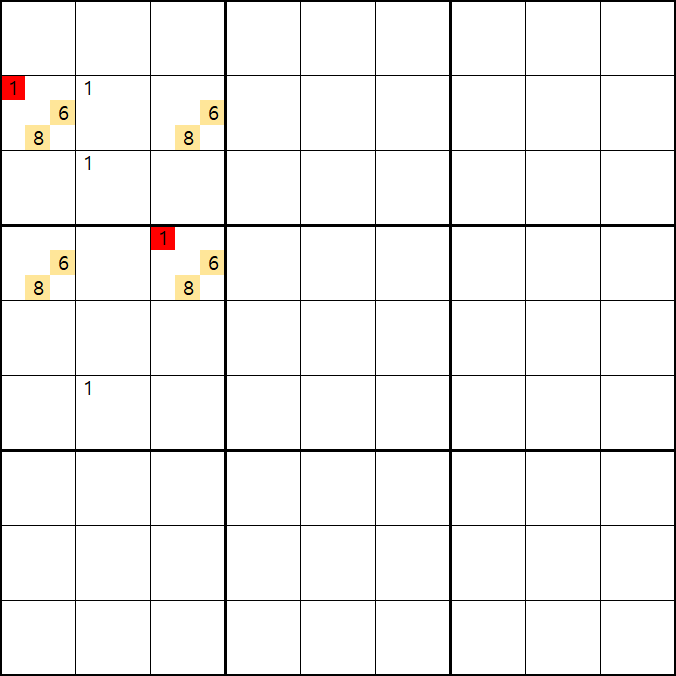
위의 움짤과 같이 사각형을 이루는 4개의 칸에 1/6/8[B1], 6/8[B3] , 6/8[D1], 1/6/8[D3]에 존재할 때,
B1 또는 D3에 6또는 8이 들어가면 답이 2개가 되는 모순된 상황이 생기게 되므로
모순된 상황을 제거 하기 위해서는 1[B1] 또는 1[D3] 중 한칸에는 반드시 1이 들어가야 된다.
따라서 1[B1] 과1[D3] 이 서로 마주보는(=교차되는) 1[A3]과 1[E1] 2개의 후보숫자를 제거할 수 있다. (XY윙과 같은 효과)
유니크 렉탱글 Type 2B - 플로어와 루프의 중간에 박스가 존재할 때 (조금은 복잡하고 위에서 본 2A 및 2C의 형태 모두 나타난다. 다만 중간에 박스가 한 개 더 존재할 뿐~이다.)
굳이 나눌 필요가 있나 싶겠지만 위의 2개의 예만 보면 아래의 모양은 잘 안 보일 수도 있고, 선구자들이 나눴기 때문에 따라간다.
Floor : XY / XYZ
빈박스
Roof : XY / XYZ 형태
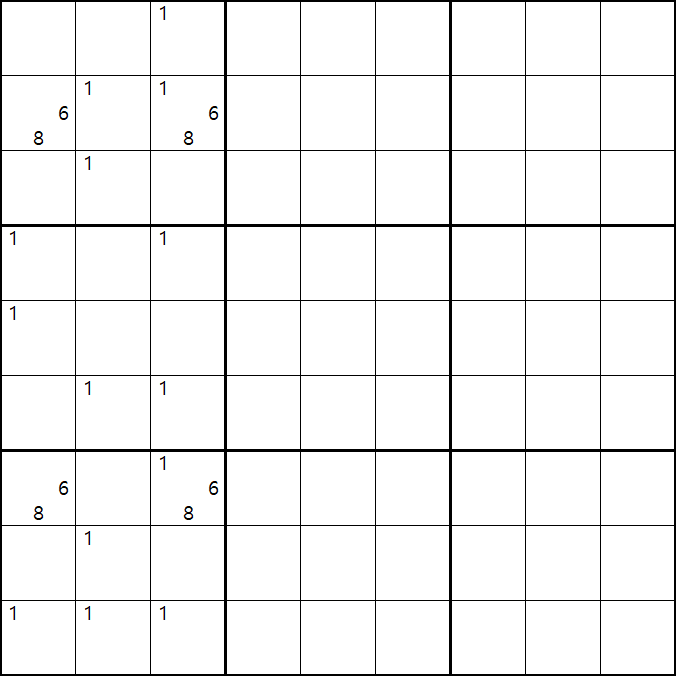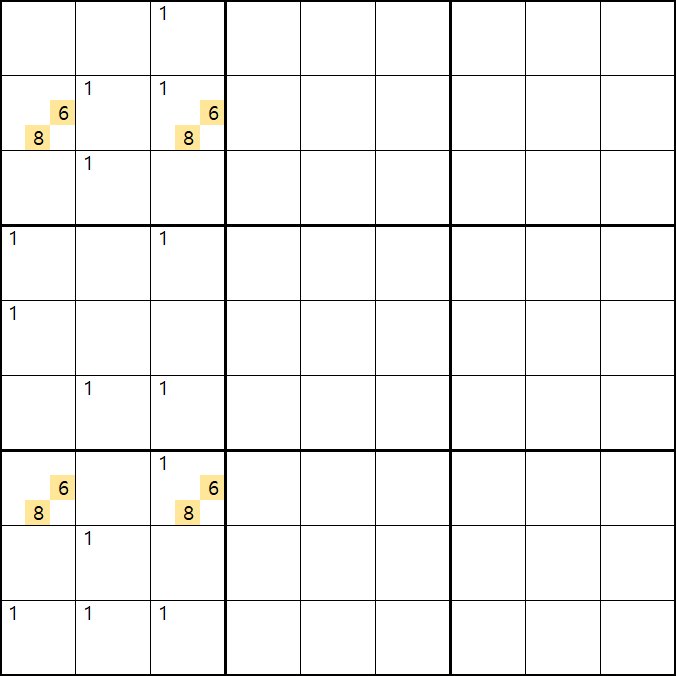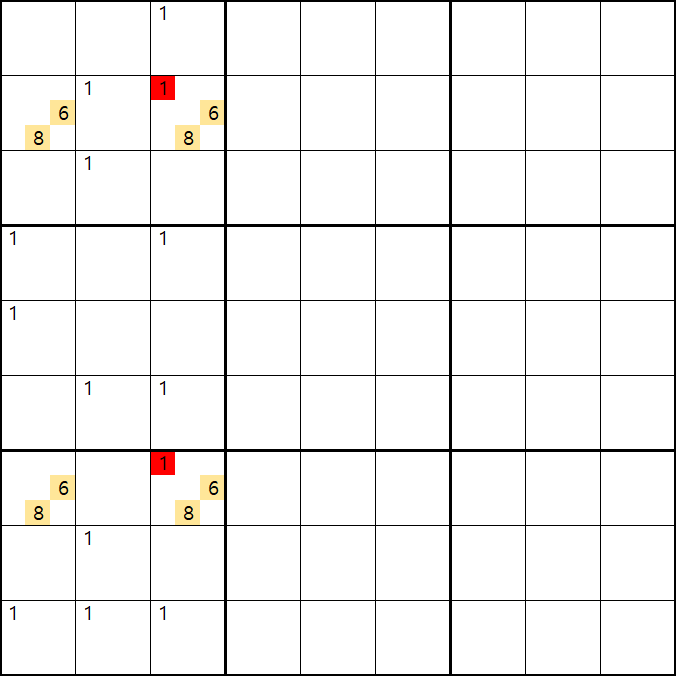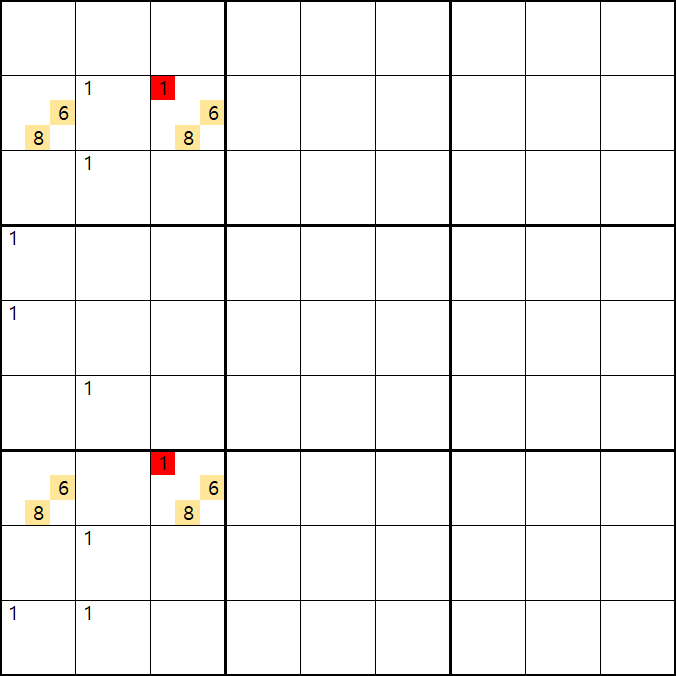
위의 움짤과 같이 사각형을 이루는 4개의 칸에 6/8[B1], 1/6/8[B3] , 6/8[G1], 1/6/8[G3]에 존재할 때,
B3 또는 G3에 6또는 8이 들어가면 답이 2개가 되는 모순된 상황이 생기게 되므로
모순된 상황을 제거 하기 위해서는 1[B3] 또는 1[G3] 중 한칸에는 반드시 1이 들어가야 된다.
따라서 B3과 G3을 제외한 3열에 있는 모든 후보숫자 1을 제거할 수 있다. (확실한 페어와 같은 효과)
자 이정도면 여러 스도커도 유니크 렉탱글에 대한 개념은 잡았을 거라 본다. 그런데, 스도쿠를 조금 했던 스도커라면 위의 움짤 예제를 보고 이런 생각이 들 것이다.
XY 이중링크에 더해서 XYZ의 형태를 이루는데, XYZ를 초과하는 형태도 있지 않을까? 라는 생각 말이다.
물론 있다.
그런데 그런 형태는 위에서 말한대로 Type3~Type5에 루프에 이중링크외에 후보숫자가 2~4개, 또는 확실한 트리플과 연계, XY/XY/XYZ/XYW 형태 등이 있는데... 아직 내가 개념을 이해하지 못했다. 빨리 이해해 보고 파트 2를 써보도록 하겠지만 위의 Type1, 2만 잘 익혀도 큰 힘을 낼 수 있다.
아래는 실전예제인데 많지는 않지만 유니크 렉탱글을 정확히 이해하는데 도움이 될 거라 믿는다. 여러번 보고 꼭 익히자~
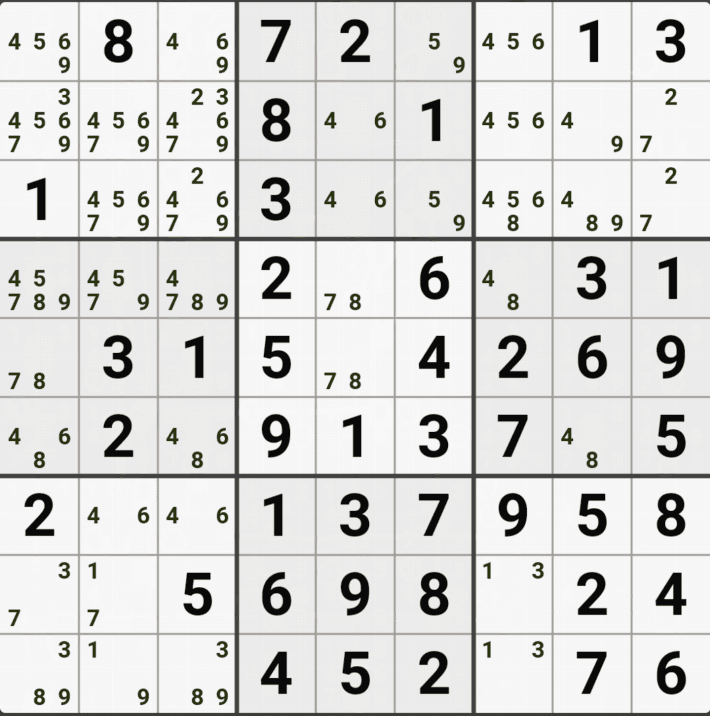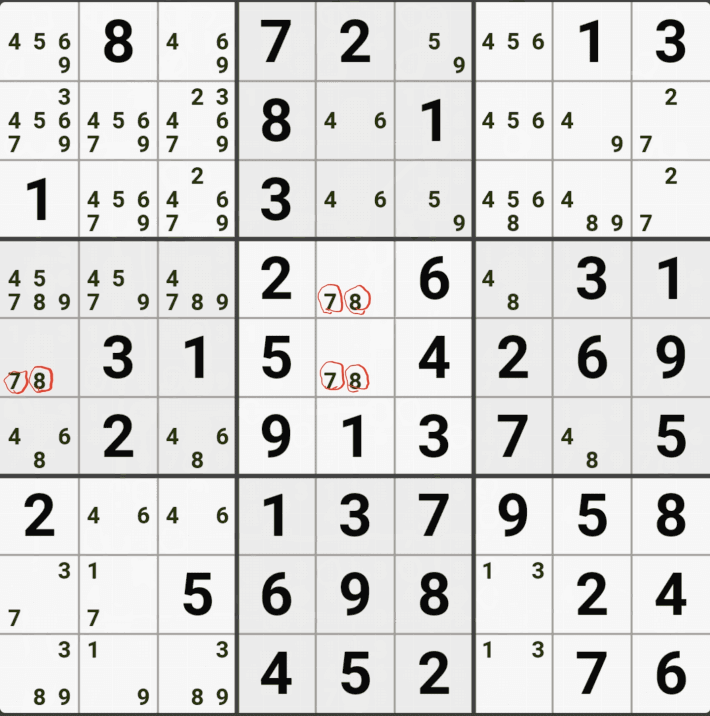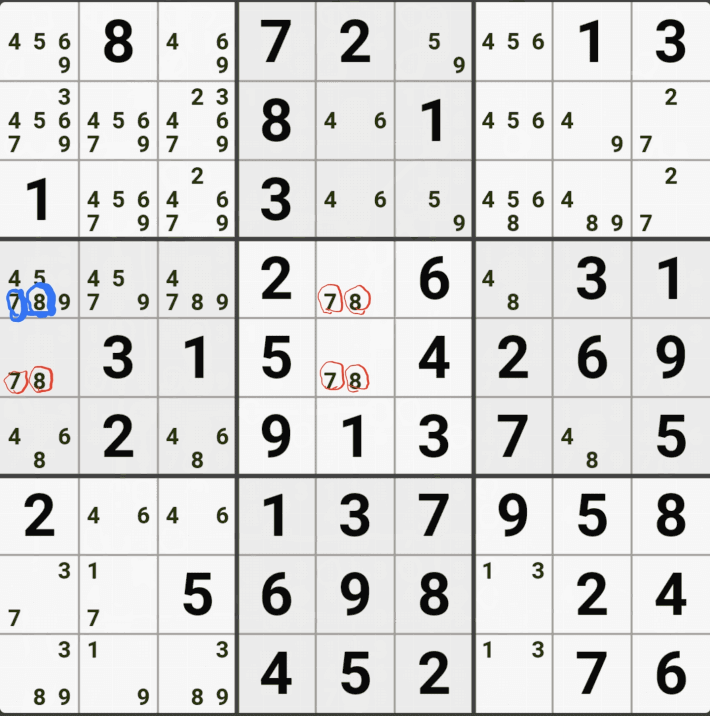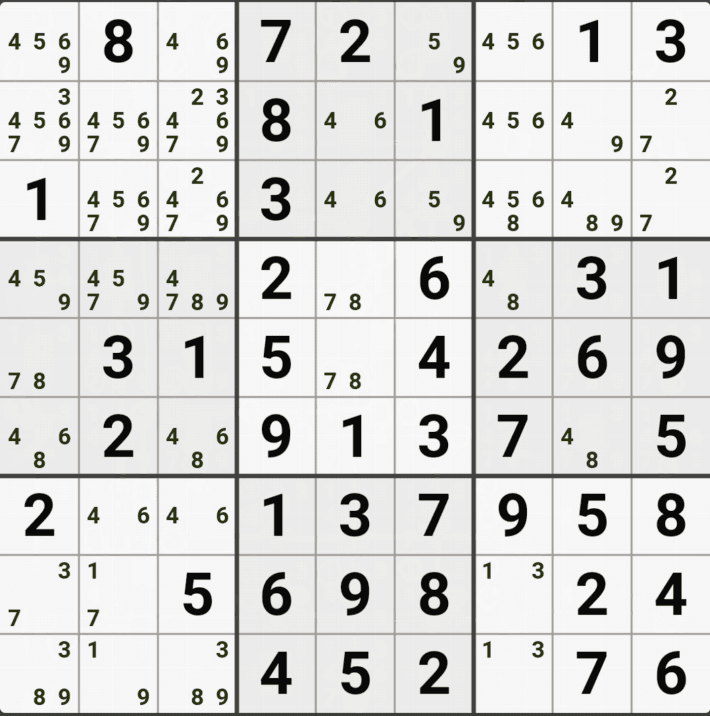
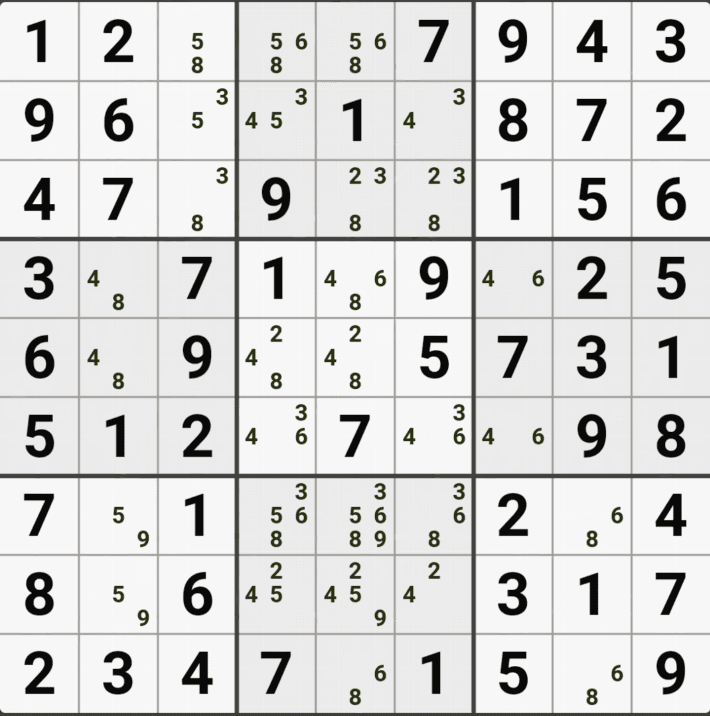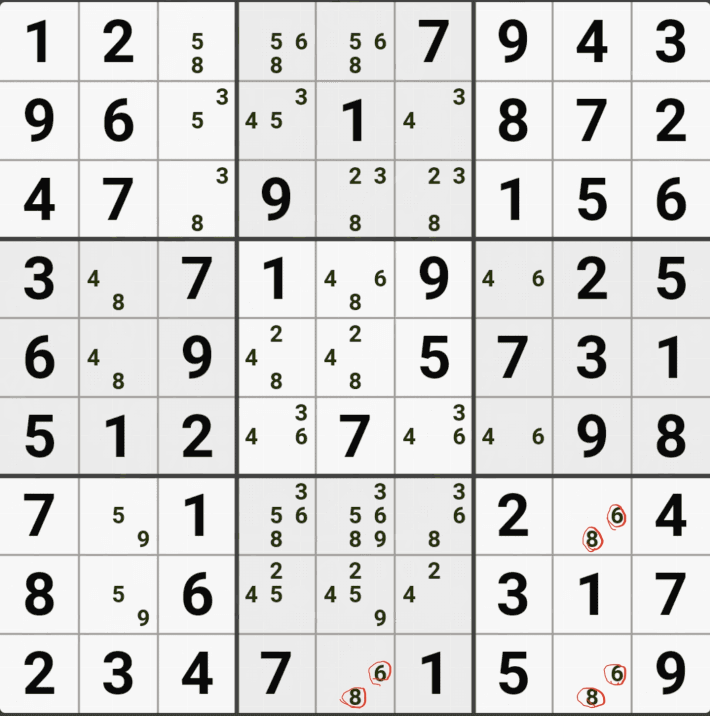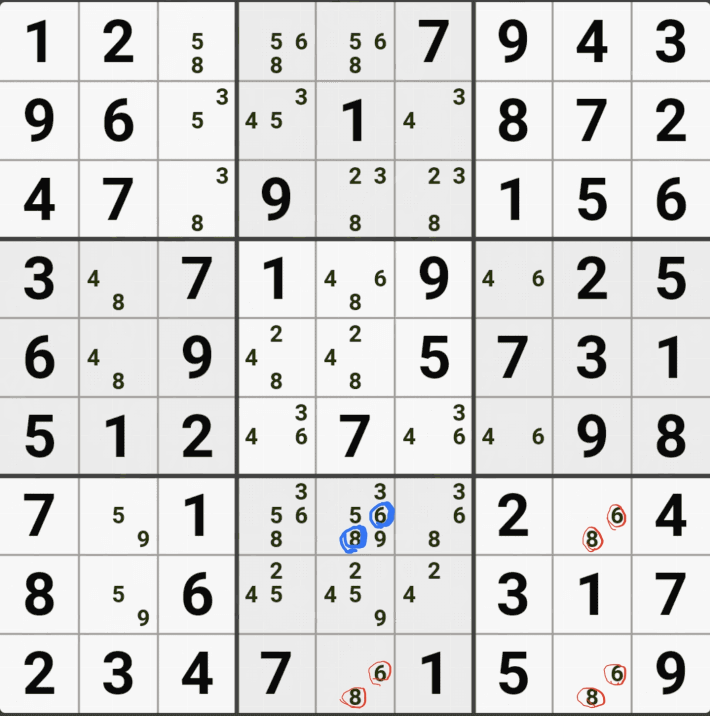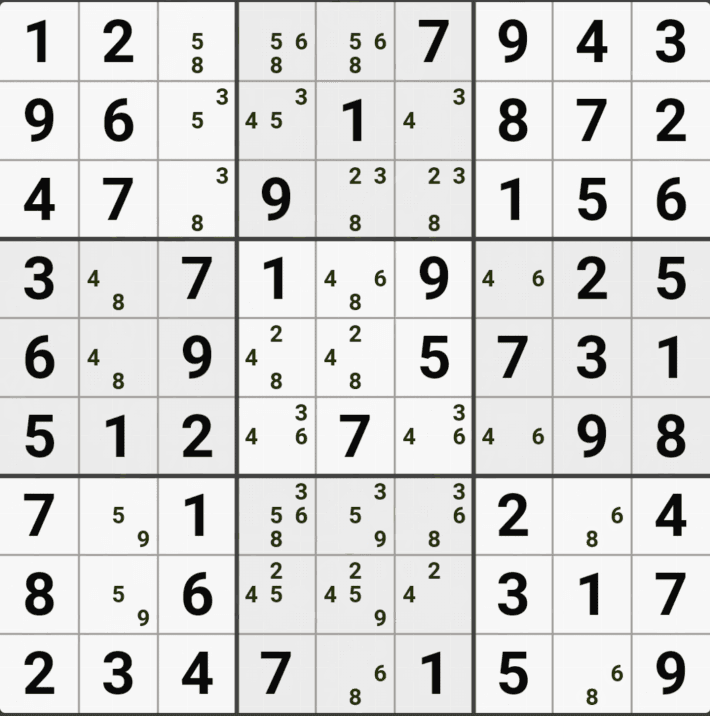
유니크 렉탱글 Type 1 실전 예제 (5개)

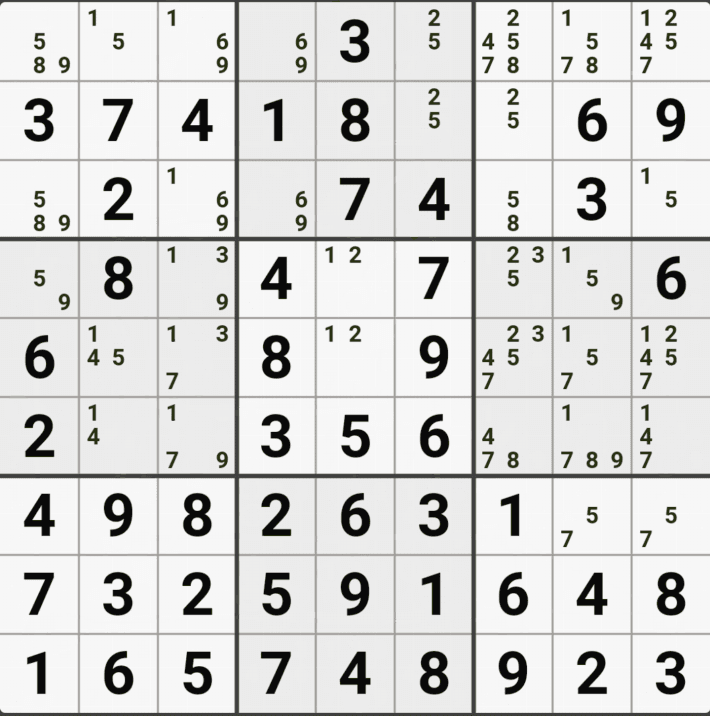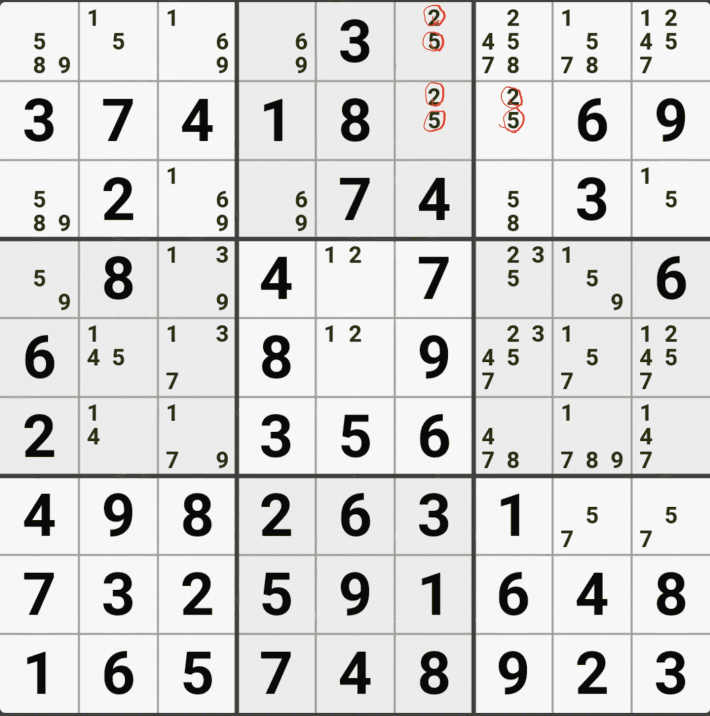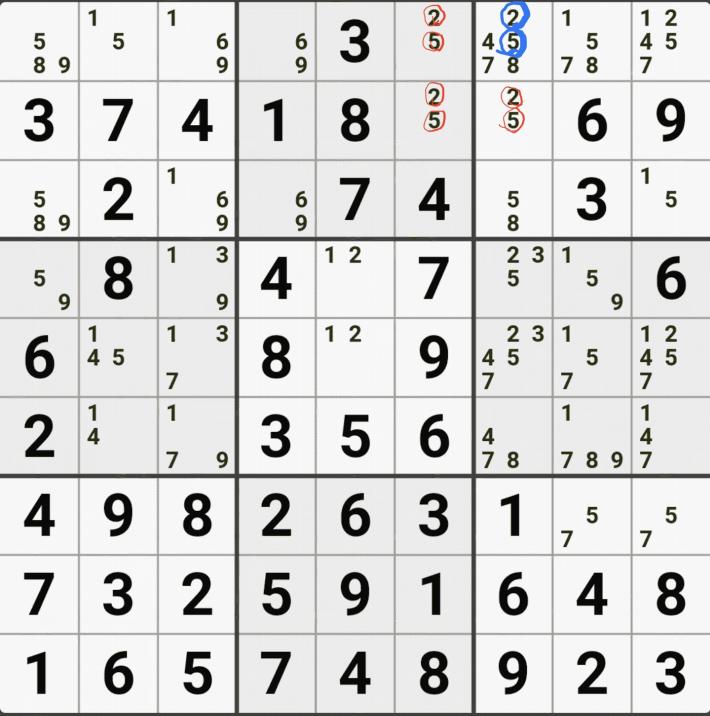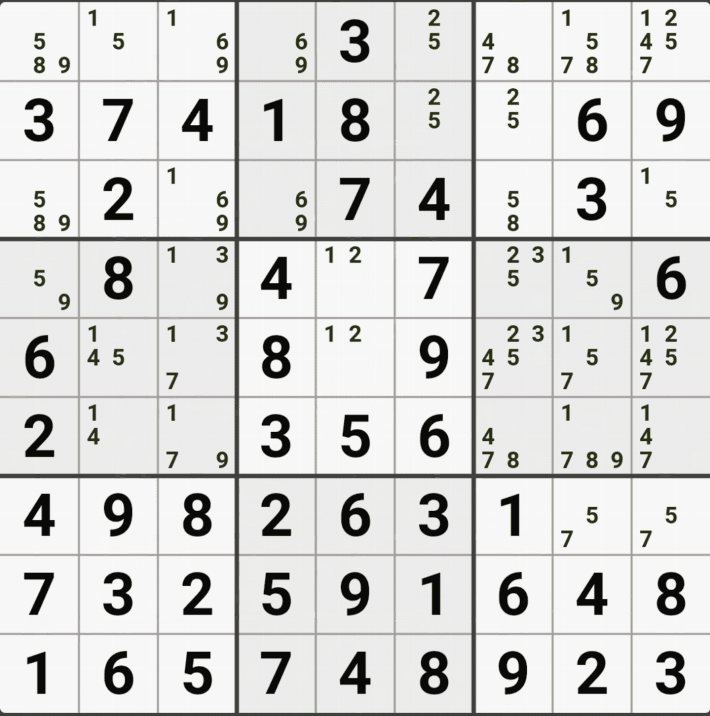
유니크 렉탱글 Type 2 실전 예제 (7개)



움짤로 익히는 스도쿠 9. 유니크 렉탱글 Part 2.(Type3)
움짤로 익히는 스도쿠 9. 유니크 렉탱글 Part 2.(Type3)
이번 글에서는 지난 번 글 움짤로 익히는 스도쿠 8. 유니크 렉탱글(Unique Rectangles) Part 1. 에서 익힌 기본적인 형태에서 좀 더 변형된 페어 및 트리플 형태가 추가되는 '유니크 렉탱글 Type 3' 에 대
inoks.tistory.com
움짤로 익히는 스도쿠 10. 유니크 렉탱글 Part 3.(Type4,5)
움짤로 익히는 스도쿠 10. (히든) 유니크 렉탱글 Part 3.(Type4,5)
이번 글에서는 지난 글에서 알아본 유니크 렉탱글 Type 1, 2, 3에 이어서 4,5에 대한 글을 쓰려고 한다.(드디어 이해를 했다.) 일단, 이 글은 유니크 렉탱글 Type1에 대한 개념은 알고 있는 스도커를 타
inoks.tistory.com