스도쿠 17. 고급공식/ 사각형 제거-움짤, 패턴

 이번 글에서는 비교적 최근인 2023년 하반기에 공식화된 사각형 제거(Rectangel Elimination)에 대해 알아 보도록 하겠다. 개념이 좀 생소한 증명이 나오게 되는데, 이해가 안되는 사람이 있다면 유용한 전략이니까 공식만 알아놔도 좋을 거 같다. X윙, 222 소드 피쉬 X 사이클을 정형화 시킨 형태에 이름을 붙인 것인데, 사각형 제거 또한 간단한 그룹 X 사이클의 특정한 상황을 이름 붙여서 공식처럼 써 먹는 것이다. 

 

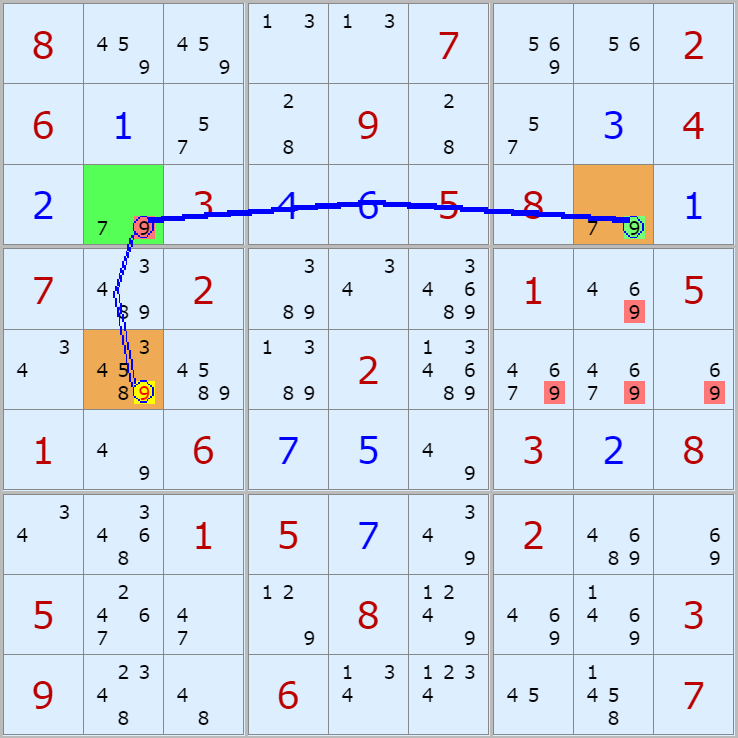
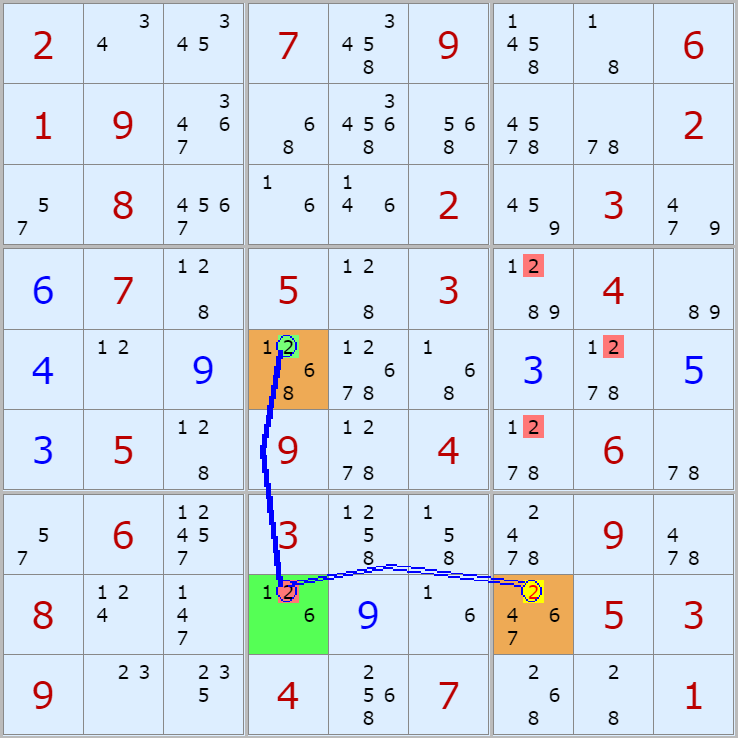
우선 아래의 움짤 예제를 보고 사각형 제거의 개념을 익히자. 

 

 

 일단 형태는 우리가 잘 알고 있는 Y윙의 형태를 닮았다. 그런데 한 가지 다른 점은 시작점과 끝점이 마주 보는 (1,6)의 후보수9가 아닌 체인의 끝점(1,2)의 후보수 9가 지워진다는 것이다. 

 

 즉, 사각형 제거는 후보숫자 X의 시작점과 끝점을 2개를 L 자 형태로 체인을 만들 때, 

 시작되는 링크는 스트롱 링크 끝나는 링크는 위크 링크로 연결 했을 때,

 크로스 되는 행과 열에 대한 시작점과 끝점 2개 모두 위크 링크로 연결된다면 

 끝점의 후보숫자 X를 제거할 수 있다.  

 

 아 말로 스도쿠 설명하는 것은 나도 이해하기 어렵고 설명하기도 참 어렵다. 움짤로 보자~

 

 위의 결과가 나오는 것을 체인의 시작점인 (7,6)이 9인 경우와 9가 아닌 경우로 나눠서 움짤로 설명해 보겠다. 

 

경우1. (7,6)칸의 확정숫자가 9라면

 

 

위의 움짤과 같이 셀2의 후보숫자 9 세 칸중에 (1,5)칸의 후보숫자 9가 확정숫자가 되며

(1,2)와 (7,2)칸의 후보숫자 9 두개는 제거된다. 

 

경우2. (7,6)칸의 확정숫자가 9가 아니라면

 

 

 

 (7,6)의 확정숫자가 9가 아니라면 

(7,2)칸의 후보숫자 9가 확정 숫자가 되고 (셀2의 후보숫자 '?' 표시된 3개의 칸 중에 하나는 반드시 9가 되어야 한다.)

(7,2)칸의 확정숫자 9에 의해 (1,2)와 (5,2) 두칸의 후보숫자 9가 제거된다. 

 

결론 : 위의 경우1과 2의 어떤 경우가 되더라도 제거 되는 후보숫자 9 는 (1,2)칸이 된다. (역시 말로는 어렵다.) 

 

위의 경우1과 경우2의 결과그림을 움짤로 빨리 엮어 보겠다. 아래 움짤을 보면 (1,2)칸의 후보숫자 9에 대한 제거 표시 X만 변함없이 자리를 지키는 것을 알 수 있다. 즉, 사각형 제거는 어떠한 상황에서도 시작점과 끝점이 타겟점과 위크 링크로 연결이 되면 끝점의 후보숫자 X를 제거할 수 있다. 

 

 

처음의 본 움짤 예제의 결과 다이아그램을 올려 보면 아래와 같다. 

 

사각형 제거를 이제 간단히 요약해 보겠다. 

 

사각형 제거 공식 -

스트롱 링크인 시작점과  위크 링크인 끝점과 크로스 되는 타겟점에

두 점 모두 위크로 연결 되면

끝점의 후보숫자 X를 지울 수 있다. 

 

 

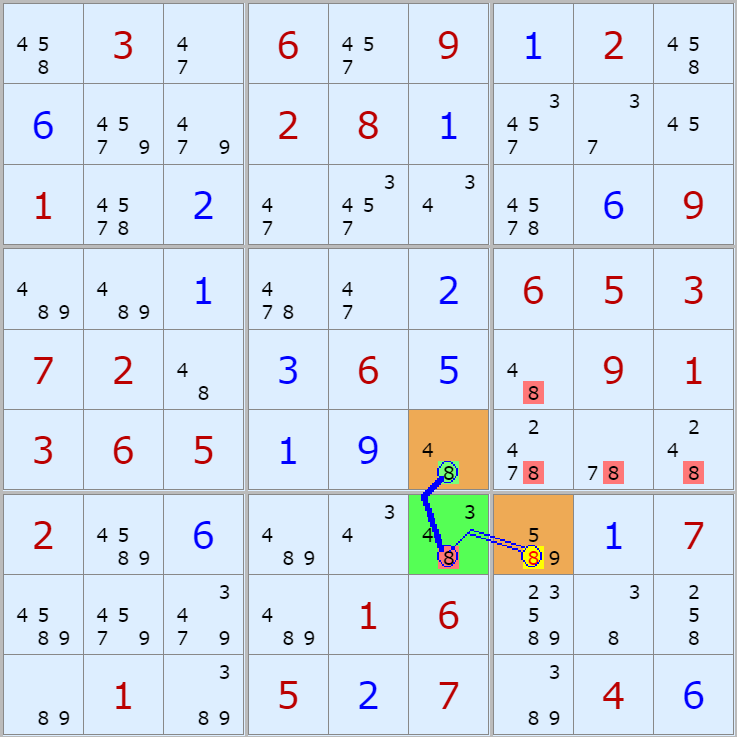
단 주의 할 점은 끝점이 아래와 같이 스트롱 링크가 된다면 시작점과 끝점 모두 후보숫자 X가 제거된다. 이를 다이아그램으로만 나타내면

 

 

위와 같은 형태로 나타나는데, 듣도보도 못한 상황이 될 수도 있음을 안다. 나도 이해 하는데 좀 걸렸다. 

 

다른 체인 기술에서도 통용되기에 시간이 걸리긴 하지만(ㅜㅜ) 이런 새로운 개념은 확실히 이해해야 나중에 잘 이해하고 써 먹을 수 있어서 증명해 보겠다. 

 

경우1. (7,6)의 후보숫자 9가 확정숫자가 아니라면

 

(7,6)의 후보숫자 9가 확정숫자가 아니라면 (이미 제거)

(7,2)의 후보숫자 9가 확정숫자가 되며 (1,2)의 후보숫자 9는 제거 된다.

즉 (1,2)와 (7,6)의 후보숫자 9 제거됨.

 

다만 셀2에 존재하는 후보숫자 9 세칸은 특정할 수 없다. 

 

경우2. (7,6)의 후보숫자 9가 확정숫자가 된다면

 

 

시작점 (7,6)의 후보숫자 9가 확정숫자가 된다면 (1,5)의 후보숫자 9 또한 무조건 확정숫자가 되야 한다. 

그러면 동시에 끝점(1,3)과 (7,2)의 후보숫자 9가 제거 되는 경우가 생긴다.

이는 같은 하우스 안에는 1~9까지 모든 숫자가 1개씩 들어 가야 한다는 스도쿠의 규칙에 위배되므로 

모순되는 경우로 존재할 수 없는 상황이기 때문에 (7,6)에는 후보수 9가 확정 될수 없다. 

 

따라서 위의 경우1의 상황만 스도쿠 규칙으로 존재할 수 있기 때문에 시작점과 끝점 모두 후보수 9가 제거된다. 

 

>>>>> 우리가 지금까지 알아온 체인 공식은 2가지의 경우의 수 모두가 같은 값을 가지는 반면에

 

'사각형 제거' 모든 연결이 스트롱 링크가 되면 위의 경우처럼

 

경우 1. 성립

경우 2. 모순

 

두 가지의 경우에 모순되는 경우의 수는 배제하고 성립되는 경우의 수만 취해서 후보수를 제거하는 방법도 있다. 

 

이러한 상황은 X사이클 '스트롱 링크형'에서도 존재한다.

 

 또한 나도 스린이로써 고급 스도쿠 공식을 이해하고 적용하려고 하면 잘 나타나지 않아서 실제로 그 공식을 써야할 때는 패턴도 달라지기 때문에 잘 보이지 않는다. 그래서 내린 결론은 고급 공식은 예제를 많이 보고 눈에 익혀야 한다~ 였고,

자료 90개(위크88개, 스트롱2개)를 다른 사이트에 찾아 올린다. 많이 보고 꼭 체득하기를 바란다. 

 

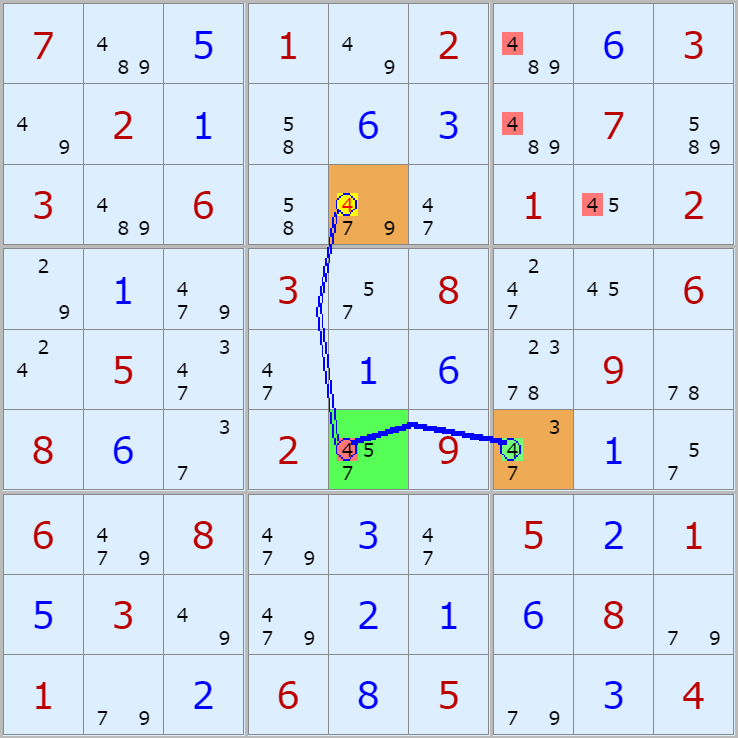
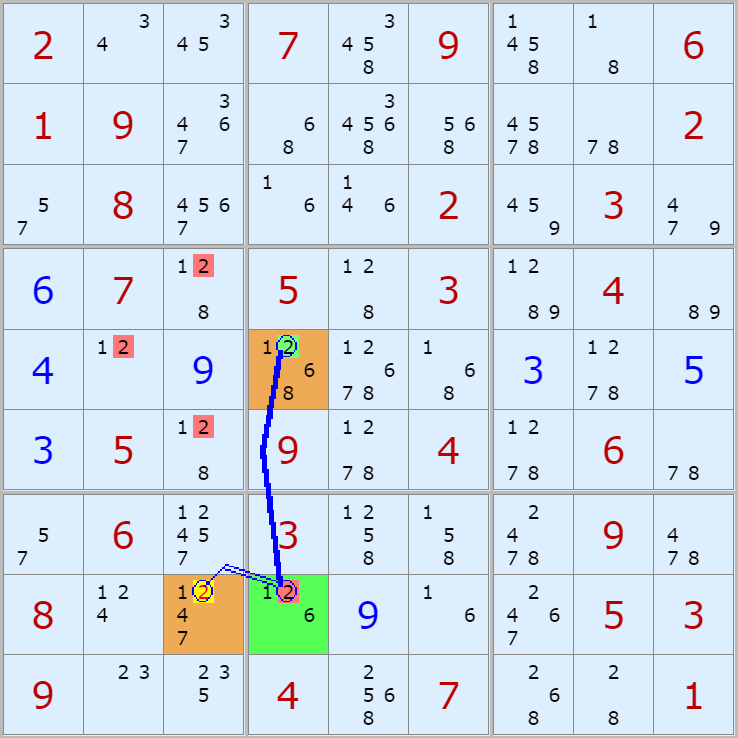
 자료의 출처는 '스도쿠 위키'라는 사이트다. 예제 자료는 아래 더 보기를 누르면 볼 수 있다. 예제는 아래와 같은 그림인데

 

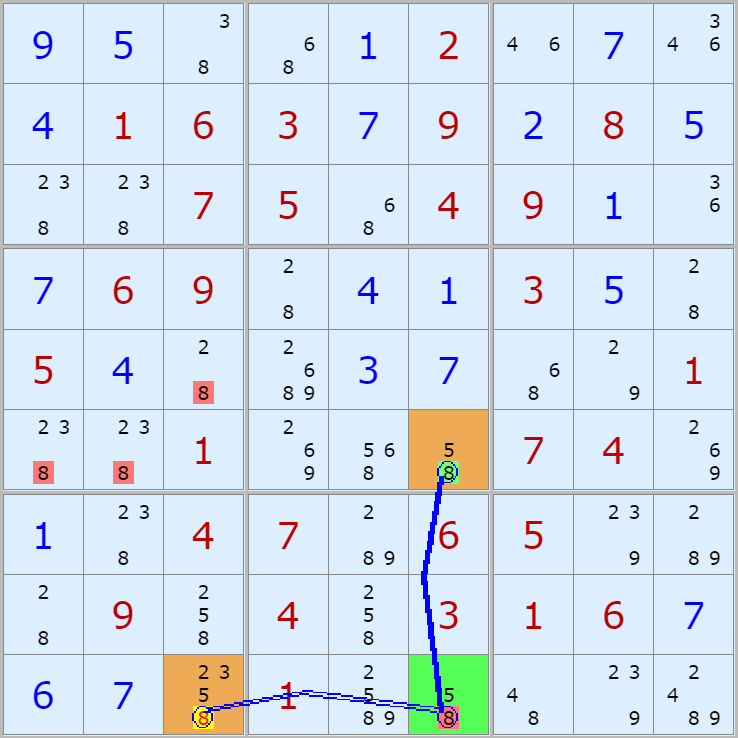
읽는 방법은

연두색 후보숫자가 시작점이 되고 노란색 후보수가 끝점이 된다.

링크를 연결한 선 중에 

실선이 스트롱 링크이고 이중실선이 위크 링크이다. 

 

 

시작점 스트롱 링크 > 끝점 위크일 경우 (예제 88개)

 

 

시작점 스트롱 링크 > 끝점 스트롱 경우 (예제 2개)

 

Andoku 스도쿠 3 - 강력 스도쿠 추천 앱

Andoku 스도쿠 3 - 강력 스도쿠 추천 앱