스도쿠-후보숫자가 많은 칸 주변을 공략해보자~

 이번 글에서는 스도쿠를 더 재미 있게 즐기기 위한 실전 팁에 대해 알아 보도록 하겠다. 가장 큰 팁부터 이야기 하자면 '후보숫자가 많은 칸 주변부터 공략하자!'이다. 나는 스린이일 때는 초반에 풀하우스를 다 찾았는지 알지 못하기 때문에 1~9를 거의 무한반복으로 누르면서 찾다가 갑자기 공식을 쓸만한 숫자가 보이면 본격적으로 풀기 시작했는데...

 

 최근에 발견한 스도쿠 공식 적용을 위한 타겟을 정할 때, '후보숫자가 많은 칸 주변의 이중값' 부터 공략하기 시작하니 좀 더 잘 보이기 시작했다. 

 

 실제로 전문가급 1게임을 진행하면서 위에 말한 '후보숫자 많은 칸 주변 이중값 공략'이 주요한 이유를 알아보도록 하겠다. (초보자에게는 어려운 공식도 있겠지만 이번 글의 목표는 '후보숫자가 많은 칸'을 공략하면 좀 더 시간 낭비를 중이는 것에 대한 글이기 때문에 이해를 하기 힘들어도 끝까지 보기를 권한다. 물론 설명도 적을테니 공부 차원에서 맛보기를 해도 좋다.)

 

 쓰인 공식은 

심플 컬러링(=싱글 체인), 심플 컬러링(=싱글 체인) 확장, 핀드 X윙, 확실한 페어, 핀드 X윙, 핀드 소드피쉬, 사시미 소드피쉬, 사시미 젤리피쉬, XY 체인, 풀하우스(2회)로

 

 초급공식 3회, 중.고급 공식 8회 모두 '후보숫자가 많이 남은 칸 주변의 이중값을 공략해서 찾는 것을 볼 수 있다.

 

이 글에서는 나타나지 않지만 XY윙에서도 유효한 것을 발견했다. 

 

 또한 1가지 더 이야기 하고 싶은 것은 심플컬러링과 X윙 정도 알게된 중수를 위한 것인데...

 

 우리가 보통 체인 기술을 쓸 때, 시작점 OFF와 끝점 ON이 되는 후보숫자 X가 마주보는 X를 제거한다고 알고 있는데, 당연히 맞는 말이지만 좀 더 높은 공식을 이해하기 위해서는 후보숫자 X가 ON일 때와 OFF일 때 2가지의 적용 후 공통되게 후보숫자 X를 지울 수 있기 때문에 제거하는 것이 아니고 시작점이 ON이던 OFF던 간에 해가 하나만 나오는 1가지의 공식으로 증명을 하는 개념을 익혀야 한다. 사실 방법은 같은데 우리가 인지하는 방식이 다르다.

 

 우리가 보통 아는 방식ON 또는 OFF일 때 교집합 2가지 공식으로 증명하는 방법과 1가지 공식으로 증명하는 방식 2가지로 기술하겠다. 1가지의 공식으로 증명을 하는 개념을 꼭 이해하기를 바란다. 

 

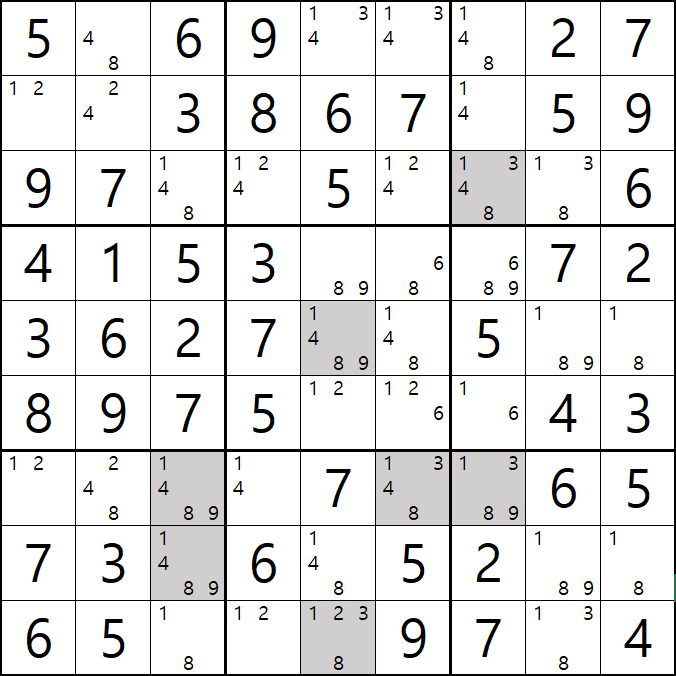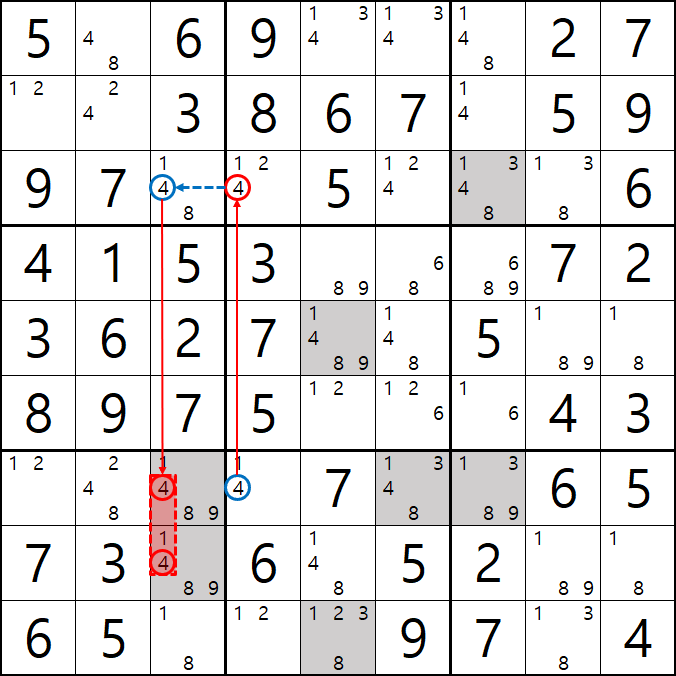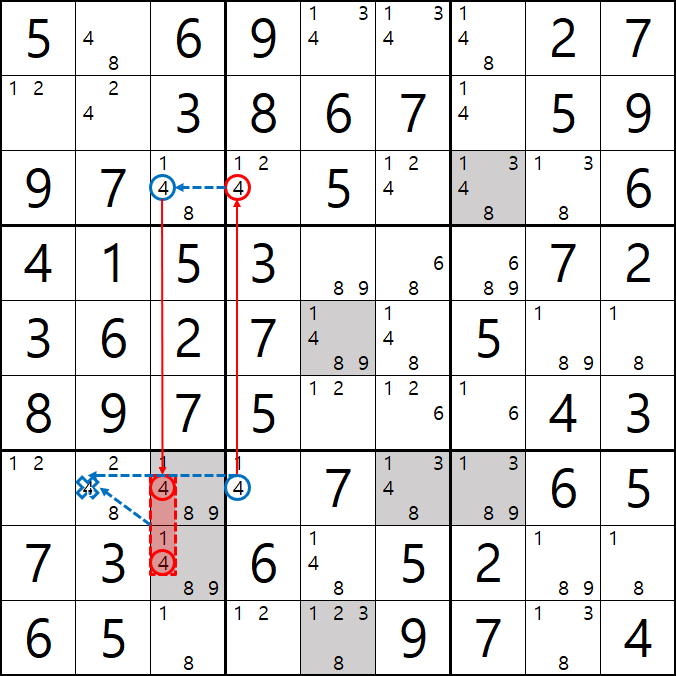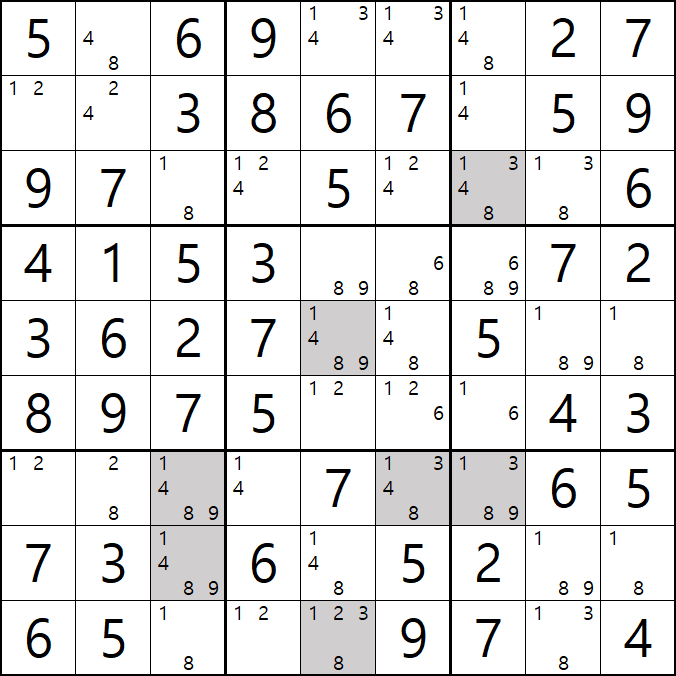
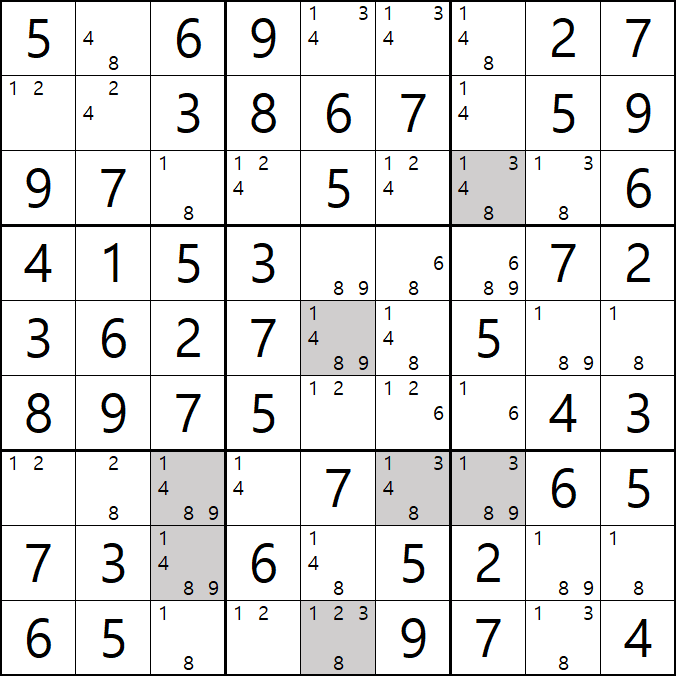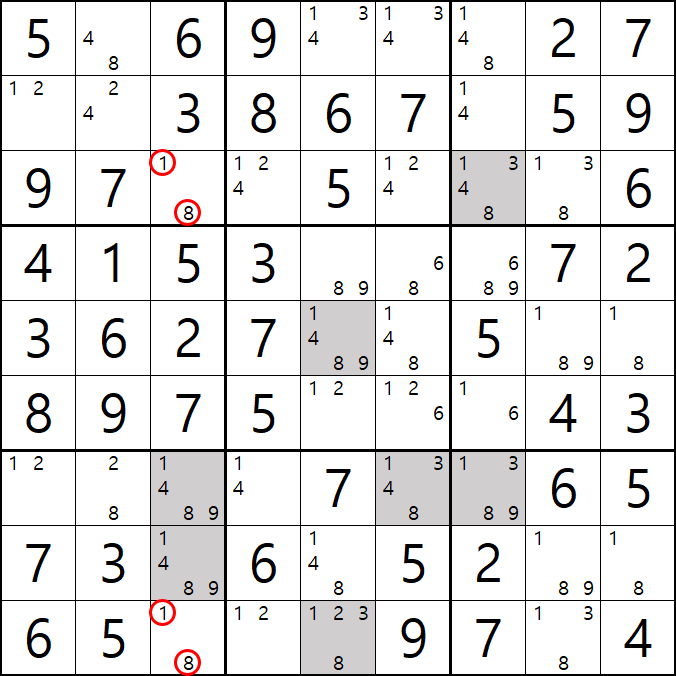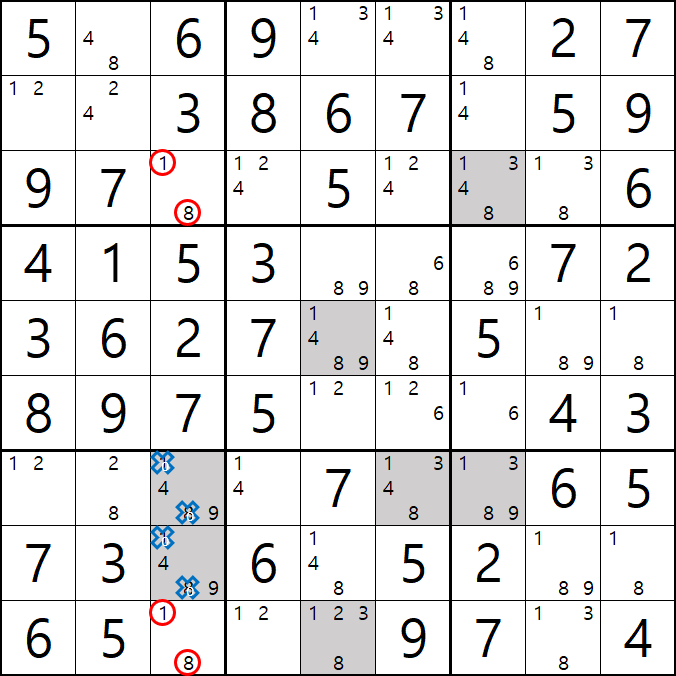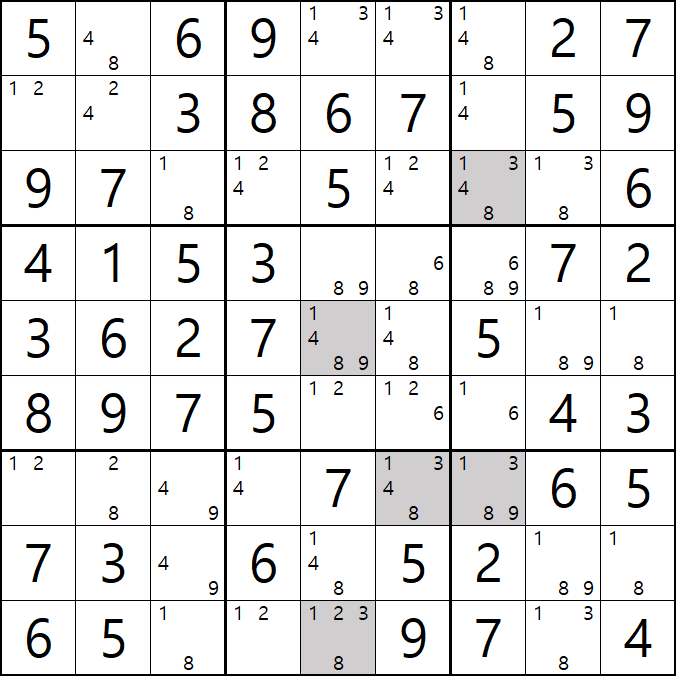
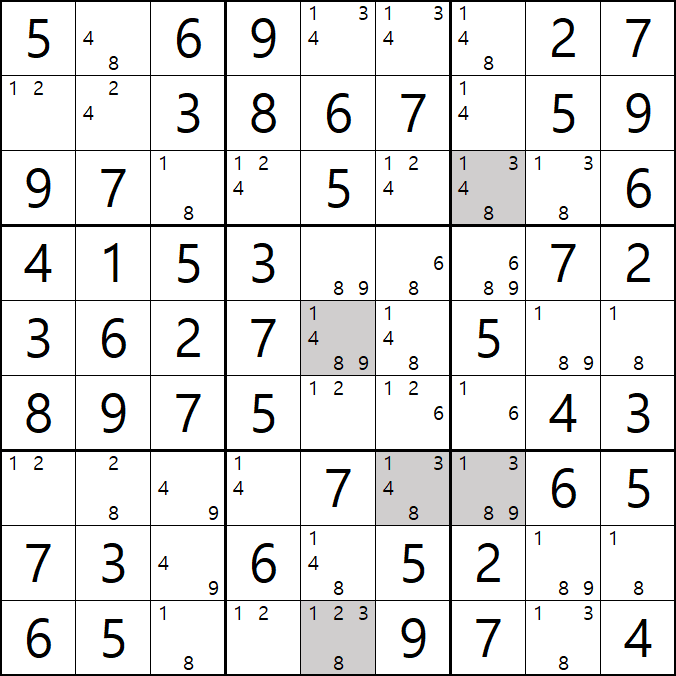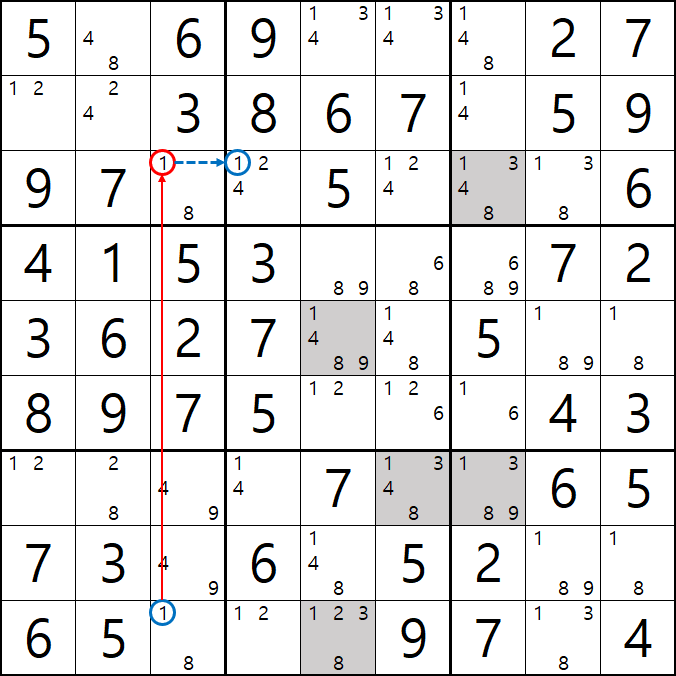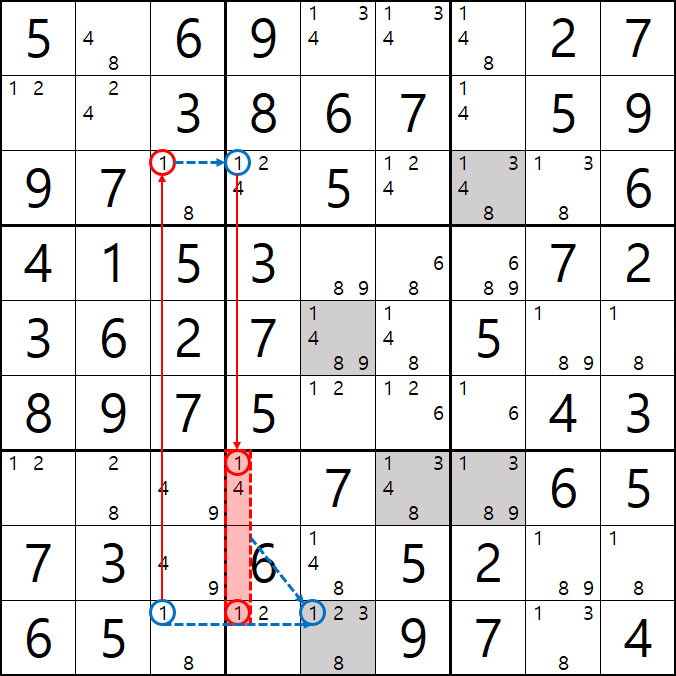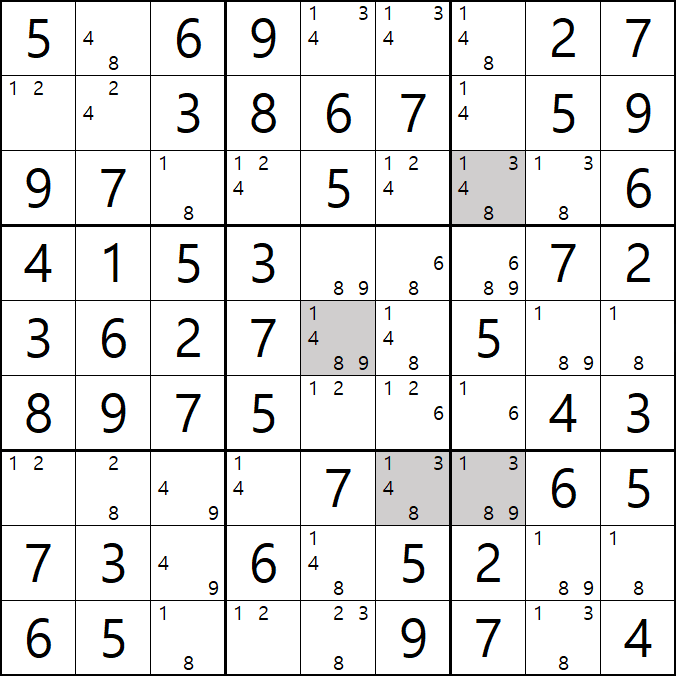
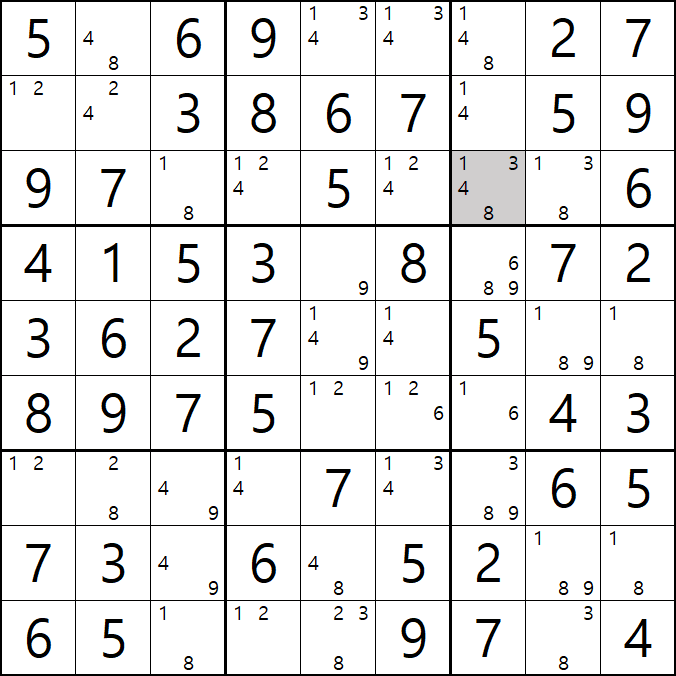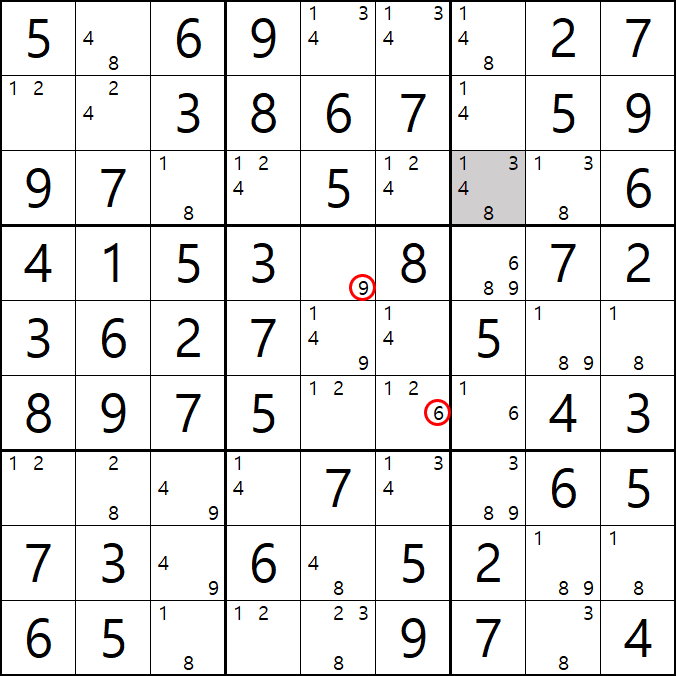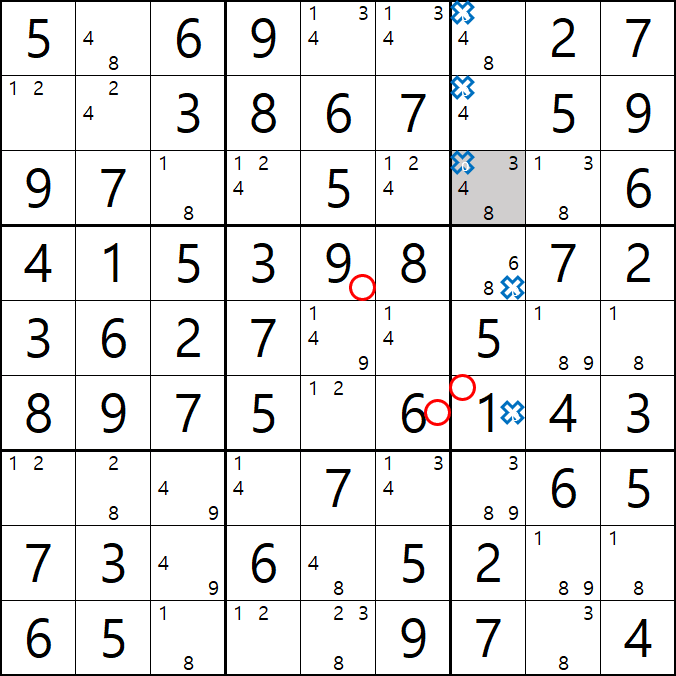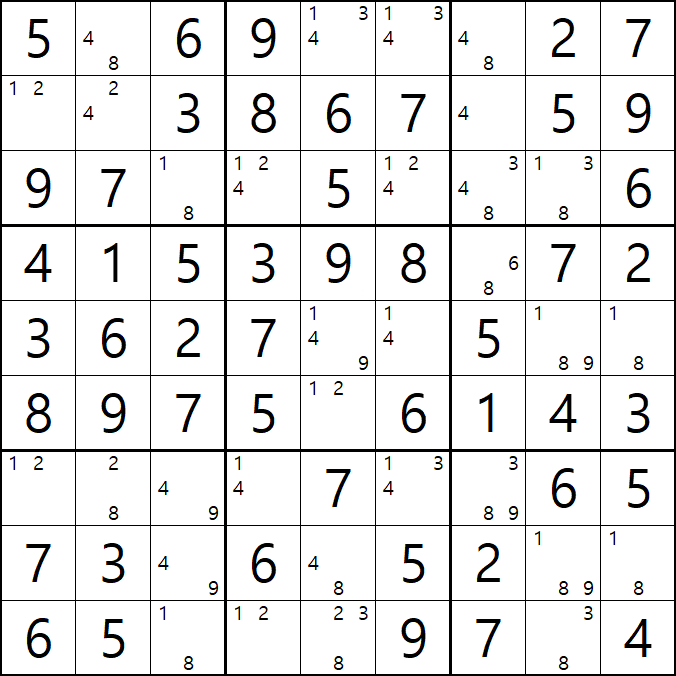
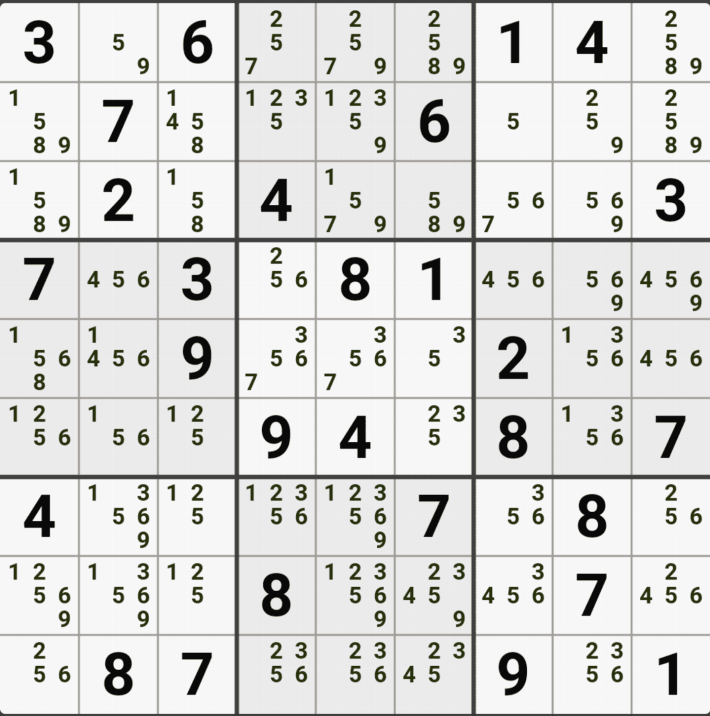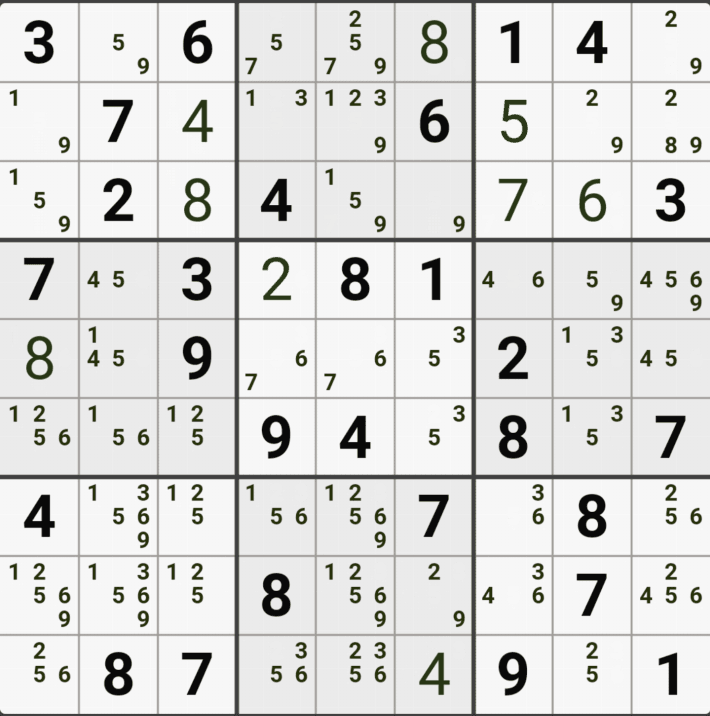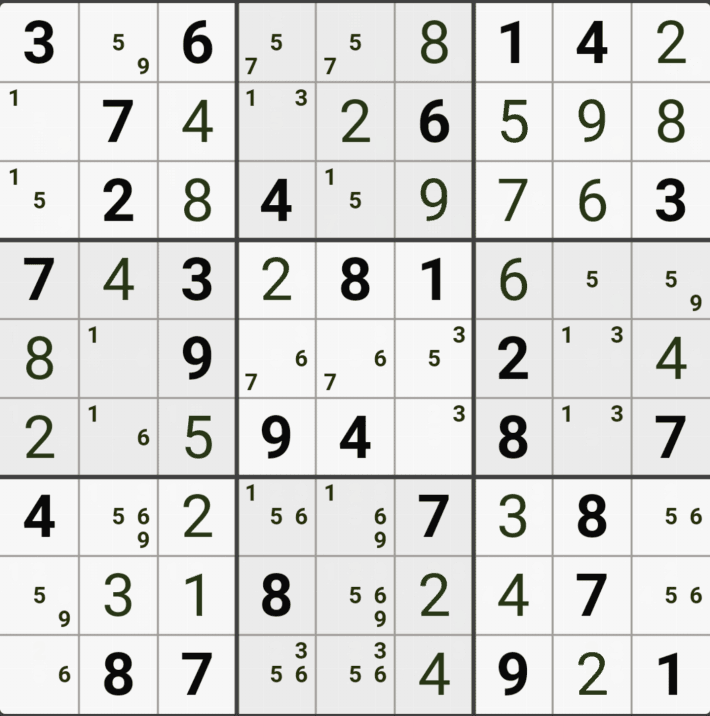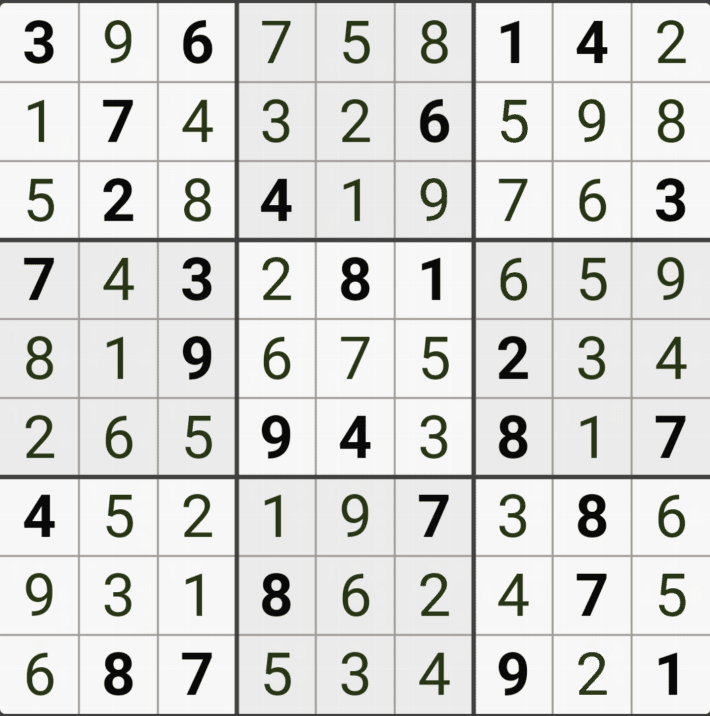
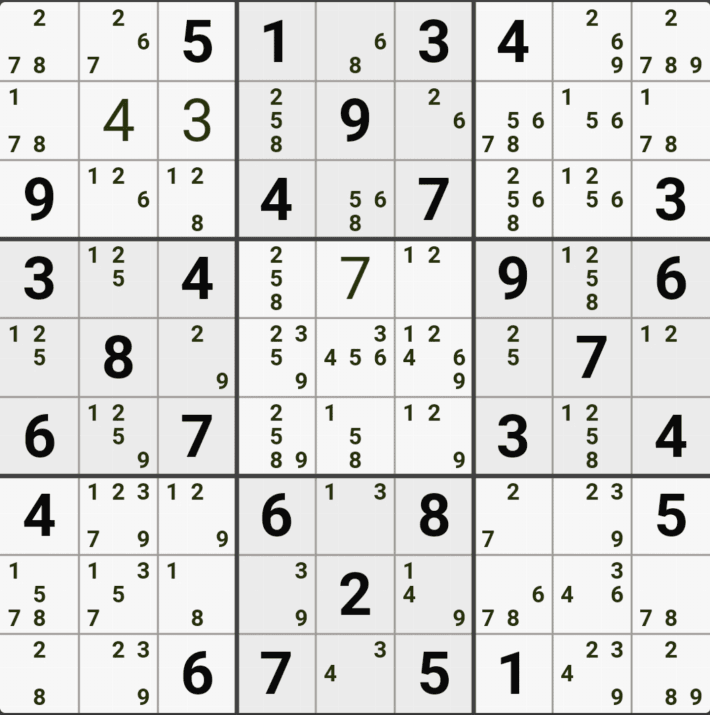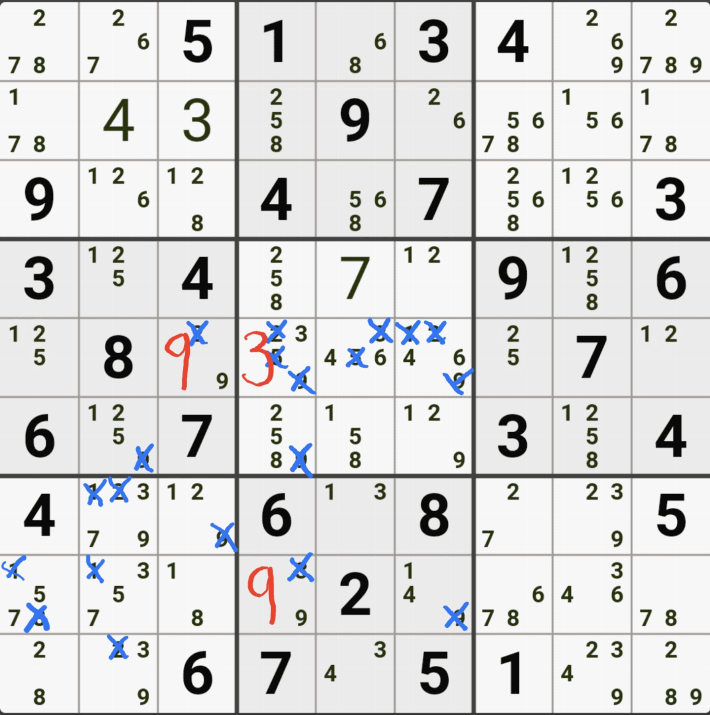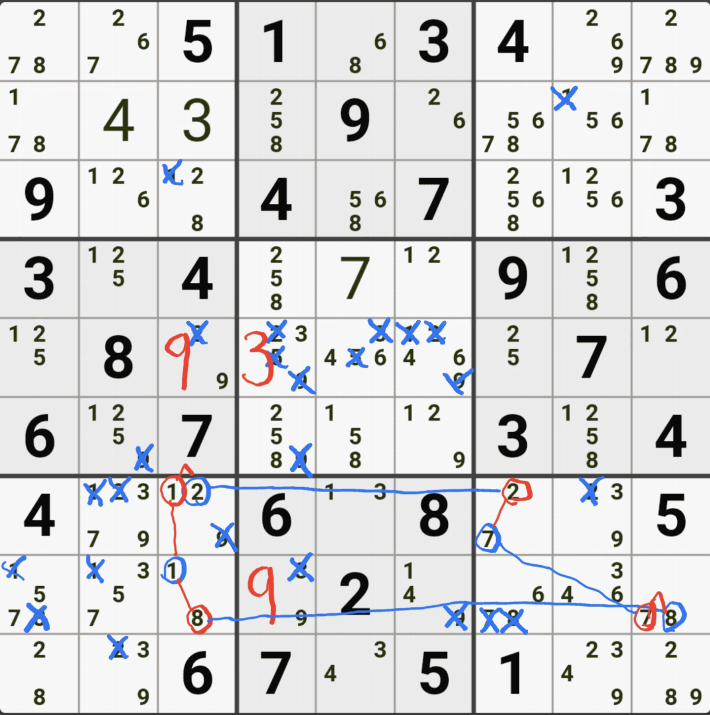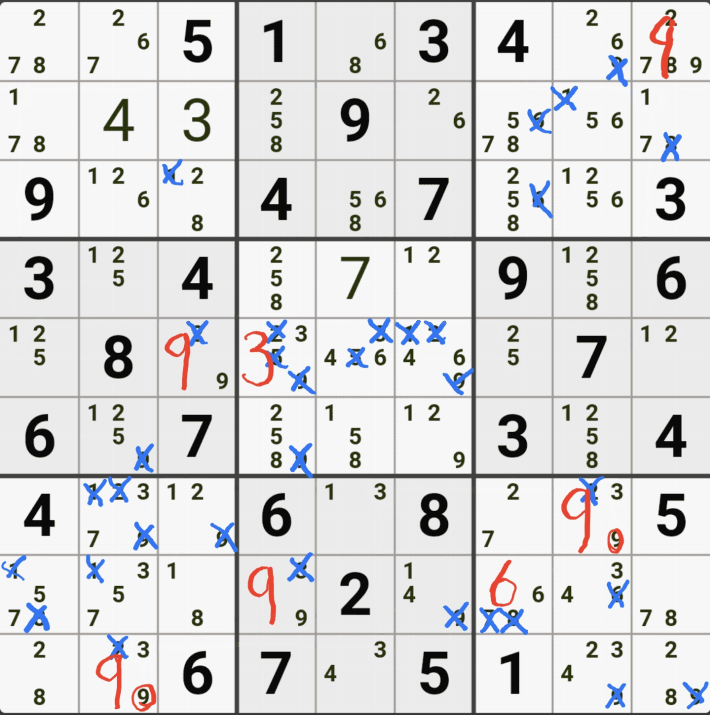
1. 아래와 같이 초반에 풀하우스 > 포인팅 페어 등으로 초반의 풀하우스를 확정한 후에 제일 많은 후보수가 남은 9칸에 회색을 칠했다. 이제 이 칸을 중심으로 어떻게 풀어 나가는지 보자!!

 

 

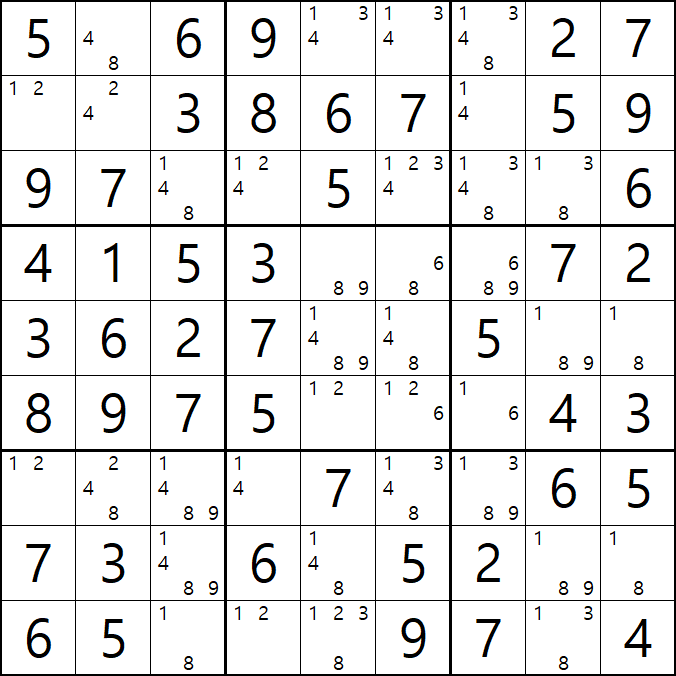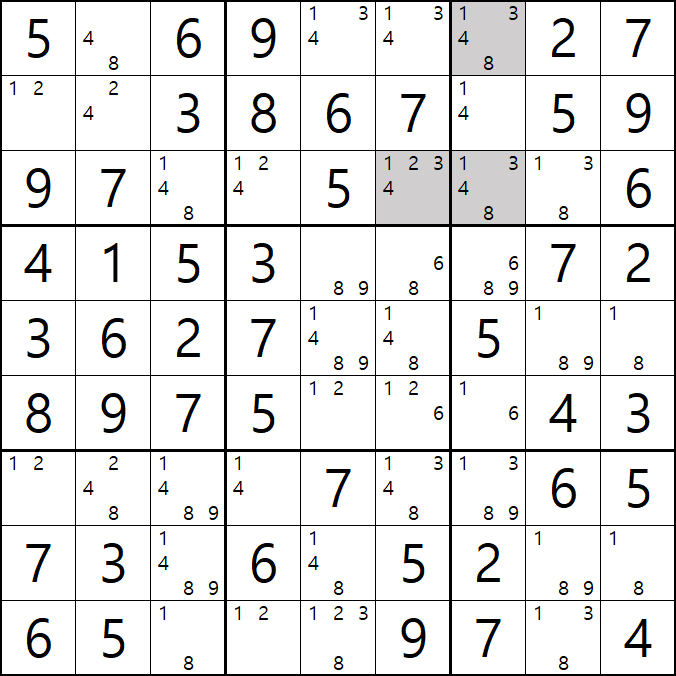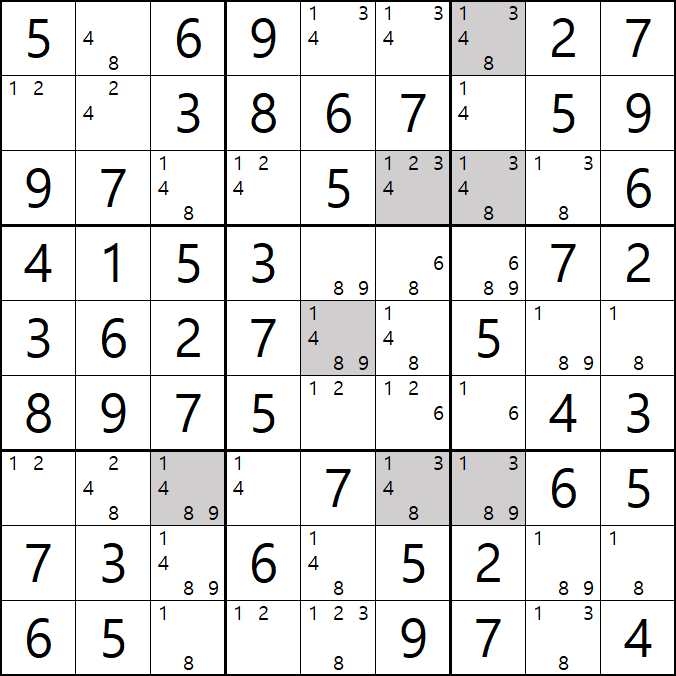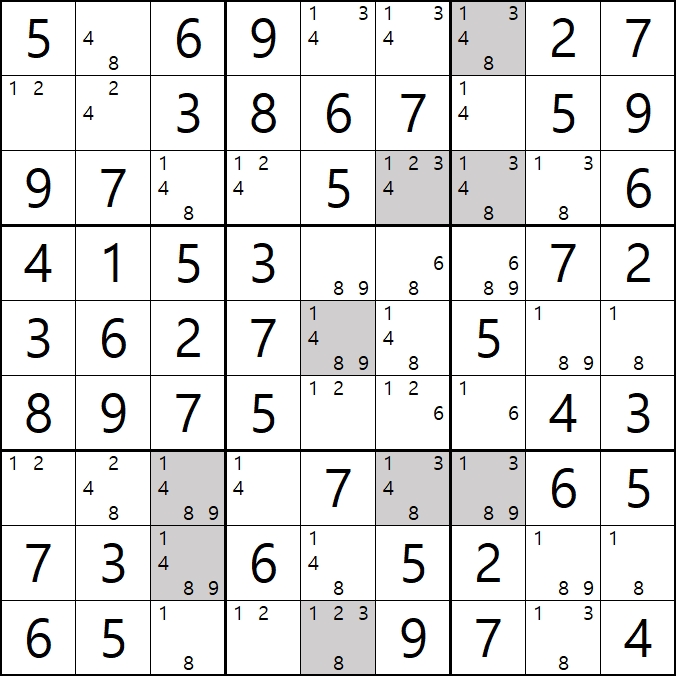
움짤 예제 1.

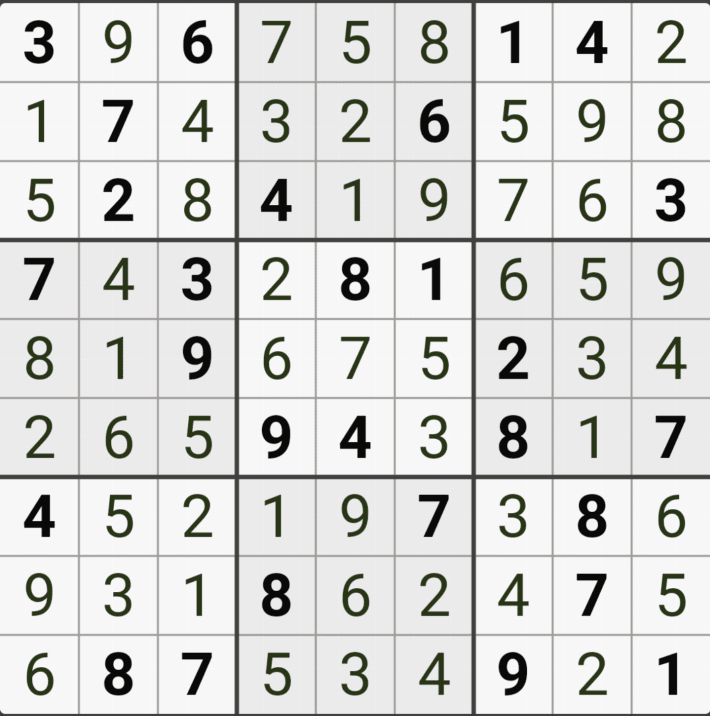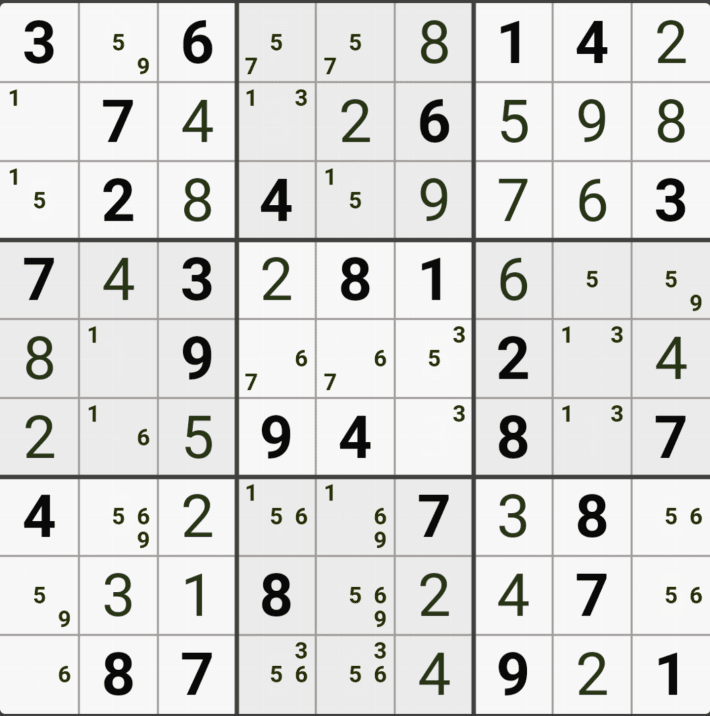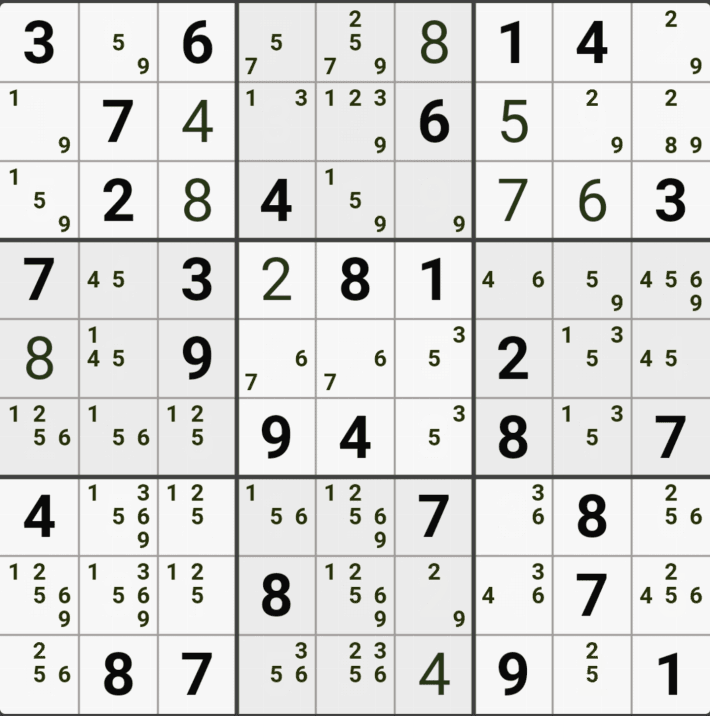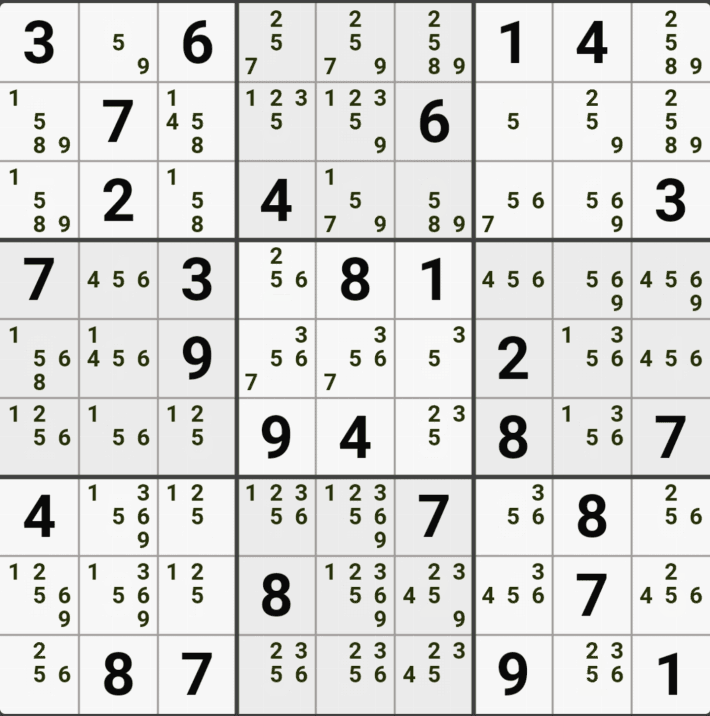
1번 공식 심플 컬러링(=싱글 체인)

1/3/4/8[A7] 회색1번 축소

 

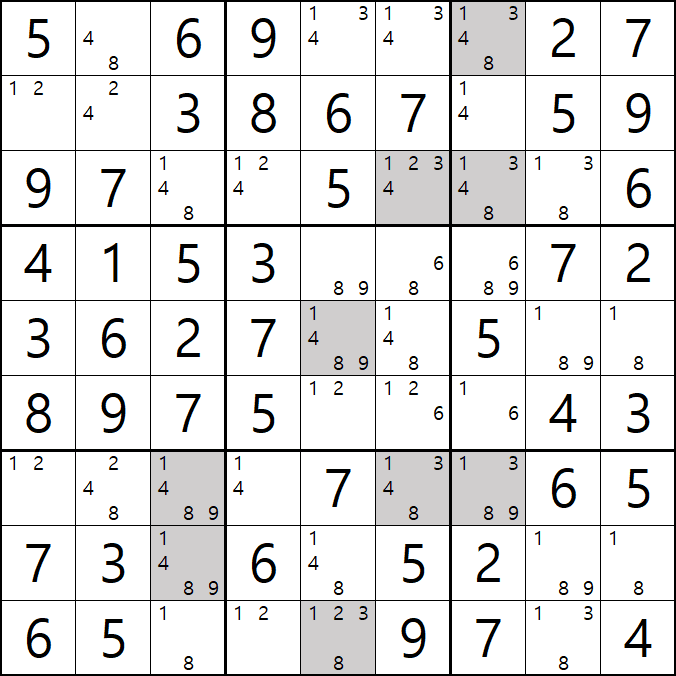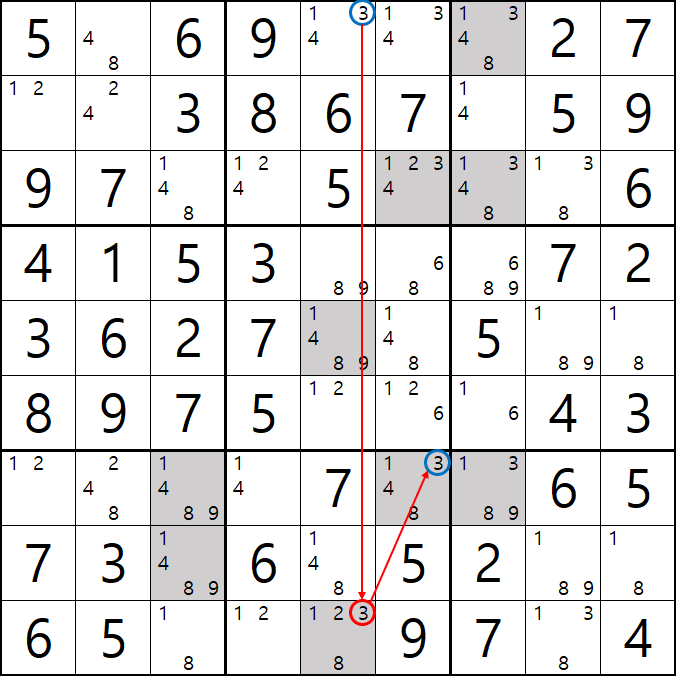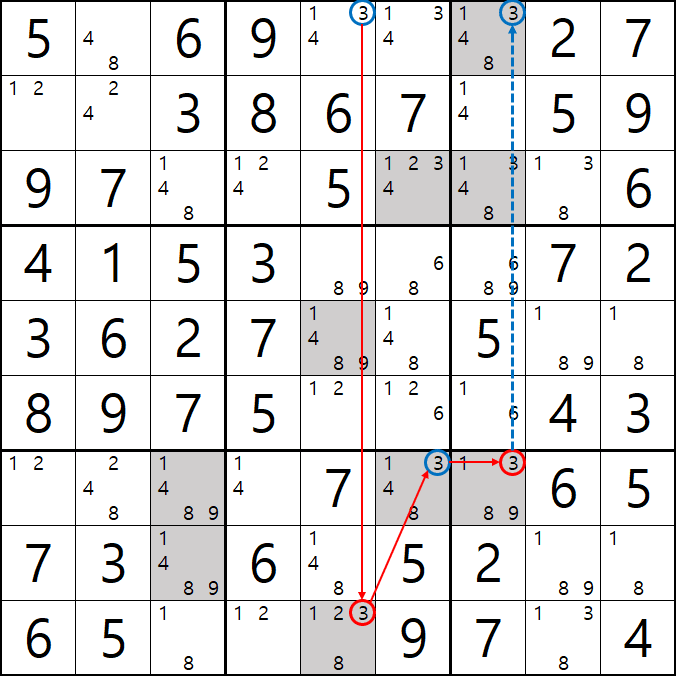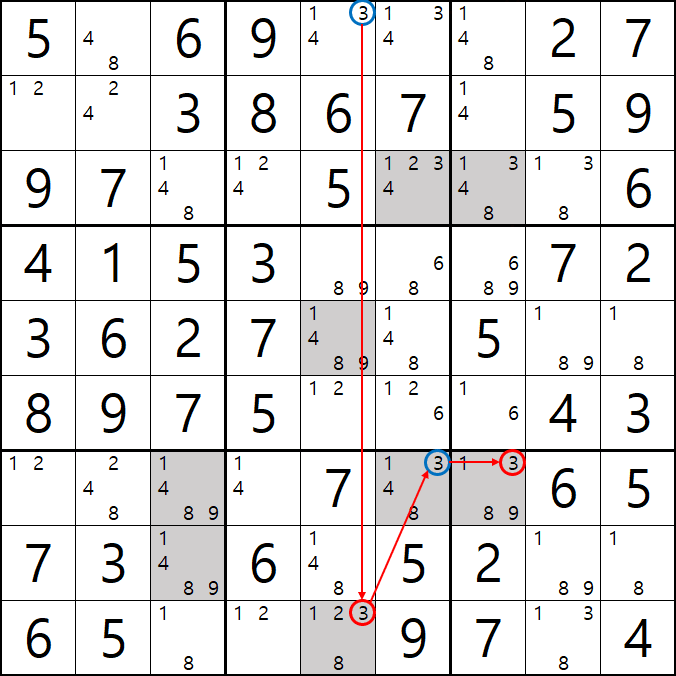
1가지 증명 방법

 

-3[A5] +3[I5] -3[G6] +3[G7] -3[G7] +3[A5] 가 되어 

-3[A5]와 +3[A5]가 중첩되는 모순이 발생하기 때문에

-3[G7]을 제거할 수 있다. 

 

(이 개념은 -3[A5]을 +3[A5]으로 시작해도

+3[A5] -3[I5] +3[G6] -3[G7] +3[G7] -3[A5] 이 되어

+3[A5]와 -3[A5]이 중첩되는 모순이 발생하기 때문에

+3[G7]을 제거할 수 있다.

라는 같은 결과를 얻을 수 있음을 알 수 있다.) 

 

2가지 증명 방법

 

-3[A5] +3[I5] -3[G6] +3[G7]일 때

-3[A5]과 +3[G7]이 마주보는 3[G7]을 제거할 수 있다. 

 

움짤 예제 2 .

2번 공식 심플 컬러링(=싱글 체인, 사실 포인팅 페어로 적용가능)

1/2/3/4[C6] 회색2번 축소

 

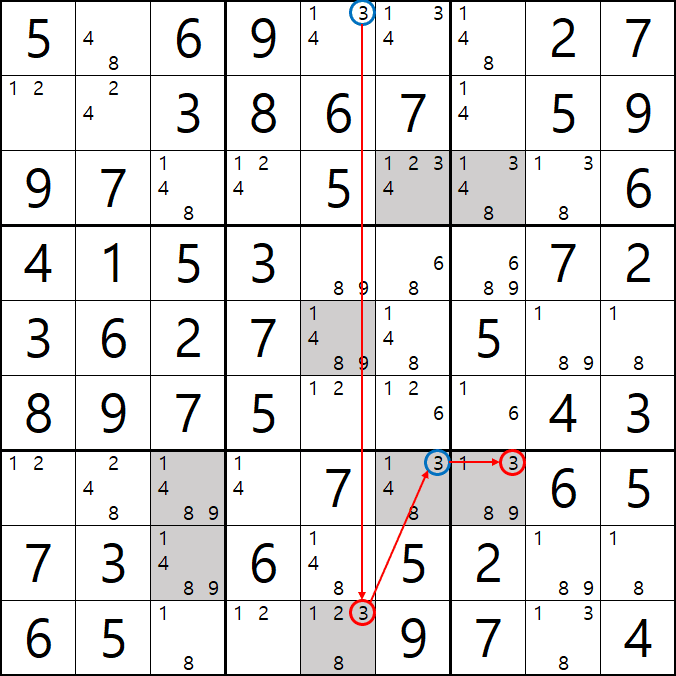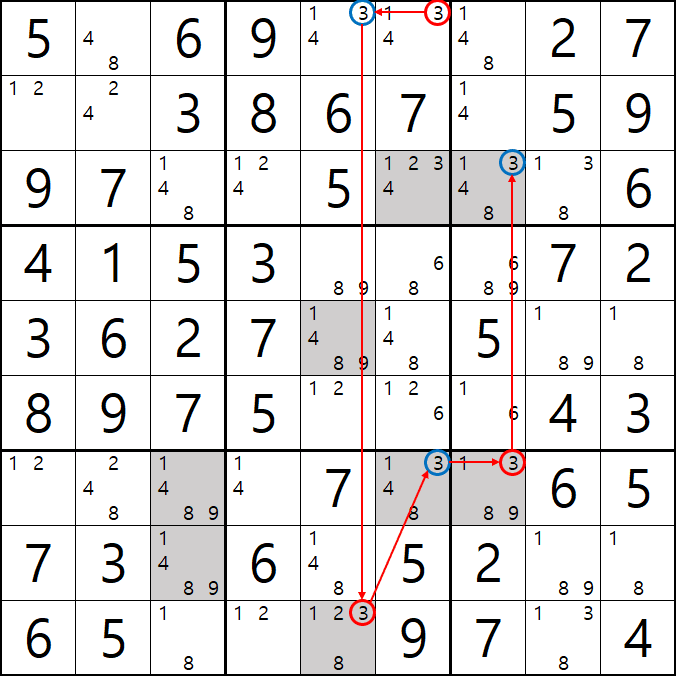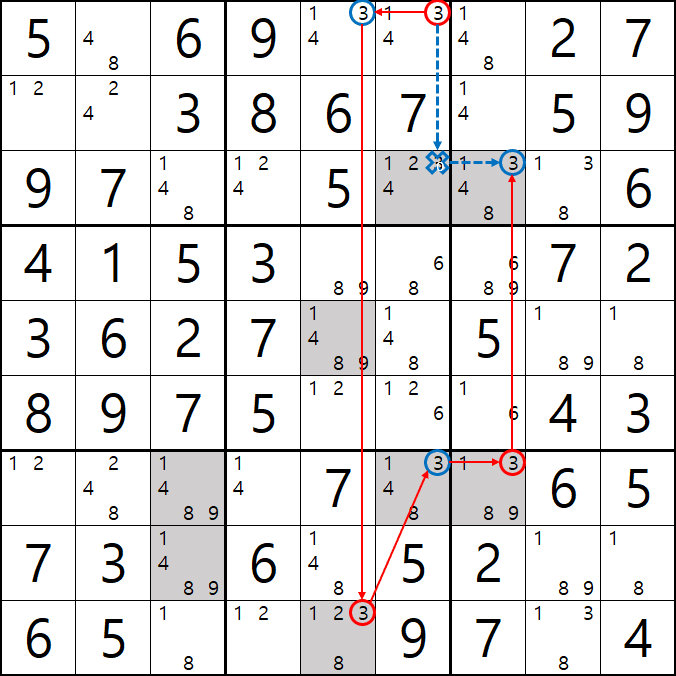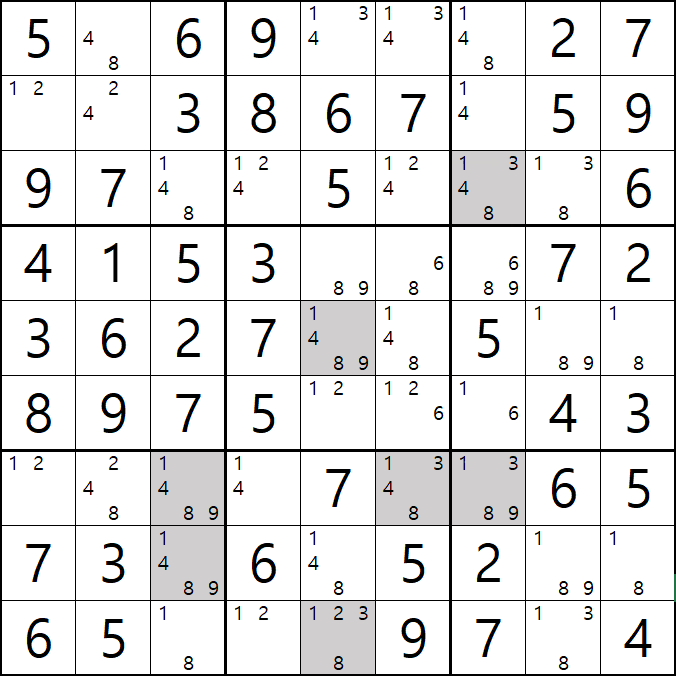
팁2 > 위의 움짤을 보면 알겠지만 스트롱 링크로만 이어지는 심플컬러링은 해를 1개 찾은 이후 스트롱 링크로 확장될 수 있다.(여기에 더 해서 모든 체인은 스트롱 링크로만 연결된다면 확장이 가능하다. 3D 메두사라는 공식이 대표적이다.)

 

 사실 3[B7], 3[B8] 포인팅 페어로 제거 가능하지만 스트롱 링크로만 이뤄진 심플컬러링은 확장될 수 있다는 것을 알려 주고 싶었다. 

 

1가지 증명 방법

 

+3[A6] -3[A5] +3[I5] -3[G6] +3[G7] -3[C7] +3[C6] -3[A6] 이 되어 

+3[A6]와 -3[A6]가 중첩되는 모순이 발생하기 때문에

+3[C6]을 제거할 수 있다. 

 

2가지 증명 방법

-3[C7] +3[G7] -3[G6] +3[I5] -3[A5] +3[A6] 이 되어

-3[C7] +3[A6]이 마주보는 3[C6]을 제거할 수 있다. 

 

움짤 예제 3 .

3번 공식 핀드 X윙 

후보숫자 3칸 축소

 

팁3. 핀드 X윙을 모양만 익힌 스도커가 있을 텐데, 그룹 X체인으로 이해 하는 것이 찾기도 좋고 적용하기도 좋다. 이 개념은 사시미 X윙에도 동일하게 적용된다. 또한 스트롱 링크 또는 위크 링크에 상관없이 이런 방식으로 찾은 후에 핀드-사시미 소드피쉬인지 젤리피쉬인지 판단하는 것도 좋은 방법이라고 본다. 

 

1가지 증명방법

 

 -4[G4] +4[C4] -4[C3] +4[G3&H3] -4[G2]가 되어 

G열에 -4[G4]과 -4[G2] 1개의 하우스에 OFF가 동시에 존재하는 모순이 발생하기 때문에

모순을 제거하기 위해서 -4[G2]는 제거할 수 있다. 

 

2가지 증명방법

-4[G4] +4[C4] -4[C3] +4[G3&H3]가 되어

-4[G4]과 +4[G3&H3]이 동시에 마주보는 -4[G2]를 제거할 수 있다. 

 

움짤 예제 4.

4번 공식 확실한 페어

1/4/8/9[G3&H3] 회색3,4번 축소

 

 

1/8[C3] 및 1/8[I3]이 확실한 페어가 되어 

1/8[G3] 및 1/8[H3] 제거 가능

 

움짤 예제 5.

5번 공식 핀드 X윙

1/4/3/8[I5] 회색5번 축소

 

1가지 증명방법

 

 -1[I3] +1[C3] -1[C4] +1[G4&I4] -1[I5]가 되어 

I열에 -1[I3]과 -1[I5] 1개의 하우스에 OFF가 동시에 존재하는 모순이 발생하기 때문에

모순을 제거하기 위해서 -1[I5]는 제거할 수 있다. 

 

2가지 증명방법

 -1[I3] +1[C3] -1[C4] +1[G4&I4] 가 되어

 -1[I3] +1[G4&I4] 이 동시에 마주보는 1[I5]를 제거할 수 있다. 

 

움짤 예제 6.

6번 공식 핀드 소드피쉬

후보숫자 3칸 축소

 

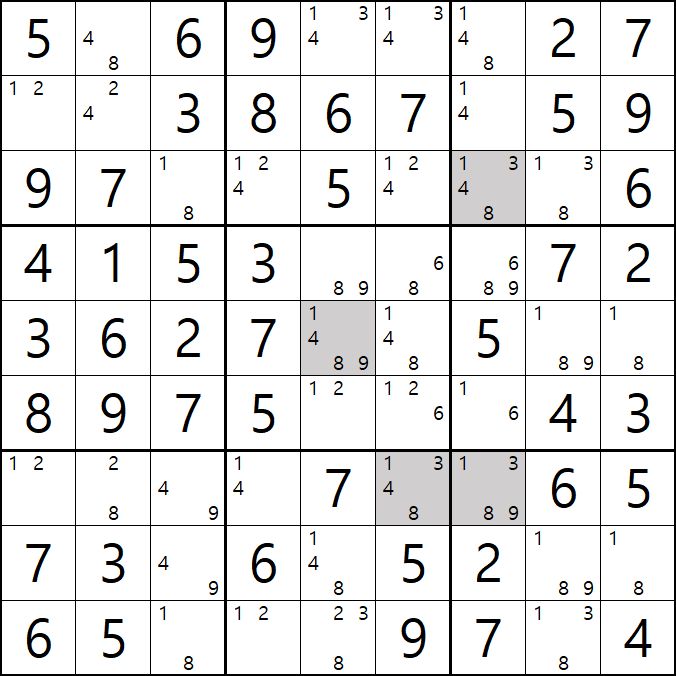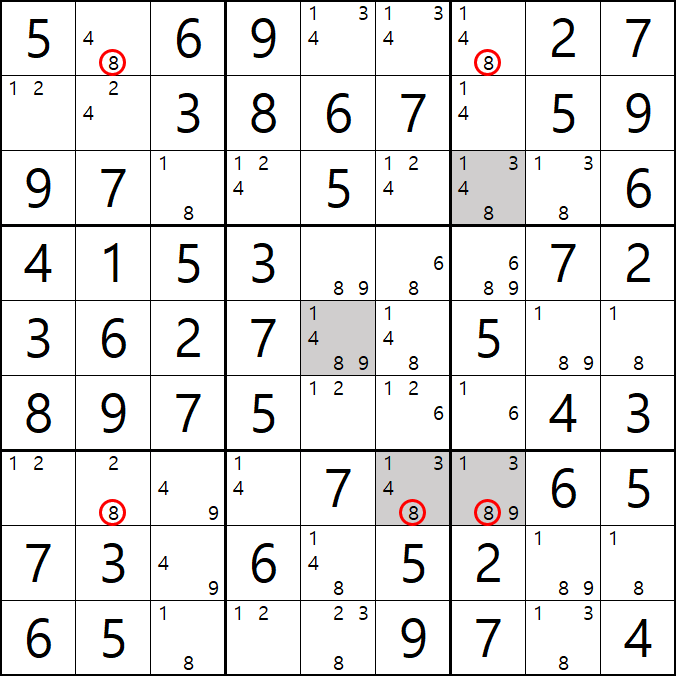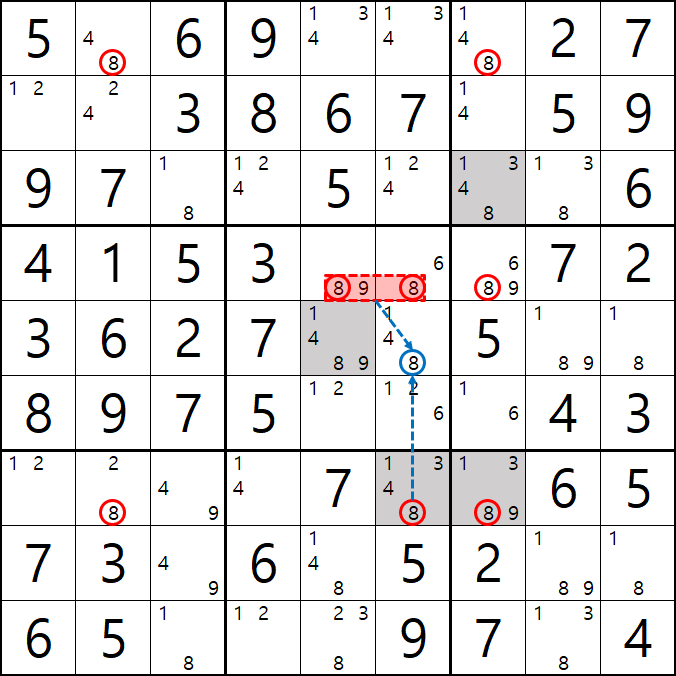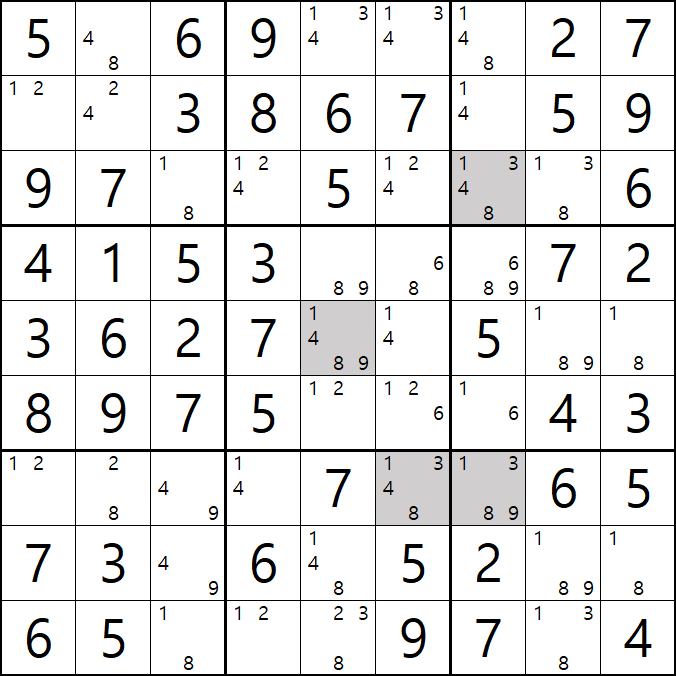
8[A2], 8[A7]

8[D5&D6], 8[D7]

8[G2], 8[G6], 8[G7]

 

이 핀드 소드피쉬가 되어 

8[D5&D6]와 8[G7]이 마주보는 8[E6]를 제거할 수 있다. 

 

(소드피쉬와 젤리피쉬는 체인으로 설명하기가 아직 어렵다.)

 

움짤 예제 7.

7번 공식 사시미 소드피쉬

1/3/8/9[G7] 회색6번 축소

 

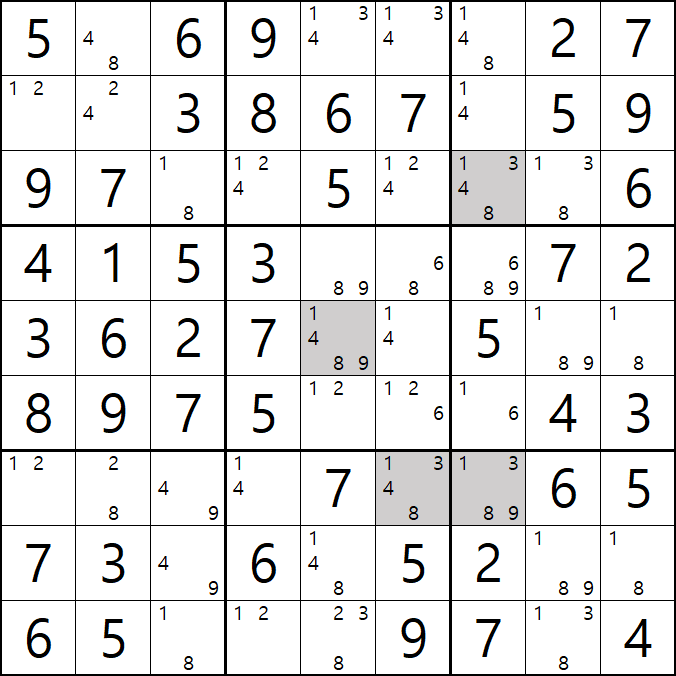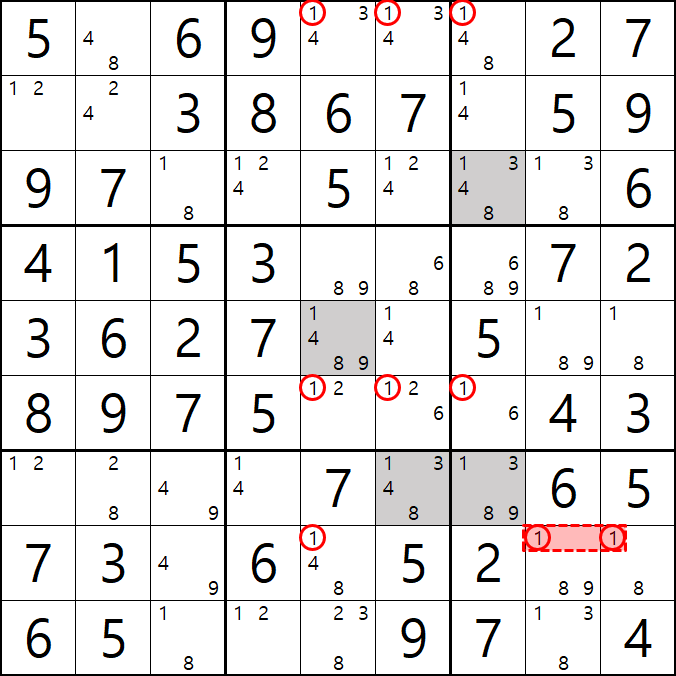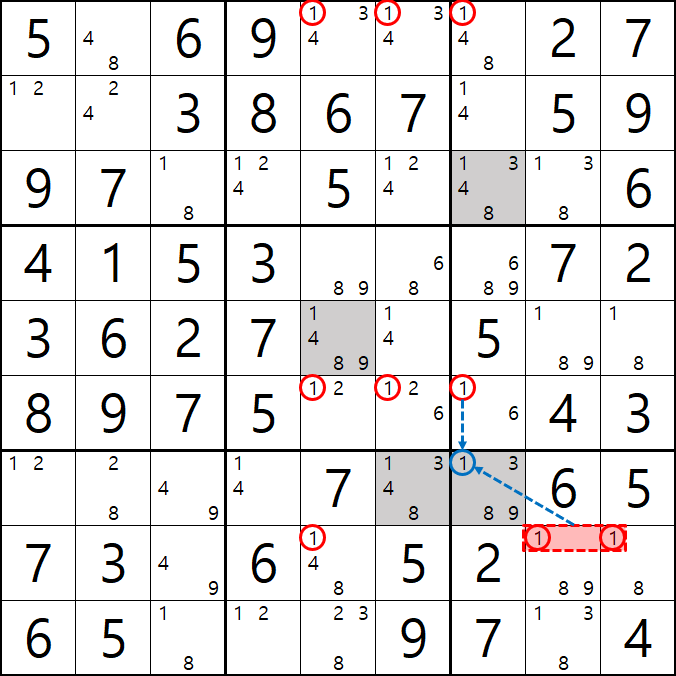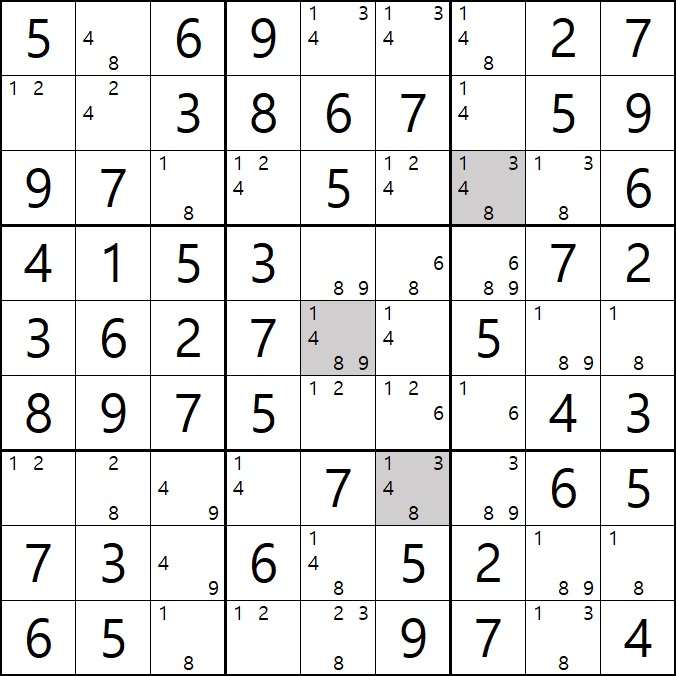
1[A5], 1[A6], 1[A7]

1[F5], 1[F6], 1[F7]

1[H5], 1[H8&H9]

가 사시미 소드피쉬가 되어 

 

1[F7] 과 1[H8&H9]이 마주보는 1[G7]을 제거할 수 있다.

 

움짤 예제 8.

8번 공식 사시미 젤리피쉬

 

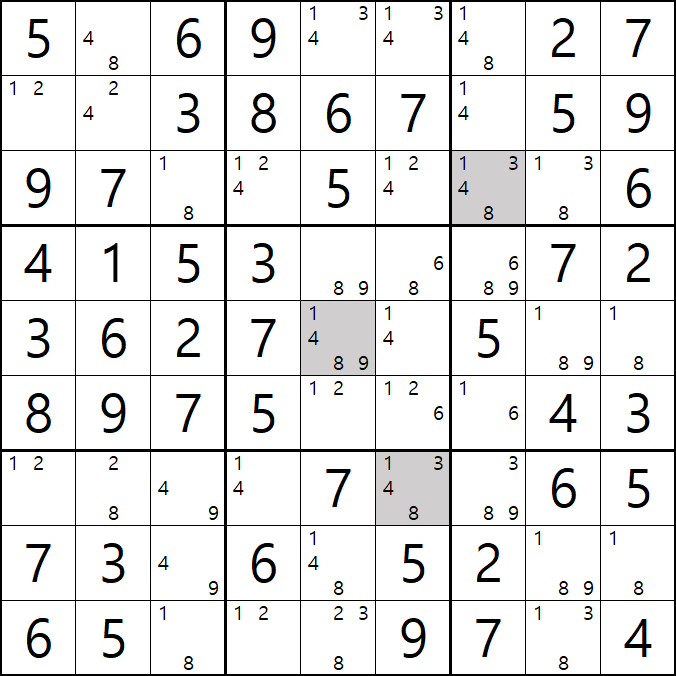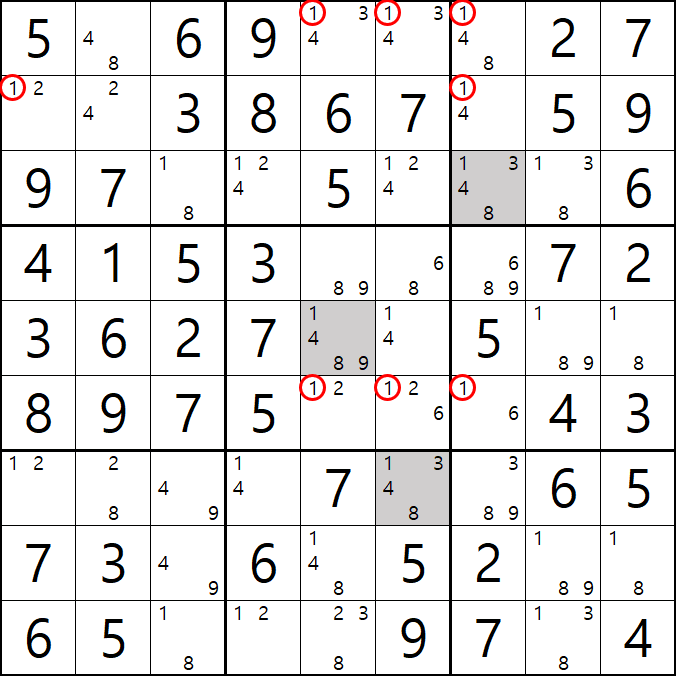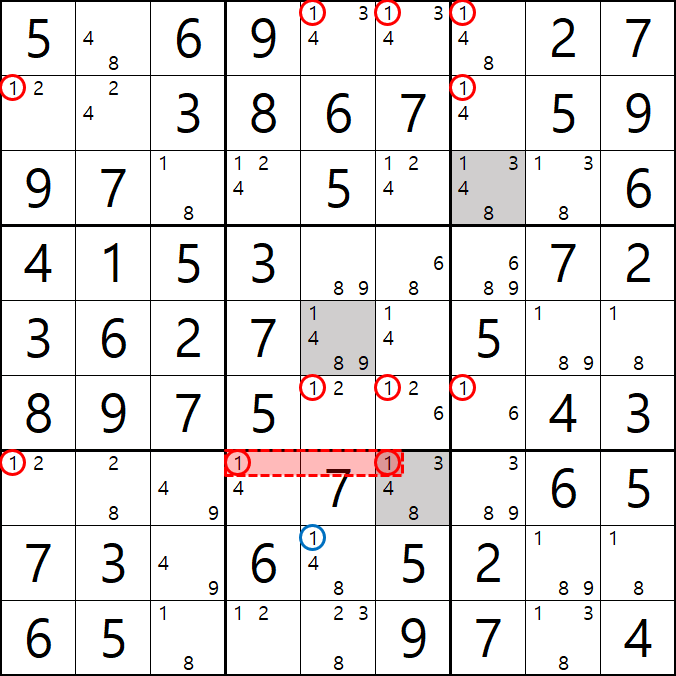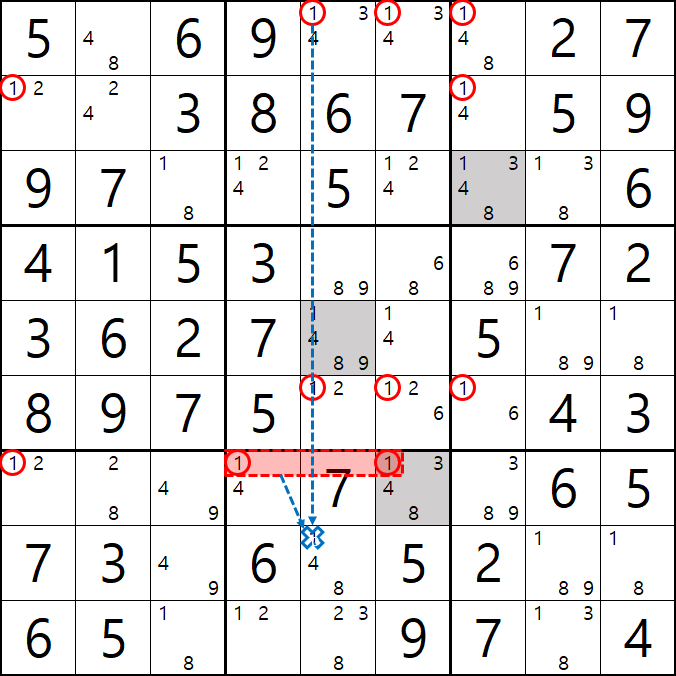
1[A5], 1[A6], 1[A7]

1[B1], 1[B7]

1[F5] , 1[F6], 1[F7]

1[F1], 1[F4&F6]

이 사시미 젤리피쉬가 되어 

 

1[F5]와 1[F4&F6]이 마주보는 1[F5]를 제거할 수 있다. 

 

움짤 예제 9.

9번 공식 XY 체인

1/3/4/8[G6] 회색7번 축소

 

1가지 증명

-8[G2] +2[G2] -2[G1] +2[G1] -1[G4] +4[G4] -4[H5] +8[H5] -8[G6] +8[G2]이 되어 

-8[G2]과 +8[G2]이 중첩되는 모순이 발생된다. 

따라서 이런 모순을 없애기 위해서 -8[G6]를 제거하여야 한다. 

 

2가지 증명

-8[G2] +2[G2] -2[G1] +2[G1] -1[G4] +4[G4] -4[H5] +8[H5] 가 되어

-8[G2] 과 +8[H5]가 마주보는 8[G6]을 제거할 수 있다. 

 

움짤 예제 10.

10번 풀하우스

1/4/8/9[E5] 회색8번 축소

 

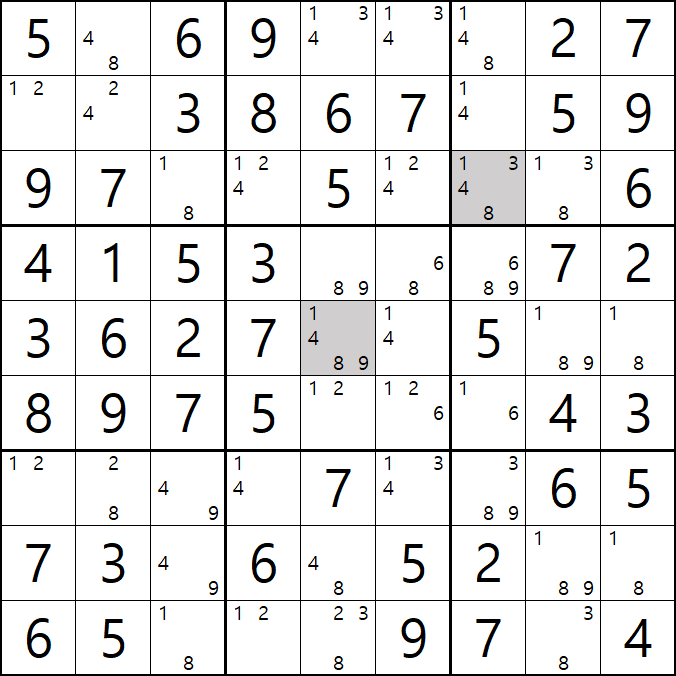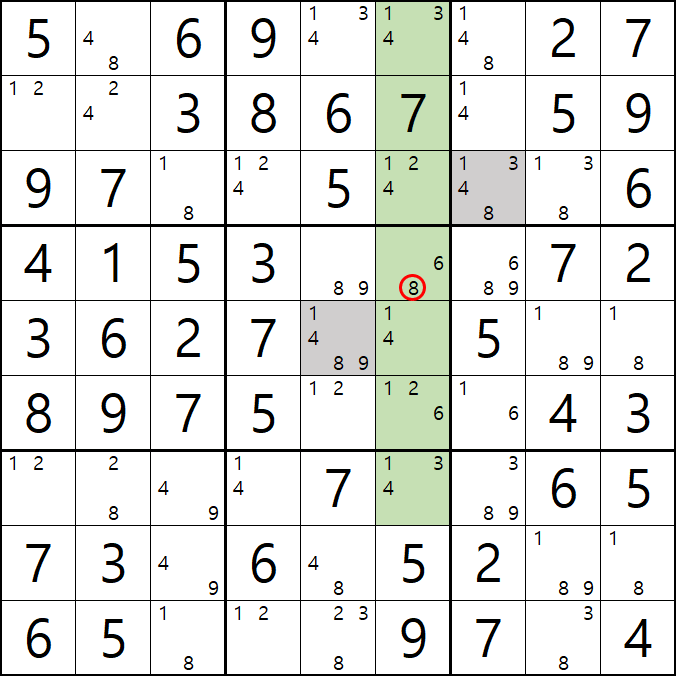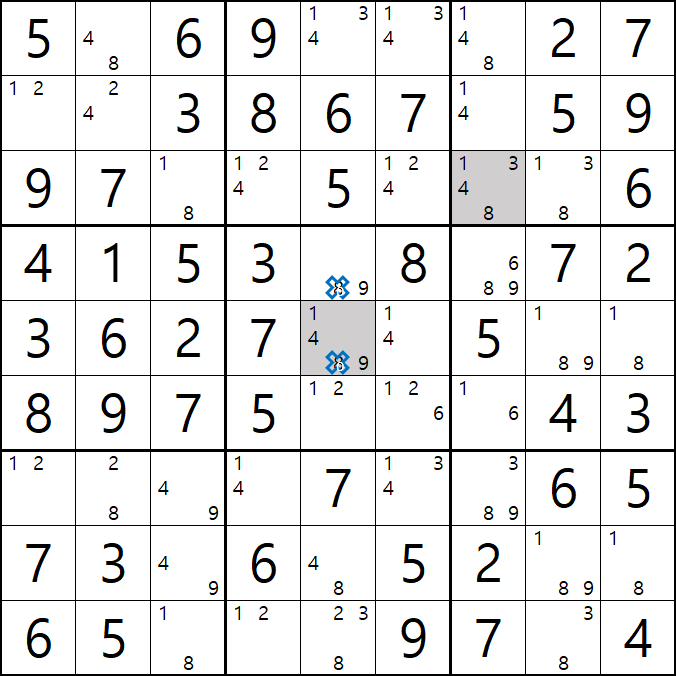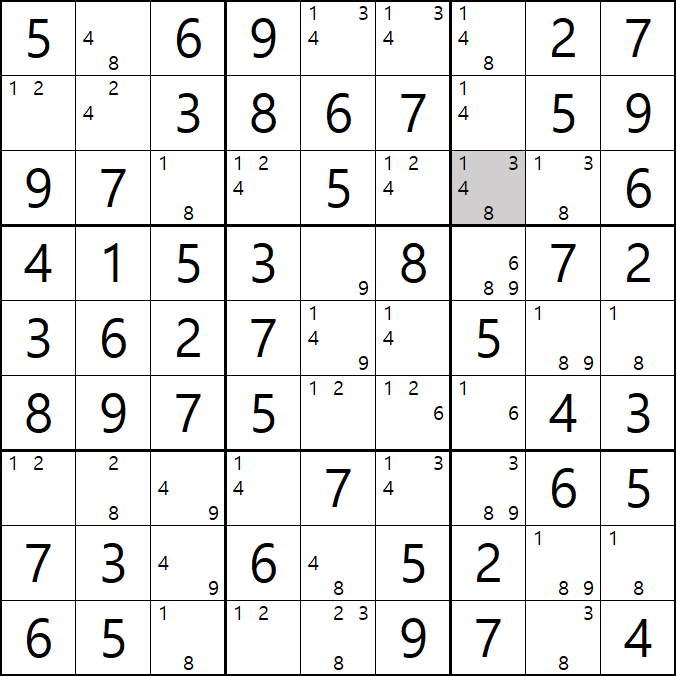
8[D6]이 6열에 대한 풀하우스가 되어 

8[D5], 8[E5]을 제거할 수 있다. 

 

움짤 예제 11.

11번 풀하우스

1/3/4/8[E5] 회색9번 축소

 

 

1[F7]이 F열에 대한 풀하우스가 되어 

1[A7], 1[B7], 1[C7]을 제거할 수 있다. 

 

움짤 예제 12. 풀하우스~로 끝까지

이렇게 4개의 후보숫자로 이뤄진 회색칸 9칸을 지우고 난 후에 아래 움짤과 같이 풀하우스로 끝까지 풀리는 것을 알 수 있다. 

 

즉, 후보숫자가 많은 칸부터 공략하는 것이 맞다는 증명은 되지는 않겠지만(스도쿠는 50억가지의 경우의 수가 있다고 한다.) 한 가지의 사례는 되겠다. 

 

이번 글에서 말하고 싶은 팁을 정리하면 아래와 같다. 

 

1. 현재 많이 남은 후보숫자가 있는 칸의 후보숫자를 중점적으로 보며 공략하자!

 

 어쩌면 너무 당연한 법칙이라 팁이라고도 할 수 없을지도 모른다. 마지막 81번째 칸에 후보숫자 1개만 남는 것을 역으로 보면 계속 후보 숫자 칸은 계속 늘어나기에 당연할 수도 있지만..

 

그럼에도 불구하고 무조건 공식적용을 위한 서칭을 하기보다는 매우 유용하다고 보는 전략이다. 

 

 

 위에서 살펴본 본 움짤예제 1~10까지는 후보숫자가 많은 4개짜리 9칸과 3개짜리 2칸에서 후보숫자가 제거되는 것을 알 수 있다. 다만 게임 초반에 후보숫자 5~8개 남은 칸은 피하자. 이건 다른 숫자를 찾으면서 제거해야하는 폭탄이다.

 

2. 체인공식을 쓸 때는 이제 모순이 되는 상황을 제거한다는 개념을 익히자! 풀하우스부터 체인까지 모든 공식은 이런 모순이 되는 후보숫자를 제거한다고 봐도 무방하다. 

 

3. 스트롱 링크로만 연결된 체인은 확장을 하여도 항상 참이 된다. 

 

4. 핀드 X윙, 사시미 X윙을 접근할 때는

핀 또는 사시미라고 불리는 2~3칸을

그룹 링크로 엮어서 그룹 링크 X윙으로 찾는 연습을 하자

 

5. (이건 지극히 개인적인 소견이지만) 소드피쉬 시리즈와 젤리피쉬 시리즈는 체인공식만으로 설명하기 어렵다. (나처럼 뭔가 있을까 해서 그룹 체인까지 엮어서 찾다가 지치지 않기를 바란다.)

 

추가 

 

6. 너무도 당연한 이야기 이지만 공식을 써서 지워지는 숫자에 주목하면 계속 전체 숫자를 스캔하지 않고도 다음 공식을 위한 후보숫자가 잘 보일 수 있다. 아래는 좀 지저분 하지만 1개의 시발점을 찾으면 어떻게 숫자끼리 상호 작용을 하는지 숫자를 계속 따라가는 움짤이다. 풀하우스가 나오면 바로 지우기만 하기보다는 확정숫자가 나올 때 어떤 숫자가 없어지는지 좀 더 여유롭게 보면서 게임을 즐기기를 권한다.

 

 물론 모든 숫자가 지워지는 것을 보자는 것은 아니다. 히든 싱글 및 포인팅 페어, 포인팅 트리플로 어지간한 확정숫자를 찾고 난 이후에 우리가 공식 또는 체인이라는 전략으로 찾은 후부터 지워지는 숫자에 주목하면 될 것이라고 본다. 

 

 

스도쿠를 더 즐기기 위한 유용한 실전 팁 I

스도쿠를 더 즐기기 위한 유용한 실전 팁 I