움짤로 익히는 스도쿠 5. 트리플 제거, 숨겨진 트리플, 확실한 트리플

 이번 글에서는 스도쿠의 기본공식으로 불리지만 실제로는 매우 어려운 숨겨진 트리플(Hidden Triple), 쉽지만 강력한 트리플 제거(Pointing Triple), 패턴만 눈에 익으면 잘 보이는 확실한 트리플(Naked Triple)에 대해 알아 보도록 하겠다. 

 

복습차원에서 페어 시리즈 움짤을 먼저 한번 보고 가겠다.

 

 아래는 페어 제거 움짤이다. . 

 

페어 제거는 위의 움짤 처럼 박스안에 후보숫자 X가 2개만 존재할 때도 성립이 되고,

아래와 같이 행. 또는 열에 걸쳐서 후보숫자 X 2개만 존재하면 

박스안에 있는 잠긴 후보숫자 X가 있는 칸 외의 후보숫자 X도 지울 수 있다고 했다. 

 

 

다만 페어 제거를 위해서는 후보숫자 X, 2개는 박스안에 동시에 존재해야 한다. 

 

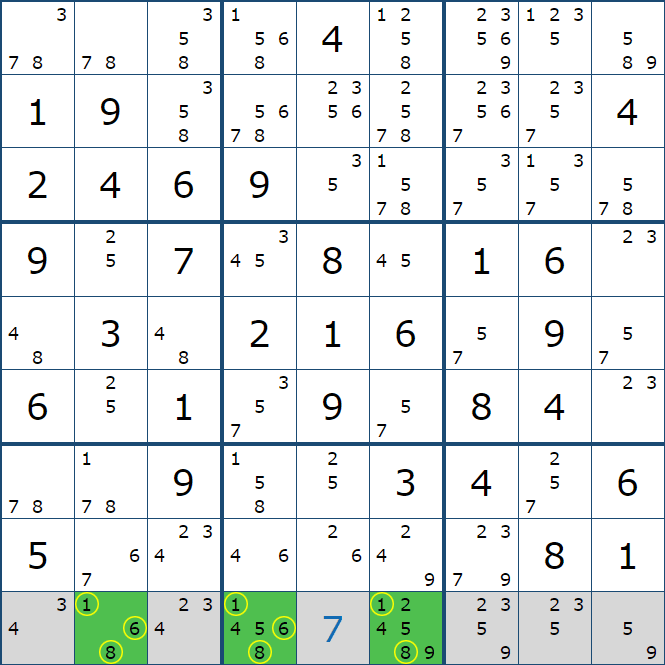
트리플 제거는 당연히 여러분이 예상하는대로 위의 움짤이 아래와 같이 후보숫자의 갯수만 3개로 늘어 난다~

 

1. 트리플 제거(Pointing Triple)

 

 하우스(박스 / 행 또는 열)에 동일한 후보숫자 X가 연속된 3개의 칸에만 존재할 때,

 위치를 특정할 수는 없지만 3개의 칸 중 한 칸에는 꼭 X가 확정숫자로 들어가야 한다는 조건에 따라

 다른 박스 및 행 또는 열에 있는 후보숫자 X를 제거 할 수 있다.  

 

 위의 움짤은 박스1에 후보숫자 5, 세칸이 2행에 나란히 존재하고 있어서 '잠긴 상태'라고 표현 하며 연속으로 연결된 방향에 있는 행의 후보숫자 5, 네 칸을 지울 수 있다. 

 

 

 또한 3칸이 연속된 후보숫자 5가 행 또는 열에 존재하지 않는다면 속해있는 박스의 후보숫자 5를 지울 수 있다. 

 트리플 제거 예제 22개를 아래 더 보기를 누르면 볼 수 있다. 자료 출처는 '스도쿠 솔브'다. 

 

 

11월 8일 추가 > 움짤 예제

 

 

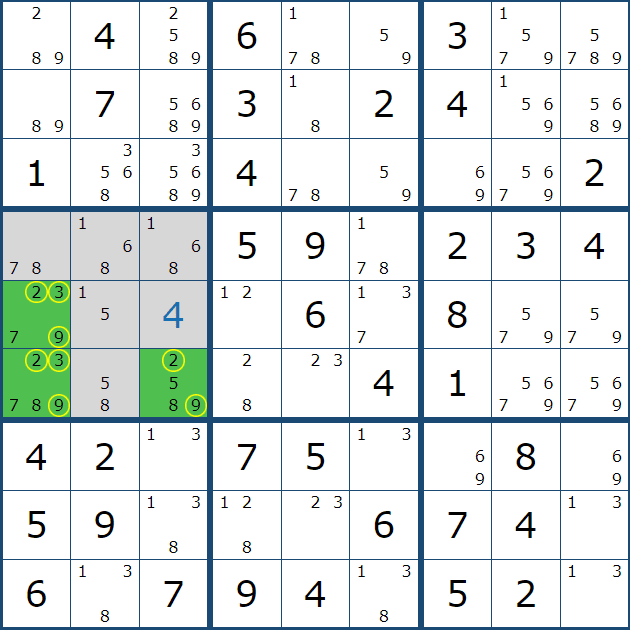
2. 확실한 트리플(Naked Triple)

 

 위의 페어 제거 개념에 다른 숫자가 똑같은 상황으로 동일하게 중첩 되면 어떻게 될까? 아래 움짤 처럼 된다. 

 

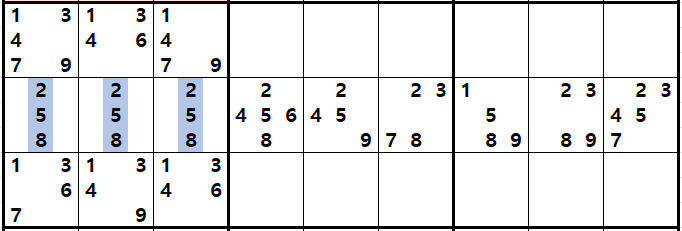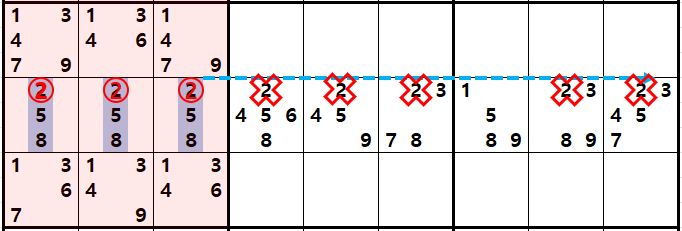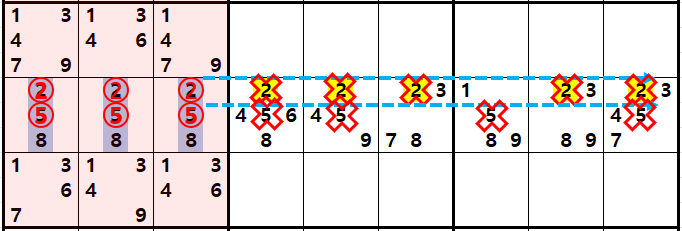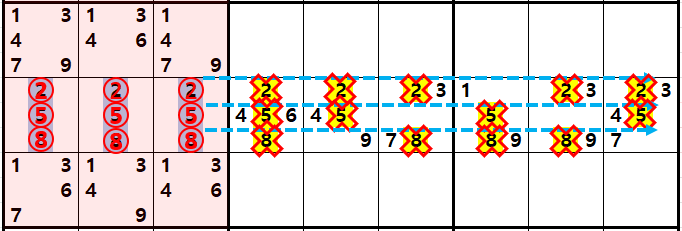
 샌드위치로 숫자가 중첩되면 각각의 숫자에 대해서 트리플 제거를 시전해 주면 된다. 즉, 동시에 후보숫자 X, Y, Z를 제거 하는 공식이 확실한 트리플이라고 불리우는 공식이다. 

 

 박스 또는 행과 열에 의해 잠긴 후보숫자 X, Y, Z가 세칸에 연속해서 들어 있는 경우에

 이를 확실한 트리플이라고 하며 연속된 방향의 행과 열 또는 속해 있는 박스의 후보숫자 XYZ를 지울 수 있다. 

 

 다만 아무리 트리플 제거의 확장판이라고 해도 이렇게 샌드위치처럼 겹치면 생기는 특징이 하나가 있는데

 그건 바로 박스 내에서 위치가 일렬이 아닌 산재되어 있거나, 행과 열에서 박스를 벗어나도 효력을 같다는 것이다. 

 

 

 그래서 가끔은 위의 움짤과 같이 박스와 행 또는 열에 동시에 확실한 트리플이 나타나기도 한다. 

 

 이렇게 XYZ / XYZ / XYZ 형태로 나오는 트리플은 한번에 많은 후보수를 지울 수 있는 장점이 있는데 

 한 가지 어려운 점이 있다. 그것은 바로 아래와 같이 경우의 수 때문에 확실한 트리플의 모양이 변형된다는 것이다.

 

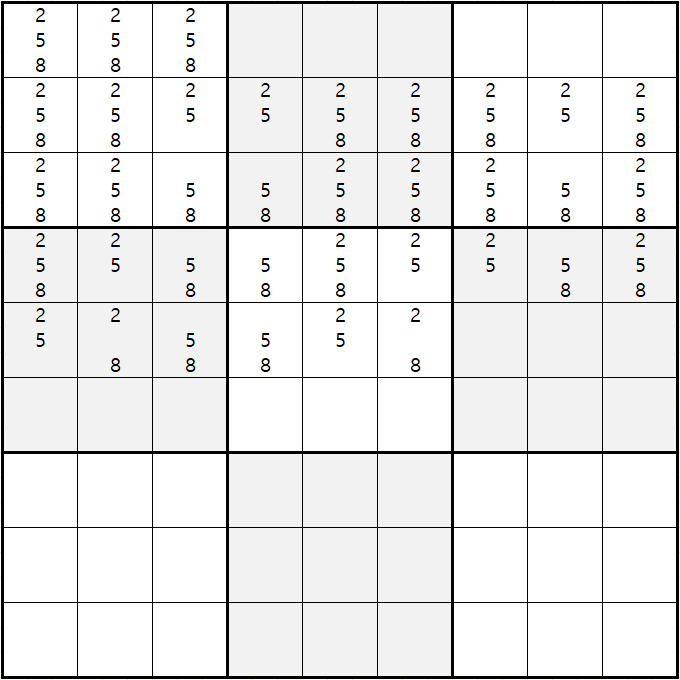
 각 행으로 연결되는 배열이 XYZ / XYZ / XYZ의 모든 숫자가 있는 형태에서 변형 되는 것인데

 열바꿈으로 인한 차이로 헷갈리는데 유형은 크게 333, 332, 322, 222 유형 네 개의 형태로 나타난다. 세분화 하면 8가지 인데 아래의 배열을 보고 332, 322, 222유형을 유심히 보자.

 

 확실한 트리플 후보숫자 유형

 

333 유형 (3칸-모든 숫자 조합 > 최대 숫자 사용 조합)

 1. XYZ / XYZ / XYZ

 

332 유형 (2칸-모든 숫자, 1칸-2개 숫자 조합)

 2. XYZ / XYZ / XY

 3. XYZ / XYZ / YZ  

 4. XYZ / XYZ / ZX

 

322 유형 (1칸-모든 숫자, 2칸-2개 숫자 조합)

 5. XYZ / XY / YZ

 6. XYZ / XY / ZX

 7.XYZ / YZ / ZX

 

222 유형 (모든 칸 2개 숫자 조합 > 최소 숫자 사용 조합)

 8. XY / XZ / YZ

 

 이렇게 네가지 유형 여덟가지 배열이 대표적인 트리플로 나타나는 형태이다. 

 

인게임에서는 258 트리플, 149 트리플 또는 14, 19 페어를 이루는 숫자들이 혼재 되기도 하고, 트리플인 줄 알았는데 트리플이 이뤄지지 않는 경우도 있어서 좀 어지럽긴 한데, 트레이닝으로 익숙해져야 한다. 

 

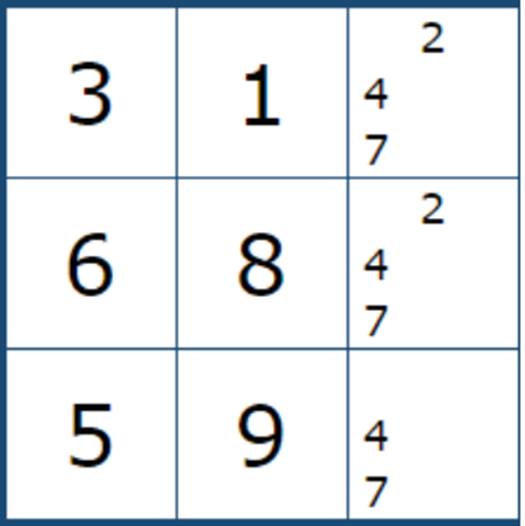
그렇다고 무작정 찾기 보다는 게임을 풀다가 아래 그림들과 같이 

1개의 하우스안에 확정숫자가 6개가 되고, 남는 3개의 칸에서 확정된 트리플 형태가 나오면 눈으로 익히는 것을 추천한다. 

 

확실한 트리플 332 형태 XYZ / XYZ / YZ

확실한 트리플 322 형태 XYZ / XY / YZ

확실한 트리플 322 형태 XYZ / XY / XZ

 

확실한 트리플 322 형태, XYZ / XY / XZ

 

확실한 트리플 222형태 XY / XZ / YZ

 

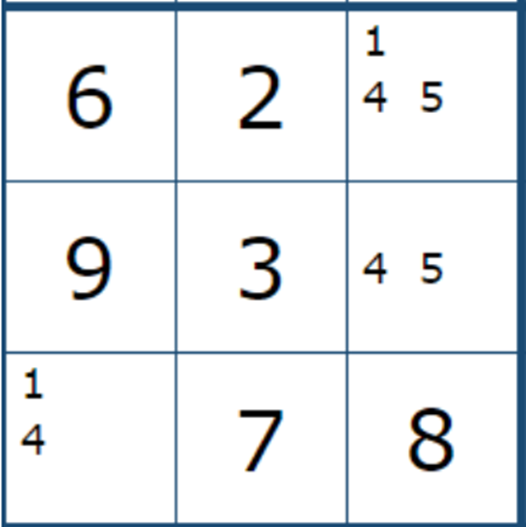
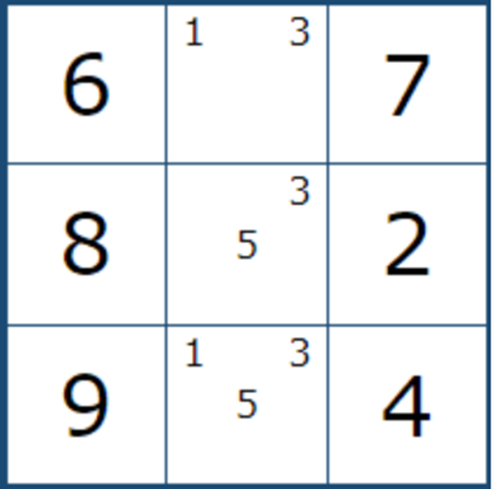
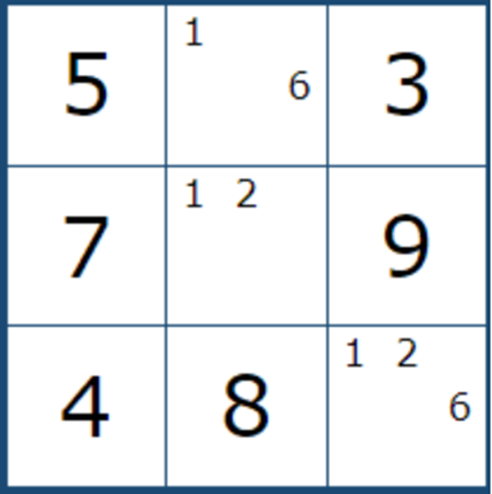
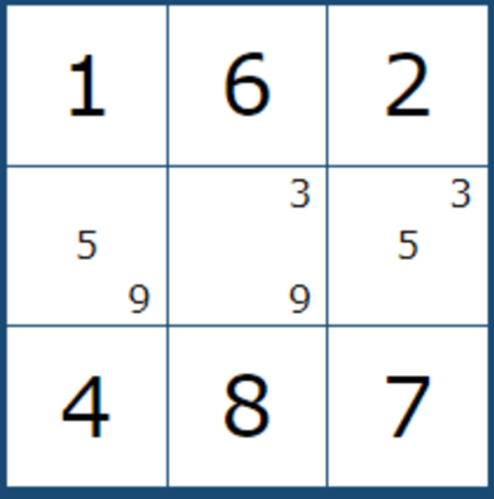
11월 6일 추가... 최근에 XY 체인 공식이라는 것을 공부하는데, 확실한 페어 및 트리플을 잘 보는 것이 매우 중요하다는 것을 느끼고 있던차에 아래와 같이 페어. 트리플, 쿼드가 다발로 나오는 판에서 많이 헤멨다.

 

 

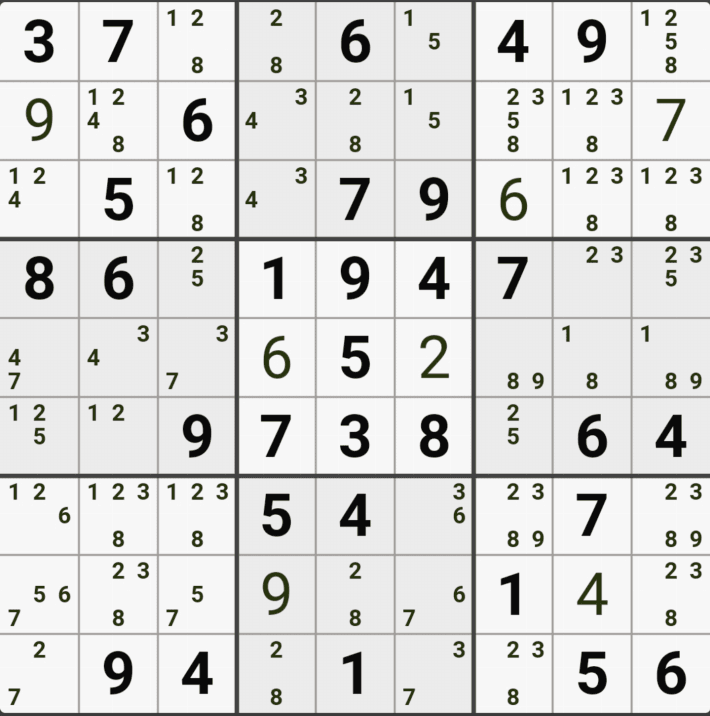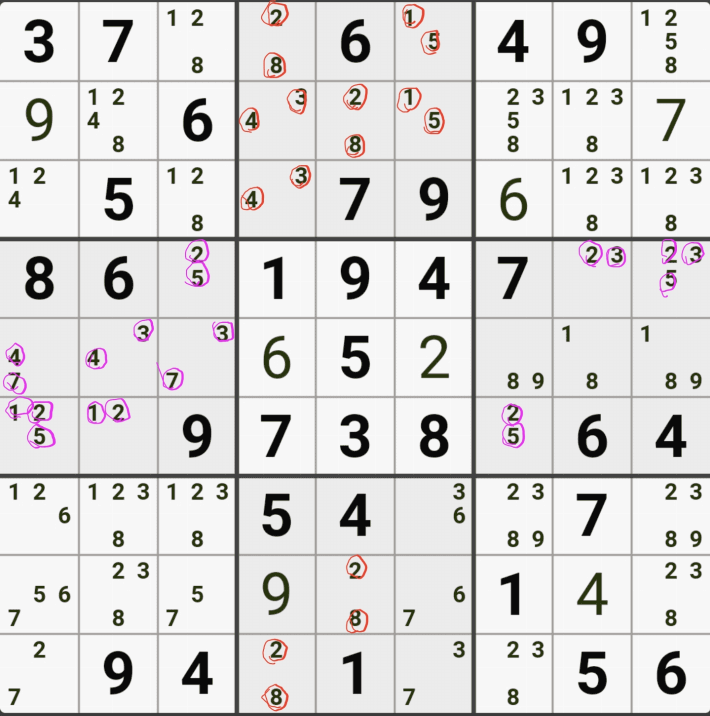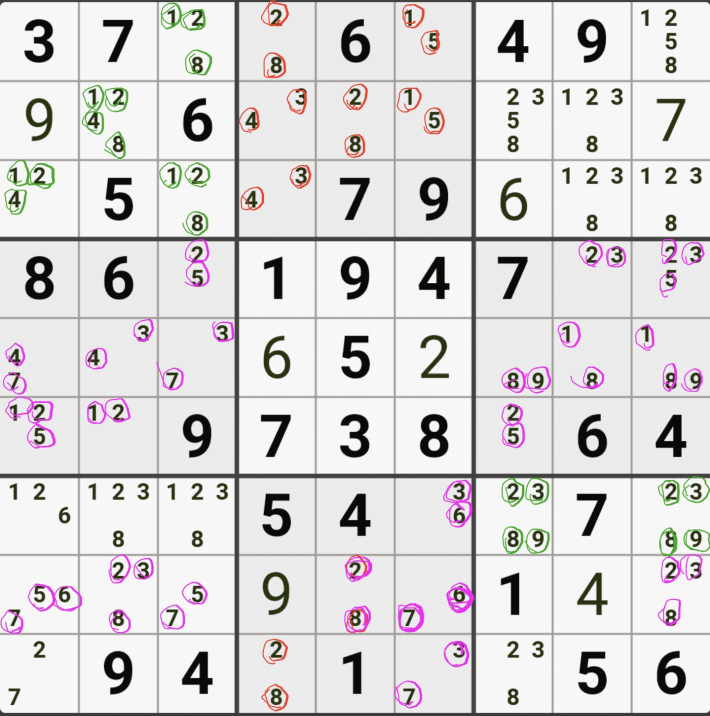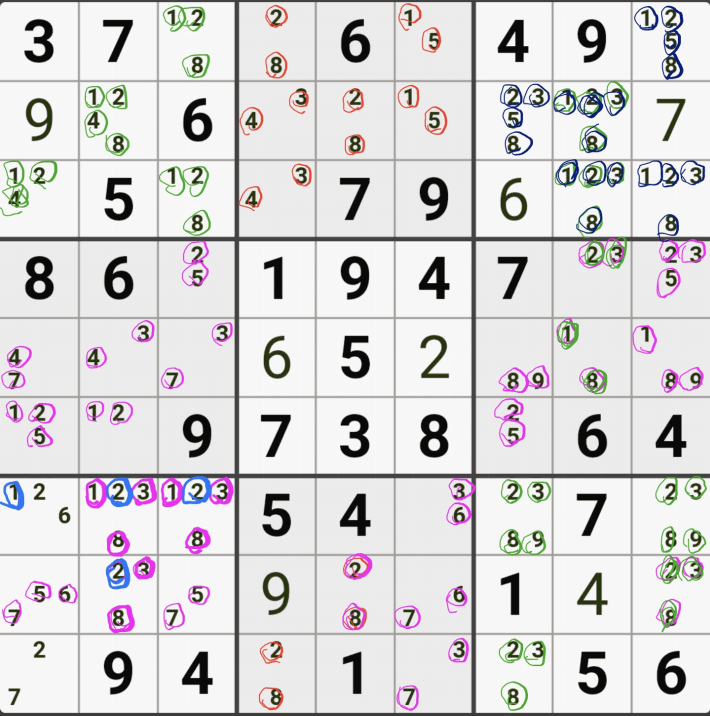
3. 숨겨진 트리플(Hidden Triple)

 

 명칭에서도 엿보이듯이 '확실한 트리플'이 다른 후보수에 둘러 쌓여져서 찾기가 좀 어려운 XYZ+@의 형태로 움짤로 먼저 보자.

 

 

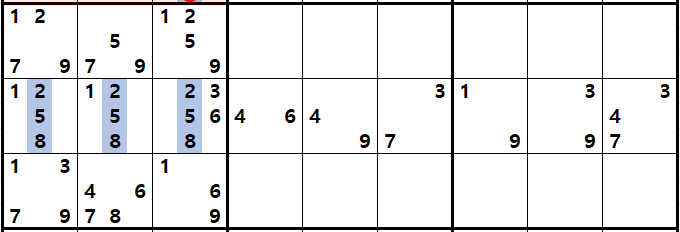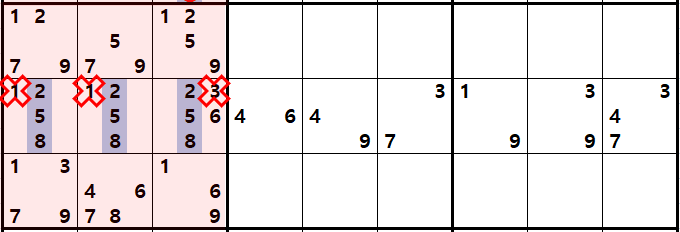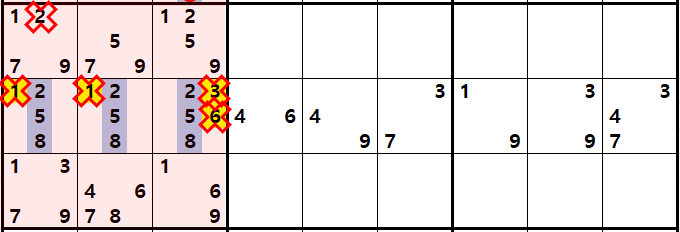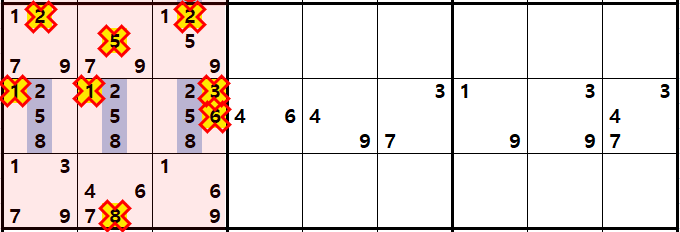
 위와 같이 하우스안에 3개씩 남은 숫자가 조합된 숨겨진 트리플 주위에 있는 다른 후보숫자들을 지우면 확실한 트리플로 변환된다. 

 

 위의 움짤은 이해를 돕기 위해서 숨겨진 트리플을 에워 싸는 다른 후보숫자를 적게 넣었는데

 

 

실전은 우측 7열~9열이 숨겨진 트리플이다. 개인적으로는 굳이 숨겨진 트리플을 찾고자 노력하지 않는 것이 맞다고 생각한다. 다만

 

1. 하우스에 후보숫자가 4~5칸 정도 남은 상황 (암산으로 커버 가능한 범위라고 본다)

2. 숨겨진 트리플 같은데, 위의 예제 처럼 주변에 붙은 후보수가 1~2개인

 

 상황에서는 츄라이 해보는 것을 추천한다. 

 

 그래도 패턴을 익혀보라고 '스도쿠 솔브' 사이트에서 예제를 좀 가져 왔다. 아래 더 보기를 누르면 된다. 

 

 

그러나 숨겨진 트리플을 정복하고픈 스도커가 있을 것이다. 

 

100% 확률은 아니지만 숨겨진 트리플을 잘 찾는 방법이 있다. 

4칸이 남은 상황에서는 99% (5~6칸 상황에서는 대략 80%) 확률로

숨겨진 트리플을  찾을 수 있는 방법이 있는데

 

 

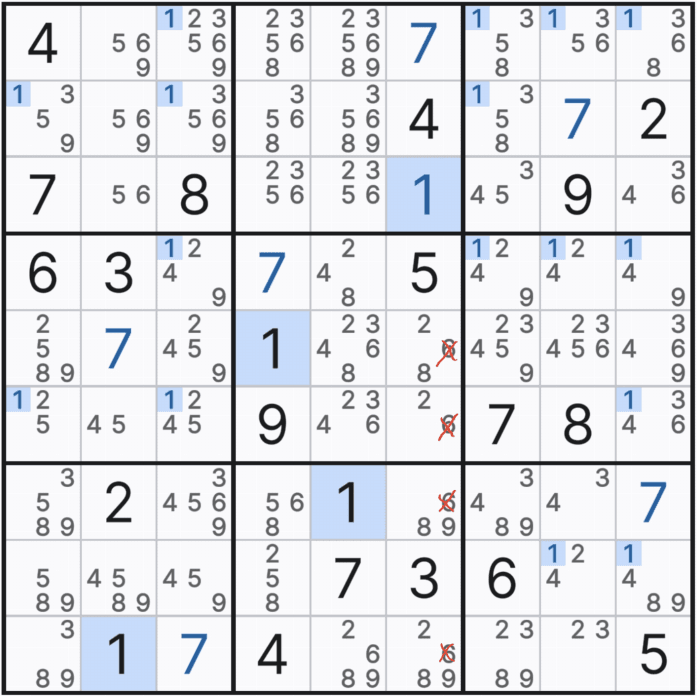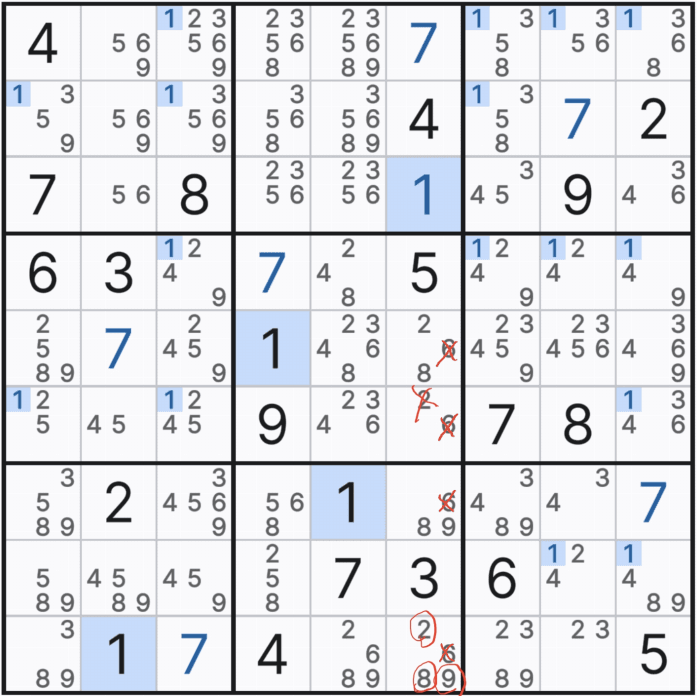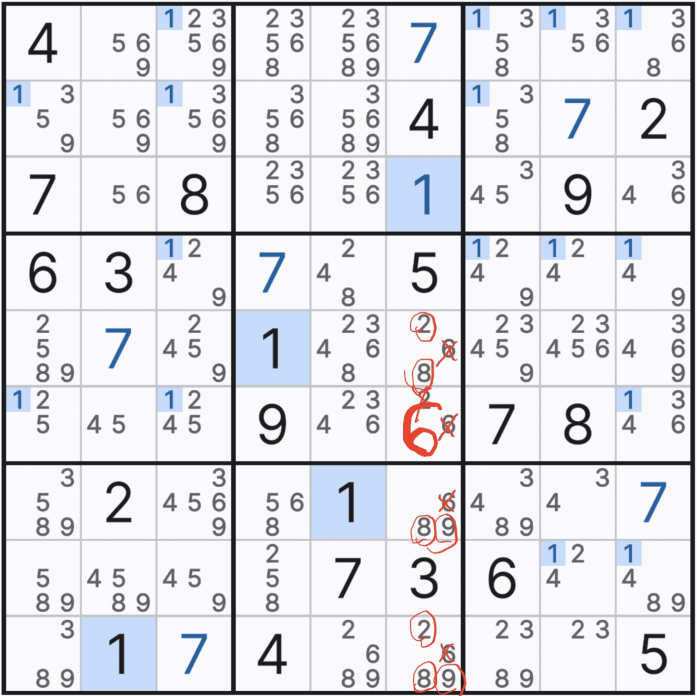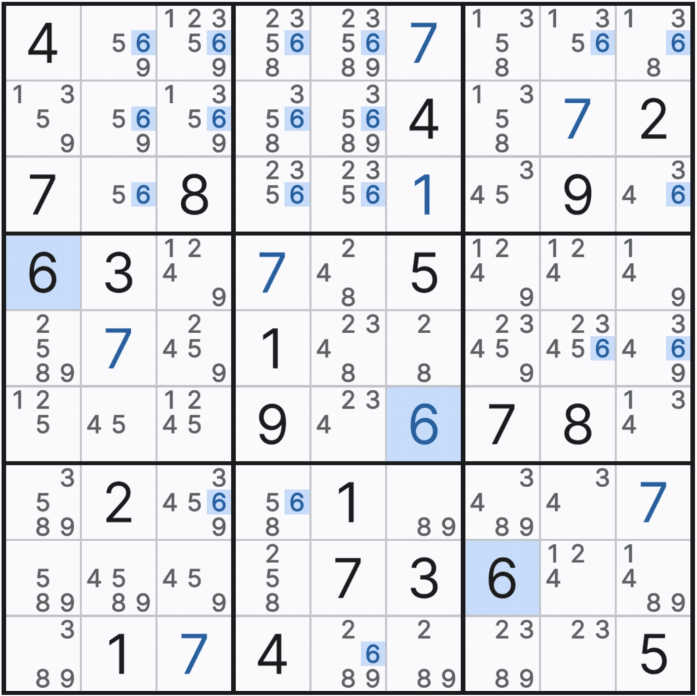
 위의 움짤과 같이 4개가 있는 후보수 6을 지우고

 트리플을 이루기 위해서는 최소한 2개의 후보수가 필요하므로

 후보수 1개 남는 칸의 2는 버리고 

 

 남은 3칸에서 트리플 숫자 28 / 89 / 289 (XY / YZ / XYZ - 322)로 트리플이 되는 것을 알 수 있다. 

 또한 트리플을 이루는 칸에 위와 같이 6의 다른 숫자가 1~2개 끼는 문제가 되지 않는다.

 

11월 6일 추가 숨겨진 트리플 찾기 예제 (아래 더 보기 클릭)

 

 

 

 

 

 

 4칸 남은 상황에서 숨겨진 트리플 찾기가 실패하는 1%의 경우는

 선행되는 다른 공식 적용이 되지 않았을 때이다. 

 

12월 1일 추가 > 최근에 'Andoku 스도쿠 3'이라는 앱을 유료결제하고 난 후, 좌절을 맛보고 있다. 레벨이 1~9단계까지 있는데, 스도쿠를 조금 알게 됐다고 생각하고 9단계를 풀다가 막혀서 못 푸는 문제가 70%는 되는 것 같은데 돌파구를 '숨겨진 트리플 찾기'에서 찾았다. 내용은 아래 더 보기를 클릭하자. 

 

 위에서 언급한 좌절의 이유는 XY체인이나 AIC 등의 체인 때문이 아니고, 아래 움짤처럼 1판에 연속해서 3~4개 나오는 사시미or핀드 > 소드(젤리)피쉬 때문이다. 

 

움짤예제1. 동일한 판에 후보숫자 4에

핀드 소드피쉬 > 사시미 소드피쉬 > 사시미 젤리피쉬 

3개 출현

 

1번 핀드 소드 피쉬로 4[E5], 4[E6] 제거

2번 사시미 소드피쉬로 4[E4] 제거

3번 사시미 젤리시퓌로 4[F5] 제거

 

 난이도가 높은 판은 위의 움짤처럼 초반 풀하우스 제거를 해도 후보숫자가 1개 정도 남기고 많은 후보숫자가 남아서

핀드>사시미 피쉬종류가 많이 나오는 편인데 생각보다 찾기가 어렵다. 

 

 그래서 막힐 때마다, 그룹 체인으로 타계하려고 하지만 이 또한 쉽지 않다.

 

 그러다가 한 가지 돌파구로 숨겨진 트리플 찾기가 생각나서 적용해 봤는데, 대체적으로 효과가 있는 것 같다. 

 

움짤예제 2. 위의 움짤과 동일한 상황에서 핀드>사시피 피쉬를 '숨겨진 트리플 찾기'로 돌파 

시간 단축을 위해 후보숫자 4가 4칸에 들어 있는 하우스만 조사.

 

 

움짤예제1.에서는 3회의 피쉬공식을 사용하여

4[E5], 4[E6], 4[E4] 및 4[F5]를 제거 했는데, 

 

똑같은 상황에서 '숨겨진 트리플 찾기'로 

 

2번째 찾기에서 후보숫자가 4개인 4를 배제한 후 1개만 남는 후보숫자 2[D4]도 배제하고 남은 숫자에서 2/4/8이 숨겨진 트리플로 존재 하는 것을 확인하여 4[D4]를 확정하고,  

4[E5], 4[E6], 4[E4] 및 4[F5]뿐만 아니라

 

박스5와 D행 및 4열에 있는 모든 후보숫자 4를 지우는 것을 알 수 있다. 

 

또한 이번 예제는 후보숫자 4가 4개인 하우스만 조사했는데, 대체적으로는 어디에서 확정 가능한 '숨겨진 트리플'이 나올지 모르기 때문에 A>H행, 1~9열, 박스1~9의 순으로 조사하고 만약에 숨겨진 트리플을 찾으면 우선 서칭을 중단하고 후보숫자 제거 또는 확정을 짓고 그 다음 '숨겨진 트리플'찾기를 이어가야 한다. 탄력 받아서 여러 개의 '숨겨진 트리플'을 찾아서 결과에 따라 확정 또는 제거 시 서로 간섭하는 숫자 때문에 오답이 나올 확률이 99%다. 

 

Andoku 스도쿠 3 - 강력 스도쿠 추천 앱

Andoku 스도쿠 3 - 강력 스도쿠 추천 앱