움짤로 익히는 스도쿠 2. 후보숫자 넣기 및 링크의 개념 익히기
- 스도쿠/초급
- 2024. 10. 15.
지난 글에서 스도쿠의 개념 및 풀하우스 채우는 방법을 알아 봤는데 이번 글에서는 링크 (=후보수 X의 연결 상태) 에 대해 자세히 알아보도록 하겠다. 제목은 링크의 개념이지만 기초 공식에 관한 사항도 좀 나온다. 링크는 모든 공식을 아우르는 단어라고 보면 된다. 간단하게 후보숫자를 넣는 방법은 아래 움짤을 보면 되겠다.
12월 10일 추가 > 최근에 Andoku 스도쿠 3이라는 앱을 유료결재 했는데, 풀이과정을 다이아그램으로 풀어줘서 매우 좋다. 일단, 몰라도 한 사이클만 보고 밑에 설명을 보면 좋을 것 같다.

위의 움짤을 초반에 일부분(2~3개의 연속된 숫자)만 후보숫자를 채우고, 중반에 각 숫자별로 후보숫자를 다 채우면서 푸는 움짤도 만들어 봤다. 쭉쭉 보고 넘어 가자!

1. 보통 스도쿠가 시작하면 아래와 같이 머리속에 가상의 선을 그으면서 다이렉트로 풀하우스(=마지막 숫자) 찾기를 진행한다.
2. 그러다가 보면 어느 순간에 암산으로 풀하우스 찾기가 막히는 경우가 생기는데, 이 때부터 쓰는 기능이 후보숫자를 노트하는 기능을 사용한다.

위의 움짤과 같이 종이에 메모하듯이 스도쿠 칸안에 작은 숫자로 노트를 하는 것을 '후보수 넣기'라고 한다. 기본적으로는 풀하우스 찾기와 마찬가지로 박스에 있는 찾고자 하는 확정숫자 X 및 박스내에 있는 W, Y, Z 등의 확정숫자를 참고하여 빈칸에 후보숫자를 노트한다. 후보숫자의 배열에 따라 우리가 보고 익히게 될 X윙, Y윙, 숨겨진 트리플, 소드피쉬, 젤리피쉬, X체인 등등의 모든 공식을 적용하는 단서가 된다.
따라서 이 후보숫자 없이 풀하우스 찾기와 후보수를 정확하게 노트하는 것이 스도쿠를 잘 하는 첫걸음이라고 보면 된다.
풀하우스 찾기와 후보숫자 기입하기는 동일한 방식이나 다른점은 풀하우스는 마지막 숫자를 찾아서 답을 확정하는데, 반해서 후보숫자 노트는 2개 이상의 확정숫자 가능한 칸에 숫자를 넣는 것이다.
후보숫자 넣는 방식
1. 움짤1과 같이 풀하우스를 찾다가 막히는 순간부터 움짤2처럼 후보숫자를 찾는 방식이 기본적으로 행하는 방식이다. 후보 숫자는 처음에 주어진 확정숫자가 많은 번호부터 공략하는 것이 확정숫자를 빨리 많이 찾는 기본이다. 이는 후보숫자를 가산법으로 채워나가면서 다른 풀하우스를 찾아 확정숫자를 바꾸는 방식이다.
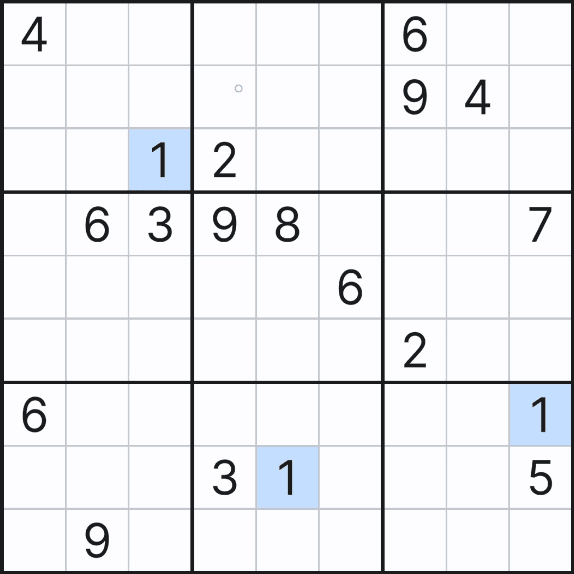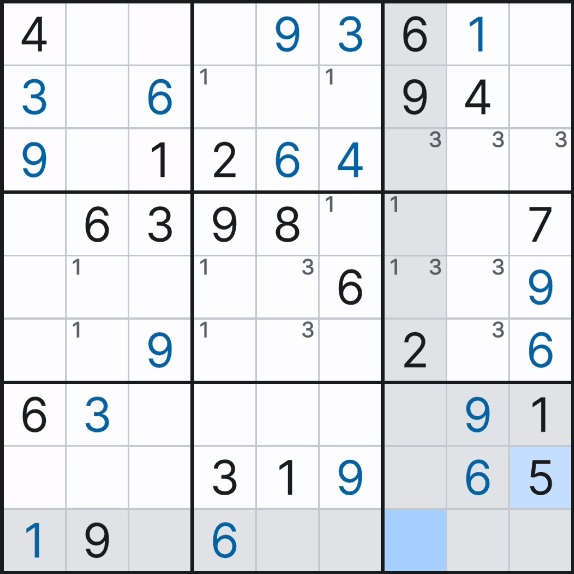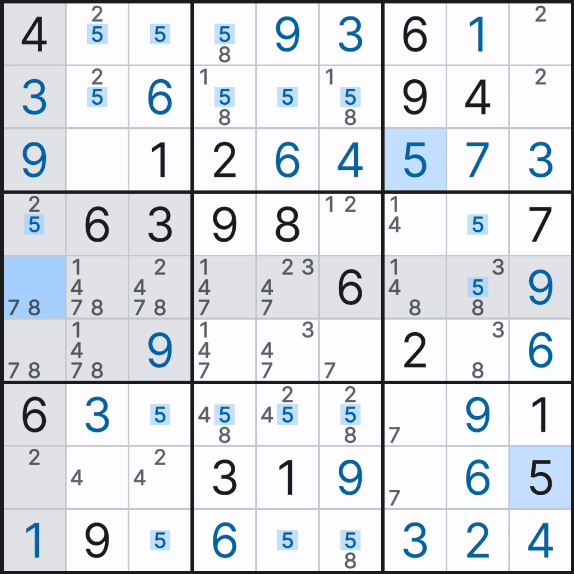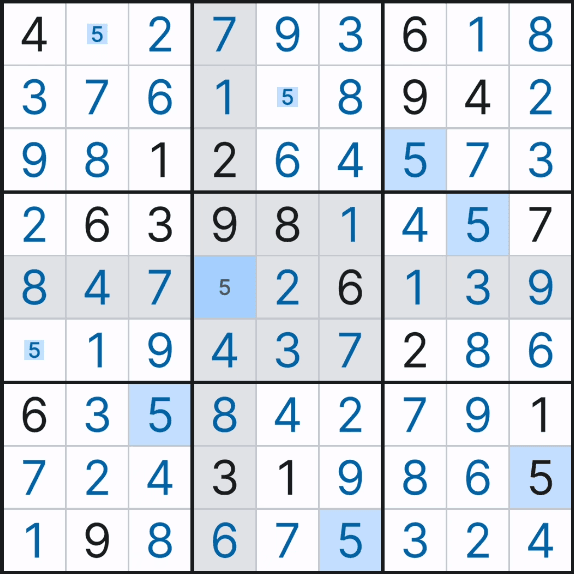
2. 아래 그림과 같이 후보숫자를 모두 다 입력한 후에 감산법으로 숫자를 지워 나가며 풀하우스를 찾아 확정하는 방법이 있다. 처음에 모든 후보숫자를 기입하는데 어려움이 있지만 완벽하게 채우면 가장 쉽고 빨리 풀어 나갈 수 있는 방법이다. (나중에 배우겠지만 모든 후보숫자를 채워 놓으면 아래와 같이 (3,2)칸의 8, (4,8)칸의 5 처럼 '풀하우스'가 반드시 나타나게 되어 있다.)
3. 스도쿠를 풀어가는 또 다른 방식은 위의 1과 2를 절충해서 시작부터 암산과 메모를 병행하면서 풀하우스를 찾아가는 방식이다.
4. 이외에도 박스1부터 후보숫자 채우기, 1행부터 채우기, 1열부터 채우기등 다양한 방법이 있는데 풀어 나가는 방식은 본인이 게임을 진행하다가 제일 편하고 재미있는 쪽으로 정하면 되겠다.
이제 본격적으로 링크에 대해 알아보자. 스도쿠의 모든 숫자는 후보수와 링크로 시작해서 링크로 끝난다고 보면 되겠다.
후보숫자에서 바로 링크 설명을 하는 것이 빨라 보일 수도 있지만, 나도 다른 사이트에서 간략하게 설명하는 공식만 보며 스도쿠를 배우다가 고급 기술인 '체인 공식'을 접하다 보니까 제일 기본으로 알고 있어야 할 개념이라고 생각을 하게 됐다.
링크란 무엇인가?
링크는 풀하우스가 되는 숫자 X외에 2개 이상의 숫자 X가 상호 영향을 주며 연결되는 것이라고 보면 되겠다. 아래 링크의 종류 및 개념은 훑어만 보고 정확한 뜻은 좀 더 밑에서 움짤 예제를 보며 정확히 이해하도록 하자!
1-1. 스트롱 링크 - 한 개의 하우스 안에 후보숫자 X가 A, B - 2칸에만 들어 있는 숫자의 연결로 숫자 구성은 XY - XY, XY - XZ, XY - XW 등 다양한 형태로 위치한다. 즉, 한칸이 X 면 다른 칸은 X가 아니고, 한칸이 X가 아니면 다른 칸은 X가 된다는 뜻이다.
1-2. 이중 위치 링크 - 스트롱 링크 중에서 A, B 칸에 숫자가 XY - XY 2가지만 존재하는 경우 A가 X면 B가 Y가 되고, A가 Y면 B는 X가 되는 링크로 '이중 위치' 링크라고 한다. 이런 이중 위치를 갖는 링크는 '확실한 페어(Naked Pair)'라는 타이틀로 불리며 박스 또는 행과 열에 대한 강력한 힘을 갖게 되기도 한다. 그 강력한 힘 중에 하나는 위크링크의 상황으로 보여도 '이중 위치'링크는 언제나 스트롱 링크로 취급 되다는 것이다.
아래 그림은 이중링크 배열이다.

위의 말을 다시 한번 개념 정리를 하면 XY-XZ의 형태는 X에 대해서만 스트롱 링크가 되는 것이고,
XY-XY 형태의 스트롱 링크는 X 및 Y에 대한 무조건적인 스트롱 링크가 되는 것이다.
2. 위크 링크 - 한 개의 하우스 안에 숫자 X가 3칸 이상 들어 있는 숫자의 연결로 3칸에 들어 가는 숫자는 최소한의 숫자 X,Y,Z 3개가 들어가고 XY, XZ, YZ, XYZ 형태로 존재하고 3개를 초과하는 후보 숫자가 들어 갈 수도 있다. 이는 A, B, C 칸의 조건에 따라 A가 X가 아니면 B 또는 C가 X가 되는 조건부 링크라고 보면 되겠다.
3. 그룹 링크 - 후보숫자 X가 한 하우스에 3개 이상 존재 하지만, 하우스 중에서 박스안에만 존재 하는 경우 연속되는 2개, 또는 3개의 숫자는 단일 갯수로 취급하는 경우가 있다. 고급 기술로 넘어 가면 그룹 링크를 이용한 체인 전략 구사가 된다.
후, 역시 글로 스도쿠를 이해가기란 어렵다. (설명하기도 어렵다.)
여러분이 들어 봤을 만한 X윙, Y윙, 소드피쉬, 젤리 피쉬, 숨겨진 트리플 등 많은 전략들은 이 링크들의 관계가 특정화된 공식이라고 보면 되겠다. (A^2+B^2=C^2 이라는 피타고라스의 정리 처럼 말이다.) 그럼 이 2개 이상의 숫자가 링크되는 형태는 어떤지, 서로 연결되면 무슨 일이 생기는지는 실제 스도쿠를 푸는 움짤을 보며 설명해 나가도록 하겠다.
나의 스도쿠 풀기 스타일은 위에서 언급한 3번 초반부터 풀하우스 찾기 및 보조역할인 후보수 넣기를 혼합으로 사용한다. (공식을 익힐 때는 모든 후보숫자를 넣고 게임을 풀어간다.)
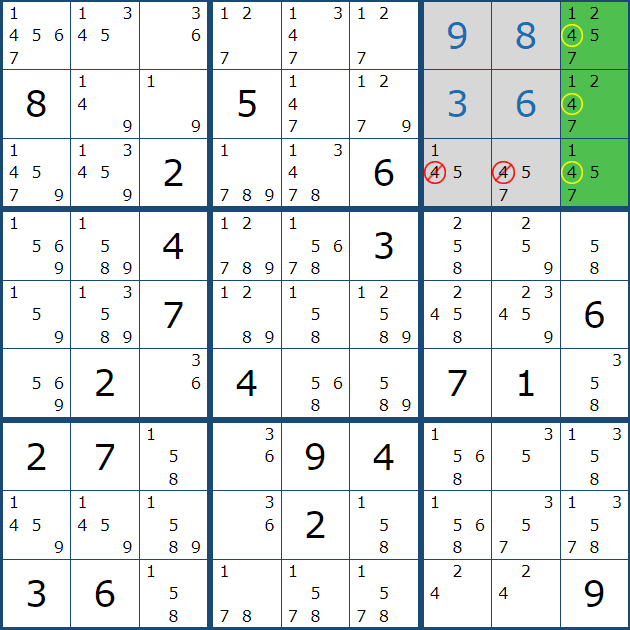
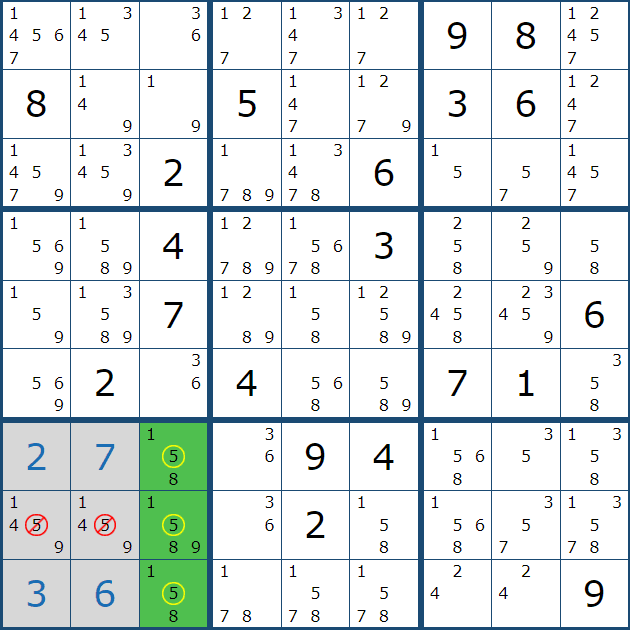
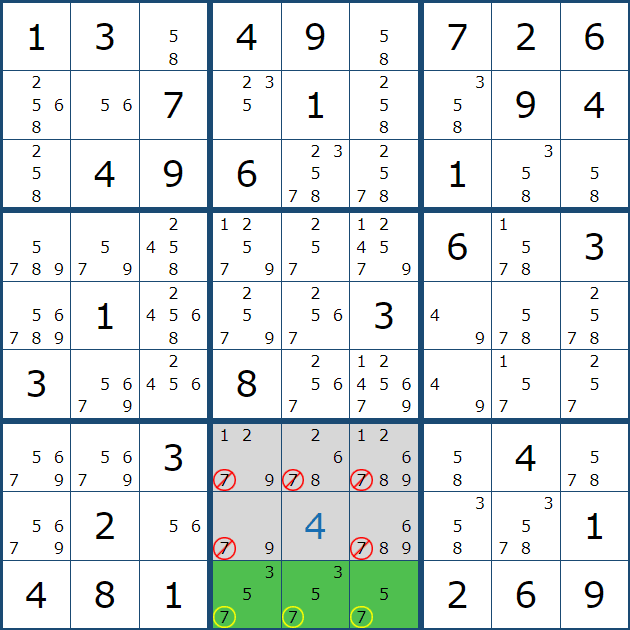
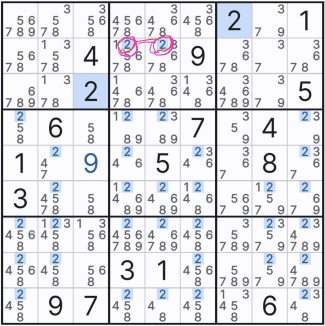
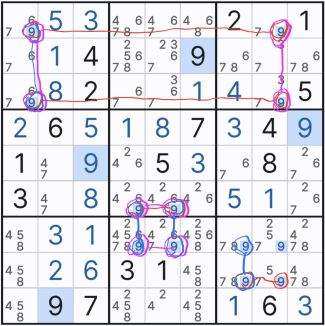
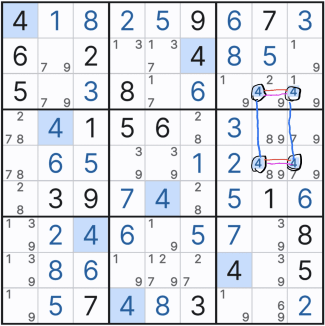
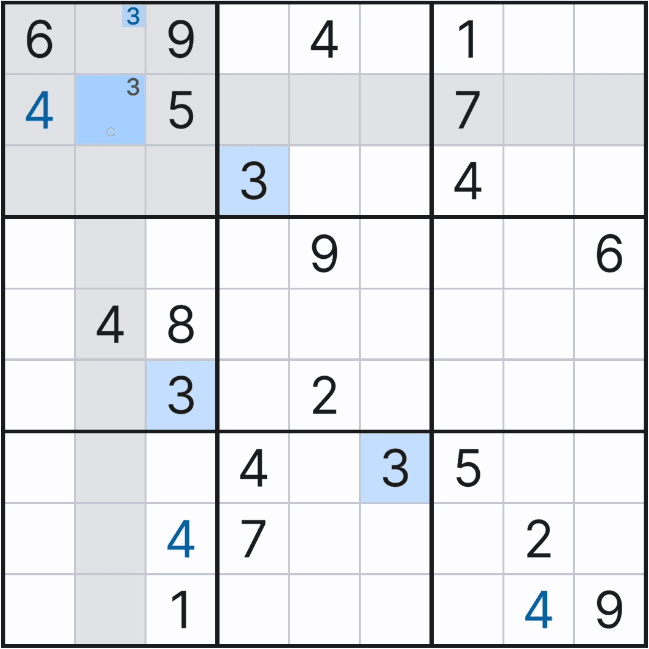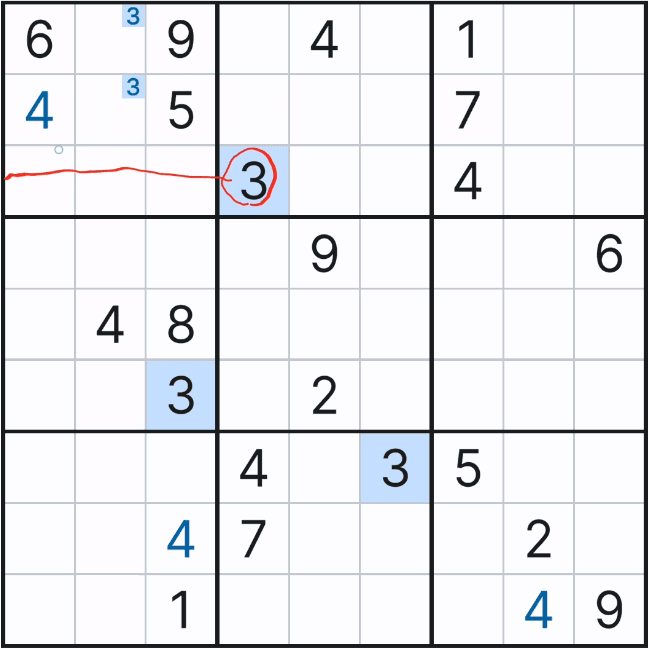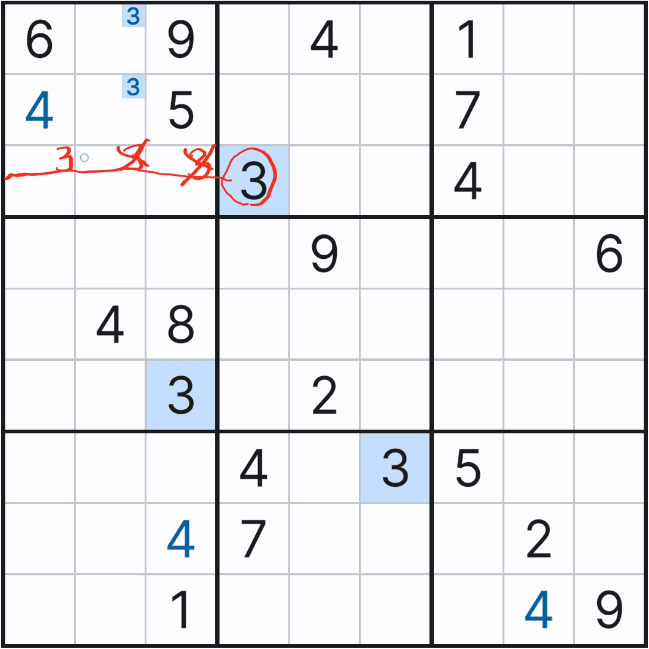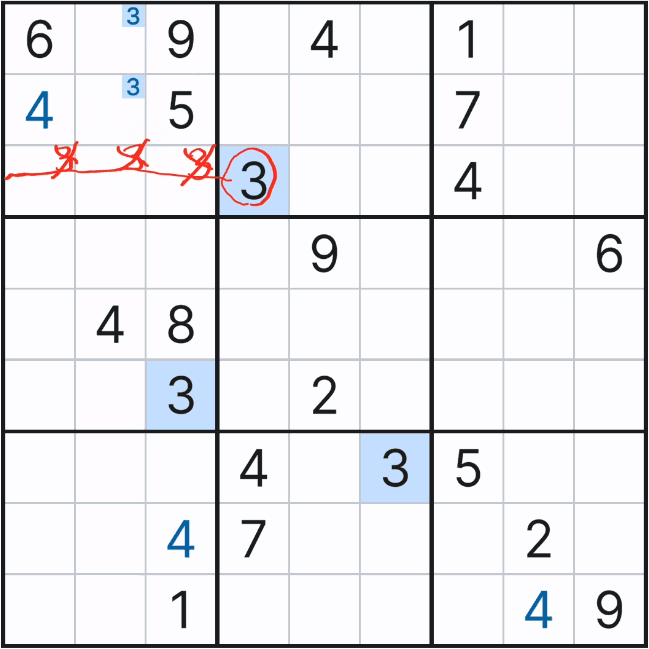
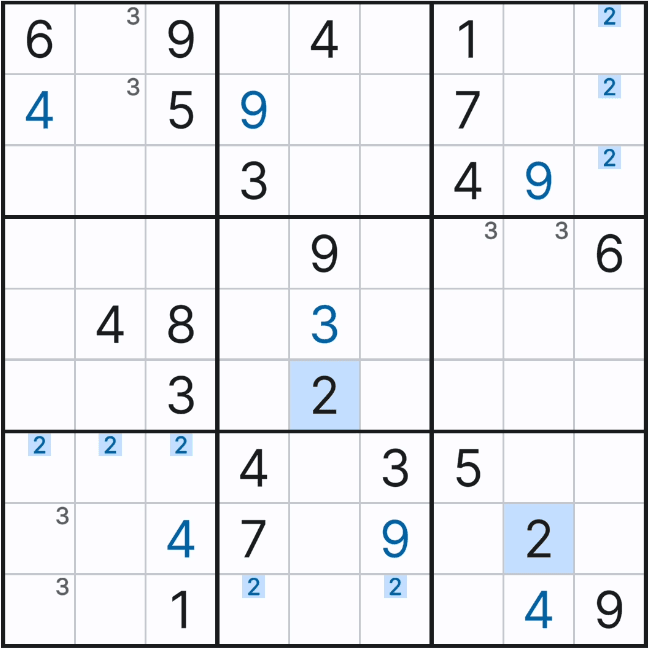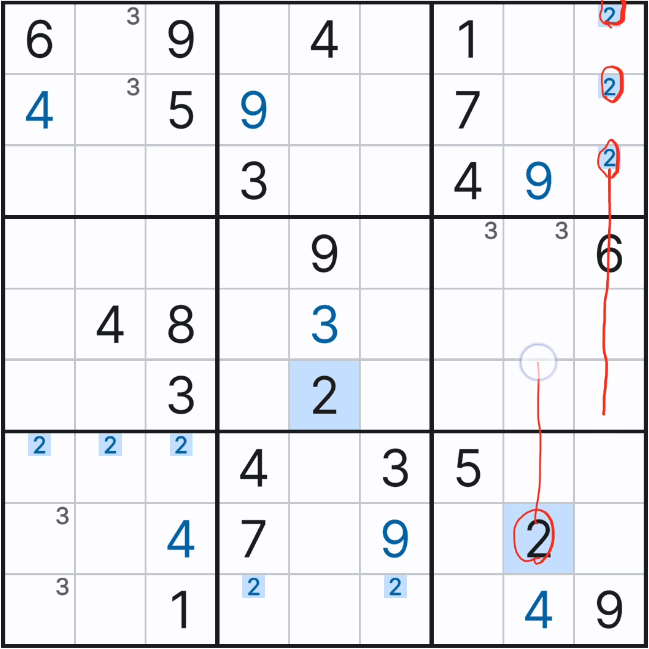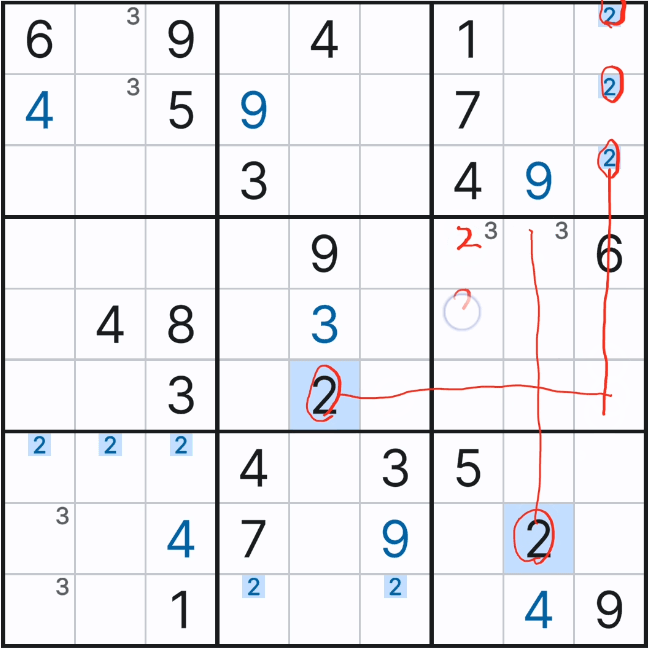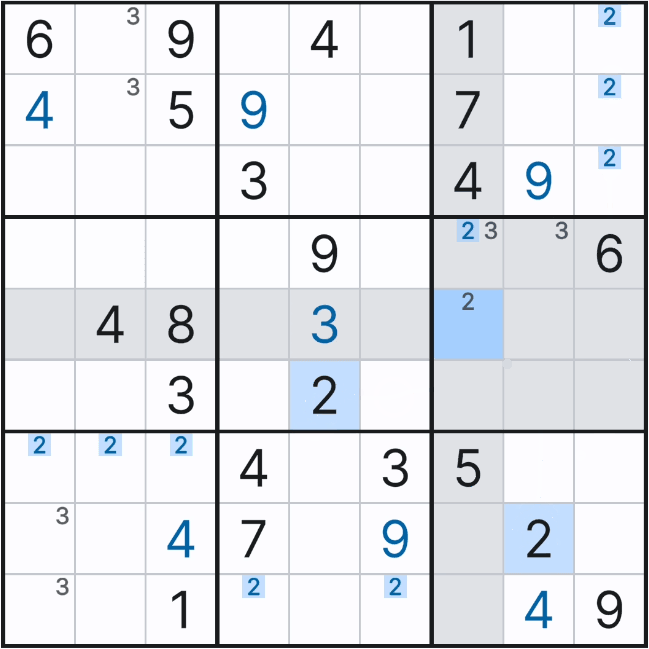
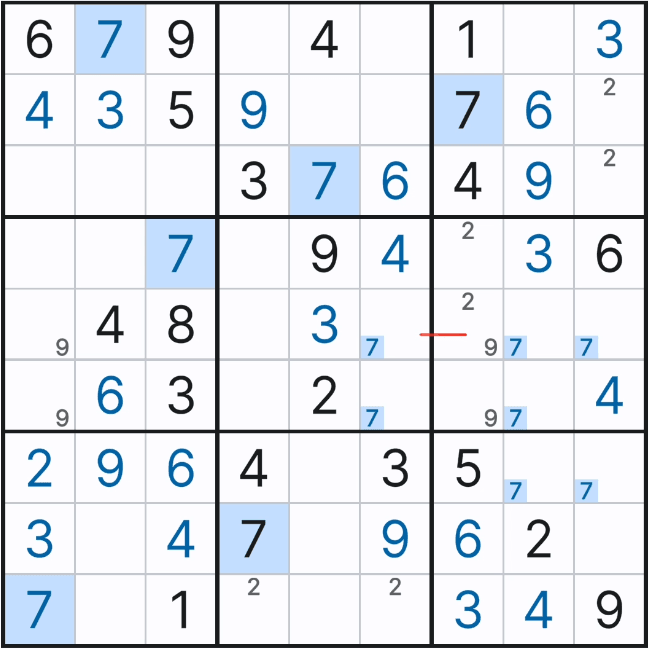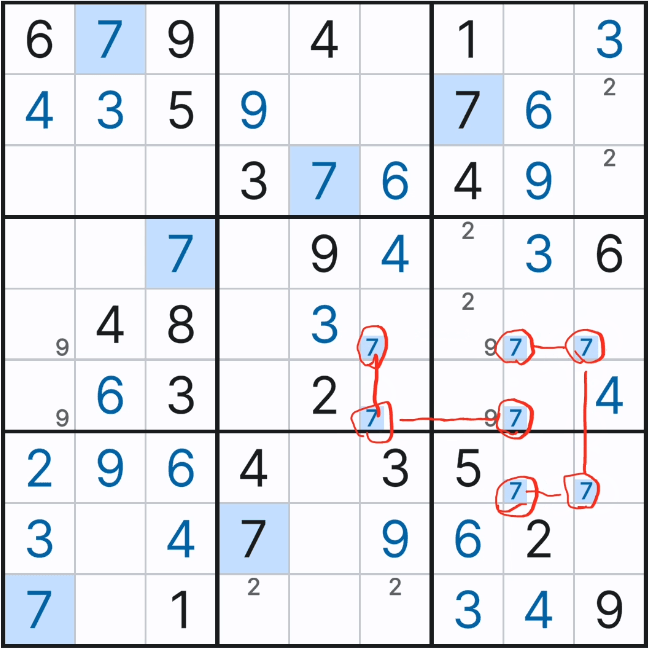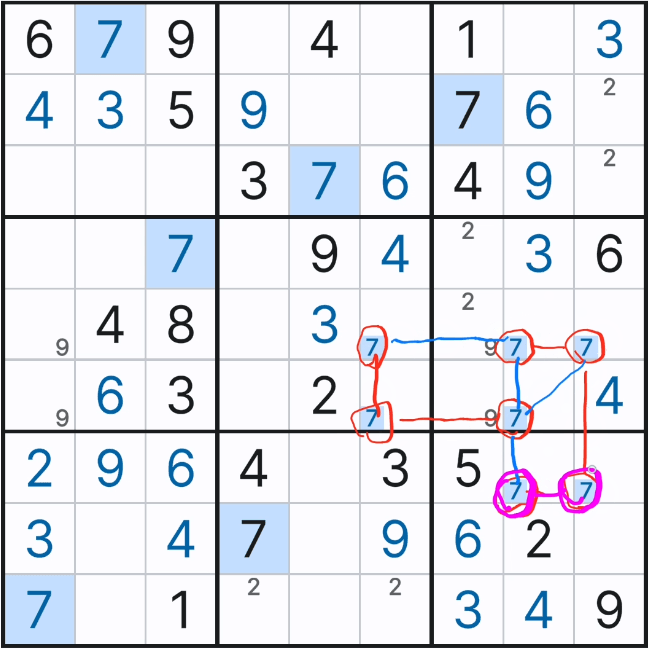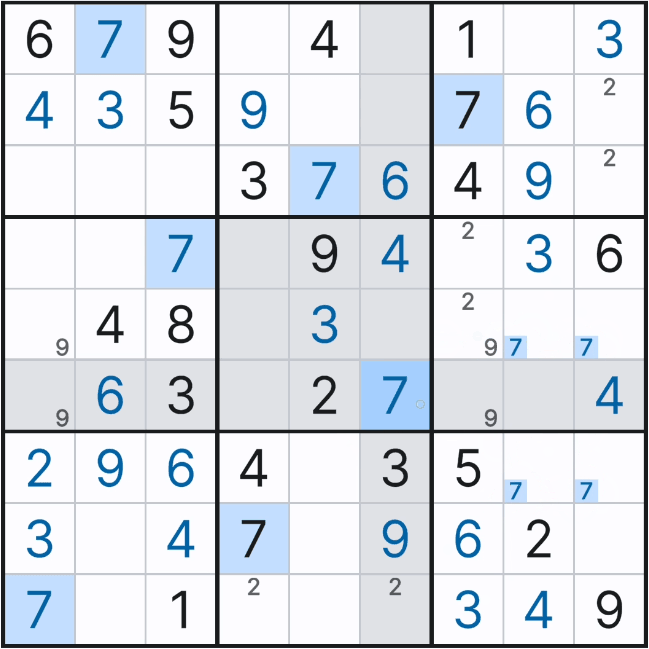
1. 스트롱 링크와의 만남.. 아래와 같이 주어진 확정숫자 갯수가 4개나 있는 4에 대한 풀하우스 찾기를 하다가, 다음 숫자 3에서 처음으로 박스1에 첫 후보숫자 3 두개를 채웠다.

2. 그 후 아래의 움짤과 같이 박스7에 3을 확정숫자로 기입했는데.... 스도쿠를 좀 풀어본 사람들은 뭔가 위화감을 느낄 수도 있을 것이다.

2열 8과 9행에 후보숫자 3 기입이 빠진 것 처럼 보인다.
이렇게 기입한 이유는 박스1의 후보숫자 3의 '스트롱 링크'에 의한 것인데 움짤로 보자..

위의 움짤을 보면 박스 1의 연속된 후보숫자 2개를 빨간색으로 칠하는 것을 볼 수 있을 텐데, 초장에 언급한 스트롱 링크 중에서도 '이중 위치'링크이다. 이 말은 2열에서는 후보숫자 3이 (1,2) 또는 (2,2) 칸 둘 중 한칸에만 존재할 수 있다는 의미이다.
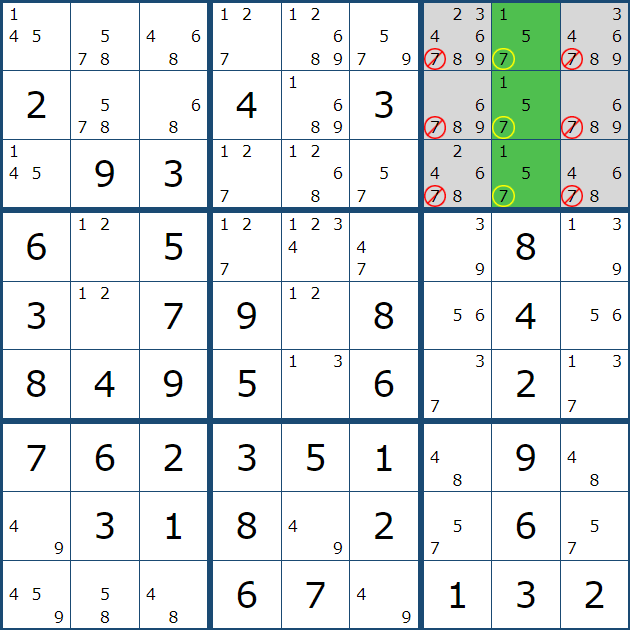
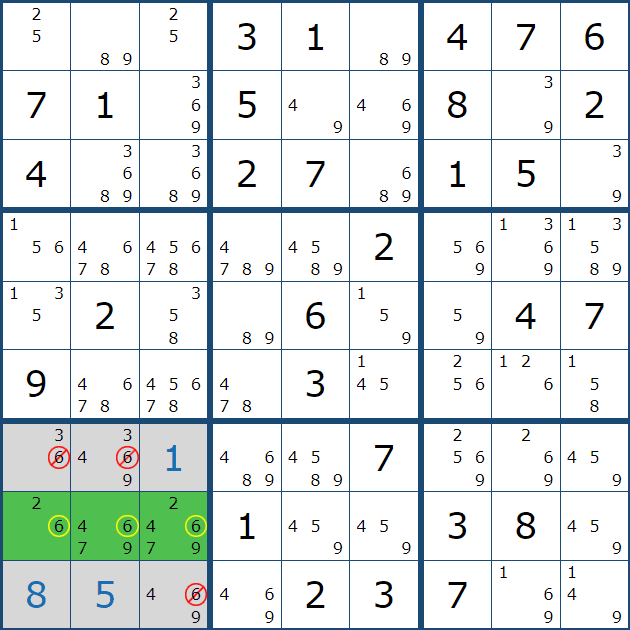
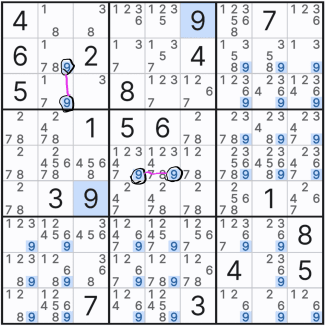
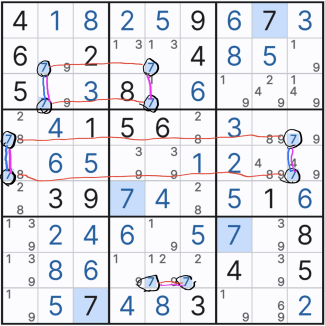
이 말을 다시 움짤로 만들면 아래와 같이
3행에 있는 확정숫자 3으로 인해
(1,2) 또는 (2,2) 2칸 중에 하나에만 후보숫자 3이 확정숫자가 될 수 있다는 의미로,
좀 더 확장시키면 2열에서 3번은 7~9행에는 올 수 없다는 뜻이다.
이렇게 박스안에 후보숫자 위치가 특정되는 상황을 '잠긴 상태'라고 한다.
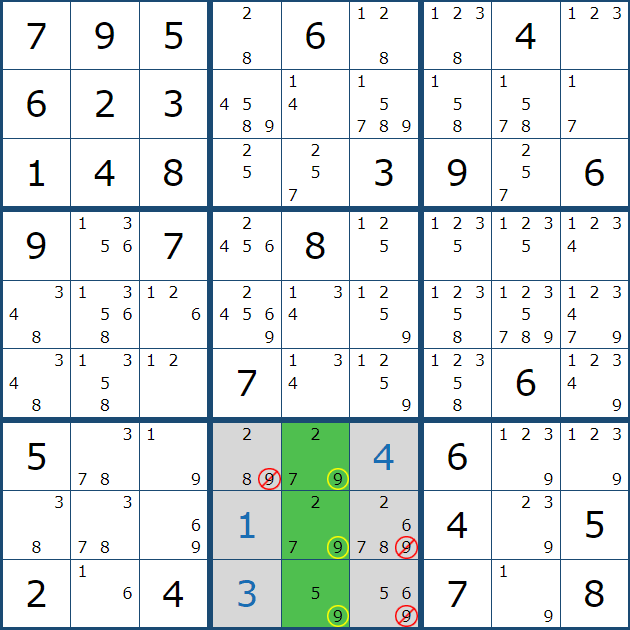
그래서 잠긴 후보숫자 3이 그룹링크가 되어 준 확정숫자 3의 역할을 담당하게 되는 것이다.
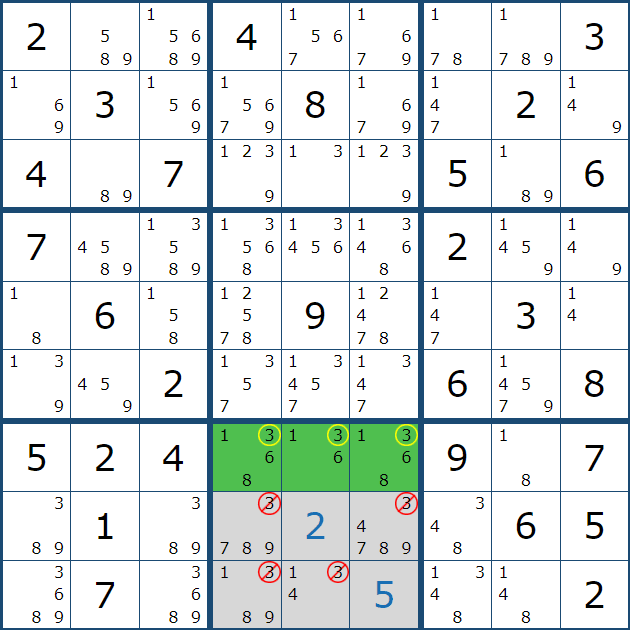
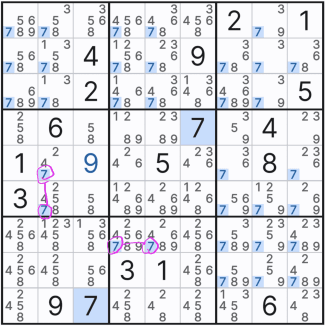
그래서 아래와 같이 셀 7에서 (7,1), (8,1), (9,1) 칸에만 후보숫자 3을 노트할 수 있었다.

이렇듯, 스트롱 링크는 명칭대로 강한 힘을 쓰는데 셀 안에 잠긴 숫자는 특히 강력하다. 이렇게 그룹 링크는 연속된 2개의 링크가 될 수도 있고, 아래와 3개의 연속된 위크링크 후보숫자도 박스에 잠기면 스트롱 링크와 같은 그룹 링크가 되어 힘을 발휘 하는 경우가 있다.
용어 2개 나온다~
페어 제거 (Pointing Pair )
박스 안에서 잠긴 연속된 스트롱 링크인 2개의 후보숫자 X는 그룹 링크가 되어 준 확정숫자의 역할을 할 수 있다. 움짤과 같이 같은 행과 열 뿐만 아니라 박스 안에 있는 후보숫자 X 또한 제거할 수 있다.
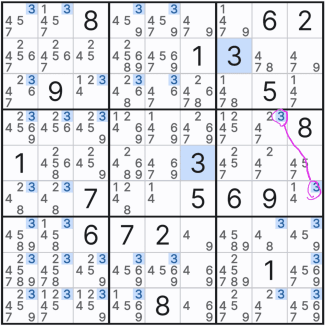
트리플 제거 (Pointing Triple)
박스 안에 잠긴 연속된 위크 링크인 3개의 후보숫자 X는 그룹 링크가 되어 준 확정숫자의 역할을 할 수 있다. 움짤과 같이 같은 행과 열 뿐만 아니라 박스 안에 있는 후보숫자 X 또한 제거할 수 있다.
아래는 트리픈 제거 패턴 모음이다. 행과 열 제거는 위의 움짤로 이해 했을거라 믿고 박스내에서 제거 되는 실제 예제를 보고 감을 잡자. 스도쿠는 고급 기술보다 기본 기술들이 초석이 된다고 보고, 놓치지 않도록 노력하자. 페어 제거도 같은 원리로 작동을 한다. 자료 출처는 '스도쿠 솔버'라는 사이트이다. 본인이 직접 문제를 입력할 수 있고, 체인 기술을 제외한 기본 공식으로 문제도 풀어 준다. 또한 글로만 나오는 것이 아니고 더 보기를 열면 알겠지만 다이아그램과 같이 풀어준다.
위의 페어제거 > 트리플 제거에 쓰이는 박스안에 동일후보숫자 2개 또는 3개가 연속되어 있는 배열을 그룹 링크라고도 부른다.
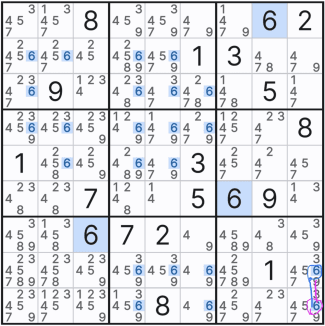
그룹 링크는 페어 or 트리플 제거처럼 다른 후보숫자를 지우기 위해서도 쓰지만, 아래 움짤 1행
체인이라는 공식을 쓸 때, 2~3개의 연속된 숫자를 한개의 숫자로 보고 On - Off를 적용하여 공식을 풀어나가기도 한다. 이때 그룹링크의 방향성은 연속된 숫자가 나열된 행 또는 열 한줄만 있다고 보면 되겠다.

실제로 그룹링크와 일반 링크가 혼재 할 때는 일반 링크의 방향을 따라간다고 보면 되겠다. 위의 움잘에서는 이해를 돕기위해 그룹 링크 중앙에 화살표를 긋었다. 아래 그림을 보면 이해가 더 쉬울 것이다.
확실한 싱글 (Naked Single) = 풀하우스 (Full House, 마지막 숫자)
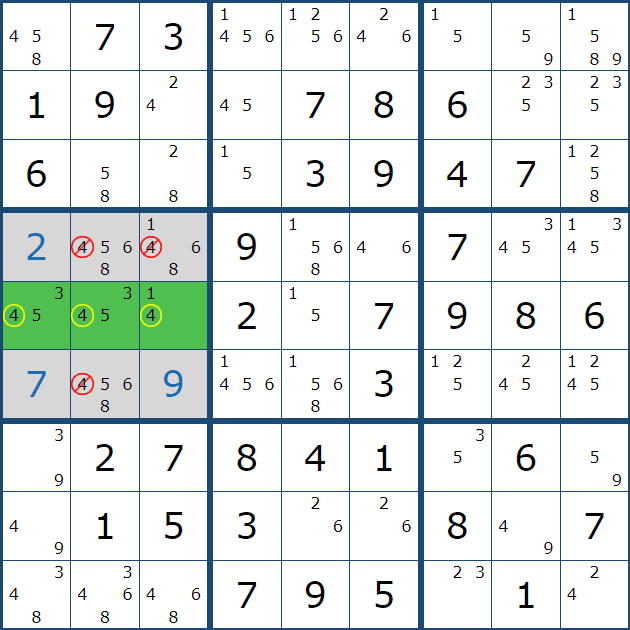
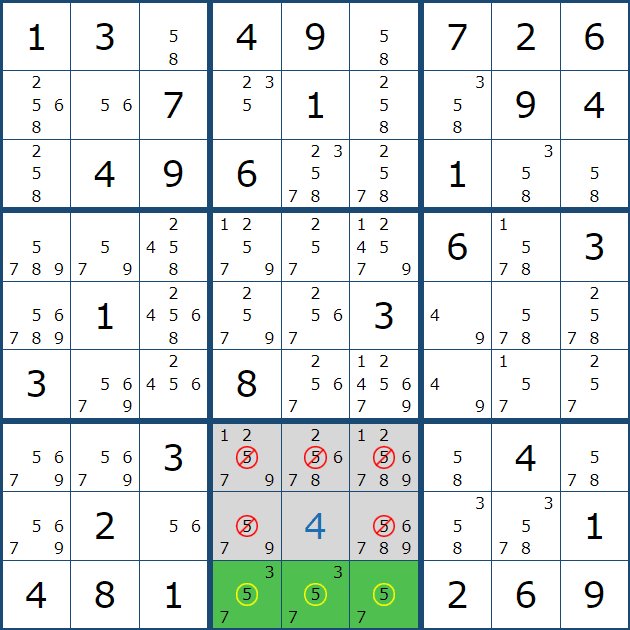
후보 숫자를 넣다보면 아래와 같이 풀하우스를 찾게 되어 확정할 수 있는데, 이렇게 후보숫자 X 가 1개만 남은 상태를 확실한 싱글' 상태라고 부른다.
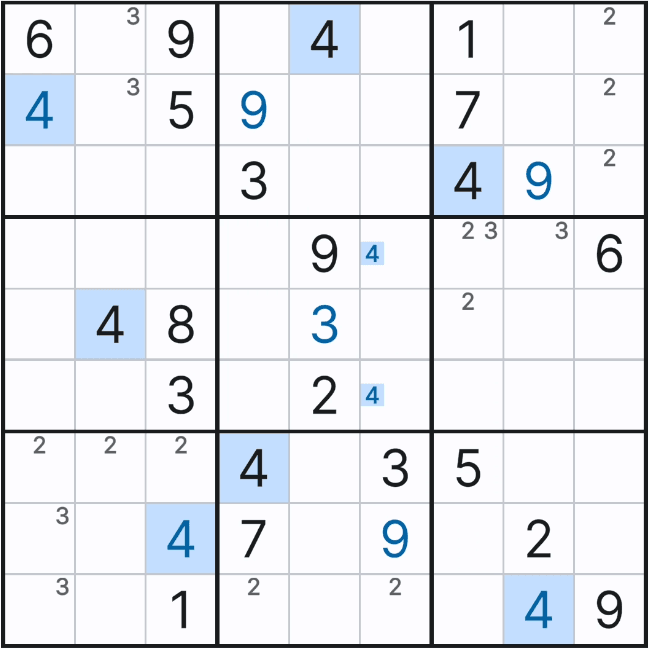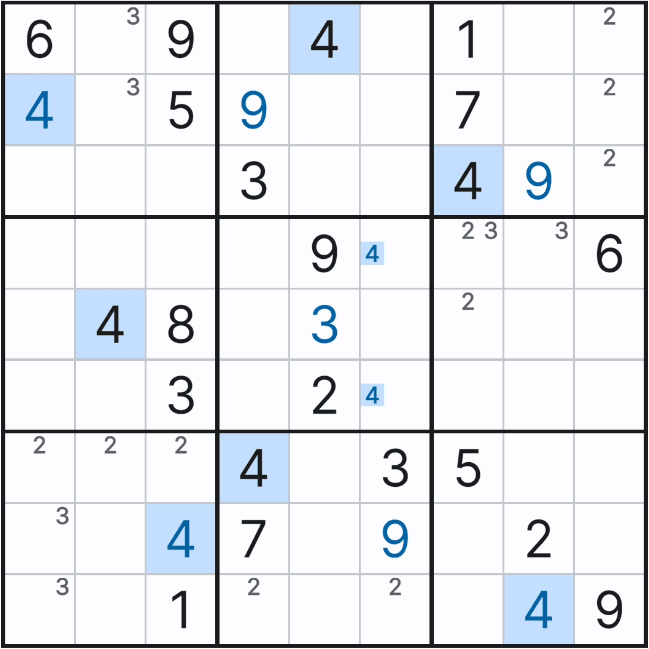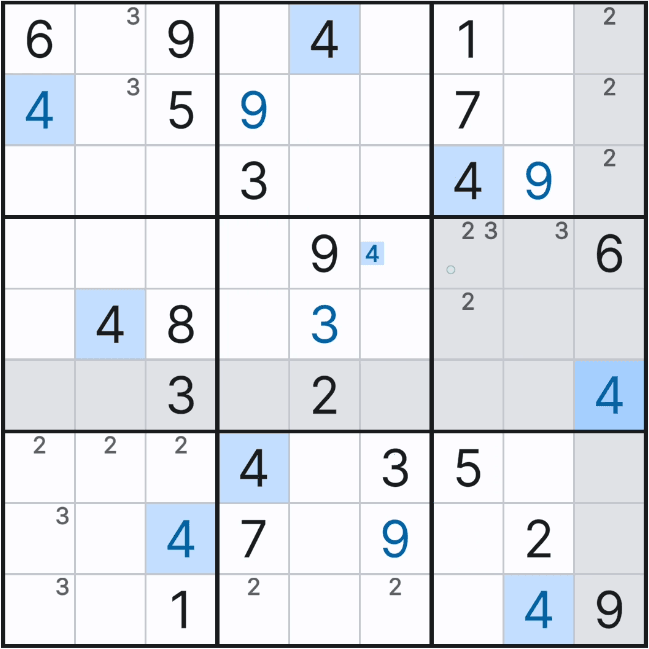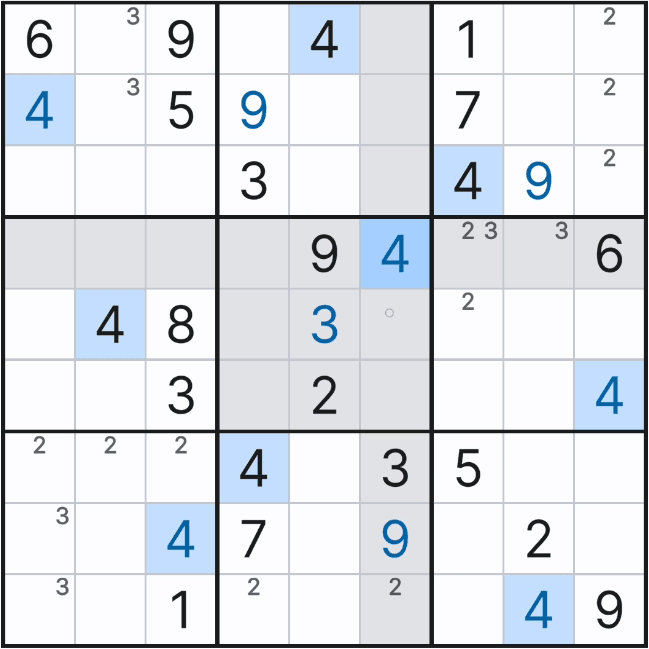
위와 같은 상황을 박스 5에 후보숫자 전체를 채웠을 때 상황과 비교해 보겠다.
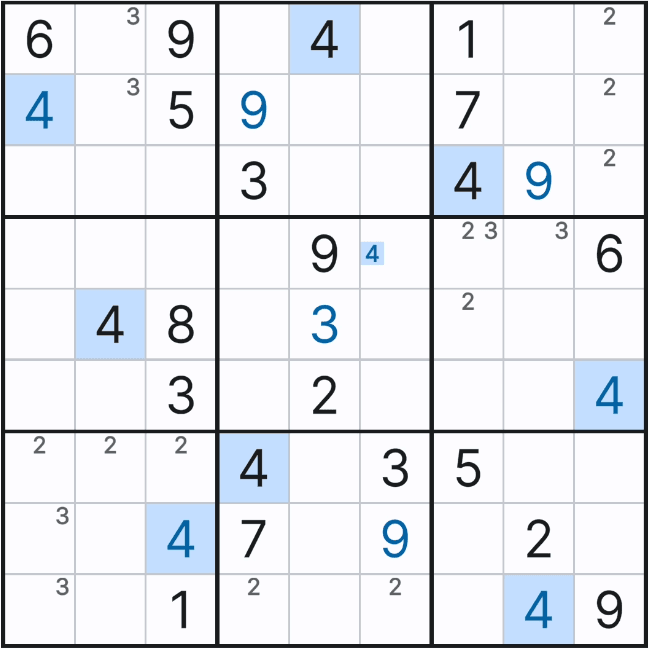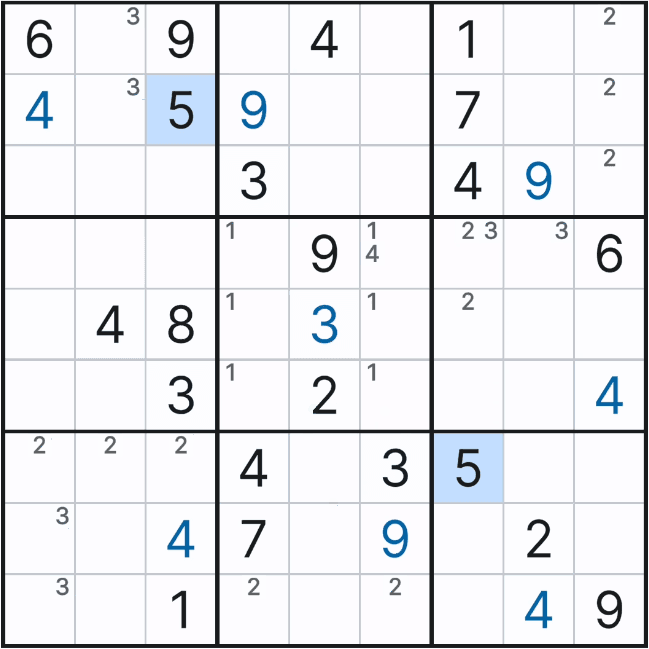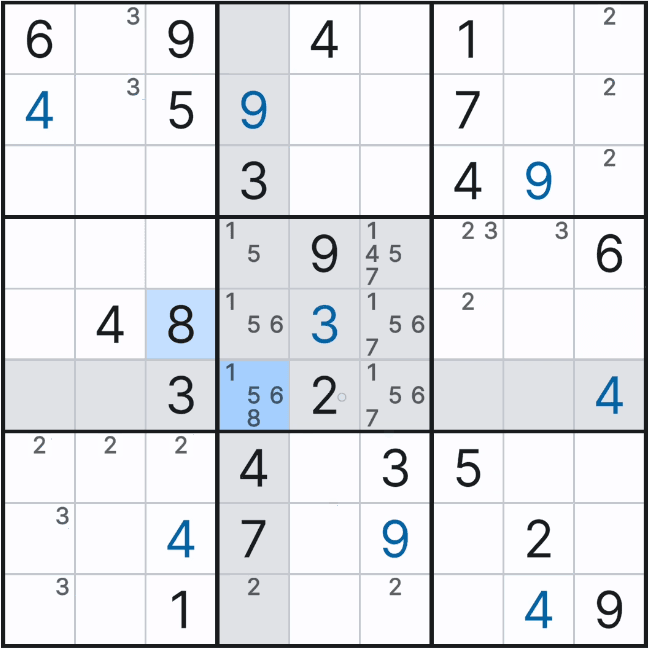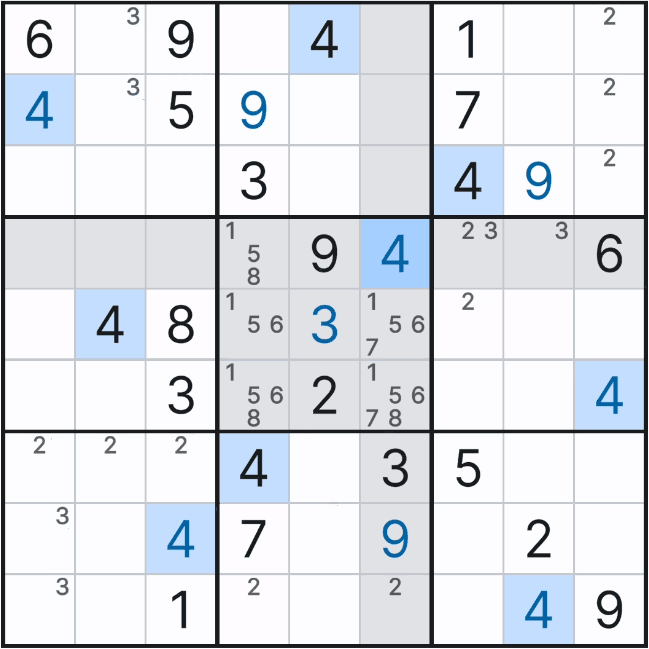
위와 같이 박스 5에 1~9까지 전체 후보숫를 채웠을 때 아래 그림과 같은 결과가 나오는데

자세히 보면 박스 5에서 (4,6)칸에만 후보숫자 4가 있음을 알 수 있다.

위와 같이 한개의 하우스 안에 후보숫자 X가 1개만 남아 있다면 여러개의 숫자 속에 숨겨져 있다고 해서 히든 싱글(Hidden Single) 또는 숨겨진 싱글이라고 부른다. 이는 우리가 알고 있는 풀하우스를 지칭하는 말이다.
숨겨진 싱글에서 다른 숫자를 제거하면 위에서 봤던 확실한 싱글의 상태가 된다.
숨겨진 싱글 (Hidden Single)
후보숫자를 채웠을 때, 한개의 하우스 (행,열,박스)에 단 하나만 존재하는 후보숫자 X를 숨겨진 싱글이라 하며 바로 확정할 수 있다.
후보숫자를 채워 가는 것과 모든 후보숫자를 채운 후 지워 가는 것을 보면 후보숫자를 채우면서 확실한 싱글을 찾는 것이 시간이 덜 걸림을 알 수 있고, 모든 후보숫자를 채운 상태에서는 정확히 확정할 숫자가 보이는 장점이 있다.
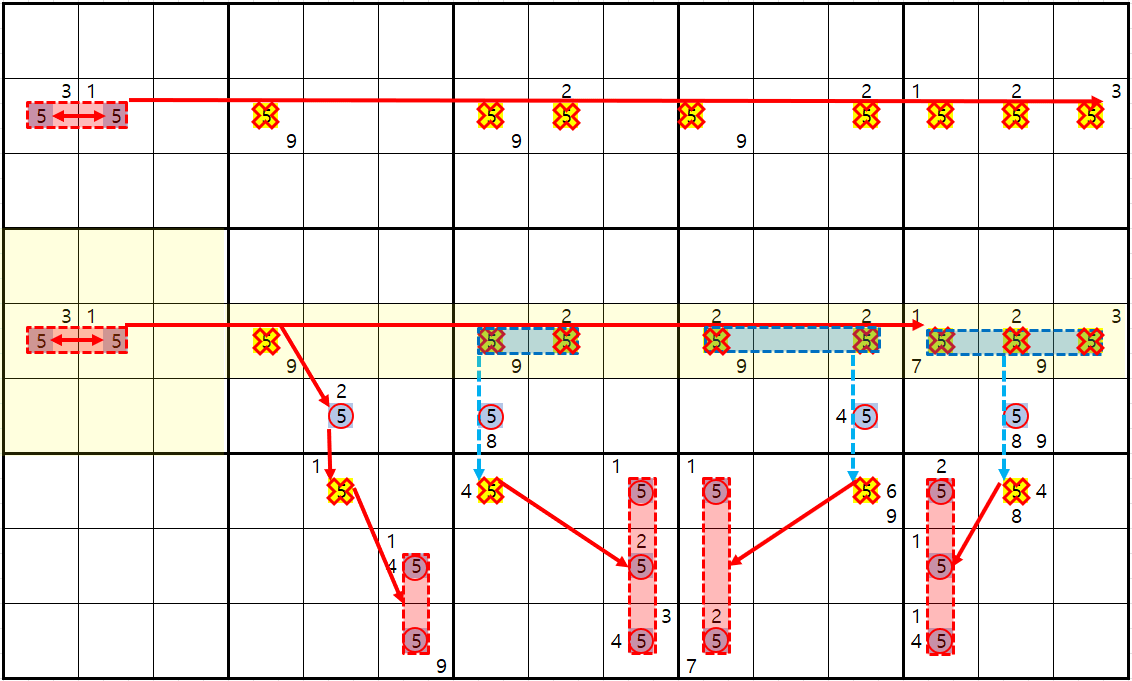
링크를 스트롱 링크와 위크 링크 2가지를 사용하면 위에서 봤던 단순한 상황에서 쓰는 방법 말고 아래와 같이 스트롱 링크(빨간선), 위크 링크(파란선)를 순차적으로 연결하는 체이닝 종류의 하나인 싱글 체인(=Single Chain, 심플컬러링) 공식에 적용할 수 있다. (나중에 알게 될테니 그렇구나 하고 보자)
다시 말하지만 스도쿠는 링크에 죽고 링크에 사는 게임이다.
이렇게 끝내면 실제 게임을 하면 단편적인 면만 봐서 스트롱 링크와 위크링크가 헷갈린다. (내가 요즘 고급 기술 넘어와서 이 간단한 링크들이 잘 보이지 않아서 고생중이다. 당연히 지금까지 쓴 개념 때문에 힘든 것은 아니다. 한정적인 예만 보고 실전을 보면 패턴이 너무 다양하다. 또한 설명이 생략된 부분도 많다.)
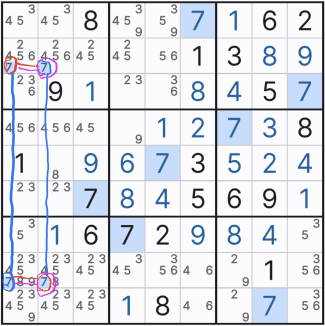
그래서 아래와 같이 스트롱 링크의 종류별로 엮은 움짤을 만들어 봤다. 모두 스트롱 링크인데 빨간선은 행에 대한, 파란색선은 열에 대한, 주황색선은 박스에 대한 스트롱 링킈의 연결이다. 아래와 같이 링크를 3개 이상 연결한 것을 체인이라고 한다.

위의 움짤만 보면 스트롱링크 찾는 것은 일도 아니다. 그저 행,열 또는 박스 안에 후보숫타 x가 2칸에만 존재하는 것을 찾으면 되기 때문이다. 단, 실전에서는 위크링크와 혼재되어 있다. 또한 위의 기본 형태 말고 변형된 형태가 되면 아래와 같아진다. 확정숫자를 찾을 때마다... 스트롱 링크가 위크링크가 되기도 하고 위크 링크가 스트롱 링크가 되는 경우가 반복될 수도 있다.
고급기술인 X 사이클이라는 스도쿠 공식을 공부하면서 힘든 것이 박스 안에서의 링크가 스트롱인지 위크인지 분간이 잘 가지 않았는데 그 이유를 알았다.

보통 위의 움짤에서 박스 1에 후보숫자 5 두 개를 연결하면 스트롱 링크고, 박스2에 후보숫자 5가 더 있다면 위크 링크로만 보게 되는데 이 것은 반만 맞다. 왜냐하면 아래와 같이
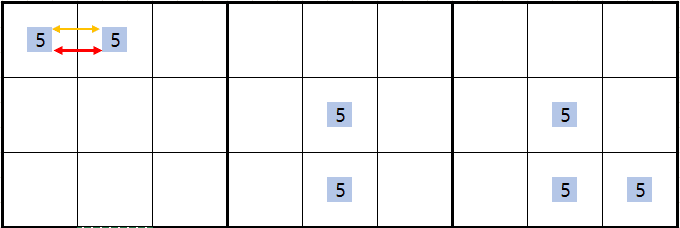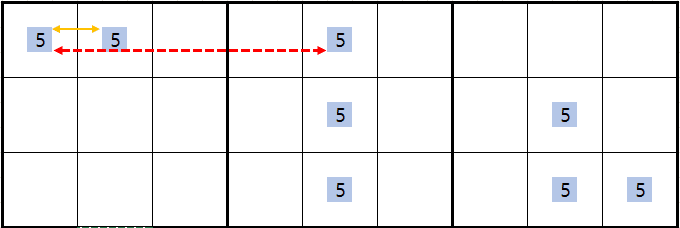
박스안에 잠긴 스트롱 링크는 이중적인 의미를 갖는다.
즉, 행에 대한 위크 링크의 성질과, 잠긴 박스에서의 스트롱 링크의 성질을 동시에 갖는다.
다시 설명하겠다. 박스안에 후보숫자 X 가 연속된 행 열에 2개만 존재 할 때는 셀에서 잠긴 후보숫자로 박스내에서는 무조건 스트롱 링크로 연결이 된다.
또 하나 어려운 개념이었던 박스내에 후보숫자 X가 교차하면서 행과 열에 대해 잠겨 있을 때는 대각선 방향으로는 위크 링크 이지만 행과 열에 대해서는 스트롱 링크가 된다.
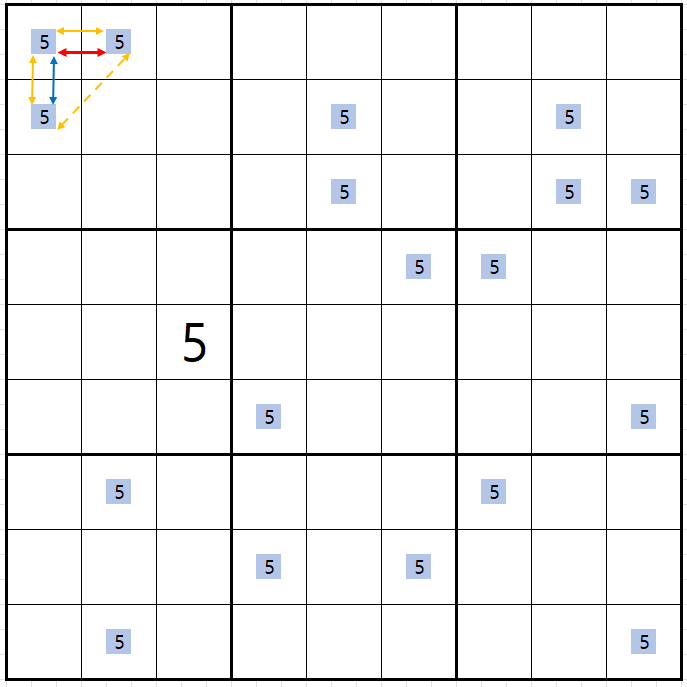
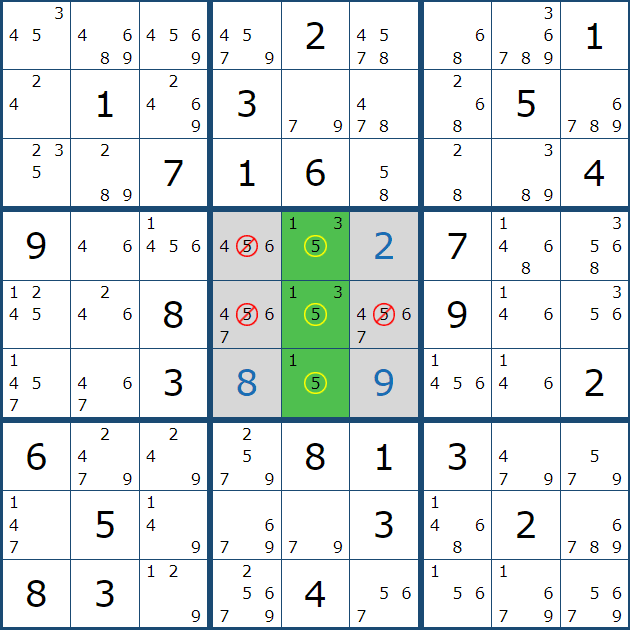
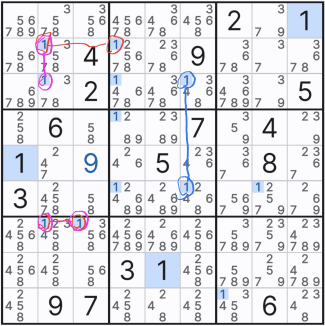
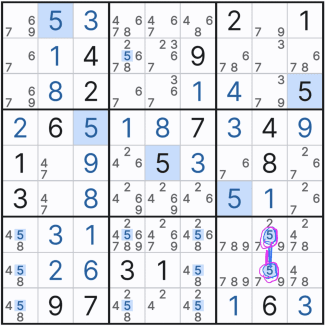
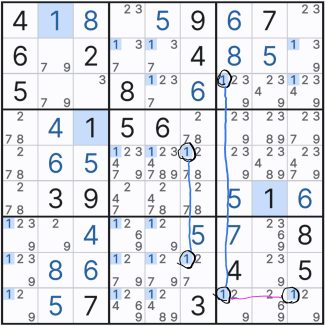
위의 그림을 살펴 보면 박스 1에 는 후보숫자 5가 3개 존재 한다.
직선 구간이라면 무조건 위크 링크가 되는 상황이지만
1행에 대해서 보면 (1,1), (1,2)칸은 잠긴 상황이기 때문에 스트롱 링크가 된다.
또한 같은 원리로 1열에 대한 방향의 후보숫자 5또한 잠긴 상황으로
(1,1), (2,1)칸은 스트롱 링크가 된다.

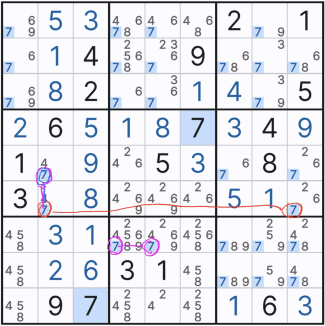
다만 (1,2) <=> (2,1) 대각선 양방향으로의 링크 관계는 조건부 관계가 되는 위크 링크이다. 물론 반대의 경우도 있다. 행열은 모두 스트롱 링크이나 박스안에서는 위크 링크가 되는 경우도 존재한다.
이런 거 복잡한데 간단히 설명하지 않고 자꾸 올리는 이유는 매우 중요해서다. 한눈에 보이는 것들은 놔두고 박스에서의 링크 관계를 유심히 보자. 스린이일 때 부터 모든 숫자를 링크의 관점으로 보길 바란다!! (나도 이 글을 쓰면서 스트롱, 위크 링크가 좀 명쾌해 졌다.)
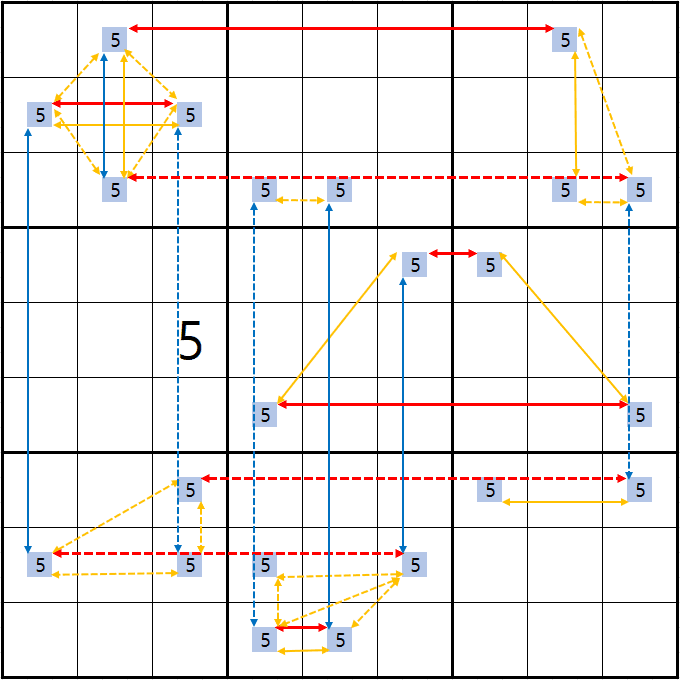
마지막으로 언제나 강력한 링크가 되는 경우가 또 하나가 있다. 위의 그림에서는 숫자 5에 대해서만 썼는데 아래와 같이 다른 숫자와 연결될 때, '이중 위치'링크 XY- XY끼리의 링크는 같은 하우스에 3개 이상의 숫자가 있어도 아래 그림과 같이 언제나 스트롱 링크가 된다.
알고 있다. 위의 설명만으로는 감이 안 온다는 것을 실전에서 스트롱 링크만 표기한 그림 49개를 올린다(아래 '더 보기'를 눌러 보자. 그림 클린 또는 터치후 스크롤해서 보는 것을 추천한다.) 부디 마지막 세 개 그림의 의미를 깨닫기를 바란다. 그럼 더욱 더 차원이 높은 스도쿠 세계의 지름길을 가는 것과 같다고 분명히 말할 수 있다.
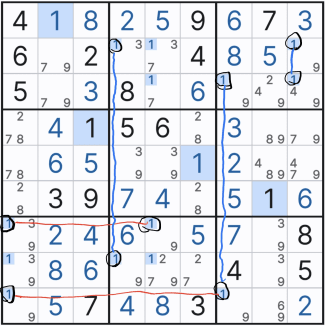
아래 예제는 스트롱 선이 그어지지 않은 스트롱 링크 외에 선이 없는 박스내에서의 위크 링크에 집중해서 보기를 권한다. 빨간선 > 수평, 파란선 > 수직 > 핑크선 > 박스내 스트롱 링크 표시
Andoku 스도쿠 3 - 강력 스도쿠 추천 앱
스도쿠에 빠져든지 2달이 막 지나는 지금 현재까지 10가지 정도의 앱을 광고 보면서 써보고 2개의 앱을 유료결제로 사용하다가 전문가 난이도인데 뭔가 맥없이 풀리는 것 때문에 조금 스도쿠의
inoks.tistory.com