노노그램 이중가정법을 써야할까 말아야 할까 계산해보자

 10x10, 15x15 그리드를 갖는 노노그램은 비교적 이중가정법을 쓰는 상황이 직관적으로 잘 보이는 경우가 만지만 난이도가 높아질 수록 아래와 같이 총 40개의 행과 열 중에 단, 6개의 줄만 이중가정법이 적용되는 상황이 있다. 

 

 

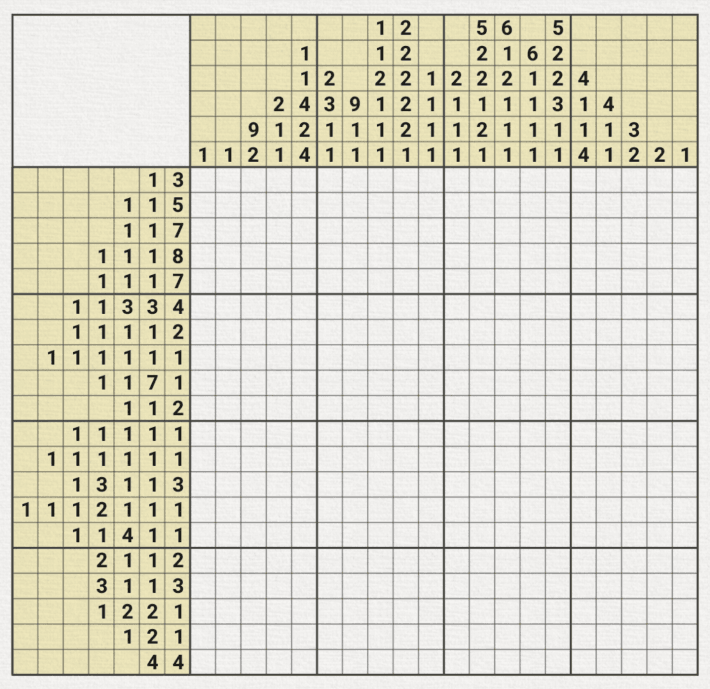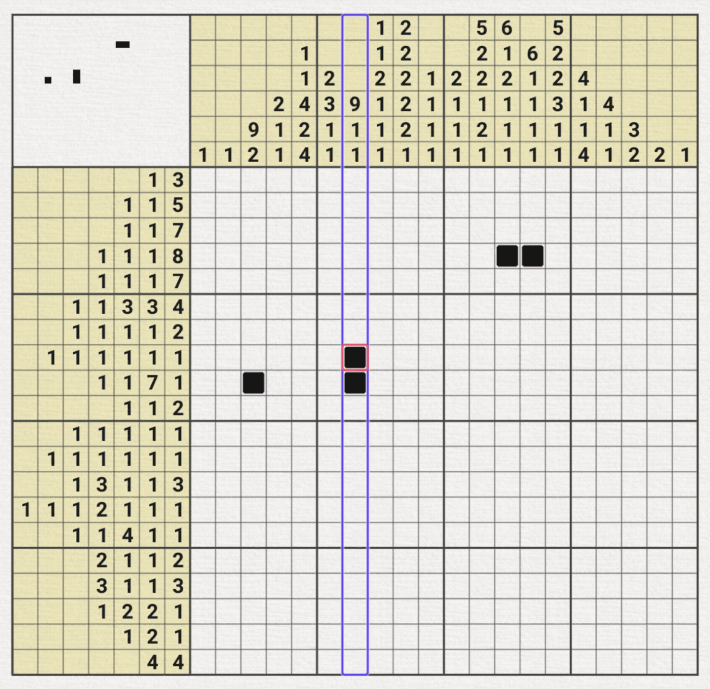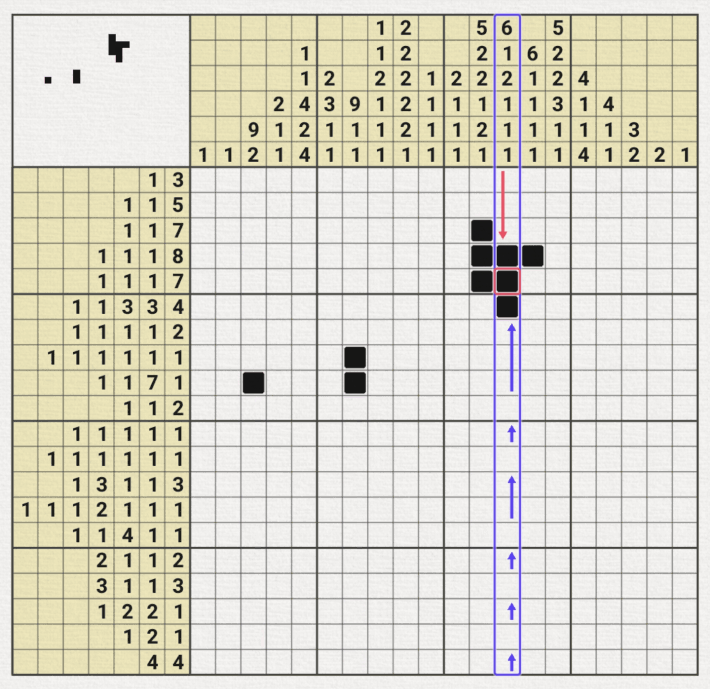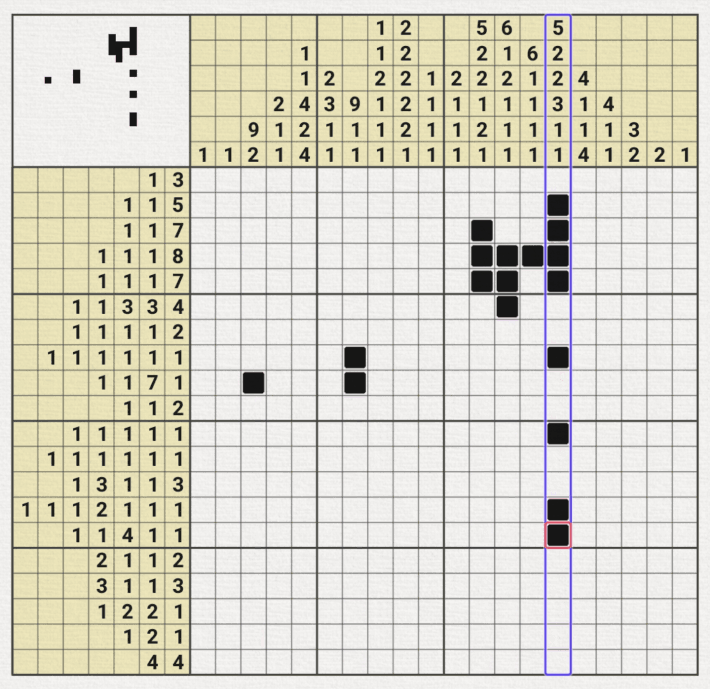
 물론 직관적으로 보면서 큰 숫자 위주로 초반 공략을 하면 되지만, 어려운 판일 수록 미묘하게 1 또는 2가 많이 들어가면서 딱 1칸만 이중가정법이 적용되는 줄이 있는데, 놓치게 되면 중반이 어려워 질 수 있기 때문에 

 

 모든 줄에 대해 보조선을 긋지 않아도 어떤 상황에서 이중가정법이 적용되고 않되는지 이해를 하면 더욱 더 잘 찾을 수 있을거라고 봅다. 설명의 용이함을 위해서 10x10 그리드를 준비했다.

 

 준비.. 뭐 아래와 같은 큰 숫자는 잘 보이기 때문에 이중가정법 적용을 잘 할 것이다. (암산으로도 가능하다~)

 

1. 2칸인 경우에서 계산

    아래 움짤에서 5행의 1/4를 보자.

 

 

 5행을 보면 1/4가 있는데

 

 다 더하면 6이 된다. 

 

 좌측에서부터 6칸의 보조선을 긋더라도

 우측에서 시작하는 숫자 4개의 칸의 합이

 6+4=10이므로 겹치는 칸이 없다. 

 

 이걸 다시 산수로 계산하면 

 1+4+1(빈칸)=6개의 칸을 

 

 전체칸수 10칸에서 빼주면 4칸이 남는데.

 

 1/4중에서 최우측에서 시작하는 4로 빼주면

 

 0이 되기 때문에 겹치는 칸이 없으므로 다음 줄을 조사하면 되겠다.  

 

 큰 의미는 없을 줄로 알지만 1/3과 1/2의 숫자를 갖는 행도 살펴 보자.

 

 여기까지도 준비운동이라고 보고 이제 아래와 같이 3개의 숫자가 있을 경우를 살펴보자!!

 

 

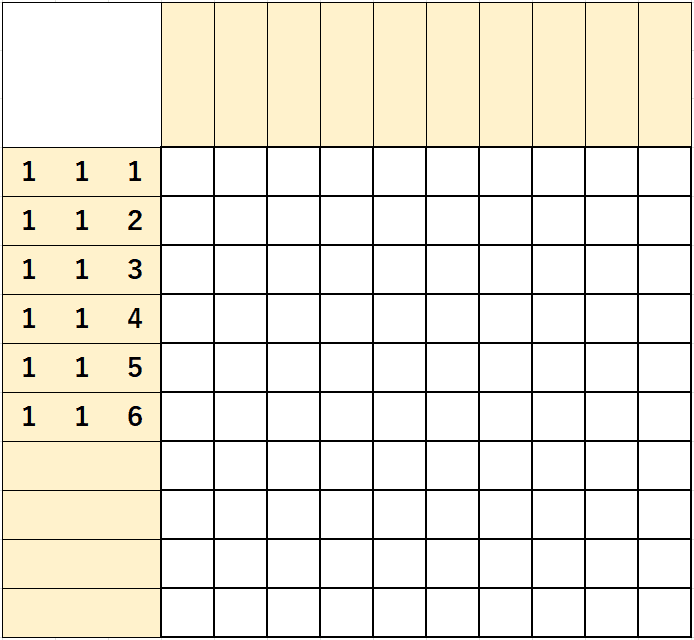
2. 세개의 숫자중 우측(or 좌측) 의 숫자가 큰 경우... 

 

 다른 숫자들의 크기에 따라 경우가 달라지지만 대부분은 큰숫자 뒤의 숫자는 교집합이 적은 경우가 많다. 

 

 

 숫자가 2개일 때랑 같다. 

 

 위의 경우를 보면 1/1/1이나 1/1/2는 설명할 이유가 없을 정도로 여러분에게 잘 보일 것이므로 3행부터 설명하면

 

 3행의 1/1/3 은 더하면 5가 되고 빈칸은 필히 2개가 들어가야 하므로

 1+1+3+2=7이 된다. 

 

 전체 칸 10칸에서 위의 7칸을 빼면

 10-7=3칸 이 남게 되는데

 

 최우측에서 시작하는 3에서 빼주면 3-3=0이 되어 겹치는 칸이 없으므로 다음 칸으로 넘어가야 한다. 

 다른 표현으로 보자면

 

 좌측에서 시작하는 최대 칸수는 7칸

 우측에서 시작하는 큰 숫자의 최대칸수는 3이므로 

 3-(10-7)=0이므로 겹치는 칸이 없다. 

 

 4행의 경우는 1/1/4 로 빈칸 2칸을 포함하면 

 1+1+4+2=8 칸이 되므로

 

 전체칸수 10칸에서 8칸을 빼면 2가 되며

 10-8=2

 

  최우측에서 시작하는 4에서 빼주면

  4-2=2칸이 되므로 

 이중가정법으로 교집합을 찾으면 되겠다. 

 

다른 표현으로 하자면

 

4-(10-8)=2가 되므로 이중 가정법으로 2칸이 겹치게 되는 것을 찾을 수 있다. 

 

5행의 경우는

좌측에서 보면 1+1+5+2=9이므로

 

5-(10-9)=4 칸이 겹치게 된다. 

 

6행의 경우는 

좌측에서 보면 1+1+6+2=10이므로 

전체 칸수가 채워지기 때문에 바로 모든 칸을 순서대로 마킹하면 되겠다.

 

2. 숫자가 3개 중 중앙의 숫자가 큰 경우

 

 

 숫자 3개 중에서 중간의 숫자가 큰 경우에는 가장자리의 숫자가 적은 것을 제외한 후에 계산하면 되겠다.

 

5행은 1+6+1+2=10으로 당연히 가득차는 칸이 되므로 순서대로 마킹하면 되겠다. 

 

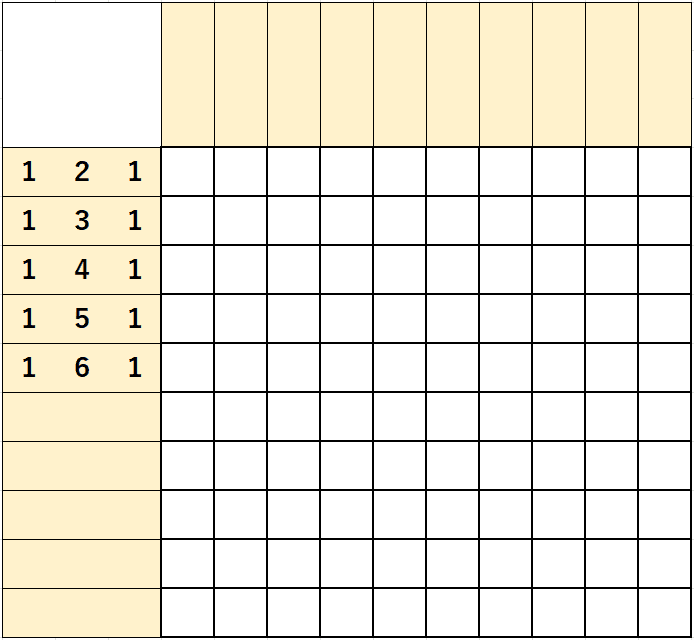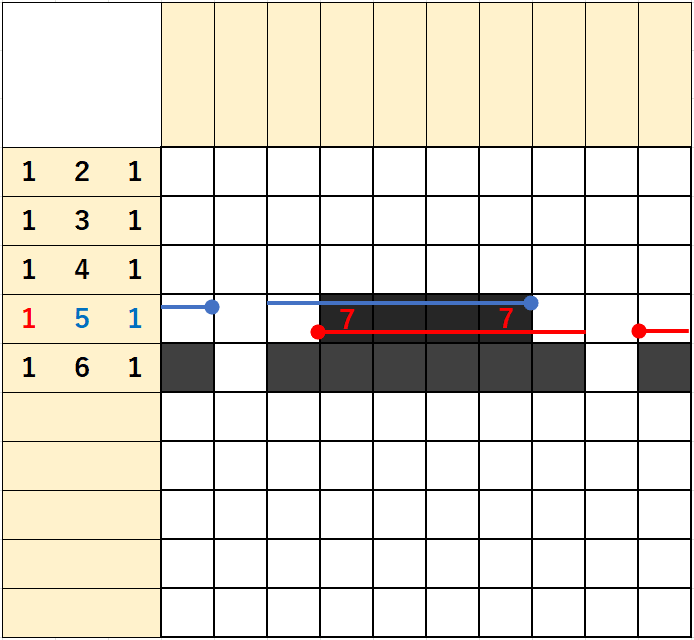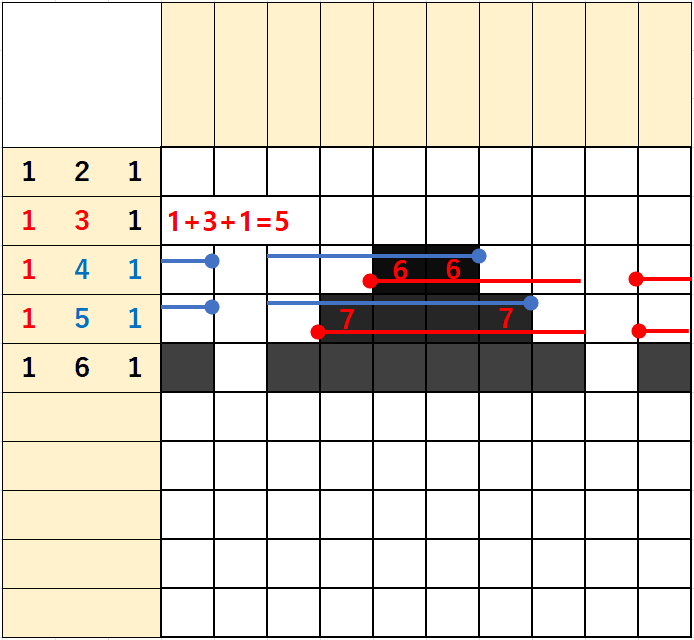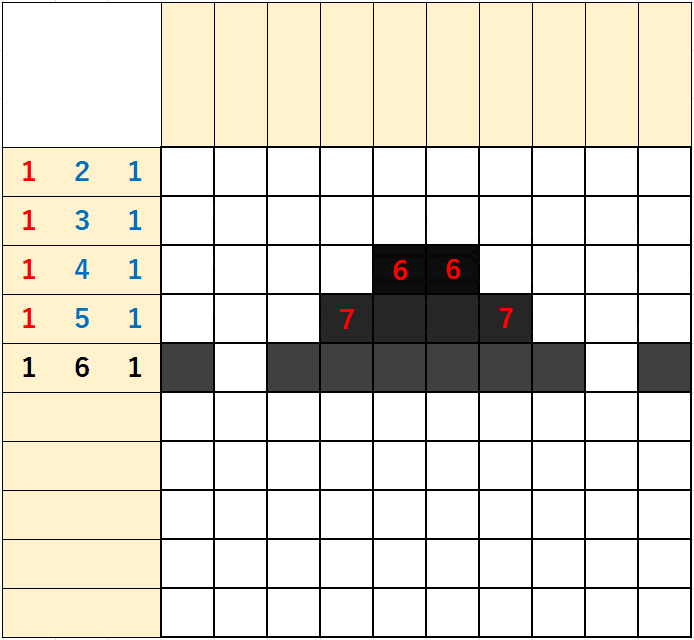
4행은 1/5/1이 있는데

1)좌측에서 출발하는 1/5에 빈칸 1을 더하면 1+5+1=7이 되고

2)우측에서 출발하는 1/5에 빈칸 1을 더하면 1+5+1=7이 되어

 

단일 숫자처럼 좌측에서부터 7번째칸 우측에서부터 7번째칸을 잇는 4개의 칸이 겹치게 된다. 

 

위에서 살펴본대로 산수로 표현해보면

 

(1+5+1)-(10-(1+5+1)) = 7-(10-7) = 4칸이 겹침

 

3행은 숫자가 1/4/1이 있는데

1)좌측에서 출발하는 1/4에 빈칸 1을 더하면 1+4+1=6이 되고

2)우측에서 출발하는 1/4에 빈칸 1을 더하면 1+4+1=6이 되어

 

단일 숫자처럼 좌측에서부터 6번째칸 우측에서부터 6번째칸을 잇는 2개의 칸이 겹치게 된다. 

 

위에서 살펴본대로 산수로 표현해보면

 

(1+4+1)-(10-(1+4+1)) = 6-(10-6) = 2칸이 겹침

 

1행과 2행은 여러분도 잘 알겠지만~

 

2행은 숫자가 1/3/1이 있는데

1)좌측에서 출발하는 1/3에 빈칸 1을 더하면 1+3+1=5가 되고

2)우측에서 출발하는 1/3에 빈칸 1을 더하면 1+3+1=5가 되어

 

단일 숫자처럼 좌측에서부터 5번째칸 우측에서부터 5번째칸을 잇는 칸이 없는 것을 알 수 있다.

 

위에서 살펴본대로 산수로 표현해보면

 

(1+3+1)-(10-(1+3+1)) = 5-(10-5) = 0이 되어 겹치는 칸이 없음

 

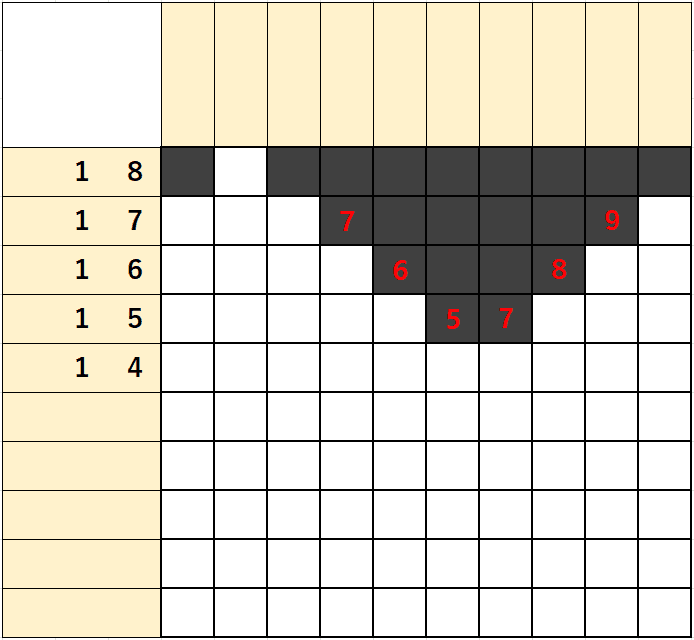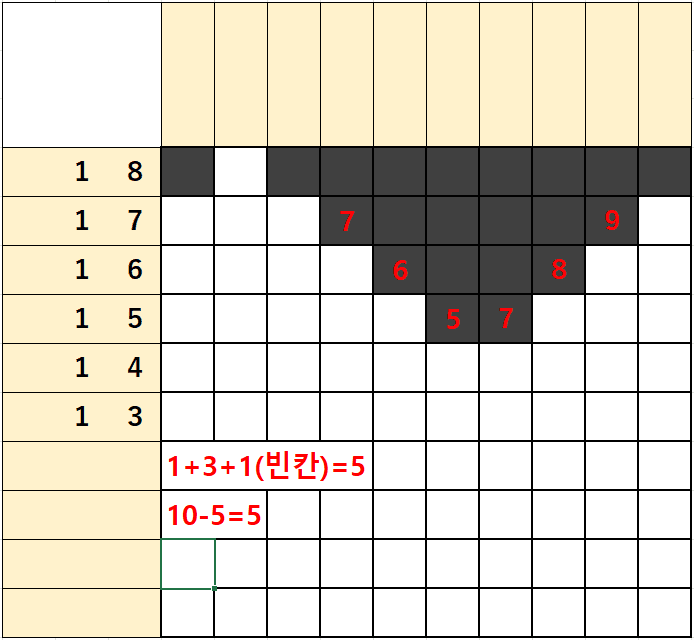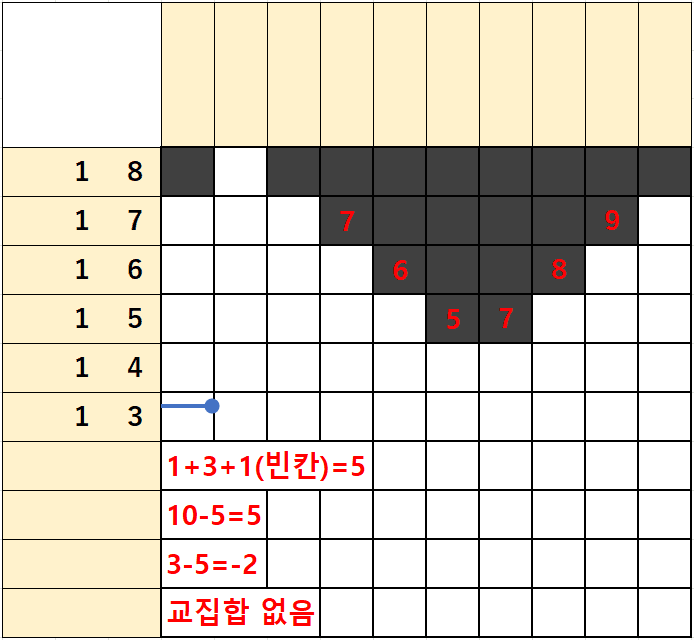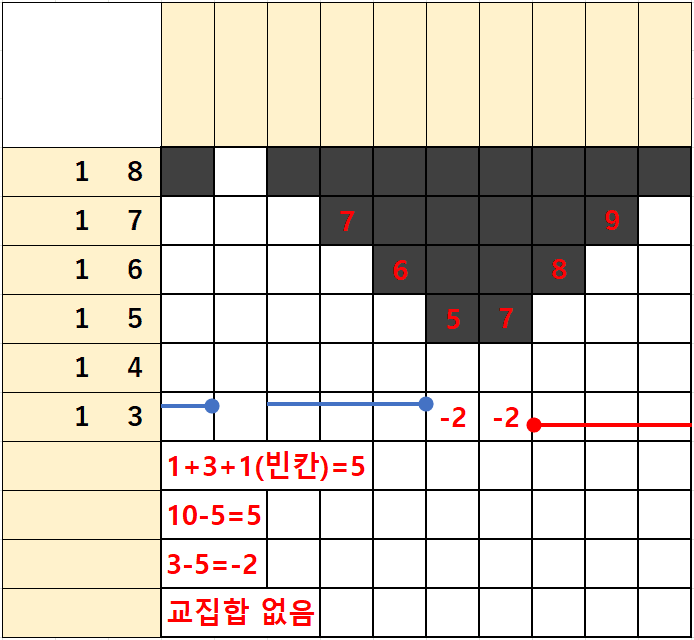
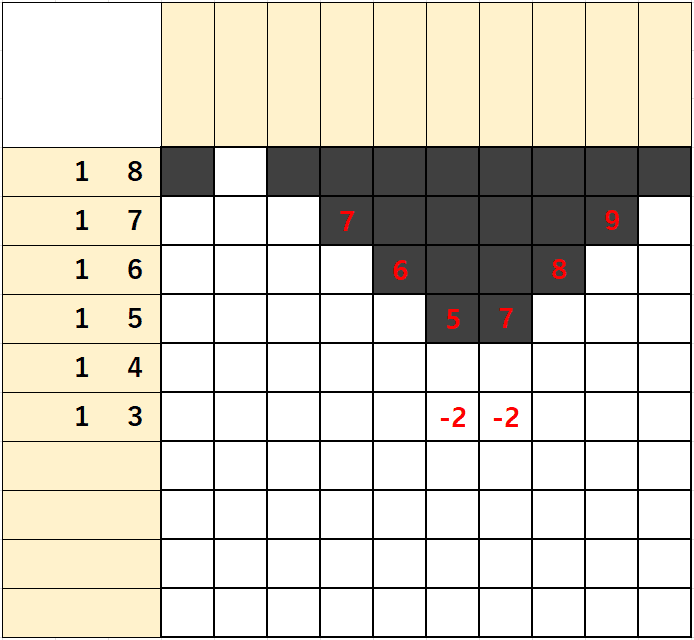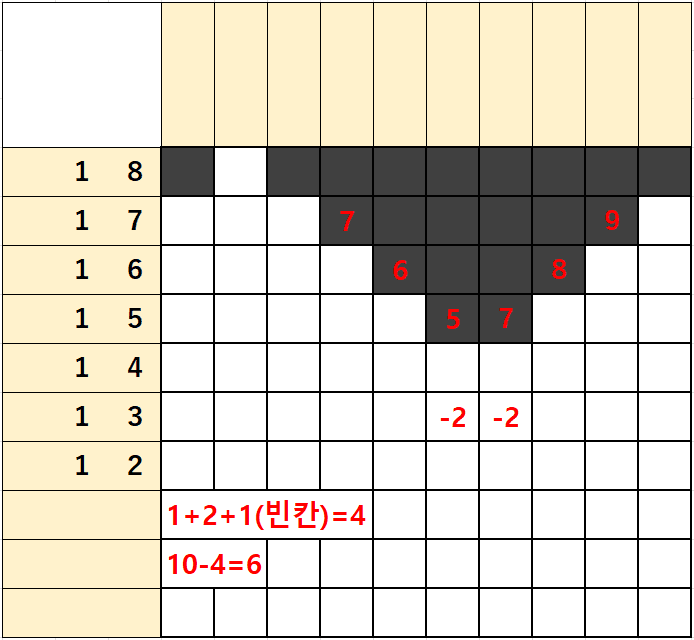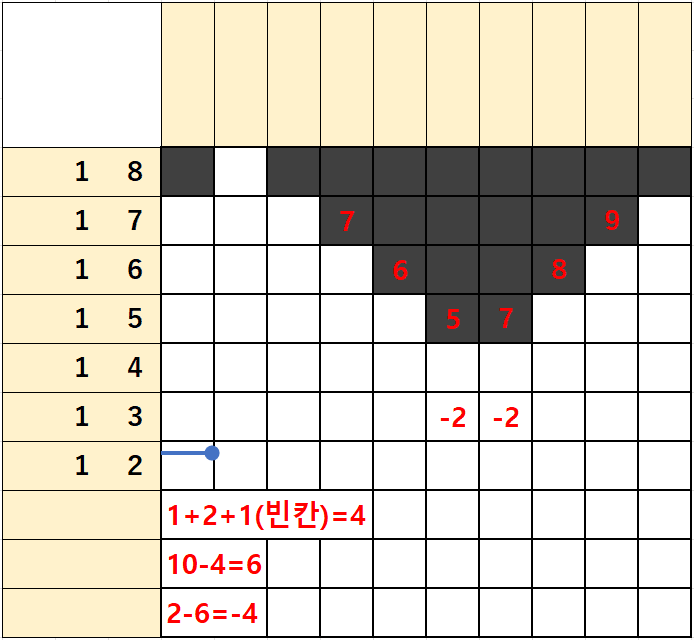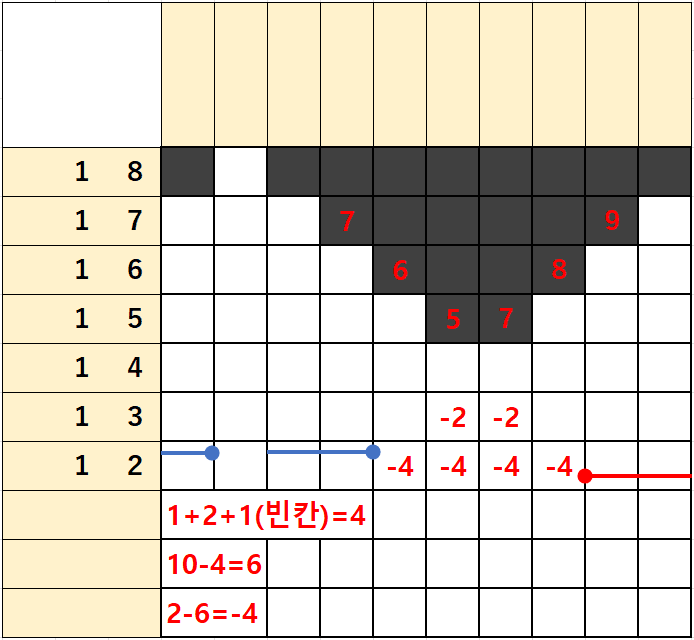
1행은 숫자가 1/2/1이 있는데

1)좌측에서 출발하는 1/2에 빈칸 1을 더하면 1+2+1=4가 되고

2)우측에서 출발하는 1/2에 빈칸 1을 더하면 1+2+1=4가 되어

 

단일 숫자처럼 좌측에서부터 4번째칸 우측에서부터 4번째칸을 잇는 칸이 없고 2칸이나 떨어진 것을 알 수 있다.

 

위에서 살펴본대로 산수로 표현해보면

 

(1+2+1)-(10-(1+2+1)) = 4-(10-4) = -2이 되어 겹치는 칸이 없이 2칸이 떨어지는 것을 알 수 있다.

 

---------------------------------------------

 

음 여기까지 읽었으면 이게 뭐야? 싶을 수도 있는데. 분명히 노노그램 퍼즐에서 난이도가 높아질 수록 도움이 될 거라 믿고 2번만 더 보자...

 

 숫자 조합이야 무궁무진해서 간단하게만 적었지만 2/3/3, 1/1/1/2/1, 1/1/2/1/2 등의 숫자가 나오면 위에서 본 개념이 더욱 더 도움이 되는 것을 알 수 있게 될 것이다~

 

 

 

음. 몇일전에 컬러 노노그램을 영접했는데...

멈출 수가 없드아!!

 

 

 

 

 

움짤로 익히는 컬러 노노그램만의 규칙

움짤로 익히는 컬러 노노그램만의 규칙