노노그램 막혔을 때, 요긴히 써 먹는 '귀류법'

숫자를 따라 노노그램을 풀다 보면 후반부에 막혀서 포기하는 경우가 가끔 있을 것이다.

숫자로만 노노그램이 풀리지 않을 때는

  참이라는 가정하에 모순을 찾아내어 참이라고 가정한 부분에 X표를 칠하며 답을 찾는 방식을 귀류법 풀이라고 한다.

위와 같은 판이 있을 때, 당연히 2행 4행, 2열 4열의

2/2가 핵심이지만 막힌 상황이라고 가정하고 1행의 3을 가지고 귀류법에 대해 알아보겠다.

A. 1행의 1~3열이 해라고 가정할 때

 

 

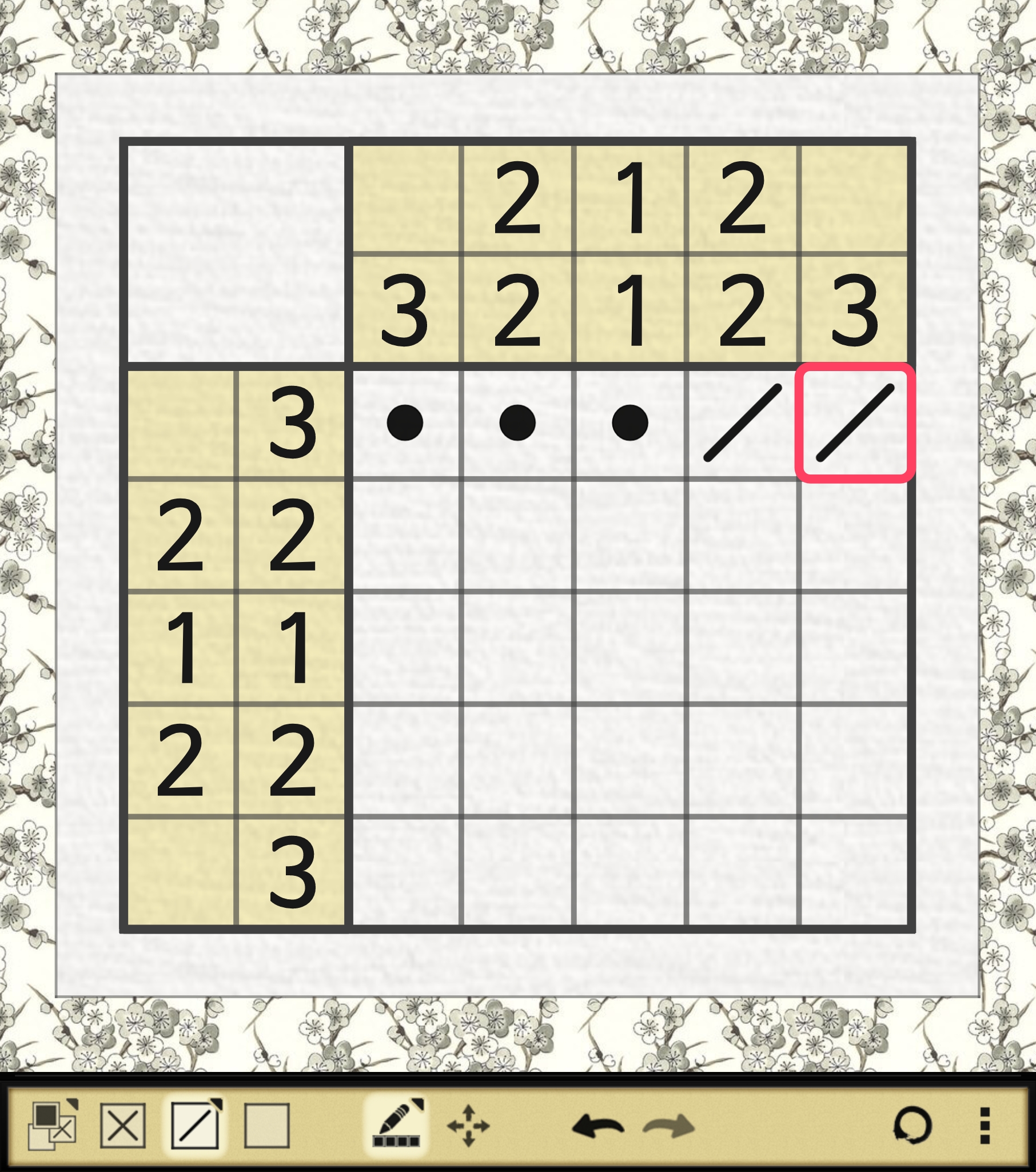
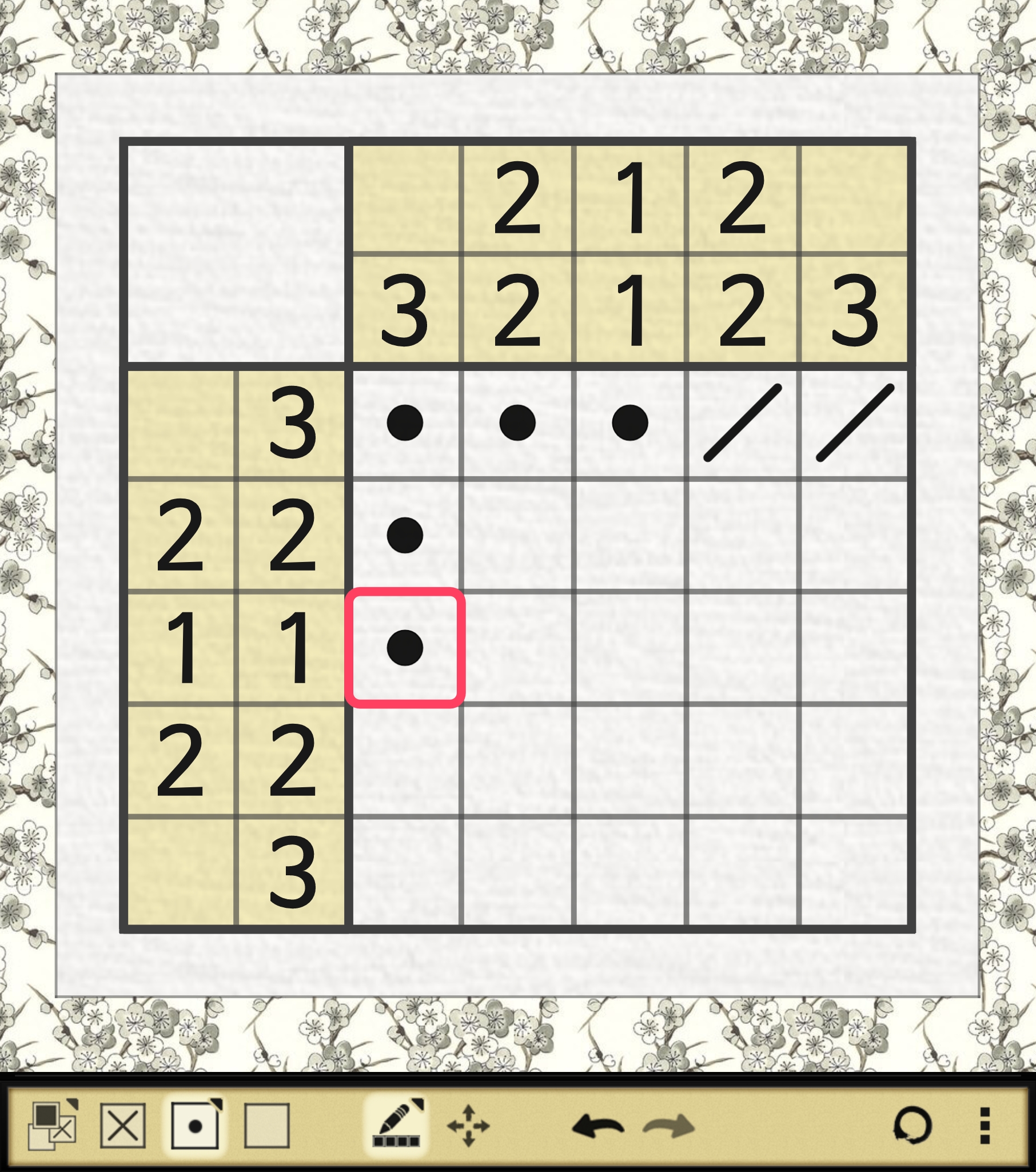
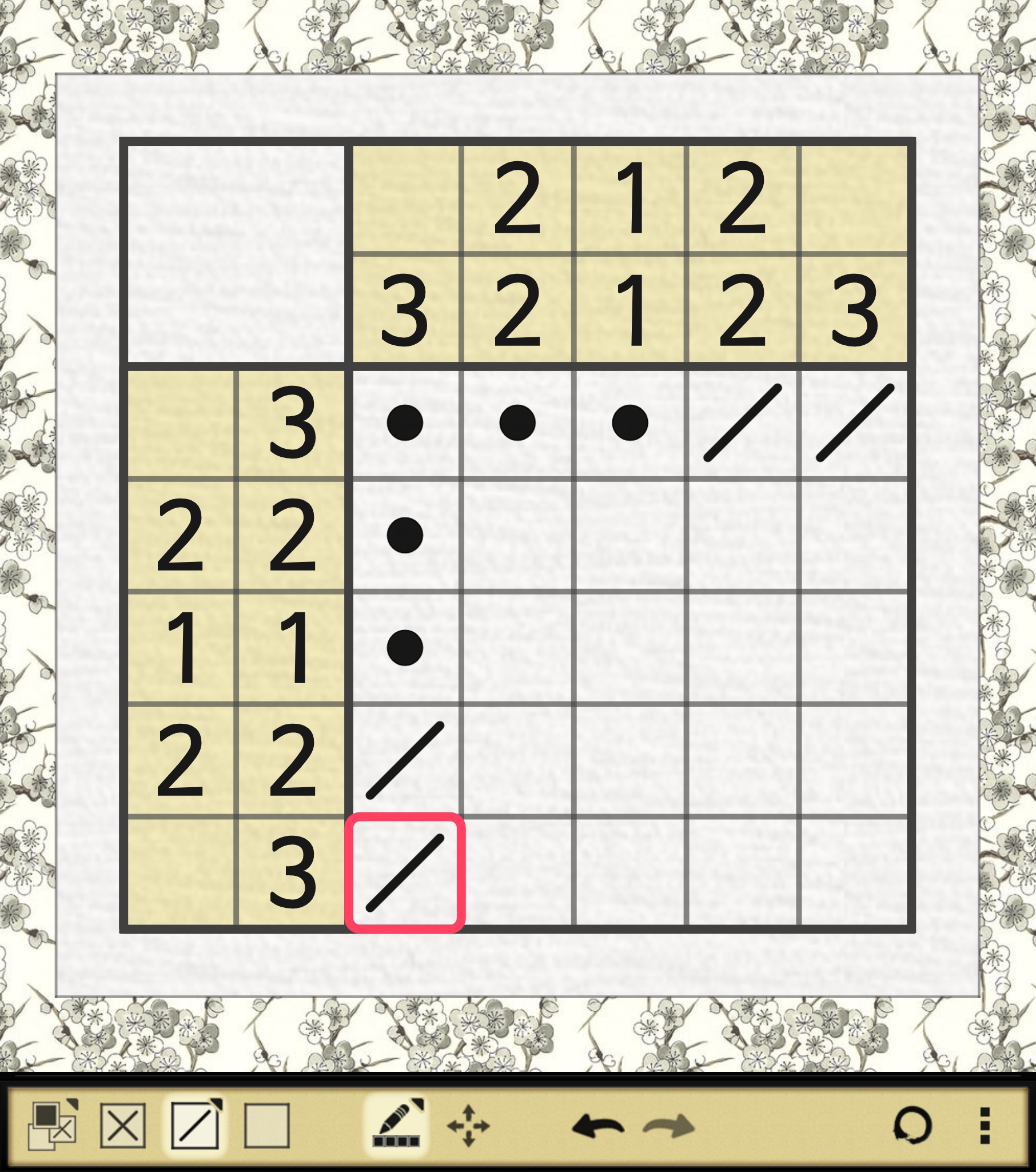
가 되는데 아래 짤을 보면

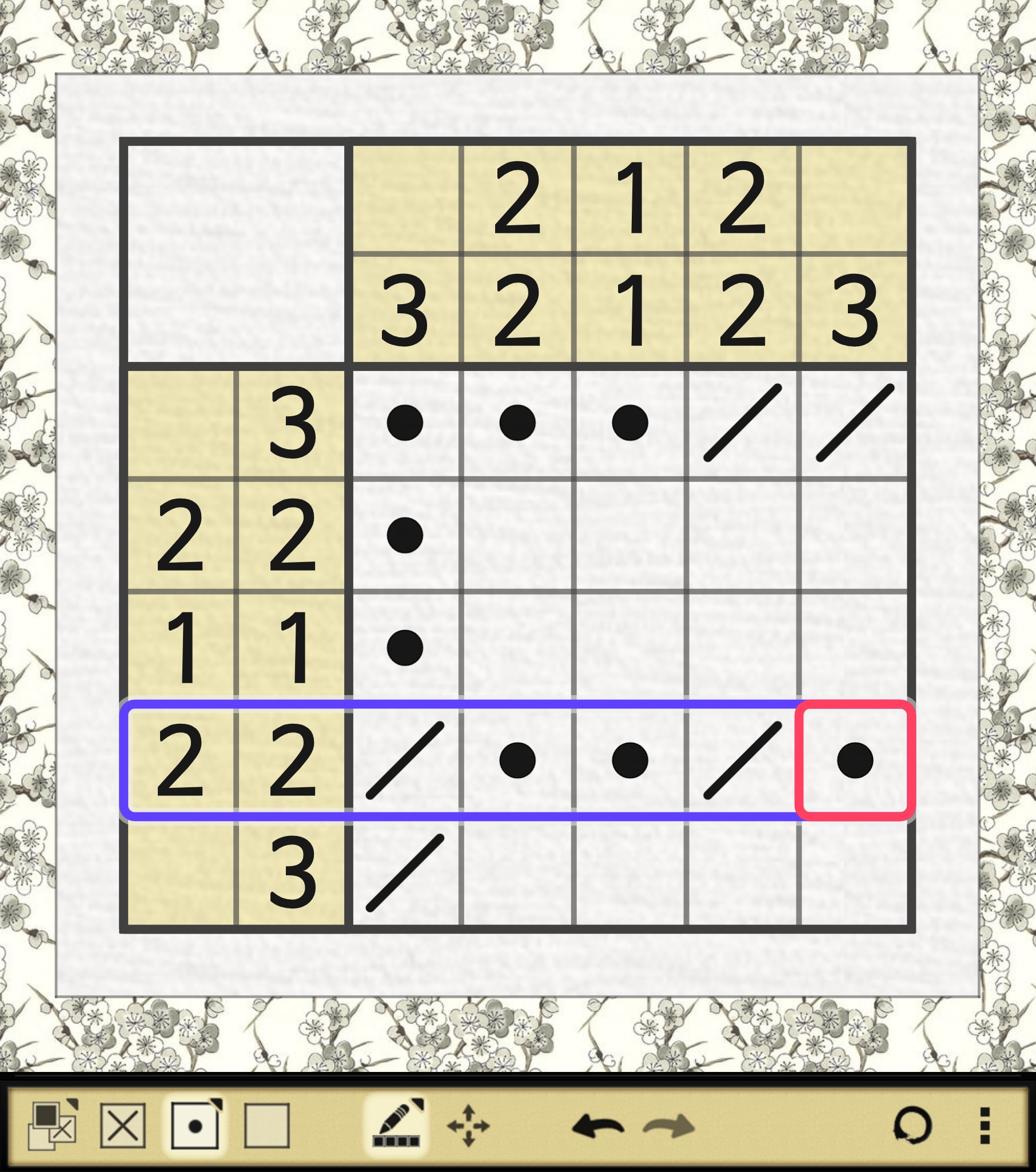
4행의 2/2가 모순이 되는 것을 알 수 있으므로

1행 1열은 ㅁ가 될 수 없고 X 가 되어야 한다.



B. 1행의 3~5열이 해라고 가정할 때

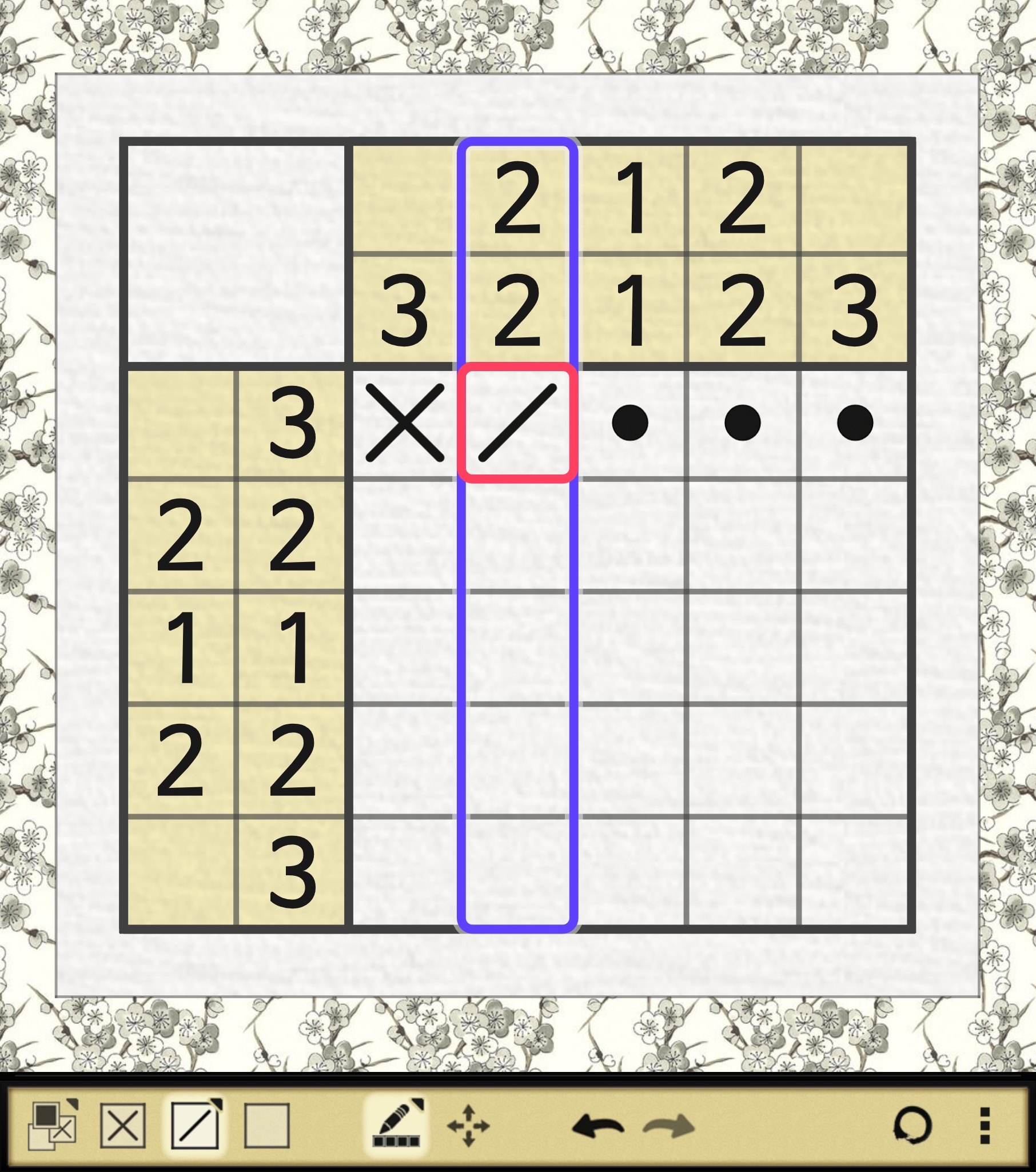
위의 짤과 같이 2열에 다음과 같은 모순이 발생한다.

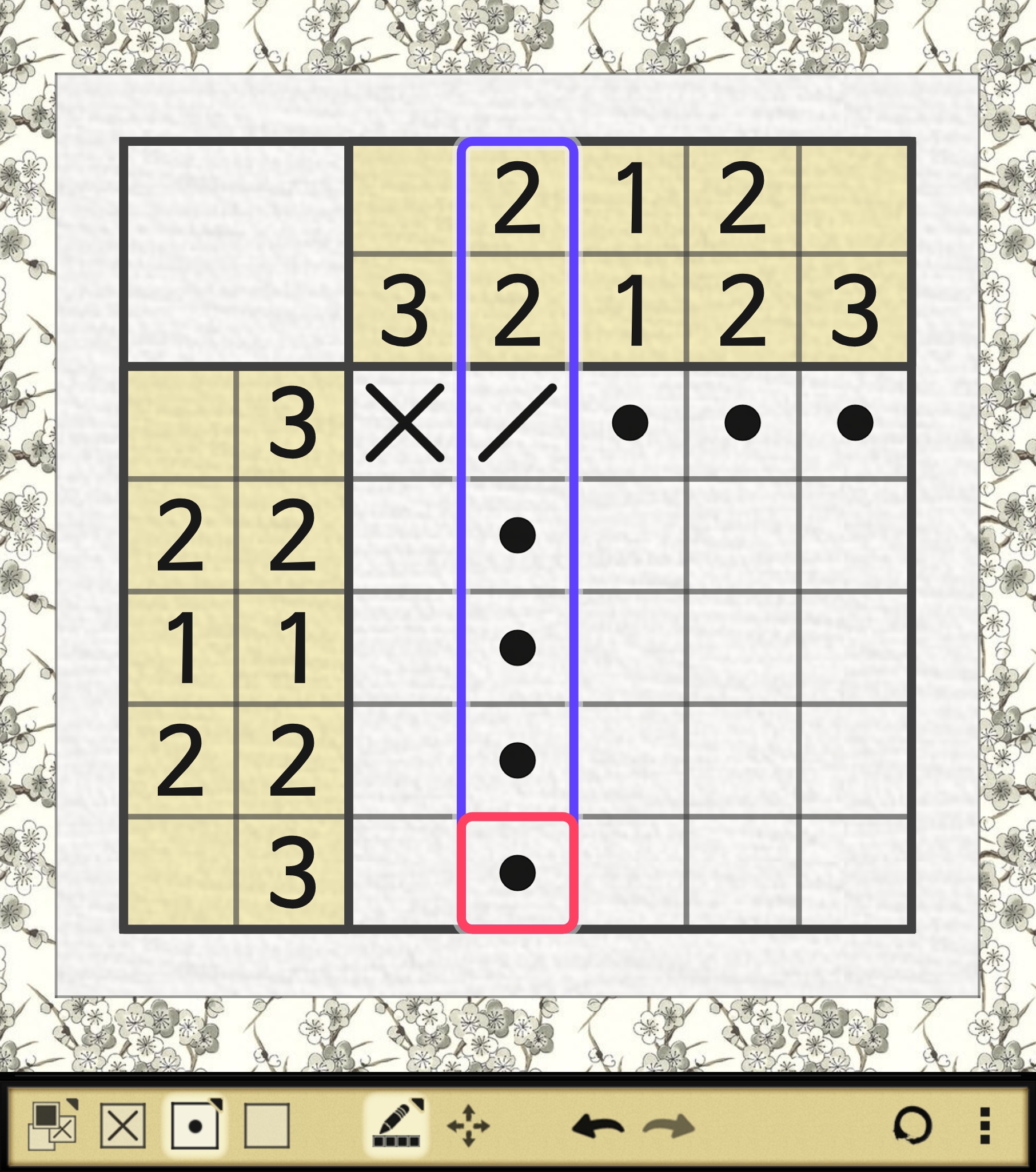
2열에 모순이 발생하므로 1행 5열은 ㅁ가 될 수 없고 아래와 같이

거짓인 X표를 하면 된다.

위에서 본 A와 B의 모순의 결과로
1행 2~4열 3칸이 해가 되는 것을 알 수 있다.

5x5 판이라 풀이 과정이 필요 없겠지만

위에서 귀류법으로 제거하고 남은 방식의 풀이를

스맛폰 기준 한 화면 밑에 그림파일로 올리도록 하겠다.

모쪼록 더 즐거운 노노그램 하기를 기원한다.


https://youtube.com/shorts/7FR6aqhJDtI?si=17zyCXILSe03MwAy

 

위의 유튭 링크는 10*10 판에서 실제로 막혔을 때를 가정해서 귀류법으로 푸는 (허접하지만 이해도 높혀주는) 영상을 만들어 봤다. 꼭 보길 권한다.

 

 

 

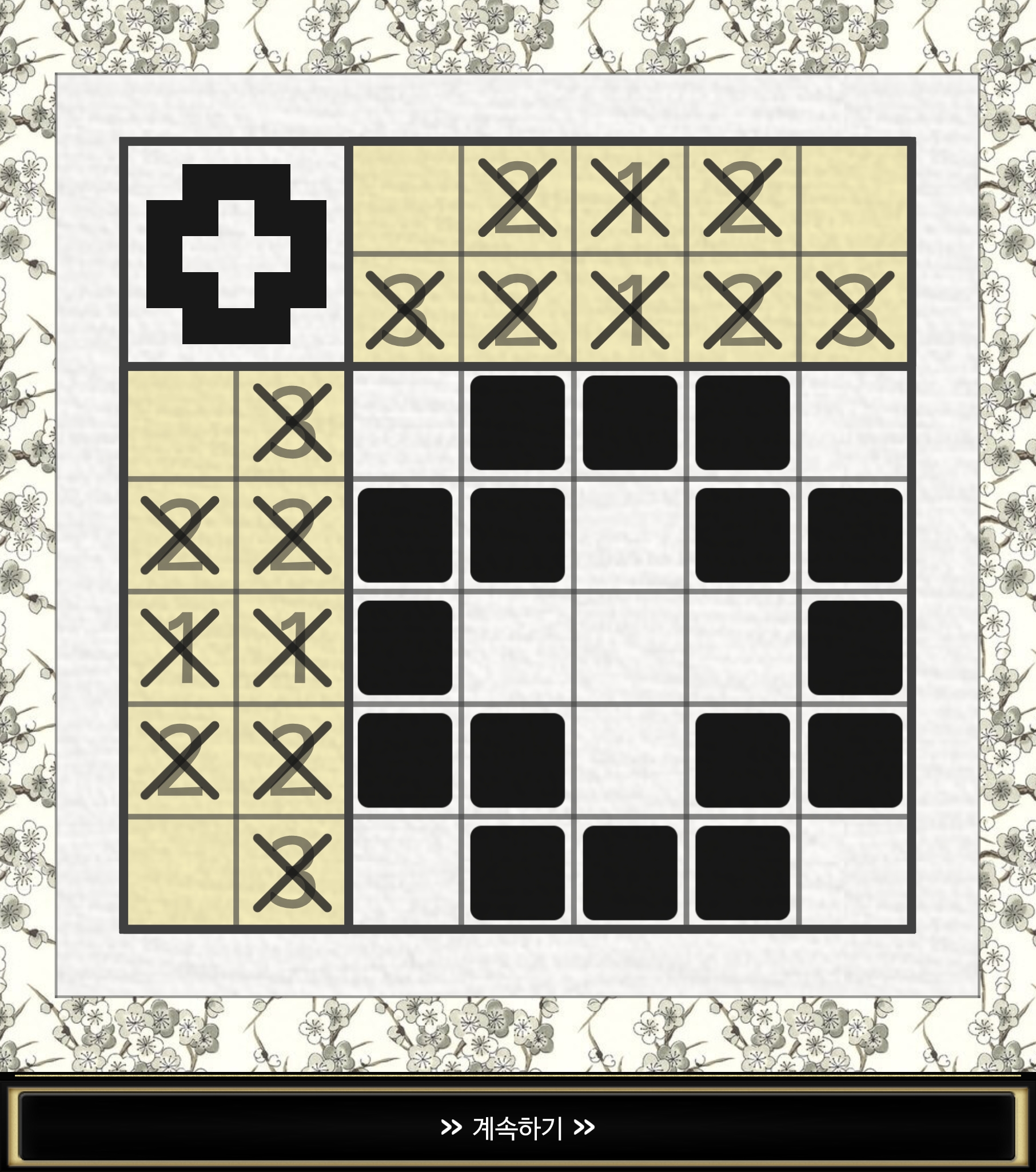
5월 19일 추가

 

10x10 판 우습게 봤다가 귀류법을 2번이나 실제로 쓴 게임이 있었다. 

 

1번째는 오류를 찾아서 고쳤고 

 

 

 

 

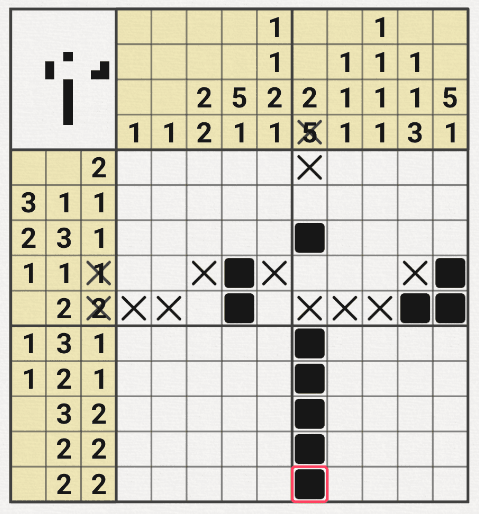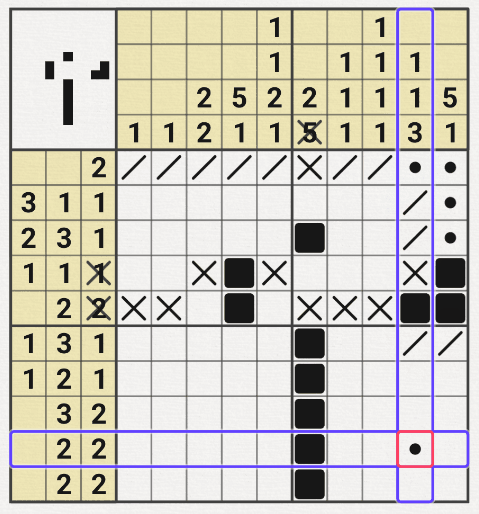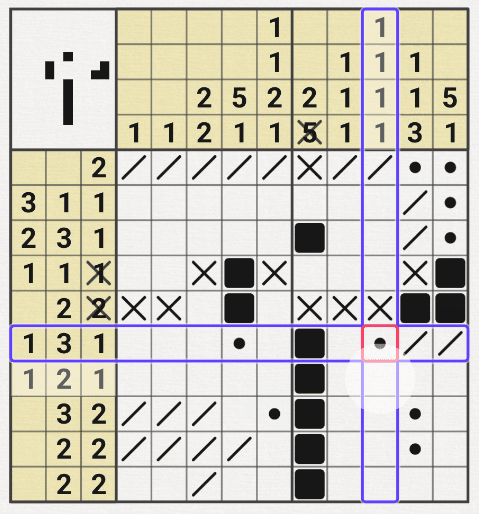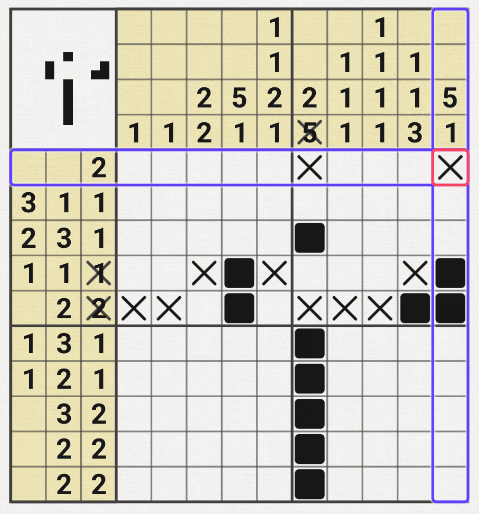
2번째는 잘 찍어서 그냥 판을 완료하는 럭키였다.

 

 

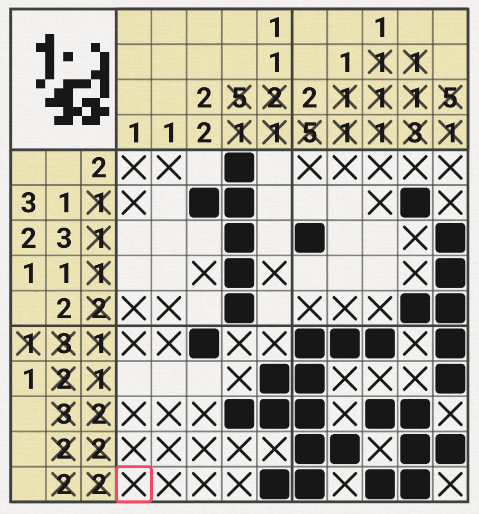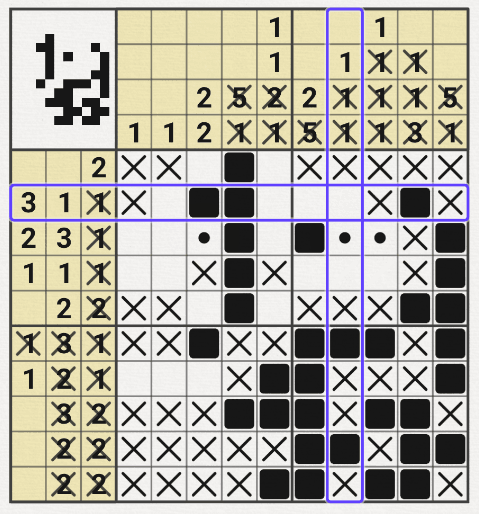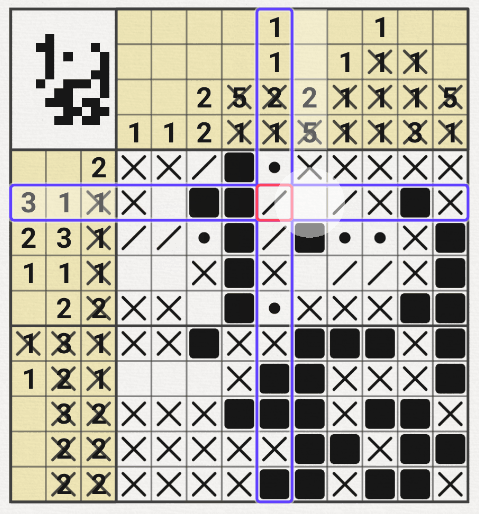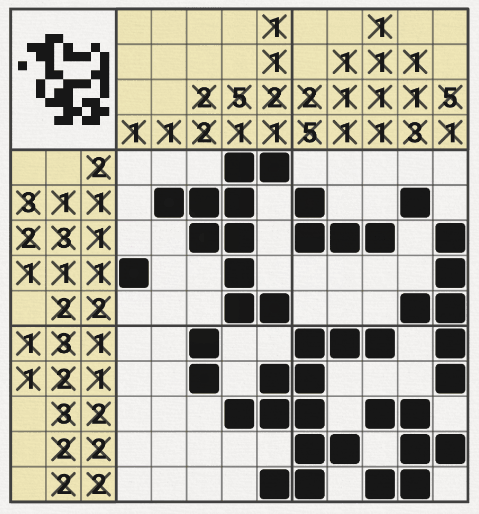
5월 21일 추가 > 30x30에서 막혀서 귀류법을 써봤다~

 

 

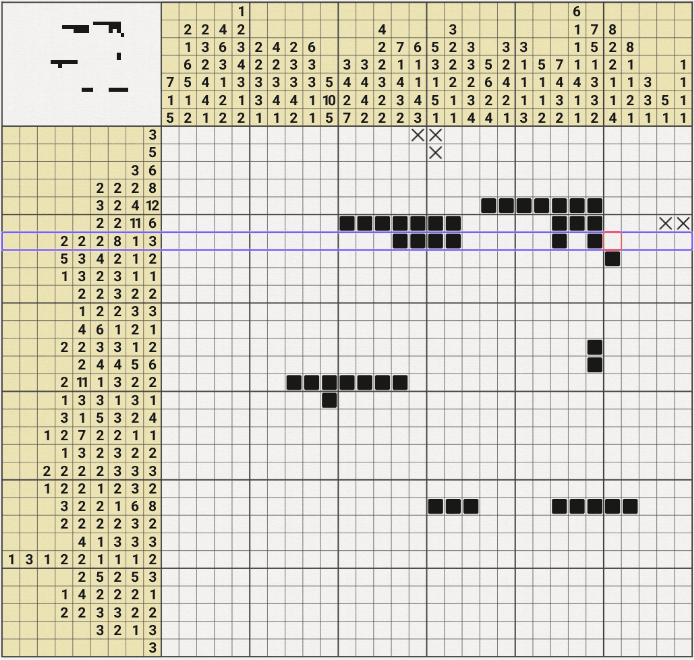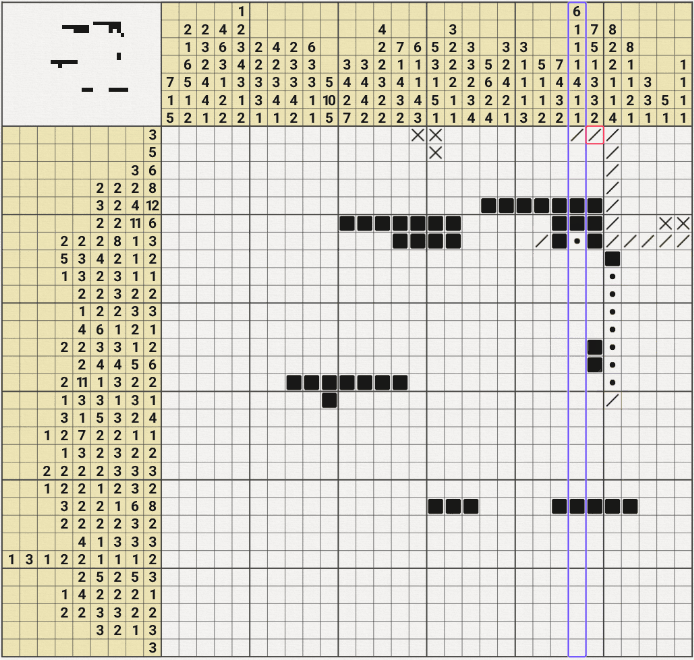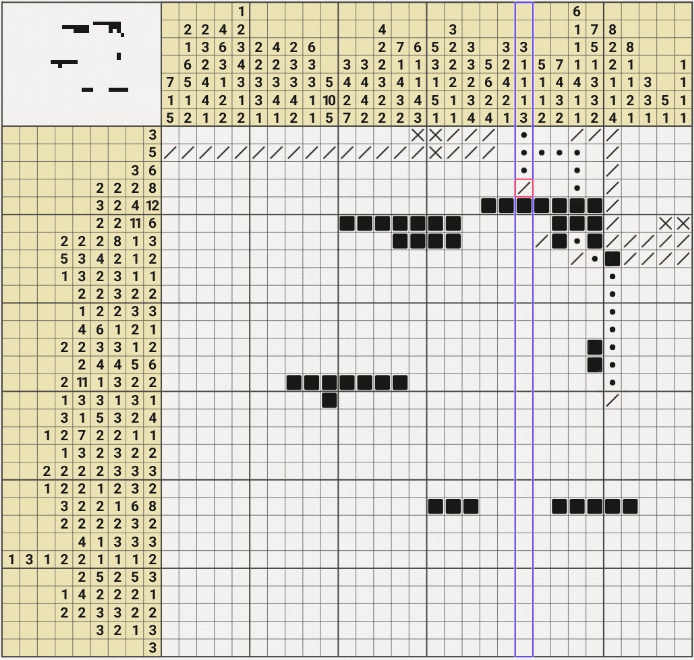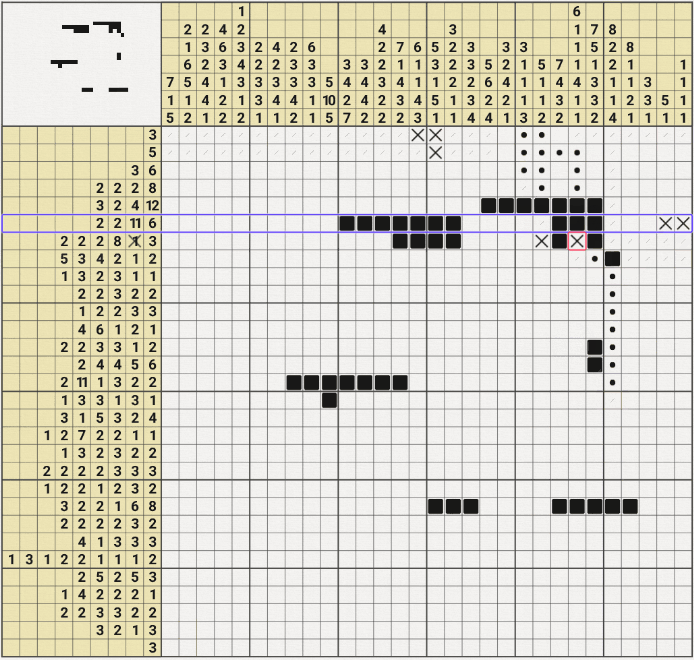
7행 24열을 참이라고 가정하고 진행해봤는데~

위의 움짤과 같이 6행의 2/2/11/6 중에서 6이 성립되지 않는 모순이 발생하여

7행 24열을 참이라는 가정이 성립되지 않아. X표시를 할 수 있었다.

 

 

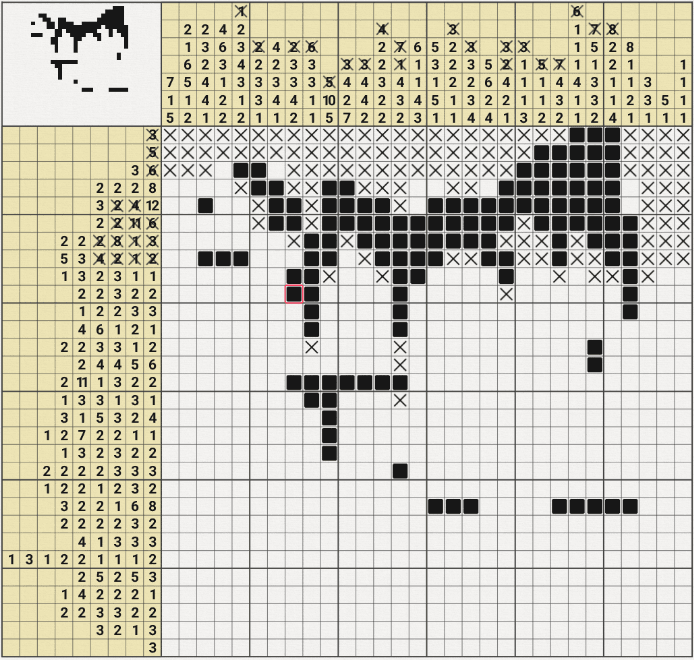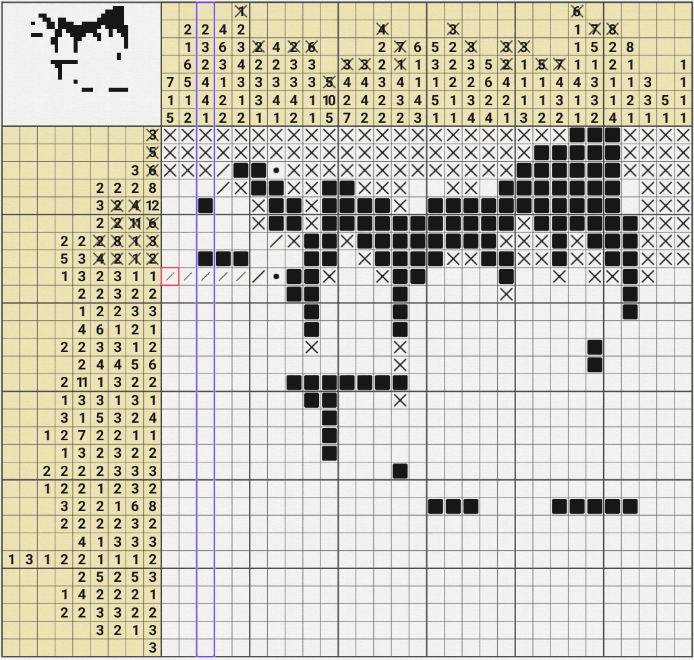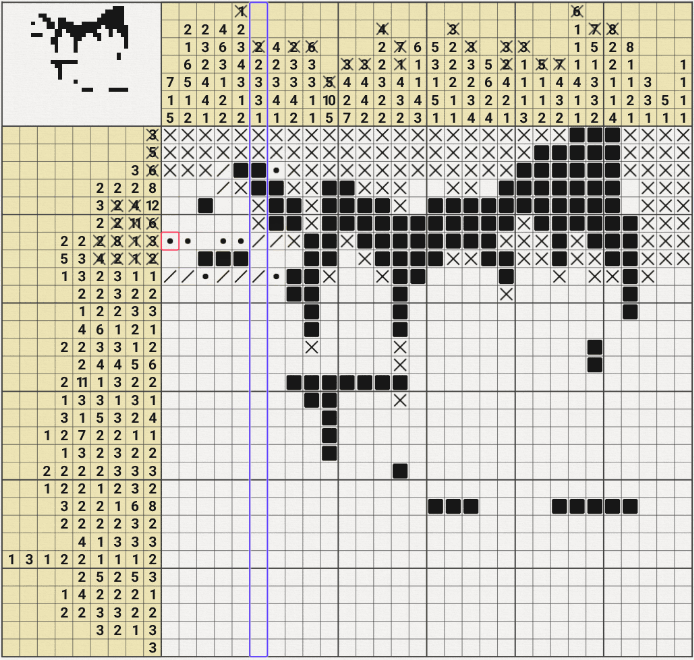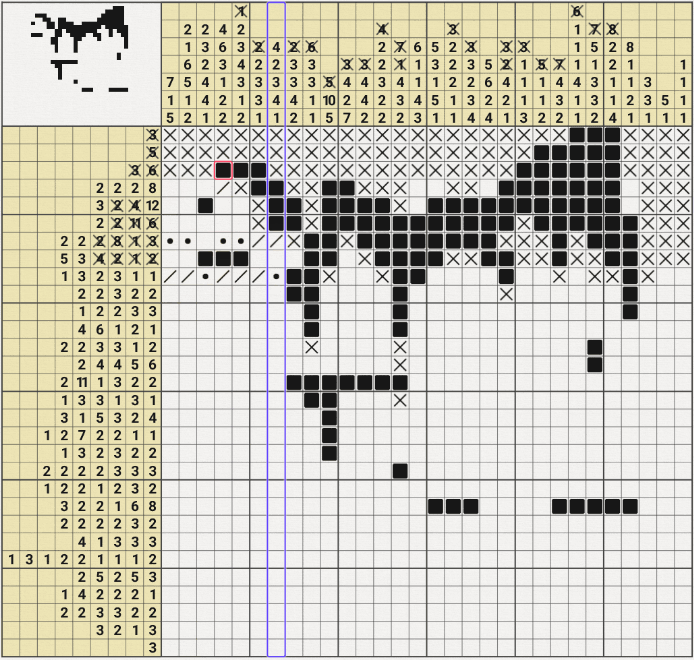
 같은 판에서 두 번째로 막혀서 위의 움짤과 같이

 3행 7열이 참이라는 가정으로 귀류법을 사용해봤는데

 1열의 7/1/5에서 7이 성립되지 않는 모순이 발생되어

 3행 7열이 참이라는 가정이 거짓이 되므로 X표시를 할 수 있었다.

 

5월 26일 추가 > 놀랍게도 5x5 판에도 숫자로만 풀리지 않는 판이 존재 했드아~~

아래는 컬러 노노그램인데 흑백보다 뭔가 답도 빨리 나오고 총 천연색이라 이뻐서 더 재미지다고 느껴지고 있다.